
Привет, Хабр! В этой статье я расскажу про создание математической модели длинного трубопровода для CAE-программы SimulationX на языке Modelica. Речь пойдёт о расчёте волновых процессов (пульсации давления, гидроудар и т.п.) в гидравлической линии методом характеристик. Несмотря на то, что этот метод довольно старый, в рунете довольно мало информации о его применении для решения прикладных задач.
Под катом я постараюсь объяснить зачем вообще нужно учитывать волновые процессы в трубопроводах, осветить проблемы, с которыми я столкнулся при программировании и в конце приведу сравнение процесса пульсаций давления при работе трёхплунжерного водяного насоса высокого давления на простой длинный трубопровод в модели и на стенде фирмы URACA в Германии.
Введение
В инженерной практике волновым процессам в трубопроводах, как правило, уделяют довольно мало внимания. Наиболее известный пример, когда волновые процессы портят жизнь инженеру, это гидроудар:
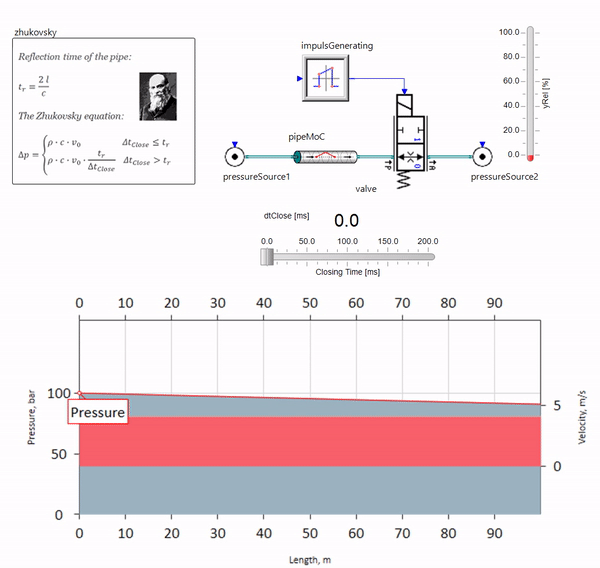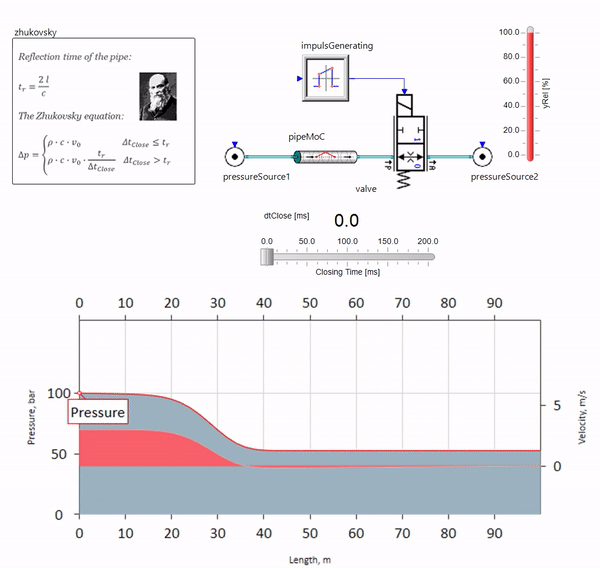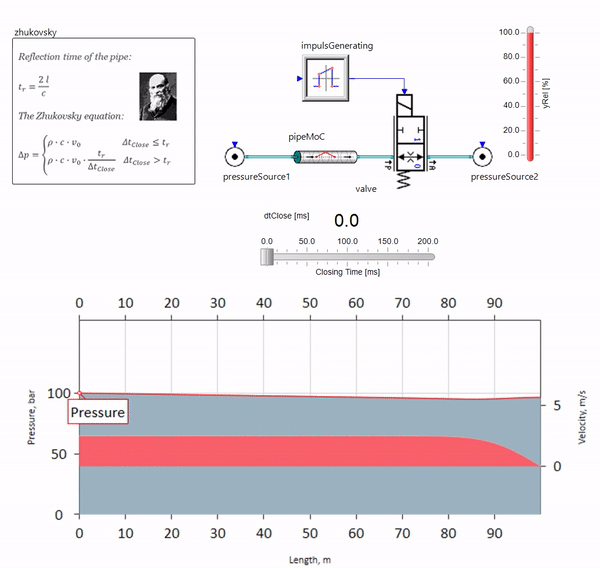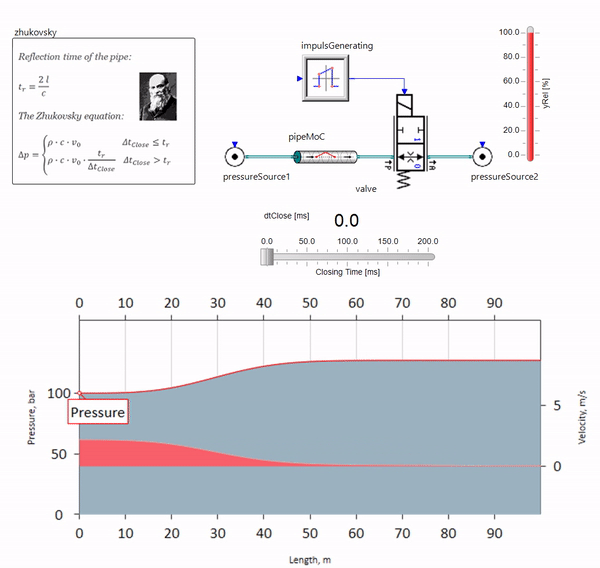
При быстром закрытии задвижки в конце трубопровода, находящемся внизу по течению, возникает волна давления, которая движется вверх по течению с местной скоростью звука (для воды — примерно 1500 м/с), отражается от источника постоянного давления, уходит обратно к задвижке и отражается от неё на этот раз с отрицательным знаком. Процесс этот повторяется до тех пор, пока вся энергия не израсходуется на трение, а до тех пор задвижка и весь трубопровод испытывают на себе ударные нагрузки, амплитуда и частота которых зависят от длины трубопровода и начальной скорости течения жидкости.
Гидроудар с необходимой для решения практических задач точностью описал в конце XIX века Николай Жуковский, решив таким образом проблему аварий на Московском водопроводе. С тех пор, формулу для расчёта скачка давления при быстром закрытии задвижки, во всём мире называют формулой Жуковского:
Гидроудар на практике проявляет себя, как правило, при длинах трубопровода от ста метров. При длинах ниже уже трудно найти гидравлическую аппаратуру, которая успела бы закрыться быстрее, чем волна давления пройдёт от задвижки и обратно (условие возникновения гидроудара). Тем не менее, даже относительно короткие трубопроводы всё ещё могут испортить жизнь инженерам, если в системе есть источник пульсаций расхода (например, объёмный насос с конечным числом плунжеров).
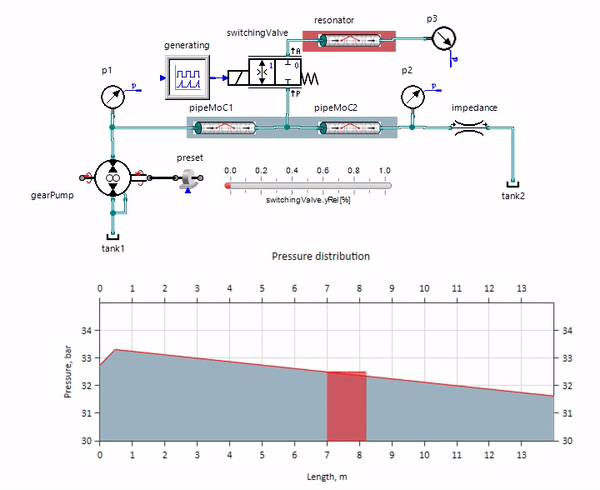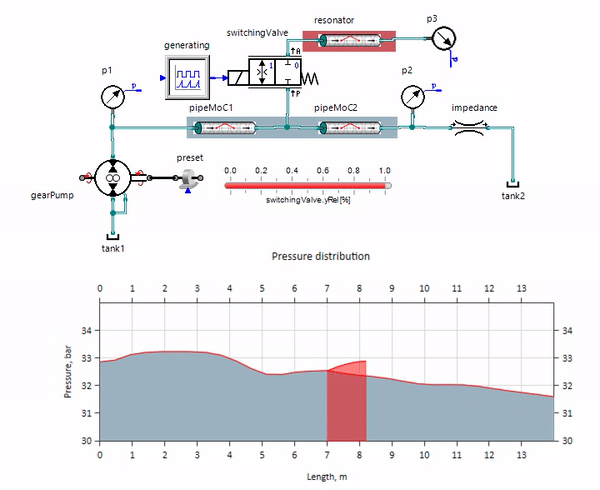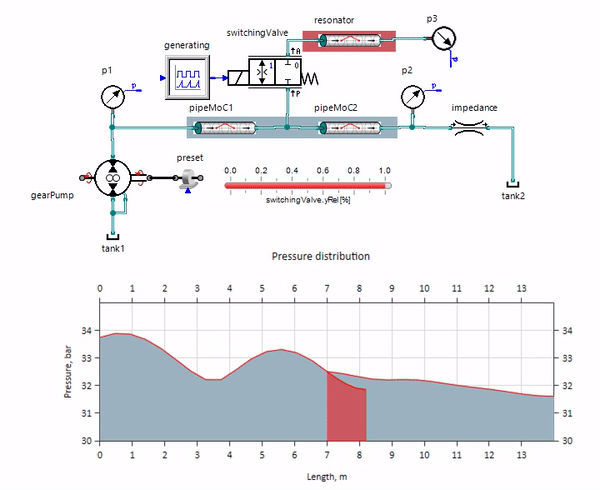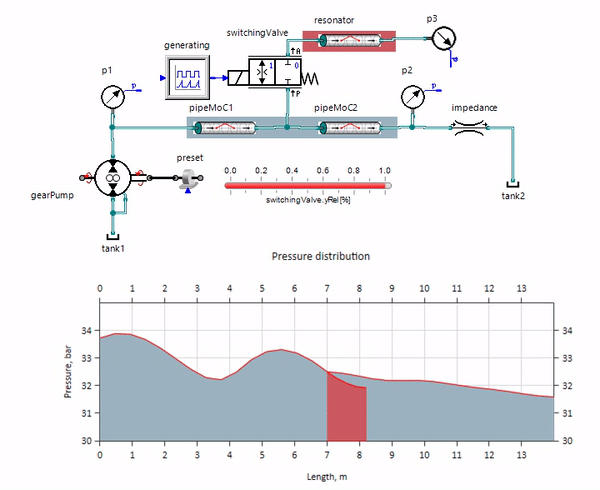
На гифке показано благотворное влияние кусочка трубопровода длиной всего чуть больше метра. Его длина равна четверти длины волны давления, поэтому при подключении его к основному трубопроводу, в нём возникает т.н. стоячая волна, которая в противофазе лупит по источнику пульсаций и подавляет их таким образом (это т.н. четвертьволновой гаситель пульсаций). Понятное дело, что при неудачном стечении обстоятельств эффект может быть и обратным.
В своей практике я долго пытался отмахиваться от волновых процессов, т.к. их расчёт требовал углубления в матан и численные методы, к которым на протяжении всей учёбы я относился со снисходительным пренебрежением. Но когда однажды я своими глазами увидел, что стандартные советы (поставить везде РВД, гидроаккумулятор, организовать подпор на всасе насоса) не помогают ни избавиться от пульсаций на стенде, ни, тем более, приближают к пониманию происходящих процессов, пришлось-таки углубляться в матан. Тем более к моему стыду, за меня уже начал писать модель трубопровода на С++ мой научный руководитель.
1. Одномерная модель гидравлической линии в распределённых параметрах
Основной проблемой, которая заставляет выходить из зоны комфорта традиционных одномерных моделей, описываемых обыкновенными дифференциальными уравнениями, это то, что самый простой трубопровод даже при самых зверских допущениях (полностью заполнен жидкостью, постоянное по длине поперечное сечение, скорость жидкости усредняется по сечению, процессы теплообмена не рассматриваются) описывается дифференциальными уравнениями в распределённых параметрах (уравнениями Эйлера, только с учётом массовой силы и трения в правой части второго уравнения):
где — плотность, — скорость, — давление, — потери на трение, — перепад давлений, вызванный гравитационной силой.
Т.е. интегрировать теперь нужно не только по времени , но и по пространственной координате .
В случае с жидкостями, можно ещё немного упростить себе жизнь, если переписать уравнения из консервативных переменных в примитивные переменные (скорость и давление):
где — скорость звука.
Теперь, если принять, что скорость звука существенно больше скорости движения жидкости (что справедливо при отсутствии кавитации), то уравнения станут ещё немного проще:
Чтобы решить эти уравнения, нужно тем или иным способом избавиться от дифференцирования по пространственной координате . В лоб это можно сделать, если заменить пространственный дифференциал конечно-разностной схемой, а в случае с временем тогда просто перейти к полному дифференциалу, сказав, что в рамках одной ячейки, параметры состояния не зависят от координаты:
Теперь эти уравнения можно решить как обыкновенные дифференциальные уравнения, разбив длину трубы на множество конечных объёмов. Так это и делается, например, в пакете Simscape, в MATLAB Simulink, так проблема решалась до недавнего времени в SimulationX.
Что-то таким образом, конечно, можно посчитать, но сильно мешают возникающие при этом численные колебания:
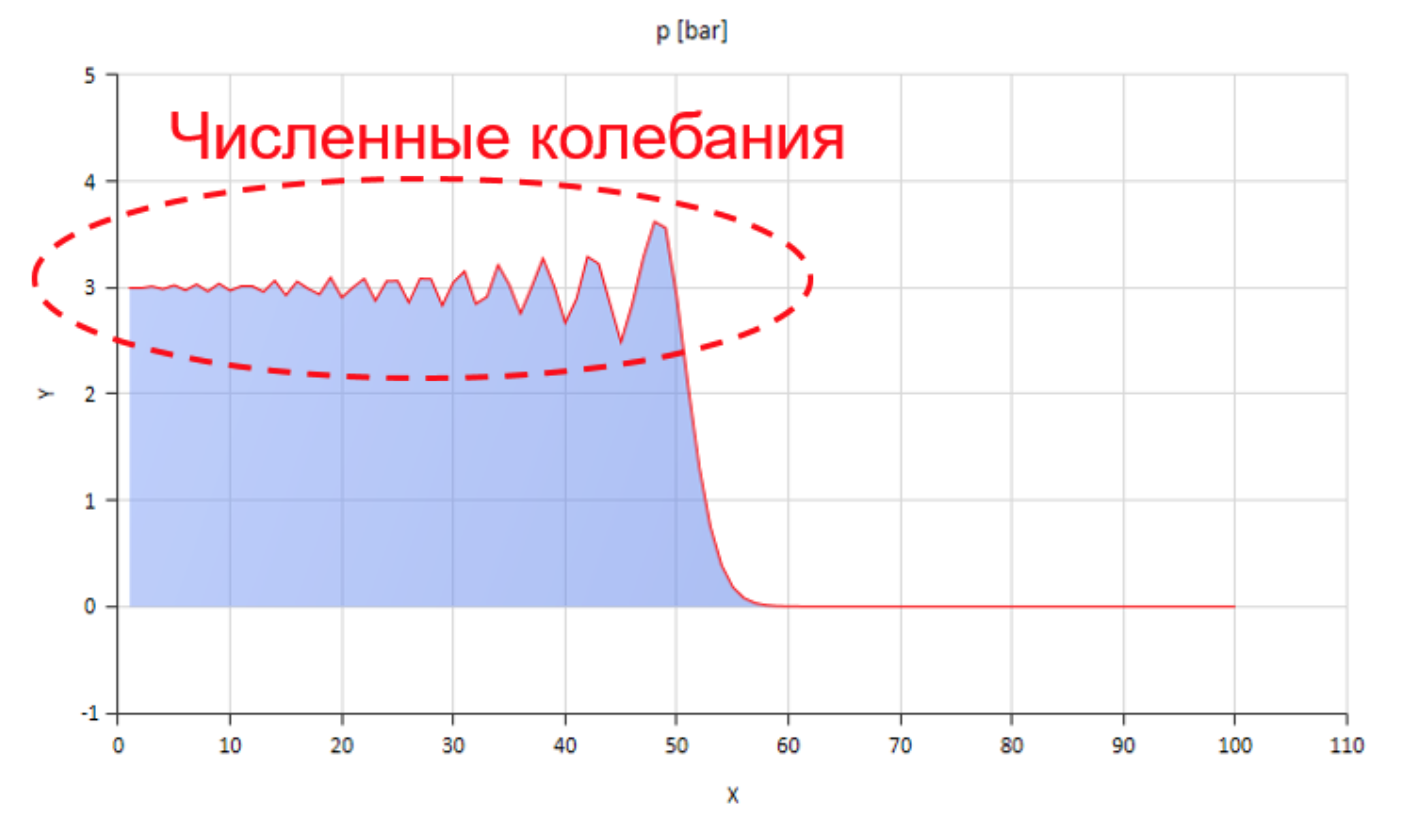
На рисунке изображён фронт волны давления, движущийся слева направо.
Можно бороться с этими колебаниями, например, вводя численную диффузию, но тогда существенно искажается скорость распространения волны. Можно увеличить трение (особенно помогает увеличение нестационарной её составляющей), но тогда модель перестаёт отражать физическую сущность.
Лучше всего использовать другой метод превращений уравнений в распределённых параметрах в обыкновенные дифференциальные уравнения, например — метод характеристик.
2. Метод характеристик
Википедия по запросу “Метод характеристик” рекомендует:
… отыскать такие характеристики, вдоль которых уравнение в частных производных превращается в обыкновенное дифференциальное уравнение. Как только найдены обыкновенные дифференциальные уравнения, их можно решить вдоль характеристик и найденное решение превратить в решение исходного уравнения в частных производных.Это как философский камень, только вместо превращения металлов в золото мы превращаем уравнения в частных производных в обыкновенные, и наоборот. Возникает вопрос: “как же применить это на практике?”, причём желательно более эффективно, чем это делали средневековые алхимики…
Для начала, разберёмся с постановкой задачи. В нашем распоряжении в начальный момент времени имеется какое-то распределение давлений и скоростей по длине трубы. Первым делом мы разобьём трубу на конечное число элементов и для каждой грани присвоим своё значение давления и скорости .
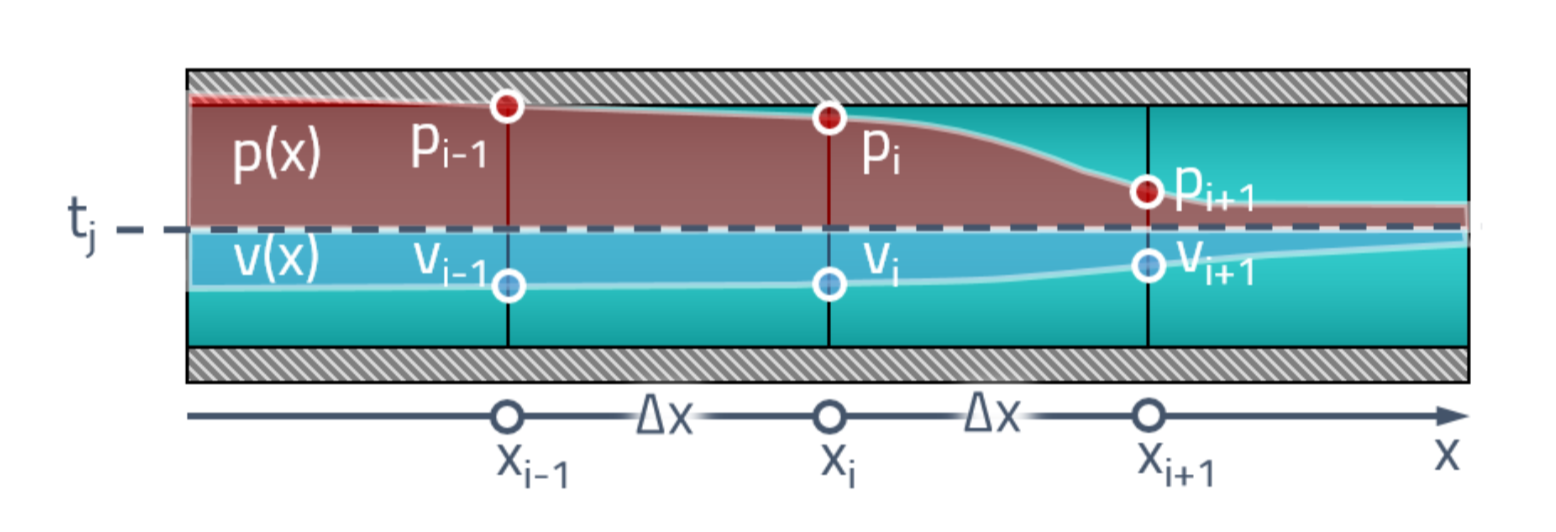
Интересует нас то, как изменятся значения в этих точках через момент времени . Перенесёмся в пространство-время и расположим состояние трубы в будущем выше начального состояния:

Вот здесь-то нам и пригодятся “магические” характеристики! Рабоче-крестьянское объяснение заключается в том, что все изменения в трубе происходят со скоростью звука. Давление и скорость в текущий момент времени в точке зависят от давления и скорости в тех точках трубы, где звуковая волна была (бы) секунд назад. Иллюстрируется это следующим образом:

Из какой-либо точки проводятся две симметричные линии, угол наклона которых определяется скоростью звука. Это и есть те самые характеристики, вдоль которых уравнения в частных производных превращаются в обыкновенные дифференциальные уравнения. Если мы назовём точки, в которых характеристики пересекаются с состоянием трубы в прошлом как и , уравнения запишутся следующим образом:
Значения давлений и скоростей в этих точках можно получить линейной интерполяцией между значениями параметров состояния на сетке:

Важно учитывать, что эти точки всегда должны находиться в пределах соседних ячеек! Для этого шаг времени должен удовлетворять критерию Куранта — Фридрихса — Леви (CFL):
Теперь к этим уравнениям можно применить хоть самую простую разностную схему:
В получившейся системе из двух уравнений две неизвестных: давление и скорость . Можно решать её численно, но нет особых проблем получить и аналитическое решение. Тогда, если принять постоянство скорости звука, получится полностью явная разностная схема.
Для закрепления приведу анимацию работы метода характеристик:
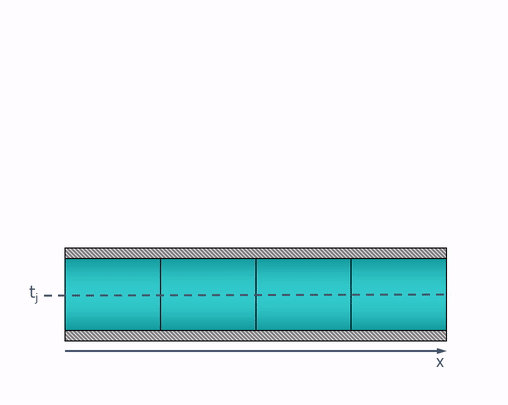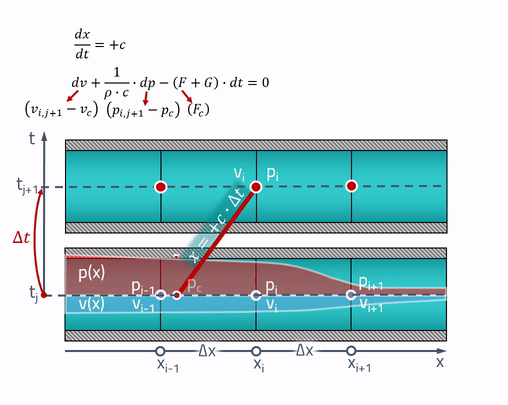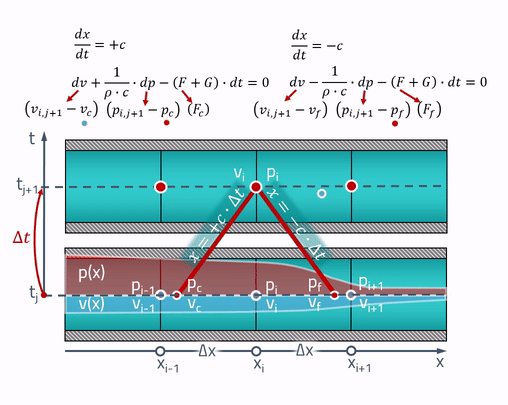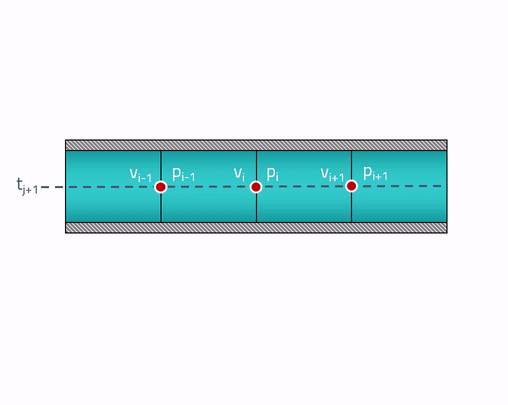
… скорость звука зависит от давления жидкости. В этом случае характеристики, строго говоря уже не будут прямыми линиями, а для того, чтобы найти давление, нужно уже будет знать скорость звука, которая от этого давления зависит. Т.е. схема будет уже неявной.
При создании модели, я принял допущение, что скорость звука слабо меняется от шага к шагу. Для жидкости это справедливо в случае низкого газосодержания и при отсутствии кавитации. Чтобы быть уверенным в результате, модель лучше использовать при давлениях от 10 бар.
3. Эксперимент
Мне представилась возможность окончательно довести до ума модель уже когда я начал работать в фирме ESI ITI GmbH в Дрездене. Как-то раз, я получил тикет в Helpdesk, где инженеры фирмы URACA жаловались, что не могут добиться сходимости с экспериментом с нашей “старой” трубой.
Они изготавливают водяные плунжерные насосы высокого давления, эдакие огромные “Керхеры” и хотели бы уметь предсказывать возможные резонансные эффекты, обусловленные в т.ч. волновыми процессами в трубопроводе. Проблема заключается в том, что у таких насосов, как правило, довольно мало плунжеров и работают они на низких оборотах (250-500 об/мин):

Из-за этого, а также из-за влияния сжимаемости жидкости, на выходе получается очень неравномерная подача:

Разрывы и нелинейности делают затруднительным процесс линеаризации и анализ модели в частотной области, а расчёты CFD для такой задачи — стрельба из пушки по воробьям. Кроме того, у них уже были модели в SimulationX, где они учитывали динамику механической части насоса, упругости рамы, характеристику электродвигателя, поэтому интересно было бы посмотреть как на это повлияет трубопровод.
Схема испытательного стенда довольно простая:
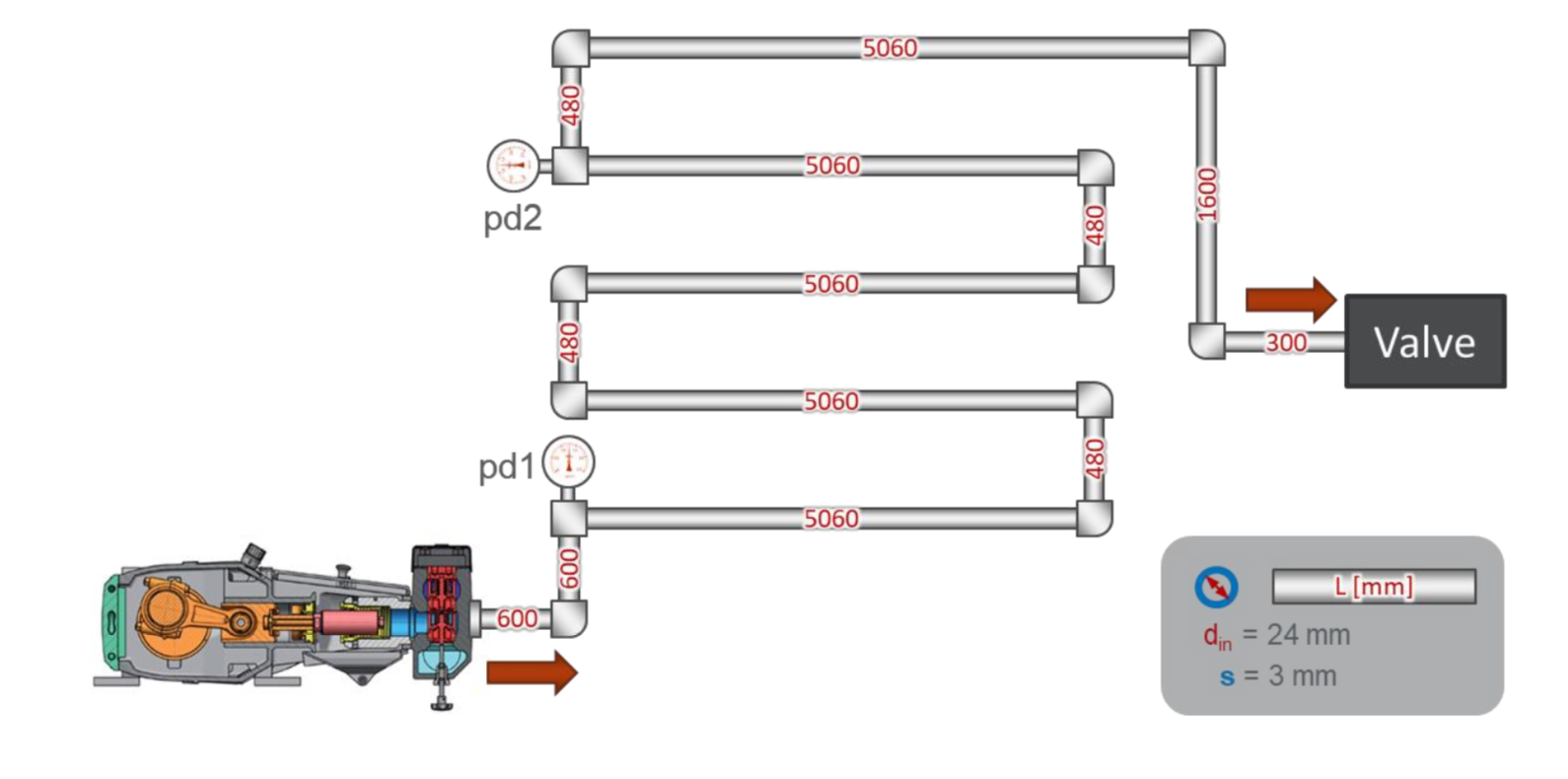
Имеется простой трубопровод общей длиной примерно 30 метров. В начале трубопровода установлен датчик давления pd1, на расстоянии 22 метра от него — датчик давления pd2. В конце трубопровода клапан, которым настраивается давление в системе.
Я предложил протестировать бета-версию своей модели, в результате в SimulationX была собрана такая модель:
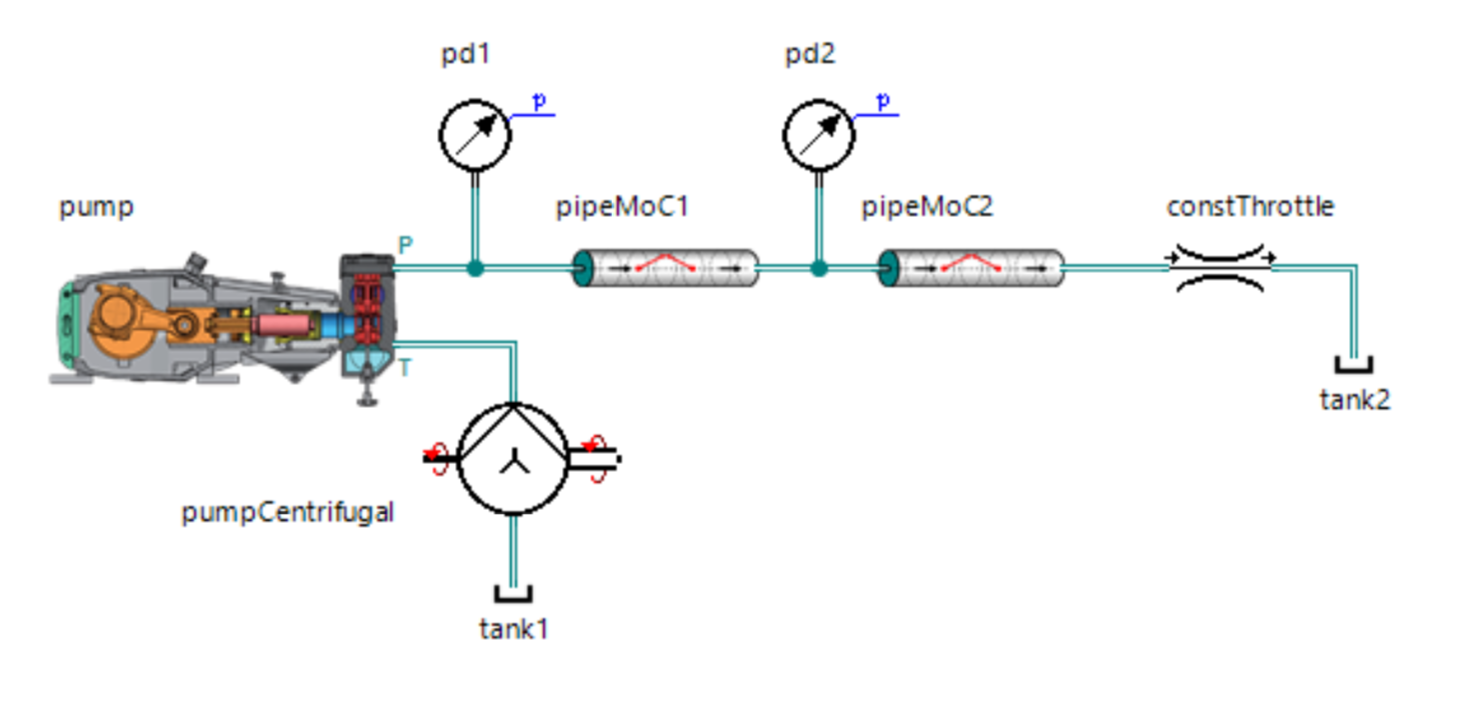
Результаты даже меня приятно удивили:
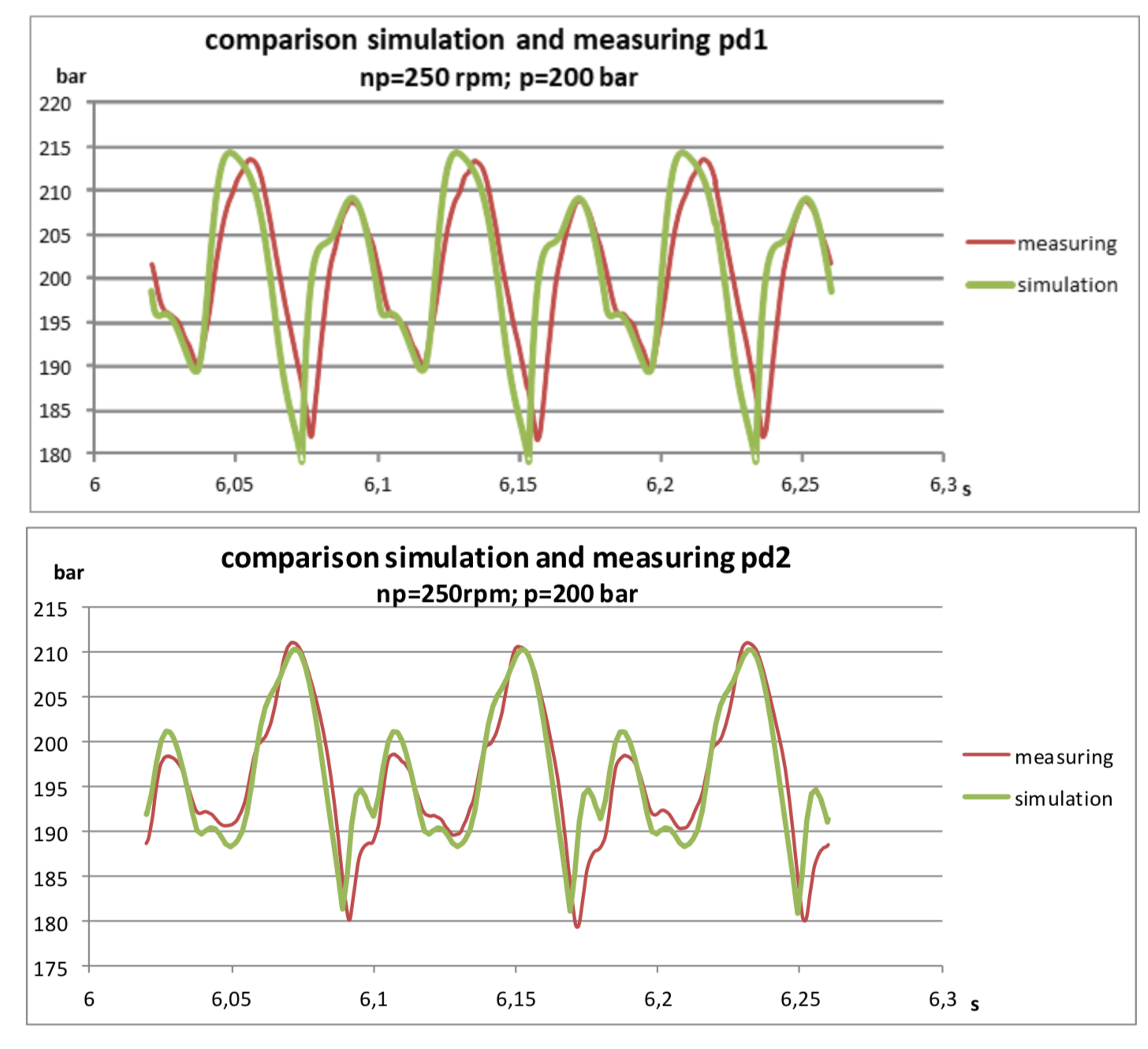
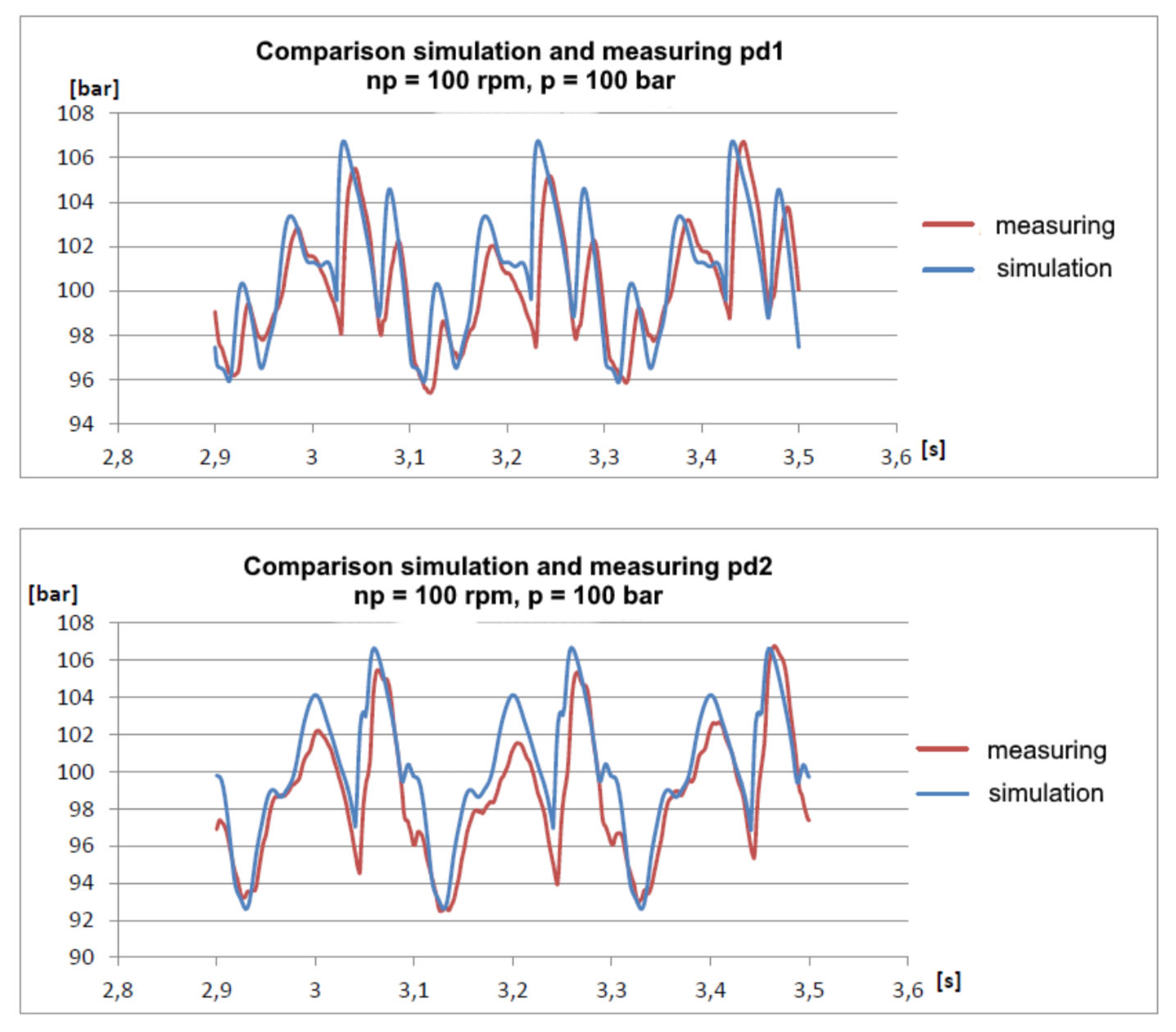
Видно, что модель немного хуже задемпфирована, что и понятно при условии, что в ней никак не учитывались гидравлические сопротивления. Тем не менее, основные гармоники довольно хорошо совпадают и позволяют с довольно хорошей точностью предсказывать значения амплитуд давления.
Этот опыт позволил оперативно запустить в релиз SimulationX новую модель гидравлической линии, а я погрузился в эту тему и не заметил как вместе со студентом-практикантом запилил и модель пневматической линии, где всё было гораздо интереснее. Там пришлось использовать метод на основе метода Годунова, который в свою очередь базируется на решении задачи Римана о распаде произвольного разрыва, ну да об этом уже как-нибудь в другой раз…
Литература
- В отечественной литературе метод характеристик для инженерного применения лучше всего описан в книге «Гидромеханика», Д. Н. Попов, С. С. Панаиотти, М.В. Рябинин.
- В своей публикации Pipeline simulation by the method of characteristics for calculating the pressure pulsation of a high-pressure water plunger pumpя более подробно рассмотрел проблемы стыковки метода характеристик и решателя ОДУ.«Dr.-Ing.(Rus) Maxim Andreev, Dipl.-Ing. Uwe Gratz and Dipl.-Ing. (FH) Achim Lamparter», The 11th International Fluid Power Conference, 11. IFK, March 19-21, 2018, Aachen, Germany, за текстом обращайтесь в личку
- У кого есть доступ к немецким библиотекам, лучший обзор методов решения гиперболических уравнений в применении к гидравлическим линиям, который я встречал, содержится в следующей диссертации: Beck, M., Modellierung und Simulation der Wellenbewegung in kavitierenden Hydraulikleitungen, Univ. Stuttgart, Germany, 2003.
- Классика жанра по гиперболическим уравнениям в целом: Randall J. Leveque, Finite Volume Methods for Hyperbolic Problems, Cambridge University Press, Cambridge, United Kingdom, 2002.
Комментарии (15)

ChePeter
29.07.2018 15:42В Москве Ликсутов декларировал управление движением автотранспорта с помощью гидродинамики.
Ты бы им подсказал бы что ли что нибудь толковое, а мы бы поддержали.
PDF файл обзора с его предисловием вот тут
www.mou.mipt.ru/gasnikov1129.pdf&sa=U&ved=0ahUKEwjju5KIqcTcAhUBJJoKHUbgCAgQFggLMAA&usg=AOvVaw0yMhdT-LFup7UUW78_wGGw
Maxim_Andreev Автор
29.07.2018 15:52Ссылка битая.
К гидродинамике эта задача имеет лишь посредственное отношение. Транспортный поток тоже можно описать гиперболическими уравнениями, например, уравнением переноса (адвекции). Если учитывать зависимость скорости движения от плотности потока, уравнение уже становится нелинейным. Там тоже, как и в случае с пневматической трубой нужно использовать решатели на основе метода Годунова.
Решение таких уравнений детально разобрано в книге 4 из моего списка литературы. Ключевые слова — traffic flow, nonlinear scalar conservation laws. Уверен, что уже есть софт для решения таких проблем.

maisvendoo
29.07.2018 20:22Применимы ли приведенные алгоритмы для расчета процессов в тормозной магистрали поезда?

Maxim_Andreev Автор
29.07.2018 21:34Скорее всего, речь о пневматической линии? Если так, то сами уравнения, которые здесь рассматриваются, справедливы только при акустических допущениях (волна давления настолько мала, что скорость звука можно считать постоянной). В тормозной магистрали речь может идти о скачках давления до 10 бар, и метод характеристик в этом случае начнёт сбоить и выдавать нефизичный результат.
Сейчас в SimulationX пневматические тормозные системы поездов и автомобилей считаются с моделью трубы методом конечных объёмов с примитивной схемой дискретизации первого порядка, но решаются при этом уравнения Эйлера с учётом теплообмена, а не уравнения акустики. Проблема численных колебаний тоже возникает (особенно нефизично себя ведёт распределение температуры), но задержка сигнала, вызванная конечной скоростью прохождения волны, моделируется довольно точно (Daimler Trucks довольны).
Сейчас у меня в стадии бета-теста модель пневматической линии, которая может считать в т.ч. ударные волны, она должна быть лишена и этих недостатков.

kiralexx
30.07.2018 12:19Да, соглашусь метод характеристик довольно стар и, возможно, (поправьте меня, если это не так) не самым лучшим образом подходит для решения задач с разрывами.
Не пробовали использовать WENO-схемы для дискретизации по пространству и TVD Runge-Kutta для дискретизации по времени?
Насколько мне известно, на данный момент одни из лучших схем для решения гиперболических систем уравнений методами конечного объема и конечных разностей, так как обеспечивают высокий порядок точности в областях непрерывного изменения параметров как по пространству, так и по времени, а также не вызывают видимых осцилляций (не зря они называются Essentially Non-Oscillatory) и не сильно размывают ударные волны и контактные разрывы.
Они требуют достаточно много вычислений на одну ячейку (точку), но это не то, о чем стоит заботиться при одномерных расчетах.
Maxim_Andreev Автор
30.07.2018 12:39Конечно, разрывы считаются только решателями на основе метода Годунова.
До WENO и TVD я пока не дошёл, для модели пневматической линии остановился пока на HLLE. Он хорош тем, что не нужно бояться проблем с энтропией на разрывах, но, действительно, фронт волны замазывает довольно сильно. Нужно будет протестировать на реальной системе, но я подозреваю, что для практического применения в том же пневмоприводе, HLLE хватит с запасом.
По поводу трудоёмкости вычислений, к сожалению, уже и с HLLE приходится беспокоиться о производительности, т.к. вычисление параметров состояния из-за особенностей Modelica требует итераций внутри каждого шага, трение, массовые силы и обмен количеством теплоты приходится считать методом предиктор-корректор, а для того, чтобы подружить трубу с другими элементами библиотеки, нужно считать скоростной напор на границах трубы тоже по неявной схеме… В итоге даже одномерная труба на 30-40 ячеек уже довольно сильно грузит модель. Особенно неприятно, что труба не даёт увеличить шаг основному решателю ОДУ, даже если в ней ничего не происходит.
В общем, если бы я делал это для диссертации, конечно же слепил бы на коленке TVD, но для софта приходится много думать об юзабилити…

Maxim_Andreev Автор
30.07.2018 13:09Что же касается гидравлических линий, то там проблемы разрывов не так актуальны. Продвинутый решатель может пригодиться для расчётов в кавитирующей всасывающей линии (т.к. скорость звука в двухфазной среде масло-воздух может быть сопоставима со скоростями движения жидкости), но в Германии на этот счёт нет единого мнения. В Штуттгарте для таких задач использовали MUSCL (диссертация Roman Etlender), в Дрездене сочли, что в таких задачах нужно уходить в полноценную CFD (исследование ТУ Дрездена по VDMA), в Аахене в программе DSH+ модифицировали метод характеристик, который тоже даёт неплохую сходимость с экспериментом.

petuhoff
01.08.2018 00:42А можно ли получить модель этой трубы и график изменения давления на границах, что бы сравнить с нашей моделью. Мы на 100 км тестировали с упругими стенками и получалось не плохо:
 "
"
Maxim_Andreev Автор
01.08.2018 10:20В пробной профессиональной версии с сайта есть эта модель.
На ваших графиках как раз видны численные колебания на фронте волны. Но в данном случае, когда фронт растянут на километры, с этими колебаниями, конечно можно жить.


vassabi
теперь вам надо пойти в университет научным руководителем и обучить студента — чтобы вернуть долг альма-матер :)
Maxim_Andreev Автор
Так я работал в университете в общей сложности около 6 лет, из них около трёх — преподавателем. Все «долги» давно вернул)
petuhoff
Уже за то, что текст на русском можно сказать спасибо.
Тем кому интересна тема оценят и без университета.