Привет, Хабр! Представляю вашему вниманию перевд статьи Solving multiarmed bandits: A comparison of epsilon-greedy and Thompson sampling.

Задача о многоруком бандите

Задача о многоруком бандите – одна из самых основных задач в науке о решениях. А именно, это задача об оптимальном распределении ресурсов в уcловиях неопределенности. Само название «многорукий бандит» пошло от старых игровых автоматов, которыми управляли при помощи ручек. Эти автоматы получили прозвище «бандиты», потому что после общения с ними люди обычно чувствовали себя ограбленными. А теперь представьте, что таких машин несколько и шанс выиграть у разных машин разный. Раз уж мы взялись играть с этими машинами, мы хотим определить, у какой этот шанс выше и использовать (exploit) эту машину чаще, чем другие.

Проблема в следующем: как нам эффективнее всего понять, какая машина подходит лучше всего, и при этом перепробовать много возможностей в реальном времени? Это не какая-то теоретическая проблема, это проблема, с которой бизнес сталкивается все время. Например, у компании есть несколько вариантов сообщений, которые надо показывать пользователям (в число сообщений, например, входят и реклама, сайты, изображения) так, чтобы выбранные сообщения максимизировали некое бизнес-задание (конверсию, кликабельность и пр.)

Типичный способ решить эту задачу – много раз запускать A/B тесты. Т.е сколько-то недель показывать каждый из вариантов одинаково часто, а потом, исходя из статистических тестов, решить, какой вариант лучше. Такой способ подойдет, когда вариантов немного, скажем, 2 или 4. Но когда вариантов много, такой подход становится неэффективным – и по упущенному времени, и по упущенной выгоде.

Откуда появляется упущенное время, должно быть легко понятно. Больше вариантов – надо больше A/B тестов – надо больше времени на принятие решения. Возникновение упущенной выгоды не так очевидно. Упущенная выгода (opportunity cost) – издержки, связанные с тем, что вместо одного действия мы совершили другое, то есть, говоря упрощенно, это то, что мы потеряли, вложившись в A вместо B. Вложение в B – и есть упущенная выгода от вложения в A. То же и с проверкой вариантов. A/B тесты не должны прерываться, пока они не закончились. Это значит, что экспериментатор не знает, какой вариант лучше, пока тестирование не закончилось. Однако, все же предполагается, что один вариант будет лучше, чем другие. Это значит, что, продлевая A/B тесты, мы показываем не самые лучшие варианты достаточно большому числу посетителей (хоть и не знаем, какие именно варианты не самые лучшие), упуская тем самым свою прибыль. Это и есть упущенная выгода от A/B тестирования. Если A/B тест только один, то, возможно, упущенная выгода совсем не велика. Большое число А/В тестов означает, что мы должны длительное время показывать клиентам множество не самых лучших вариантов. Было бы лучше, если бы можно было быстро в реальном времени откинуть плохие варианты, а уже потом, когда вариантов останется мало, использовать для них A/B тесты.

Сэмплеры или агенты – это способы быстро тестировать и оптимизировать распределение вариантов. В этой статье я познакомлю вас с Топмсоновским сэмплированием (Thompson sampling) и его свойствами. Я также сравню томпсоновское сэмплирование с эпсилон-жадным алгоритмом — другим популярным вариантом для задачи о многоруком бандите. Все будет реализовано на Python с чистого листа – весь код можно найти здесь.

Краткий словарь понятий

• Агент, сэпмлер, бандит (agent,sampler, bandit) – алгоритм, который делает решения касательно того, какой вариант показывать.
• Вариант (variant) – разный вариант сообщения, которое видит посетитель.
• Действие (action) – действие, которое выбрал алгоритм (какой вариант показывать).
• Использовать (exploit) – делать выбор с целью максимизировать суммарную награду исходя из имеющихся данных.
• Исследовать, пробовать (explore) – делать выбор с целью лучше понять окупаемость для каждого варианта.
• Награда, очки (score,reward) – бизнес-задание, например, конверсия или кликабельность. Для простоты считаем, что она распределена биномиально и равна либо 1, либо 0 — кликнули или нет.
• Окружающая среда – контекст, в котором агент работает – варианты и их скрытая для пользователя “окупаемость”.
• Окупаемость, вероятность успеха (payout rate) – скрытая переменная, равная вероятности получить score=1, для каждого варианта она своя. Но пользовтаель ее не видит.
• Попытка (trial) – пользователь заходит на страницу.
• Сожаление (regret) – это разница между тем, какой был бы самый лучший результат из всех доступных вариантов и какой был результат из варианта, доступного на текущей попытке. Чем меньше сожаление по отношению к уже сделанным действиям, тем лучше.
• Сообщение (message) – баннер, вариант страницы и прочее, разные варианты которого мы хотим попробовать.
• Сэмплирование (sampling) – генерация некой выборки из заданного распределения.

Исследовать и использовать (Explore and exploit)

Агенты – алгоритмы, которые ищут подход к выбору решений в реальном времени, чтобы достичь баланс между исследованием пространства вариантов и использованием самого оптимального варианта. Этот баланс очень важен. Пространство вариантов надо исследовать, чтобы иметь понятие о том, какой вариант самый лучший. Если мы сначала обнаружили этот самый оптимальный вариант, а потом все время его используем – мы максимизируем суммарную награду, которая нам доступна из окружающей среды. С другой стороны, мы также хотим исследовать другие возможные варианты – вдруг они в будущем окажутся лучше, а мы просто этого пока не знаем? Иными словами, мы хотим застраховаться против возможных убытков, пробуя немного экспериментировать с субоптимальными вариантами, чтобы уточнить для себя их окупаемость. Если их окупаемость на самом деле более высокая, их можно показывать чаще. Другой плюс от исследования вариантов в том, что мы можем лучше понять не только среднюю окупаемость, но и то, как примерно окупаемость распределяется, т.е мы можем лучше оценить неопределенность.
Главная проблема, следовательно, это решить – как лучше всего выйти из дилеммы между исследованием и использованием (exploration-exploitation tradeoff).

Эпсилон-жадный алгоритм (epsilon-greedy algorithm)

Типичный способ выйти из этой дилеммы– эпсилон-жадный алгоритм. «Жадный» означает именно то, о чем вы подумали. После некого начального периода, когда мы случайно делаем попытки – скажем, 1000 раз, алгоритм жадно выбирает самый лучший вариант k в e процентах попыток. Например, если e=0.05, алгоритм 95% времени выбирает лучший вариант, а в оставшиеся 5% времени выбирает случайные попытки. На самом деле, это довольно эффективный алгоритм, однако он может недостаточно исследовать пространство вариантов, и следовательно, недостаточно хорошо оценить, какой вариант самый лучший, застрять на субоптимальном варианте. Давайте покажем в коде, как этот алгоритм работает.

Но сначала некоторые зависимости. Мы должны определить окружающую среду Environment. Это контекст, в котором алгоритмы будут запускаться. В данном случае, контекст очень простой. Он вызывает агента, чтобы агент решил, какое выбрать действие, дальше контекст запускает это действие и возвращает полученные за него очки обратно агенту (который как-то обновляет свое состояние).

class Environment:
	    def __init__(self, variants, payouts, n_trials, variance=False):
	        self.variants = variants
	        if variance:
	            self.payouts = np.clip(payouts + np.random.normal(0, 0.04, size=len(variants)), 0, .2)
	        else:
	            self.payouts = payouts
	        #self.payouts[5] = self.payouts[5] if i < n_trials/2 else 0.1
	        self.n_trials = n_trials
	        self.total_reward = 0
	        self.n_k = len(variants)
	        self.shape = (self.n_k, n_trials)
	        
	    def run(self, agent):
	        """Run the simulation with the agent. 
	        agent must be a class with choose_k and update methods."""
	        
	        for i in range(self.n_trials):
	            # agent makes a choice
	            x_chosen = agent.choose_k()
	            # Environment returns reward
	            reward = np.random.binomial(1, p=self.payouts[x_chosen])
	            # agent learns of reward
	            agent.reward = reward
	            # agent updates parameters based on the data
	            agent.update()
	            self.total_reward += reward
	        
	        agent.collect_data()
	        
	        return self.total_reward

Очки распределены биномиально с вероятностью p, зависящей от номера действия (точно также они могли бы быть распределены и непрерывно, суть бы не поменялась). Также я определю класс BaseSampler – он нужен просто чтобы хранить логи и различные атрибуты.

class BaseSampler:	    
	    def __init__(self, env, n_samples=None, n_learning=None, e=0.05):
	        self.env = env
	        self.shape = (env.n_k, n_samples)
	        self.variants = env.variants
	        self.n_trials = env.n_trials
	        self.payouts = env.payouts
	        self.ad_i = np.zeros(env.n_trials)
	        self.r_i = np.zeros(env.n_trials)
	        self.thetas = np.zeros(self.n_trials)
	        self.regret_i = np.zeros(env.n_trials)
	        self.thetaregret = np.zeros(self.n_trials)
	        
	        self.a = np.ones(env.n_k) 
	        self.b = np.ones(env.n_k) 
	        self.theta = np.zeros(env.n_k)
	        self.data = None
	        self.reward = 0
	        self.total_reward = 0
	        self.k = 0
	        self.i = 0
	        
	        self.n_samples = n_samples
	        self.n_learning = n_learning
	        self.e = e
	        self.ep = np.random.uniform(0, 1, size=env.n_trials)
	        self.exploit = (1 - e)
	        
	    def collect_data(self):
	        
	        self.data = pd.DataFrame(dict(ad=self.ad_i, reward=self.r_i, regret=self.regret_i))

Ниже определим 10 вариантов и окупаемость для каждого. Самый лучший вариант – вариант 9 с окупаемостью 0.11%.

variants = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
payouts = [0.023, 0.03, 0.029, 0.001, 0.05, 0.06, 0.0234, 0.035, 0.01, 0.11]

Чтобы было от чего отталкиваться, также определим класс RandomSampler. Этот класс нужен в качестве baseline модели. Он просто чисто случайно выбирает вариант на каждой попытке и не обновляет свои параметры.

class RandomSampler(BaseSampler):
	    def __init__(self, env):
	        super().__init__(env)
	        
	    def choose_k(self):
	        
	        self.k = np.random.choice(self.variants)
	        
	        return self.k
	    
	    def update(self):
	        # nothing to update
	        #self.thetaregret[self.i] = self.thetaregret[self.i]
	        #self.regret_i[self.i] = np.max(self.thetaregret) - self.theta[self.k]
	        #self.thetas[self.i] = self.theta[self.k]
	        self.thetaregret[self.i] = np.max(self.theta) - self.theta[self.k]
	        
	        self.a[self.k] += self.reward
	        self.b[self.k] += 1
	        self.theta = self.a/self.b
	
	        self.ad_i[self.i] = self.k
	        self.r_i[self.i] = self.reward
	        self.i += 1

У остальных моделей структура следующая. У всех есть методы choose_k и update. choose_k реализует метод, с использованием которого агент выбирает вариант. update обновляет параметры агента – этот метод характеризует, как меняется возможность агента выбрать вариант (у RandomSampler эта возможность никак не меняется). Мы запускаем агента в окружающей среде используя следующий паттерн.

en0 = Environment(machines, payouts, n_trials=10000)
rs = RandomSampler(env=en0)
en0.run(agent=rs)

Суть эпсилон-жадного алгоритма такова.

1. Случайным образом выбрать k для n попыток.
2. На каждой попытке для каждого варианта оценить выигрыш.
3. После всех n попыток:
4. С вероятностью 1-e выбрать k с самым высоким выигрышем;
5. С вероятностью e выбрать K случайно.

Код эпсилон-жадного алгоритма:

class eGreedy(BaseSampler):
	
	    def __init__(self, env, n_learning, e):
	        super().__init__(env, n_learning, e)
	        
	    def choose_k(self):
	
	        # e% of the time take a random draw from machines
	        # random k for n learning trials, then the machine with highest theta
	        self.k = np.random.choice(self.variants) if self.i < self.n_learning else np.argmax(self.theta)
	        # with 1 - e probability take a random sample (explore) otherwise exploit
	        self.k = np.random.choice(self.variants) if self.ep[self.i] > self.exploit else self.k
	        return self.k
	        # every 100 trials update the successes
	
	        # update the count of successes for the chosen machine
	    def update(self):
	        
	        # update the probability of payout for each machine
	        self.a[self.k] += self.reward
	        self.b[self.k] += 1
	        self.theta = self.a/self.b
	
	        #self.total_reward += self.reward
	        #self.regret_i[self.i] = np.max(self.theta) - self.theta[self.k]
	        #self.thetaregret[self.i] = self.thetaregret[self.i]
	        self.thetas[self.i] = self.theta[self.k]
	        self.thetaregret[self.i] = np.max(self.thetas) - self.theta[self.k]
	 
	        self.ad_i[self.i] = self.k
	        self.r_i[self.i] = self.reward
	        self.i += 1

Ниже на графике вы можете видеть результаты чисто рандомного сэмплирования, то есть, другими словами, здесь нет никакой модели. На графике показано, какой выбор алгоритм делал на каждой попытке, если попыток было 10 тысяч. Алгоритм только пробует, но не учится. Всего он набрал 418 очков.

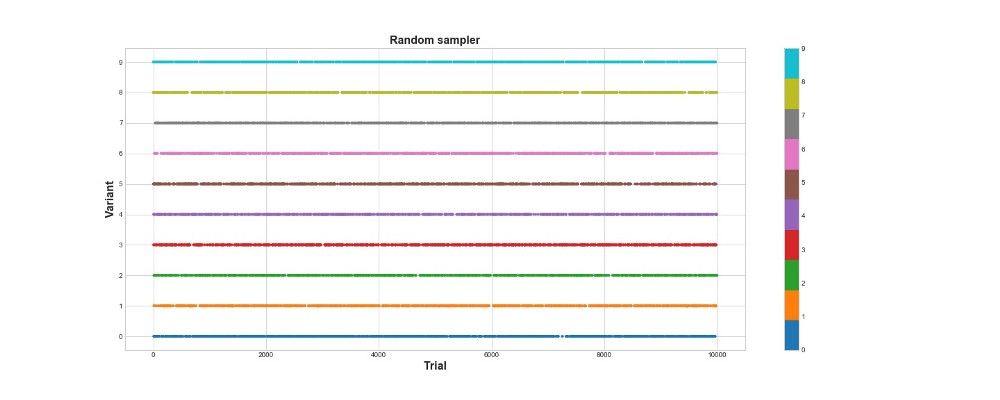
Давайте посмотрим, как ведет себя в той же окружающей среде эпсилон-жадный алгоритм. Запустим алгоритм на 10 тысяч попыток с e=0.1 и n_learning=500 (первые 500 попыток агент просто пробует, потом пробует с вероятностью e=0.1). Оценим алгоритм согласно суммарному числу очков, которое он набирает в окружающей среде.

en1 = Environment(machines, payouts, n_trials)
	eg = eGreedy(env=en1, n_learning=500, e=0.1)
	en1.run(agent=eg)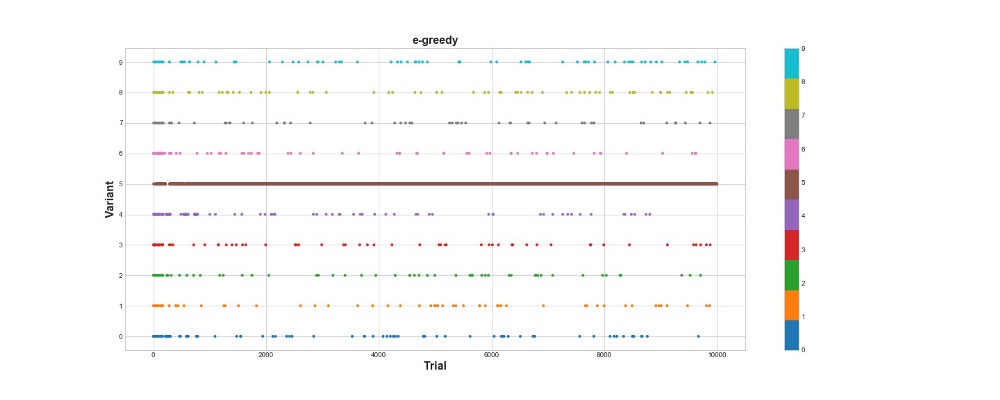

Эпсилон-жадный алгоритм набрал 788 очков, почти в 2 раза лучше, чем случайный алгоритм – супер! Второй график довольно хорошо объясняет этот алгоритм. Мы видим, что для первых 500 шагов действия распределены примерно равномерно и K выбирается случайным образом. Однако потом оно начинает сильно эксплуатировать вариант 5 – это довольно сильная опция, но не самая лучшая. Мы также видим, что 10% времени агент по-прежнему выбирает случайным образом.

Это довольно круто — мы написали всего несколько строчек кода, и вот у нас уже есть довольно мощный алгоритм, который может исследовать пространство вариантов и делать в нем близкие к оптимальному решения. С другой стороны, алгоритм не обнаружил самый лучший вариант. Да, мы может увеличить число шагов для обучения, но так мы будем тратить еще больше времени на случайный поиск, еще сильнее ухудшая итоговый результат. Также, в этот процесс по умолчанию вшита случайность – лучший алгоритм может так и не отыскаться.

Позже я запущу каждый из алгоритмов много раз, чтобы мы могли сравнить их относительно друг друга. Но пока давайте разберемся с Томпсоновским сэмплированием и проверим его в той же окружающей среде.

Томпсоновское сэмплирование (Thompson sampling)

Томпсоновское сэмплирование фундаментально отличается от эпсилон-жадного алгоритма тремя главными пунктами:

1. Оно не жадное.
2. Оно делает попытки более замысловатым путем.
3. Оно байесово.

Главным является пункт 3, пункты 1 и 2 следуют из него.

Суть алгоритма такая:

1. Задать изначальное Бета-распределение между 0 и 1 для окупаемости каждого варианта.
2. Просэмплировать варианты из этого распределения, выбрать максимальный параметр Тета.
3. Выбрать такой вариант k, какой бы ассоциировался с самым большим тета.
4. Посмотреть, сколько очков набрали, обновить параметры распределения.

Подробнее про бета-распределение можно прочитать тут.
А про его применение в Python — тут.

Код алгоритма:

	class ThompsonSampler(BaseSampler):
	
	    def __init__(self, env):
	        super().__init__(env)
	        
	    def choose_k(self):
	        # sample from posterior (this is the thompson sampling approach)
	        # this leads to more exploration because machines with > uncertainty can then be selected as the machine
	        self.theta = np.random.beta(self.a, self.b)
	        # select machine with highest posterior p of payout
	        self.k = self.variants[np.argmax(self.theta)]
	        #self.k = np.argmax(self.a/(self.a + self.b))
	        return self.k
	    
	    def update(self):
	       
	        #update dist (a, b) = (a, b) + (r, 1 - r) 
	        self.a[self.k] += self.reward
	        self.b[self.k] += 1 - self.reward # i.e. only increment b when it's a swing and a miss. 1 - 0 = 1, 1 - 1 = 0
	        
	        #self.thetaregret[self.i] = self.thetaregret[self.i]
	        #self.regret_i[self.i] = np.max(self.theta) - self.theta[self.k]
	        self.thetas[self.i] = self.theta[self.k]
	        self.thetaregret[self.i] = np.max(self.thetas) - self.theta[self.k]
	
	        self.ad_i[self.i] = self.k
	        self.r_i[self.i] = self.reward
	        self.i += 1

Формальная запись алгоритма выглядит так.

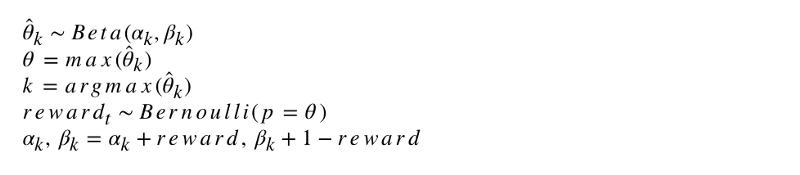
Давайте запрограммируем этот алгоритм. Как и другие агенты, ThompsonSampler наследуется от BaseSampler и определяет свои собственные методы choose_k и update. Теперь запустим нашего нового агента.

	en2 = Environment(machines, payouts, n_trials)
	tsa = ThompsonSampler(env=en2)
	en2.run(agent=tsa)

Как видно, он набрал больше, чем эпсилон-жадный алгоритм. Супер! Посмотрим на график выбора попыток. На нем видны две интересные вещи. Во-первых, агент верно обнаружил самый лучший вариант (вариант 9) и использовал его на полную катушку. Во-вторых, агент использовал и другие варианты, но более хитрым путем – примерно после 1000 попыток агент, кроме главного варианта, в основном использовал самые сильные варианты среди остальных. Иными словами, он выбирал не наобум, а более грамотно.

Почему же это работает? Все просто – неопределенность в апостериорном распределении ожидаемой выгоды для каждого варианта означает, что каждый вариант выбирается с вероятностью, примерно пропорциональной его форме, определенной параметрам альфа и бета. Иными словами, на каждой попытке Томпсоновское сэмплирование запускает вариант согласно постериорной вероятности того, что максимальная выгода именно у него. Грубо говоря, имея из распределения инофрмацию о неопределенности, агент решает, когда исследовать окружающую среду и когда использовать информацию. Например, слабый вариант с высокой постериорной неопределенностью может окупаться больше всего для данной попытки. Но для большинства попыток, чем сильнее его постериорное распределение, тем больше его среднее и тем меньше его стандартное отклонение, а значит, тем больше шансов его выбрать.

Другое замечательно свойство Томпсоновского алгоритма: так как он байесово, мы можем по его параметрам оценивать неопределенность в оценке окупаемости для каждого варианта. Ниже на графике изображены постериорные распределения в 6 разных точках и в 20000 попытках. Вы видите, как распределения постепенно начинают сходиться к варианту с самой лучшей окупаемостью.

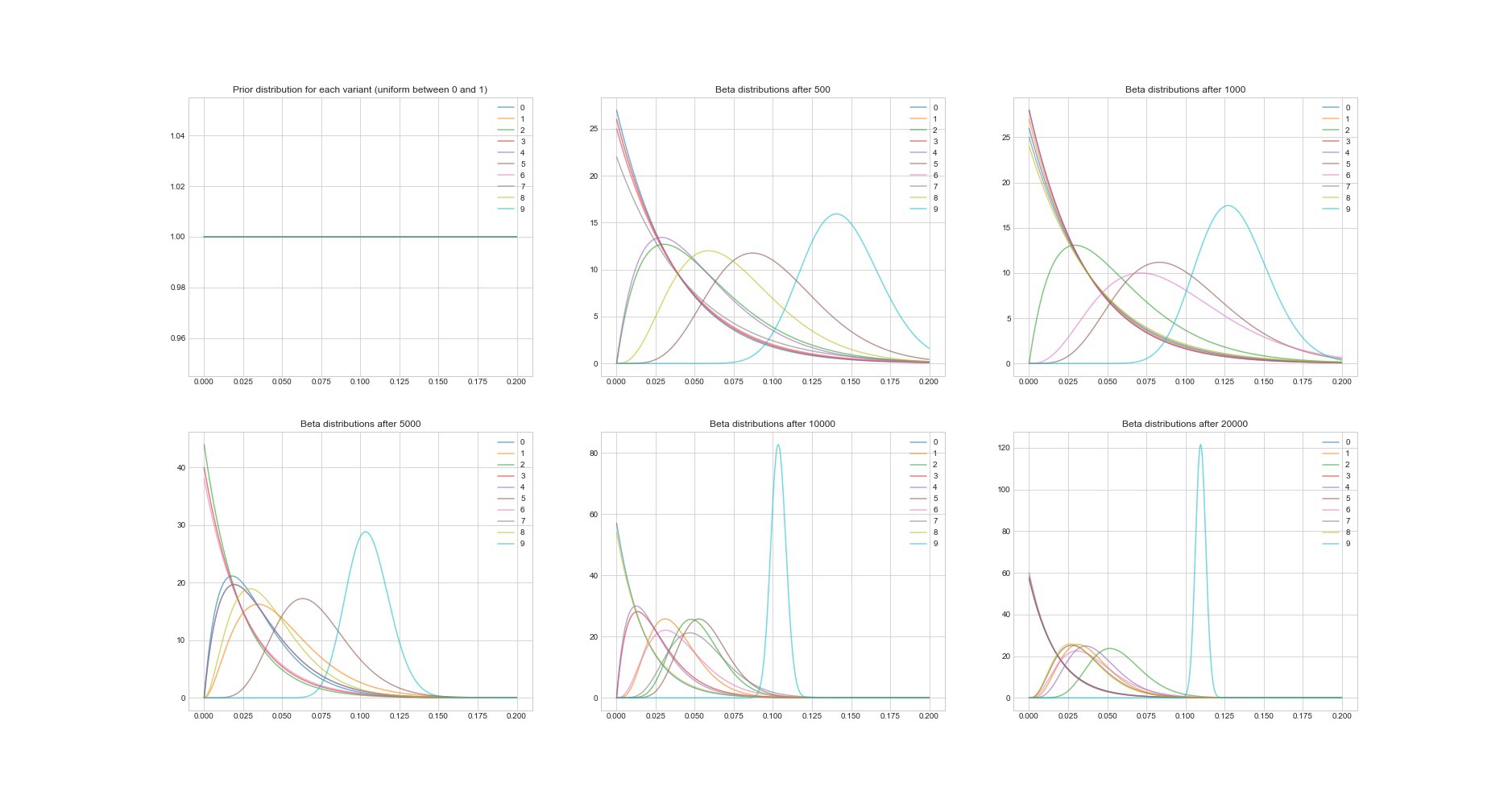
Теперь сравним все 3 агента на 100 симуляциях. 1 симуляция – это запуск агента на 10000 попытках.

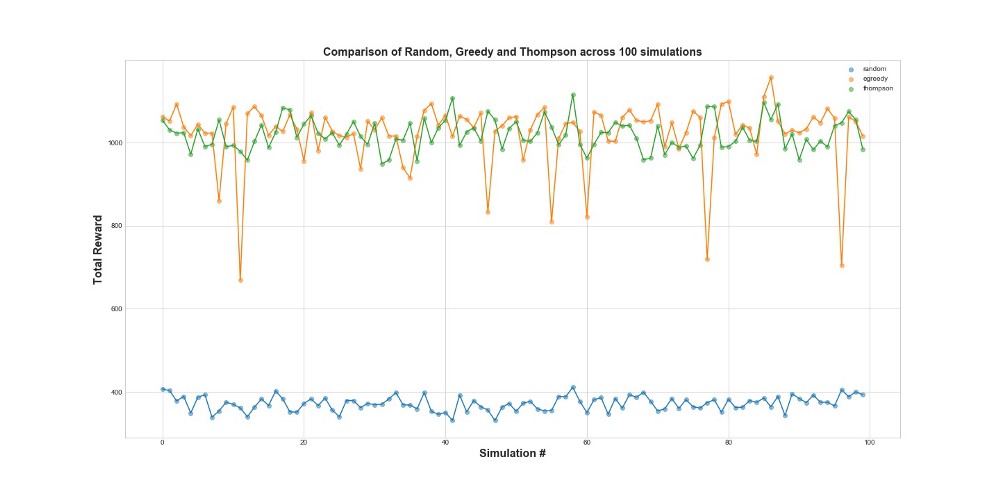
Как видно из графика, и эпсилон-жадная стратегия, и Томпсоновское сэмплирование работают сильно лучше случайного сэмплировани. Вас может удивить то, что эпсилон-жадная стратегия и Томпсоновское сэмплирование на самом деле сравнимы в том, что касается их показателей. Эпсилон-жадная стратегия может быть очень эффективной, но она более рискована, потому что может застрять на субоптимальном варианте – это можно видеть на провалах вна графике. А Томпсоновское сэмплирование не может, т.к оно делает выбор в пространстве вариантов более сложным образом.

Сожаление (regret)

Другой способ оценить, насколько алгоритм хорошо работает – это оценить сожаление (regret). Грубо говоря, чем оно меньше, по отношению к уже сделанным действиям, тем лучше. Ниже построен график суммарного сожаления и сожаления за ошибку. Еще раз – чем меньше regret, тем лучше.

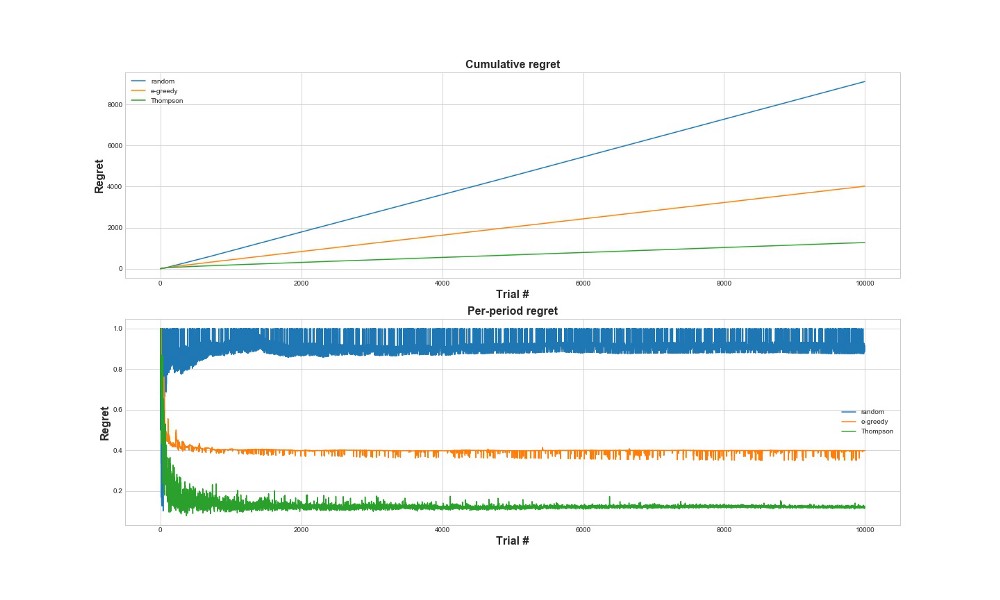
На верхнем графике мы видим суммарное сожаление, а на нижнем сожаление на попытку. Как видно из графиков, томпсоновское сэмплирование сходится к минимальному сожалению гораздо быстрее, чем эпсилон-жадная стратегия. И сходится оно к более низкому уровню. С томпсоновским сэмплированием агент сожалеет меньше, потому что он может лучше обнаруживать самый лучший вариант и лучше пробует самые многообещающие варианты – так что томпсоновское сэмплирование особенно хорошо подходит к более продвинутым случаям использования, таким, как статистические модели или нейросети для выбора k.

Выводы

Это довольно длинный технический пост. Если подытожить, мы можем использовать довольно сложные методы сэмплирования, если у нас много вариантов, которые мы хотим протестировать в реальном времени. Одно из очень хороших свойств Томпсоновского сэмплирования в том, что оно балансирует использование и исследование довольно хитрым способом. Т.е мы можем позволить ему оптимизировать распределение вариантов решений в реальном времени. Это классные алгоритмы, и они должны быть полезнее для бизнеса, чем A/B тесты.

Важно! Томпсоновское сэмплирование не означает, что вам не надо делать A/B тесты. Обычно сначала с его помощью находят лучшие варианты, и потом делают A/B тесты уже над ними.