13.10.2018 08:21
helenblack 14 2600 Источник

Реализация алгоритмов на языке Python с использованием символьных вычислений очень удобна при решении задач математического моделирования объектов, заданных дифференциальными уравнениями. Для решения таких уравнений широко используются преобразования Лапласа, которые, говоря упрощенно, позволяют свести задачу к решению простейших алгебраических уравнений.

В данной публикации предлагаю рассмотреть функции прямого и обратного преобразования Лапласа из библиотеки SymPy, которые позволяют использовать метод Лапласа для решения дифференциальных уравнений и систем средствами Python.

Сам метод Лапласа и его преимущества при решении линейных дифференциальных уравнений и систем широко освещены в литературе, например в популярном издании [1]. В книге метод Лапласа приведен для реализации в лицензионных программных пакетах Mathematica, Maple и MATLAB (что подразумевает приобретение учебным заведением этого ПО) на выбранных автором отдельных примерах.

Попробуем сегодня рассмотреть не отдельный пример решения учебной задачи средствами Python, а общий метод решения линейных дифференциальных уравнений и систем с использованием функций прямого и обратного преобразования Лапласа. При этом сохраним обучающий момент: левая часть линейного дифференциального уравнения с условиями Коши будет формироваться самим студентом, а рутинная часть задачи, состоящая в прямом преобразовании Лапласа правой части уравнения, будет выполняться при помощи функции laplace_transform().

История об авторстве преобразований Лапласа


Преобразования Лапласа (изображения по Лапласу) имеют интересную историю. Впервые интеграл в определении преобразования Лапласа появился в одной из работ Л. Эйлера. Однако в математике общепринято называть методику или теорему именем того математика, который открыл ее после Эйлера. В противном случае существовало бы несколько сотен различных теорем Эйлера.

В данном случае следующим после Эйлера был французский математик Пьер Симон де Лаплас (Pierre Simon de Laplace (1749-1827)). Именно он использовал такие интегралы в своей работе по теории вероятностей. Самим Лапласом не применялись так называемые «операционные методы» для нахождения решений дифференциальных уравнений, основанные на преобразованиях Лапласа (изображениях по Лапласу). Эти методы в действительности были обнаружены и популяризировались инженерами-практиками, особенно английским инженером-электриком Оливером Хевисайдом (1850-1925). Задолго до того, как была строго доказана справедливость этих методов, операционное исчисление успешно и широко применялось, хотя его законность ставилось в значительной мере под сомнение даже в начале XX столетия, и по этой теме велись весьма ожесточенные дебаты.

Функции прямого и обратного преобразования Лапласа


  1. Функция прямого преобразования Лапласа:
    sympy.integrals.transforms.laplace_transform(t, s, **hints).
    Функция laplace_transform() выполняет преобразования Лапласа функции f(t) вещественной переменной в функцию F(s) комплексной переменной, так что:

    $F(s)=\int_{0}^{?}f(t)e^{-st}dt.$


    Эта функция возвращает (F, a, cond), где F(s) есть преобразование Лапласа функции f(t), a<Re(s) – полуплоскость, где определена F(s), и cond– вспомогательные условия сходимости интеграла.
    Если интеграл не может быть вычислен в закрытой форме, эта функция возвращает невычисленным LaplaceTransform объекта.
    Если установить опцию noconds=True, функция возвращает только F(s).
  2. Функция обратного преобразования Лапласа:

    sympy.integrals.transforms.inverse_laplace_transform(F, s, t, plane=None, **hints).

    Функция inverse_laplace_transform() осуществляет обратное преобразование Лапласа функции комплексного переменного F(s) в функцию f(t) вещественной переменной, так что:

    $f(t)=\frac{1}{2\pi i}\int_{c-?\cdot i}^{c+?\cdot i}e^{st}F(s)ds.$


    Если интеграл не может быть вычислен в закрытой форме, эта функция возвращает невычисленным InverseLaplaceTransform объекта.

Обратное преобразование Лапласа на примере определения переходной характеристики регуляторов


Передаточная функция ПИД-регулятора имеет вид [2]:

$W(s)=(1+\frac{K_{d}\cdot T_{d}\cdot s}{1+T_{d}\cdot s})\cdot K_{p}\cdot (1+\frac{1}{T_{i}\cdot s})\cdot \frac{1}{s}.$


Напишем программу для получения уравнений для переходных характеристик ПИД- и ПИ-регуляторов для приведенной передаточной функции, и дополнительно выведем время, затраченное на выполнение обратного визуального преобразования Лапласа.

Текст программы
# Загрузка необходимых модулей:
from sympy import *
import time
import matplotlib.pyplot as plt
import numpy as np
start = time.time()
# Объявляем символьные переменные:
var('s Kp Ti Kd Td')
# Накладываем ограничение на символьную переменную времени:
var('t', positive=True)
Kp = 2
Ti = 2
Kd = 4
Td = Rational(1, 2)
# Передаточная функция ПИД-регулятора с оператором s:
fp = (1 + (Kd * Td * s) / (1 + Td*s)) * Kp * (1 + 1/(Ti*s)) * (1/s)
# Переходная характеристика ПИД-регулятора,
# получаемая методом обратного преобразования Лапласа:
ht = inverse_laplace_transform(fp, s, t)
Kd = 0
# Передаточная функция ПИ-регулятора (Kd = 0) с оператором s:
fpp = (1 + (Kd * Td * s) / (1 + Td*s)) * Kp * (1 + 1/(Ti*s)) * (1/s)
# Переходная характеристика ПИ-регулятора,
# получаемая методом обратного преобразования Лапласа:
htt = inverse_laplace_transform(fpp, s, t)
stop = time.time()
print ('Время на обратное визуальное преобразование Лапласа: %s s' % N((stop-start), 3))
# Переходим из символьной области в численную:
f = lambdify(t, ht, 'numpy')
F = lambdify(t, htt, 'numpy')
tt = np.arange(0.01, 20, 0.05)
# Построение графика:
plt.title('Переходные характеристики регуляторов \n с передаточными функциями: \n ПИД - W(s)=%s \n ПИ - W(s)=%s' % (fp, fpp))
plt.plot(tt, f(tt), color='r', linewidth=2, label='ПИД-регулятор: h(t)=%s' % ht)
plt.plot(tt, F(tt), color='b', linewidth=2, label='ПИ-регулятор: h(t)=%s' % htt)
plt.grid(True)
plt.legend(loc='best')
plt.show()


Получим:

Время на обратное визуальное преобразование Лапласа: 2.68 s



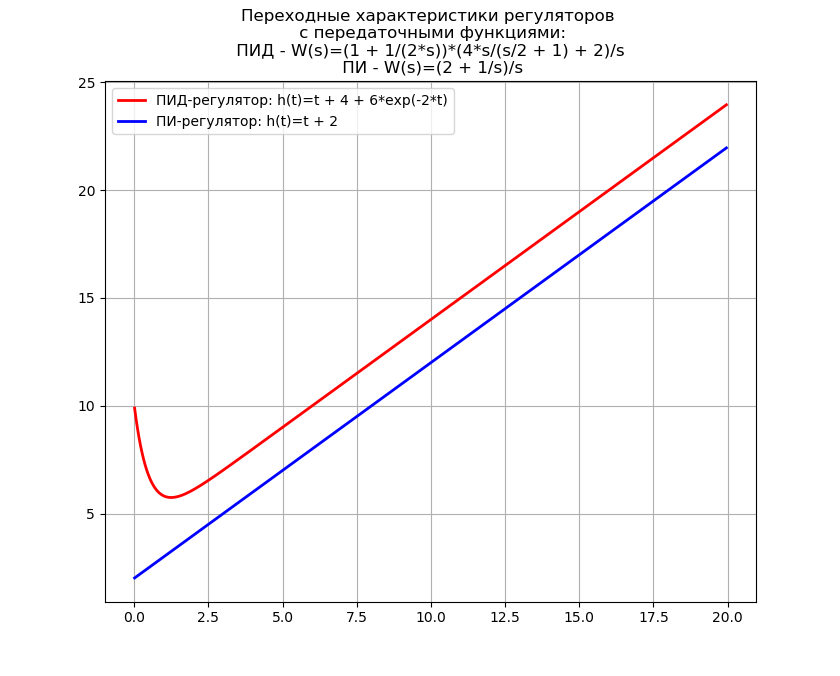
Обратное преобразование Лапласа часто используется при синтезе САУ, где Python может заменить дорогостоящих программных “монстров” типа MathCAD, поэтому приведенное использование обратного преобразования имеет практическое значение.

Преобразование Лапласа от производных высших порядков для решения задачи Коши


В продолжение нашего обсуждения будет приложение преобразований Лапласа (изображений по Лапласу) к поиску решений линейного дифференциального уравнения с постоянными коэффициентами вида:

$a\cdot x''(t)+b\cdot x'(t)+c\cdot x(t)=f(t). (1)$



Если a и b — константы, то

$L\left\{a\cdot f(t)+b\cdot q(t)\right\}=a\cdot L\left\{f(t)\right\}+b\cdot L\left\{q(t)\right\} (2)$


для всех s, таких, что существуют оба преобразования Лапласа (изображения по Лапласу) функций f(t) и q(t).

Проверим линейность прямого и обратного преобразований Лапласа с помощью ранее рассмотренных функций laplace_transform() и inverse_laplace_transform(). Для этого в качестве примера примем f(t)=sin(3t), q(t)=cos(7t), a=5, b=7 и используем следующую программу.

Текст программы
from sympy import*
var('s a b')
var('t', positive=True)
a = 5
f = sin(3*t)
b = 7
q = cos(7*t)
# Прямое преобразование a*L{f(t)}:
L1 = a * laplace_transform(f, t, s, noconds=True)
# Прямое преобразование b*L{q(t)}:
L2 = b*laplace_transform(q, t, s, noconds=True)
# Сумма a*L{f(t)}+b*L{q(t)}:
L = factor(L1 + L2)
print (L)
# Прямое преобразование L{a*f(t)+b*q(t)}:
LS = factor(laplace_transform(a*f + b*q, t, s, noconds=True))
print (LS)
print (LS == L)
# Обратное преобразование a* L^-1{f(t)}:
L_1 = a * inverse_laplace_transform(L1/a, s, t)
# Обратное преобразование b* L^-1{q(t)}
L_2 = b * inverse_laplace_transform(L2/b, s, t)
# a* L^-1{f(t)}+b* L^-1{q(t)}:
L_S = L_1 + L_2
print (L_S)
# Обратное преобразование L^-1{a*f(t)+b*q(t)}:
L_1_2 = inverse_laplace_transform(L1 + L2, s, t)
print (L_1_2)
print (L_1_2 == L_S)


Получим:

(7*s**3 + 15*s**2 + 63*s + 735)/((s**2 + 9)*(s**2 + 49))
(7*s**3 + 15*s**2 + 63*s + 735)/((s**2 + 9)*(s**2 + 49))
True
5*sin(3*t) + 7*cos(7*t)
5*sin(3*t) + 7*cos(7*t)

Приведенный код также демонстрирует однозначность обратного преобразования Лапласа.

Если предположить, что $q(t)=f'(t)$ удовлетворяет условиям первой теоремы, то из этой теоремы будет следовать, что:

$L\left\{f''(t)\right\}=L\left\{q'(t)\right\}=sL\left\{q(t)\right\}-q(0)=sL\left\{f'(t)\right\}-f'(0)=s\left[sL\left\{f(t)-f(0)\right\}\right],$


и, таким образом,

$L\left\{f''(t)\right\}=s^{2}\cdot F(s)-s\cdot f(0)-f'(0).$


Повторение этого вычисления дает

$L\left\{f'''(t)\right\}=sL\left\{f''(t)\right\}-f''(0)=s^{3}F(s)-s^{2}f(0)-sf'(0)-f''(0).$


После конечного числа таких шагов мы получаем следующее обобщение первой теоремы:

$L\left\{f^{(n)}(t)\right\}=s^{n}L\left\{f(t)\right\}-s^{n-1}f(0)-s^{n-2}f'(0)-\cdot\cdot\cdot -f^{(n-1)}(0)=$


$=s^{n}F(s)-s^{n-1}f(0)-\cdot\cdot\cdot -sf^{(n-2)}(0)-f^{(n-1)}(0). (3)$



Применяя соотношение (3), содержащее преобразованные по Лапласу производные искомой функции с начальными условиями, к уравнению (1), можно получить его решение по методу, специально разработанному на нашей кафедре при активной поддержке Scorobey для библиотеки SymPy.

Метод решения линейных дифференциальных уравнений и систем уравнений, основанный на преобразованиях Лапласа, с использованием библиотеки SymPy


Для демонстрации метода используем простое дифференциальное уравнение, описывающее движение системы, состоящей из материальной точки заданной массы, закрепленной на пружине, к которой приложена внешняя сила. Дифференциальное уравнение и начальные условия для такой системы имеют вид:

$x''+4x=\sin(3t); x(0)=1.2; x'(0)=1, (4)$


где $x(0)$ — приведенное начальное положение массы, $x'(0)$ — приведенная начальная скорость массы.

Упрощённая физическая модель, заданная уравнением (4) при ненулевых начальных условиях [1]:



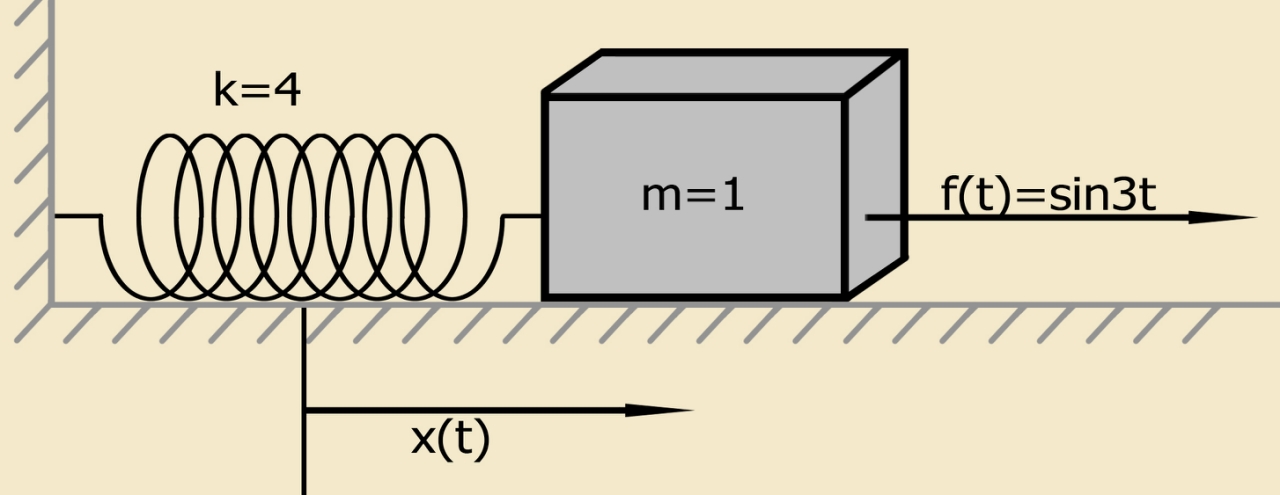
Система, состоящая из материальной точки заданной массы, закрепленной на пружине, удовлетворяет задаче Коши (задаче с начальными условиями). Материальная точка заданной массы первоначально находится в покое в положении ее равновесия.

Для решения этого и других линейных дифференциальных уравнений методом преобразований Лапласа удобно пользоваться следующей системой, полученной из соотношений (3):
$L\left\{f^{IV}(t)\right\}=s^{4}\cdot F(s)-s^{3}\cdot f(0)-s^{2}\cdot f^{I}(0)-s\cdot f^{II}(0)-f^{III}(0),$
$L\left\{f^{III}(t)\right\}=s^{3}\cdot F(s)-s^{2}\cdot f(0)-s\cdot f^{I}(0)-f^{II}(0),$
$L\left\{f^{II}(t)\right\}=s^{2}\cdot F(s)-s\cdot f(0)-f^{I}(0),$
$L\left\{f^{I}(t)\right\}=s\cdot F(s)-f(0), L\left\{f(t)\right\}=F(s).$
$L\left\{f(t)\right\}=F(s). (5) $

Последовательность решения средствами SymPy следующая:

  1. загружаем необходимые модули и явно определяем символьные переменные:

    from sympy import *
import numpy as np
import matplotlib.pyplot as plt
var('s')
var('t', positive=True)
var('X', cls=Function)

  2. указываем версию библиотеки sympy, чтобы учесть ее особенности. Для этого нужно ввести такие строки:

    import SymPy
print ('Версия библиотеки sympy – %' % (sympy._version_))

  3. по физическому смыслу задачи переменная времени определяется для области, включающей ноль и положительные числа. Задаём начальные условия и функцию в правой части уравнения (4) с её последующим преобразование по Лапласу. Для начальных условий необходимо использовать функцию Rational, поскольку использование десятичного округления приводит к ошибке.

    # Приведенное начальное положение массы:
x0 = Rational(6, 5)
# Приведенная начальная скорость:
x01 = Rational(1, 1)
g = sin(3*t)
Lg = laplace_transform(g, t, s, noconds=True)

  4. пользуясь (5), переписываем преобразованные по Лапласу производные, входящие в левую часть уравнения (4), формируя из них левую часть этого уравнения, и сравниваем результат с правой его частью:

    d2 = s**2*X(s) - s*x0 - x01
d0 = X(s)
d = d2 + 4*d0
de = Eq(d, Lg)

  5. решаем полученное алгебраическое уравнение относительно преобразования X(s) и выполняем обратное преобразование Лапласа:

    rez = solve(de, X(s))[0]
soln = inverse_laplace_transform(rez, s, t)

  6. осуществляем переход из работы в библиотеке SymPyв библиотеку NumPy:

    f = lambdify(t, soln, 'numpy')

  7. строим график обычным для Python методом:

    x = np.linspace(0, 6*np.pi, 100)
plt.title('Функция, дающая положение материальной точки \n заданной массы:\n х (t)=%s' % soln)
plt.grid(True)
plt.xlabel('t', fontsize=12)
plt.ylabel('x(t)', fontsize=12)
plt.plot(x, f(x), 'g', linewidth=2)
plt.show()


Полный текст программы:
from sympy import *
import numpy as np
import matplotlib.pyplot as plt
import sympy
var('s')
var('t', positive=True)
var('X', cls=Function)
print ("Версия библиотеки sympy – %s" % (sympy.__version__))
# Приведенное начальное положение материальной точки заданной массы:
x0 = Rational(6, 5)
# Приведенная начальная скорость материальной точки заданной массы:
x01 = Rational(1, 1)
g = sin(3*t)
# Прямое преобразование Лапласа:
Lg = laplace_transform(g, t, s, noconds=True)
d2 = s**2*X(s) - s*x0 - x01
d0 = X(s)
d = d2 + 4*d0
de = Eq(d, Lg)
# Решение алгебраического уравнения:
rez = solve(de, X(s))[0]
# Обратное преобразование Лапласа:
soln = inverse_laplace_transform(rez, s, t)
f = lambdify(t, soln, "numpy")
x = np.linspace(0, 6*np.pi, 100)
plt.title('Функция, дающая положение материальной точки \n заданной массы:\n х (t)=%s' % soln)
plt.grid(True)
plt.xlabel('t', fontsize=12)
plt.ylabel('x(t)', fontsize=12)
plt.plot(x, f(x), 'g', linewidth=2)
plt.show()


Получаем:
Версия библиотеки sympy – 1.3



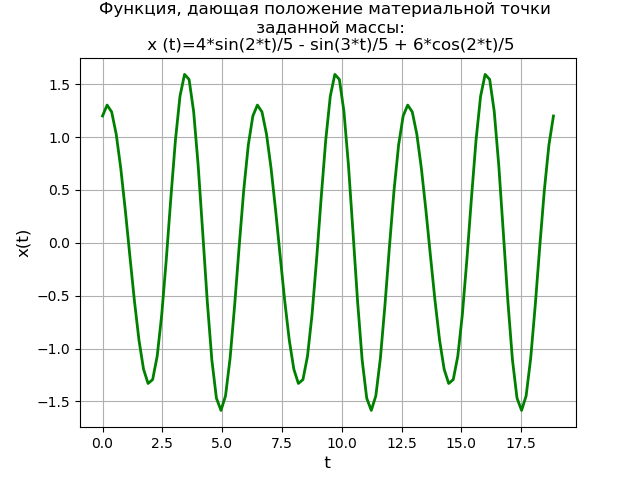
Получен график периодической функции, дающей положение материальной точки заданной массы. Метод преобразования Лапласа с использованием библиотеки SymPy дает решение не только без потребности сначала найти общее решение однородного уравнения и частное решение первоначального неоднородного дифференциального уравнения, но и без потребности использования метода элементарных дробей и таблиц Лапласа.

При этом учебное значение метода решения сохраняется за счёт необходимости использования системы (5) и перехода в NumPy для исследования решения более производительными методами.

Для дальнейшей демонстрации метода решим систему дифференциальных уравнений:
$\begin{cases}2x''+6x-2=0,\\y''-2x+2y=40\cdot \sin(3t),\end{cases} (6)$
с начальными условиями $x(0)=y(0)=y'(0)=0.$

Упрощённая физическая модель, заданная системой уравнений (6) при нулевых начальных условиях:



Таким образом, сила f(t) внезапно прилагается ко второй материальной точке заданной массы в момент времени t = 0, когда система находится в покое в ее положении равновесия.

Решение системы уравнений идентично ранее рассмотренному решению дифференциального уравнения (4), поэтому привожу текст программы без пояснений.

Текст программы
from sympy import *
import numpy as np
import matplotlib.pyplot as plt
var('s')
var('t ', positive=True)
var('X Y', cls=Function)
x0 = 0
x01 = 0
y0 = 0
y01 = 0
g = 40 * sin(3*t)
Lg = laplace_transform(g, t, s, noconds=True)
de1 = Eq(2*(s**2*X(s) - s*x0 - x01) + 6*X(s) - 2*Y(s))
de2 = Eq(s**2*Y(s) - s*y0 - y01 - 2*X(s) + 2*Y(s) - Lg)
rez = solve([de1, de2], X(s), Y(s))
rezX = expand(rez[X(s)])
solnX = inverse_laplace_transform(rezX, s, t)
rezY = expand(rez[Y(s)])
solnY = inverse_laplace_transform(rezY, s, t)
f = lambdify(t, solnX, "numpy")
F = lambdify(t, solnY, "numpy")
x = np.linspace(0, 4*np.pi, 100)
plt.title('Функции положения материальных точек заданных масс:\n x(t)=%s\n y(t)=%s' % (solnX, solnY))
plt.grid(True)
plt.xlabel('t', fontsize=12)
plt.ylabel('x(t), y(t)', fontsize=12)
plt.plot(x, f(x), 'g', linewidth=2, label='x(t)')
plt.plot(x, F(x), 'b', linewidth=2, label='y(t)')
plt.legend(loc='best')
plt.show()


Получим:



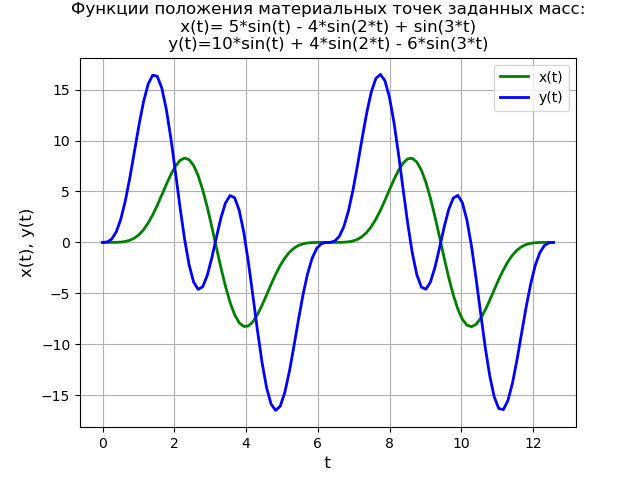
Для ненулевых начальных условий текст программы и график функций примет вид:

Текст программы
from sympy import *
import numpy as np
import matplotlib.pyplot as plt
var('s')
var('t', positive=True)
var('X Y', cls=Function)
x0 = 0
x01 = -1
y0 = 0
y01 = -1
g = 40 * sin(t)
Lg = laplace_transform(g, t, s, noconds=True)
de1 = Eq(2*(s**2*X(s) - s*x0 - x01) + 6*X(s) - 2*Y(s))
de2 = Eq(s**2*Y(s) - s*y0 - y01 - 2*X(s) + 2*Y(s) - Lg)
rez = solve([de1, de2], X(s), Y(s))
rezX = expand(rez[X(s)])
solnX = (inverse_laplace_transform(rezX, s, t)).evalf().n(3)
rezY = expand(rez[Y(s)])
solnY = (inverse_laplace_transform(rezY, s, t)).evalf().n(3)
f = lambdify(t, solnX, "numpy")
F = lambdify(t, solnY, "numpy")
x = np.linspace(0, 4*np.pi, 100)
plt.title('Функции положения материальных точек заданных масс:\n x(t)= %s \n y(t)=%s' % (solnX, solnY))
plt.grid(True)
plt.xlabel('t', fontsize=12)
plt.ylabel('x(t), y(t)', fontsize=12)
plt.plot(x, f(x), 'g', linewidth=2, label='x(t)')
plt.plot(x, F(x), 'b', linewidth=2, label='y(t)')
plt.legend(loc='best')
plt.show()




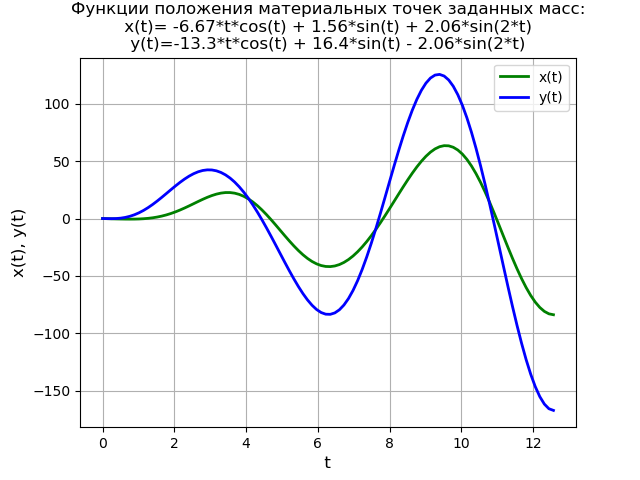
Рассмотрим решение линейного дифференциального уравнения четвёртого порядка с нулевыми начальными условиями:
$x^{(4)}+2\cdot x''+x=4\cdot t\cdot e^{t};$
$x(0)=x'(0)=x''(0)=x^{(3)}(0)=0.$

Текст программы:
from sympy import *
import numpy as np
import matplotlib.pyplot as plt
var('s')
var('t', positive=True)
var('X', cls=Function)
# Начальные условия:
x0 = 0
x01 = 0
x02 = 0
x03 = 0
g = 4*t*exp(t)
# Прямое преобразование Лапласа:
Lg = laplace_transform(g, t, s, noconds=True)
d4 = s**4*X(s) - s**3*x0 - s**2*x01 - s*x02 - x03
d2 = s**2*X(s) - s*x0 - x01
d0 = X(s)
d = factor(d4 + 2*d2 + d0)
de = Eq(d, Lg)
# Решение алгебраического уравнения:
rez = solve(de, X(s))[0]
# Обратное преобразование Лапласа:
soln = inverse_laplace_transform(rez, s, t)
f = lambdify(t, soln, "numpy")
x = np.linspace(0, 6*np.pi, 100)
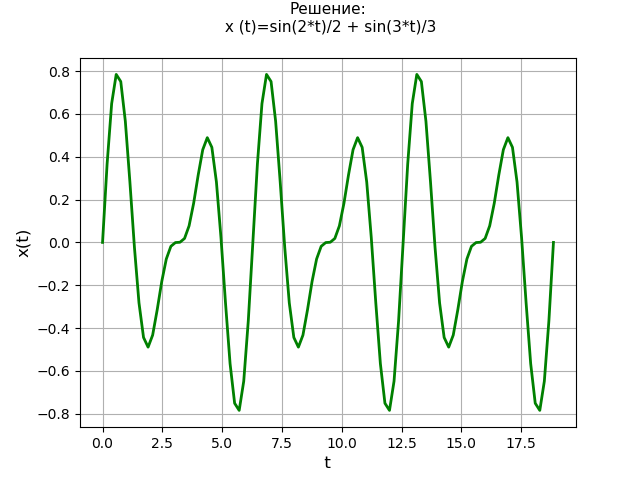
plt.title('Решение:\n х (t)=%s\n' % soln, fontsize=11)
plt.grid(True)
plt.xlabel('t', fontsize=12)
plt.ylabel('x(t)', fontsize=12)
plt.plot(x, f(x), 'g', linewidth=2)
plt.show()


График решения:



Решим линейное дифференциальное уравнение четвёртого порядка:
$x^{(4)}+13x''+36x=0;$
с начальными условиями $x(0)=x''(0)=0$, $x'(0)=2$, $x^{(3)}(0)=-13$.

Текст программы:
from sympy import *
import numpy as np
import matplotlib.pyplot as plt
var('s')
var('t', positive=True)
var('X', cls=Function)
# Начальные условия:
x0 = 0
x01 = 2
x02 = 0
x03 = -13
d4 = s**4*X(s) - s**3*x0 - s**2*x01 - s*x02 - x03
d2 = s**2*X(s) - s*x0 - x01
d0 = X(s)
d = factor(d4 + 13*d2 + 36*d0)
de = Eq(d, 0)
# Решение алгебраического уравнения:
rez = solve(de, X(s))[0]
# Обратное преобразование Лапласа:
soln = inverse_laplace_transform(rez, s, t)
f = lambdify(t, soln, "numpy")
x = np.linspace(0, 6*np.pi, 100)
plt.title('Решение:\n х (t)=%s\n' % soln, fontsize=11)
plt.grid(True)
plt.xlabel('t', fontsize=12)
plt.ylabel('x(t)', fontsize=12)
plt.plot(x, f(x), 'g', linewidth=2)
plt.show()


График решения:



Функции для решения ОДУ


Для имеющих аналитическое решение ОДУ и систем ОДУ применяется функция dsolve():
sympy.solvers.ode.dsolve(eq, func=None, hint='default', simplify=True, ics=None, xi=None, eta=None, x0=0, n=6, **kwargs)

Давайте сравним производительность функции dsolve() с методом Лапласа. Для примера возьмём следующее дифференциальное уравнение четвёртой степени с нулевыми начальными условиями:
$x^{(IV)}(t)=3\cdot x'''(t)-x(t)=4\cdot t\cdot \exp(t);$
$x(0)=x'(0)=x''(0)=x'''(0)=0.$

Программа с использованием функции dsolve():
from sympy import *
import time
import numpy as np
import matplotlib.pyplot as plt
start = time.time()
var('t C1 C2 C3 C4')
u = Function("u")(t)
# Запись дифференциального уравнения:
de = Eq(u.diff(t, t, t, t) - 3*u.diff(t, t, t) + 3*u.diff(t, t) - u.diff(t), 4*t*exp(t))
# Решение дифференциального уравнения:
des = dsolve(de, u)
# Начальные условия:
eq1 = des.rhs.subs(t, 0)
eq2 = des.rhs.diff(t).subs(t, 0)
eq3 = des.rhs.diff(t, t).subs(t, 0)
eq4 = des.rhs.diff(t, t, t).subs(t, 0)
# Решение системы алгебраических уравнений для начальных условий:
seq = solve([eq1, eq2-1, eq3-2, eq4-3], C1, C2, C3, C4)
rez = des.rhs.subs([(C1, seq[C1]), (C2, seq[C2]), (C3, seq[C3]), (C4, seq[C4])])


def F(t): return rez
f = lambdify(t, rez, 'numpy')
x = np.linspace(0, 6*np.pi, 100)
stop = time.time()
print ('Время решения уравнения с использованием функции dsolve(): %s s' % round((stop-start), 3))
plt.title('Решение с использованием функции dsolve():\n х (t)=%s\n' % rez, fontsize=11)
plt.grid(True)
plt.xlabel('Time t seconds', fontsize=12)
plt.ylabel('f(t)', fontsize=16)
plt.plot(x, f(x), color='#008000', linewidth=3)
plt.show()


Получим:

Время решения уравнения с использованием функции dsolve(): 1.437 s



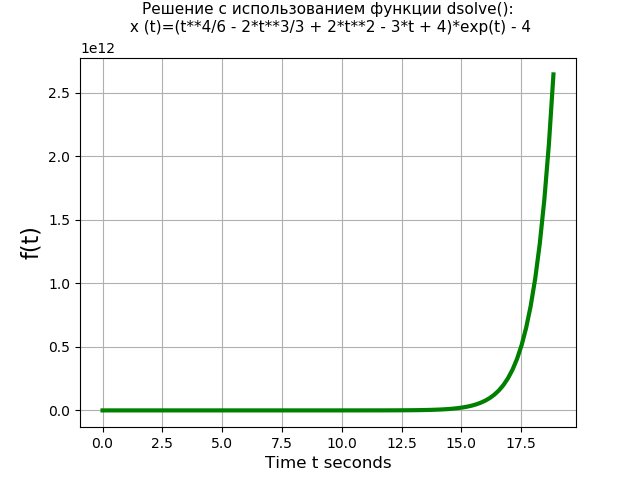
Программа с использованием преобразований Лапласа:
from sympy import *
import time
import numpy as np
import matplotlib.pyplot as plt
start = time.time()
var('s')
var('t', positive=True)
var('X', cls=Function)
# Начальные условия:
x0 = 0
x01 = 0
x02 = 0
x03 = 0
# Запись левой части дифференциального уравнения:
g = 4*t*exp(t)
# Прямое преобразование Лапласа:
Lg = laplace_transform(g, t, s, noconds=True)
d4 = s**4*X(s) - s**3*x0 - s**2*x01 - s*x02 - x03
d3 = s**3*X(s) - s**2*x0 - s*x01 - x02
d2 = s**2*X(s) - s*x0 - x01
d1 = s*X(s) - x0
d0 = X(s)
# Запись правой части дифференциального уравнения:
d = factor(d4 - 3*d3 + 3*d2 - d1)
de = Eq(d, Lg)
# Решение алгебраического уравнения:
rez = solve(de, X(s))[0]
# Обратное преобразование Лапласа:
soln = collect(inverse_laplace_transform(rez, s, t), t)
f = lambdify(t, soln, 'numpy')
x = np.linspace(0, 6*np.pi, 100)
stop = time.time()
print ('Время решения уравнения с использованием преобразования Лапласа: %s s' % round((stop-start), 3))
plt.title('Решение с использованием преобразования Лапласа:\n х (t)=%s\n' % soln, fontsize=11)
plt.grid(True)
plt.xlabel('t', fontsize=12)
plt.ylabel('x(t)', fontsize=12)
plt.plot(x, f(x), 'g', linewidth=2)
plt.show()


Получим:

Время решения уравнения с использованием преобразования Лапласа: 3.274 s



Итак, функция dsolve() (1.437 s) решает уравнение четвёртого порядка быстрее, чем выполняется решение по методу преобразований Лапласа (3.274 s) более чем в два раза. Однако при этом следует отметить, что функция dsolve() не решает системы дифференциальных уравнений второго порядка, например, при решении системы (6) с использованием функция dsolve() возникает ошибка:

from sympy import*
t = symbols('t')
x, y = symbols('x, y', Function=True)
eq = (Eq(Derivative(x(t), t, 2), -3*x(t) + y(t)), Eq(Derivative(y(t), t, 2), 2*x(t) - 2*y(t) + 40*sin(3*t)))
rez = dsolve(eq)
print (list(rez))

Получим:

raiseNotImplementedError
NotImplementedError

Данная ошибка означает, что решение системы дифференциальных уравнений с помощью функции dsolve() не может быть представлено символически. Тогда как при помощи преобразований Лапласа мы получили символическое представление решения, и это доказывает эффективность предложенного метода.

Примечание.

Для того чтобы найти необходимый метод решения дифференциальных уравнений с помощью функции dsolve(), нужно использовать classify_ode(eq, f(x)), например:

from sympy import *
from IPython.display import *
import matplotlib.pyplot as plt
init_printing(use_latex=True)
x = Symbol('x')
f = Function('f')
eq = Eq(f(x).diff(x, x) + f(x), 0)
print (dsolve(eq, f(x)))
print (classify_ode(eq, f(x)))
eq = sin(x)*cos(f(x)) + cos(x)*sin(f(x))*f(x).diff(x)
print (classify_ode(eq, f(x)))
rez = dsolve(eq, hint='almost_linear_Integral')
print (rez)

Получим:

Eq(f(x), C1*sin(x) + C2*cos(x))
('nth_linear_constant_coeff_homogeneous', '2nd_power_series_ordinary')
('separable', '1st_exact', 'almost_linear', '1st_power_series', 'lie_group', 'separable_Integral', '1st_exact_Integral', 'almost_linear_Integral')
[Eq(f(x), -acos((C1 + Integral(0, x))*exp(-Integral(-tan(x), x))) + 2*pi), Eq(f(x), acos((C1 + Integral(0,x))*exp(-Integral(-tan(x), x))))]

Таким образом, для уравнения eq=Eq(f(x).diff(x,x)+f(x),0) работает любой метод из первого списка:

nth_linear_constant_coeff_homogeneous,
2nd_power_series_ordinary

Для уравнения eq = sin(x)*cos(f(x)) + cos(x)*sin(f(x))*f(x).diff(x) работает любой метод из второго списка:

separable, 1st_exact, almost_linear,
1st_power_series, lie_group, separable_Integral,
1st_exact_Integral, almost_linear_Integral

Чтобы использовать выбранный метод, запись функции dsolve() примет вид, к примеру:

rez = dsolve(eq, hint='almost_linear_Integral')

Вывод:


Данная статья ставила своей целью показать, как использовать средства библиотек SciPy и NumPy на примере решения систем линейных ОДУ операторным методом. Таким образом, были рассмотрены методы символьного решения линейных дифференциальных уравнений и систем уравнений методом Лапласа. Проведен анализ производительности этого метода и методов, реализованных в функции dsolve().

Ссылки:

  1. Дифференциальные уравнения и краевые задачи: моделирование и вычисление с помощью Mathematica, Maple и MATLAB. 3-е издание.: Пер. с англ. — М.: ООО «И.Д. Вильяме», 2008. — 1104 с.: ил. — Парал. тит. англ.
  2. Использование обратного преобразования Лапласа для анализа динамических звеньев систем управления

Комментарии (14)


  1. rSedoy
    13.10.2018 15:32
    #19231181

    helenblack соблюдение pep8 значительно повышает читаемость кода, а избавление от «import *» еще и качество. А так да, типичный python-код от «непрограммиста» ;)


    1. homocomputeris
      13.10.2018 16:10
      #19231289

      Если код не предназначен для развёртывания, то какая разница?


      1. rSedoy
        13.10.2018 16:15
        #19231297

        Большая, если публикуют статью на популярном ресурсе, то минимум нужно стараться оформлять код в соответствии со стандартами. Кроме это, не нужно подавать плохой пример начинающим.


        1. kovserg
          13.10.2018 21:24
          #19232077

          Что говорит pep8 на каком питоне следует писать на 2-м или 3-м?
          И зачем оформлять код в соответствии со стандартами с рекомендациями?
          Или вам важнее форма, а не содержание?


          1. rSedoy
            13.10.2018 21:32
            #19232103

            Версия тут при чём? Про нее сейчас разговора и не было, хотя правильный ответ — писать надо на python3.
            Про оформление, вы вообще в теме написание программ на python? Это основы, и делается это для того чтобы ваш код нормально воспринимали другие python-программисты.


    1. strib
      13.10.2018 23:34
      #19232363

      Типичный комментарий "программиста" :) Ну покажите как надо, раз уж за качество кода душой болеете. Сообщество только спасибо скажет.


      1. rSedoy
        14.10.2018 08:56
        #19233069

        Серьезно, вы предлагает мне отформатировать этот код? Вообще-то это обязанность автора.


        1. strib
          14.10.2018 09:27
          #19233115

          Именно. Автор описал то, что понимает. И очень толково описал, но вот "не программист". И если кто-то поможет улучшить, все только выиграют. Судя по вашему комментарию вы знаете как сделать лучше.


          1. rSedoy
            14.10.2018 09:31
            #19233121

            Так для этого я или кто-то другой и не нужен, автор может сам всё сделать, инструментов достаточно, например, github.com/hhatto/autopep8


            1. helenblack Автор
              14.10.2018 17:06
              #19234339
              +1

              Спасибо за конструктивную критику. Я самоучка, поэтому ознакомление с PEP8 было для меня очень полезным. Код подправила. Действительно, выглядит лучше. Красивое лучше уродливого.
              За «import *» простите, на вкус и цвет…
              Насчет длины строк, в том же РЕР8 записано: «Некоторые команды предпочитают большую длину строки. Для кода, поддерживающегося исключительно или преимущественно этой группой, в которой могут прийти к согласию по этому вопросу, нормально увеличение длины строки с 80 до 100 символов».


    1. maisvendoo
      15.10.2018 14:41
      #19237381

      Большая часть этого кода предназначена для выполнения непосредственно в интерпретаторе, так как это не библиотека предназначенная для распространения с последующим сопровождением. Задача автора — показать возможности библиотек SciPy и NumPy для решения ОДУ в символьном виде, и с этой задачей автор справляется.


  1. vv_kuznetsov
    13.10.2018 21:38
    #19232117

    Хорошая статья. Жалко, что такого не было в то время, когда я учился. Тогда SymPi ещё не существовало, и я для того, чтобы сделать ДЗ по САУ пользовался Maxima.


    1. maisvendoo
      15.10.2018 14:43
      #19237393
      +1

      Да, много чего не было, когда мы были молодыми и глупыми. А теперь, когда мы старые и умные, и от разнообразия возможностей разбегаются глаза, тупо не хватает времени на то, чтобы охватить хотя бы малую часть… Эх…


  1. strib
    13.10.2018 23:44
    #19232375

    Отлично, спасибо. Только взялся математику освежать.
    Но как вспомню в каком количестве мы это руками на электротехнике считали...


    ЗЫ: С более аккуратным оформлением статья только выиграет. Хотя кто бы говорил...