?Здравствуйте. Я хочу рассказать про проектирование и программирование системы управления конечностями в гексаподе, построенном в Space Engineers.
Забегая вперед скажу, что всё, что касается программирования в Space Engineer, будет в следующей статье. В этой я расскажу про обратную кинематику и покажу прототип на HTML Canvas в котором я занимался отладкой алгоритмов.
Изначально было построено сочлененное шасси, а затем на нем копательный агрегат. Такая конфигурация обеспечивала контакт всх колес с поверхностью на больших неровностях, в том числе и при скручивании.

Вроде такого
Но я столкнулся с невозожностью его точно разместить на месторождении, так-как колеса часто соскальзывали вниз (проблема физики — большинство блоков (в том числе и колеса) имеют слишком малый коэффициент трения). Колесная платформа с цельноповоротными колесными модулями оказалась слишком громоздкой и страдала от периодических physics explosion. В результате было решено строить шагающего робота — а именно — гексапод, как самую стабильную шагаюшую платфрому.
С чего начнет строить гексапод нормальный человек? Наверное зайдет в игру и начнет строить тело робота с конечностями, а потом думать как это всё оживлять. Но это не наш метод (ц)
Для строения ноги была выбрана следующая схема:
Inner joint — внутренний сустав, качающийся по оси рысканья (yaw)
Mid joint и outer joint — внешние суставы, качающиеся по оси тангажа (pitch). Направление отсчета — от основания ноги к концу ноги.

Угол 0 для всех суставов означает, что нога полностью выпрямлена (прямую ногу будет проще строить в игре).
Задача — при заданной целевой точке найти такие углы поворота сустовов, что-бы конец ноги оказался в заданной точке. Значит время вспоминать тригонометрию.
Угол внутреннего сустава можно найти через арктангенс горизонтальных координат цели.
С двумя другими суставами посложнее. У нас есть длина всех суставов. Можно найти угол к горизонту и расстояние между средним суставом и землей, а так-же расстояние до целевой точки.
Дальше через теорему косинусов нужно найти углы треугольника по известным сторонам.
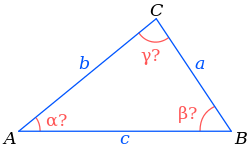

> Решение треугольников
Так это выглядит в коде:
Далее. Робот должен ходить, верно? То-есть мы должны передавать N раз в секунду каждой ноге координаты заданной позиции. С учетом того, что ног 6 и 3 из них двигаются в противофазе получается как-то сложно. Нужно ввести новый уровень абстракции.
А что если мы представим что нога движется по окружности и ей нужно передавать угол обозначающий позицию на этой окружности? Удаление в сторону становится постоянным и нужно передавать только один параметр, меняющийся циклично. Тогда целевые координыты находятся через синус и косинус.
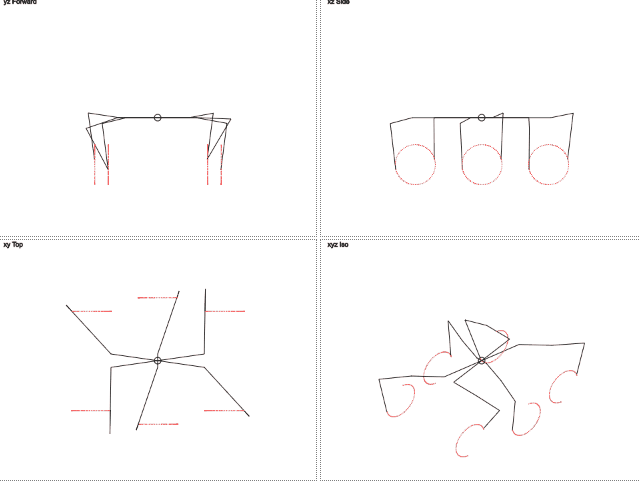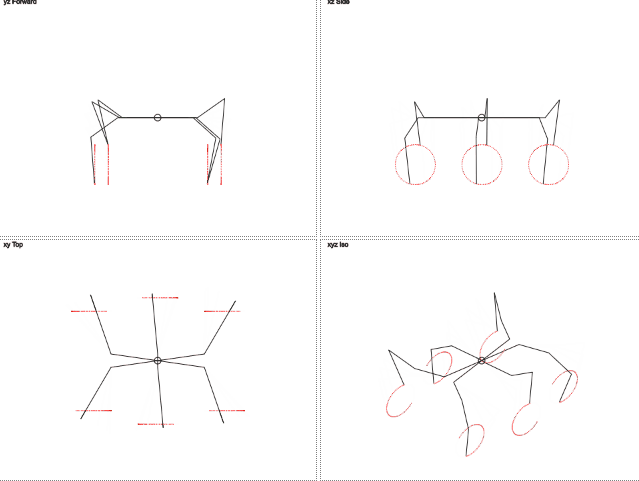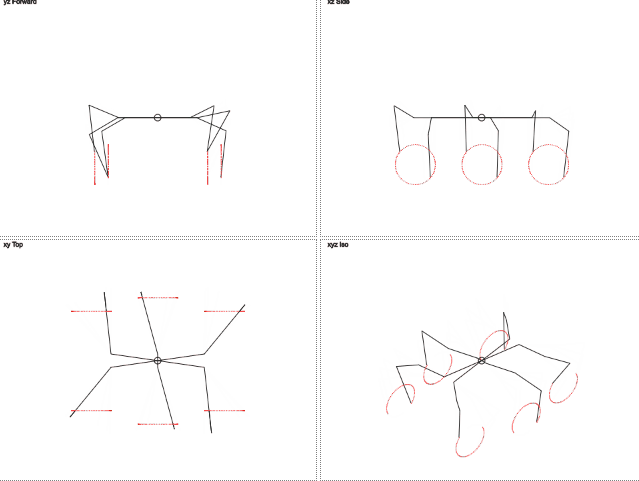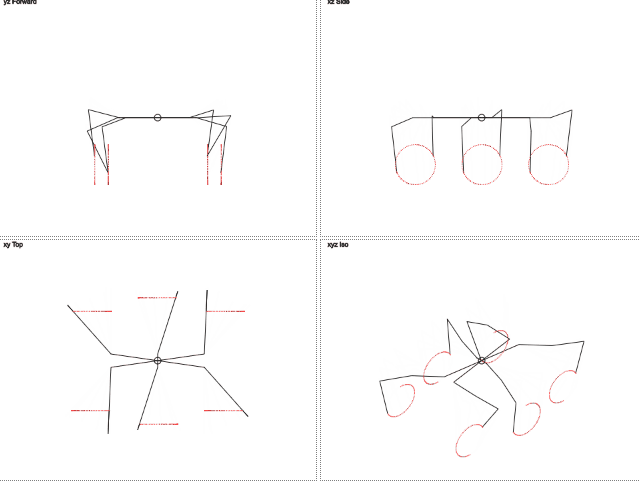
Пока достаточно
Обдумывая как всё будет работать я понял, что задача слишком сложная для того, что-бы всё заработало с первого раза (с дебагом в Space Engineers всё плохо, но об этом в следующей части).
Поэтому я решил написать визуализатор. Мне хотелось его сделать без дополнительных библиотек и иметь возможность запускать его в один клик и без привязки к окружению.
Поэтому был выбран JS + HTML Canvas.
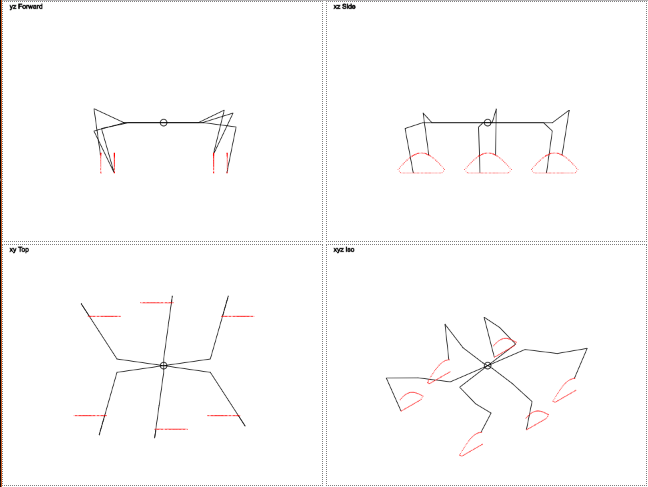
А сейчас нарисуем сову.
Код:
Результат:
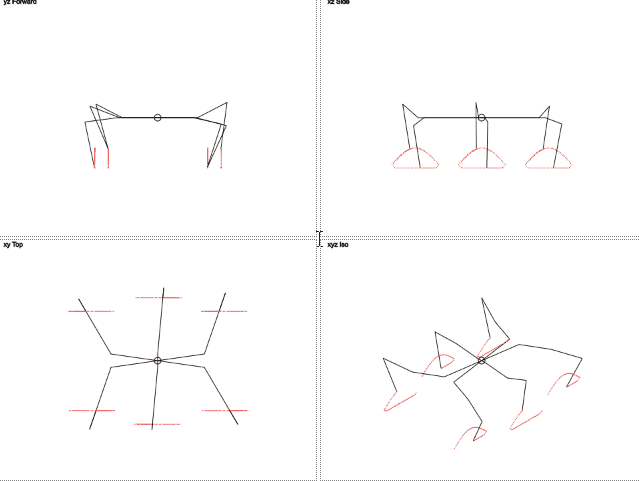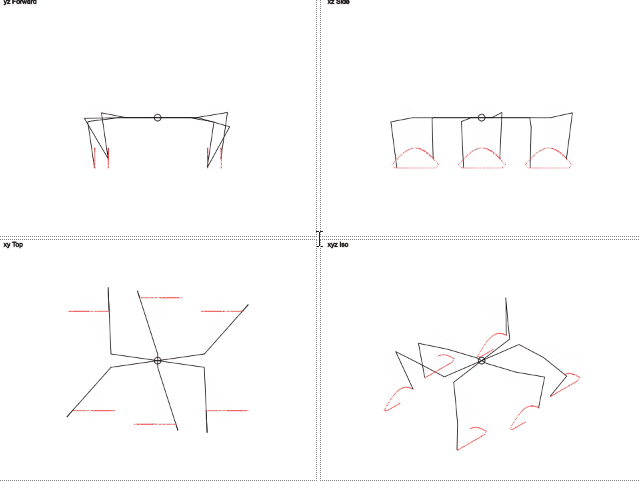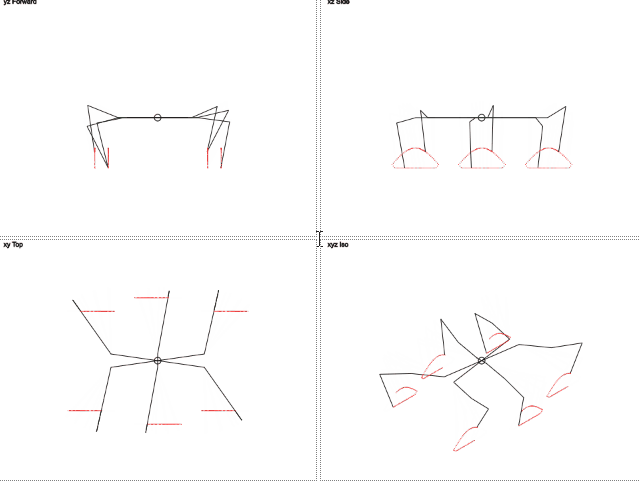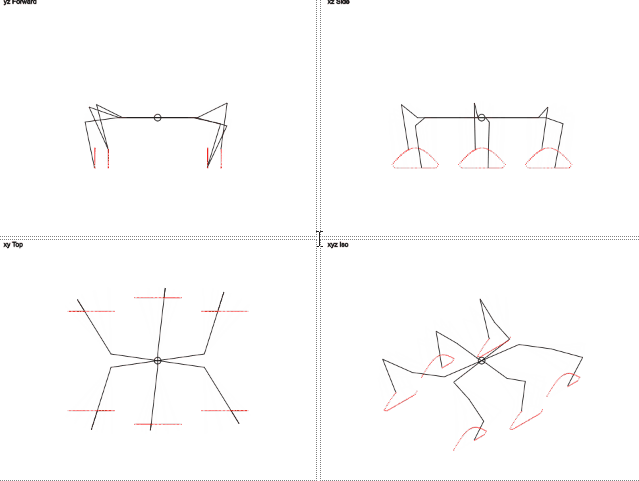
Правда миленько?
Здесь видно, что траектория движения ног отличается от окружности. Движение по вертикали напоминает урезанную синусоиду, а движение по горизонтали линейно. Это должно уменьшить нагрузку на ноги.
Теперь несколько пояснений, что происходит в коде.
Для поворота я рассмотрел 2 ситуации:
Если робот стоит — ноги двигаются по окружности.
Единственное но — движение именно по окружности сильно усложнило-бы код с текущей реализацией. Поэтому ноги двигаются по касательной к окружности.
Когда робот двигается нужно реализовать что-то вроде Ackermann steering geometry с дифференциалом.
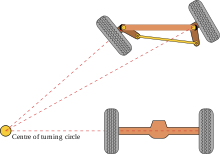
То-есть длина шага ног, двигающихся по меньшему радиусу, — меньше. А угол поворота — больше.
Что-бы реализовать изменение угла поворота для каждой ноги я придумал следующий алгоритм:
1. Считаем угол от изначального положения ноги к центру робота:
2. Считаем угол от изначального положения ноги к (центру робота + смещение, которое отвечает за поворот — это изменяемый параметр):
3. Поворачиваем шаг на разницу этих углов:
Но это не всё. Еще нужно изменять длину шага. Реализация в лоб — домножать длину шага на изменение расстояния до центра — имело фатальный недостаток — внешние ноги слишком широко шагали и начинали задевать друг друга.
Поэтому пришлось усложнить реализацию:
1. Считаем изменение расстояния до центра для каждой ноги:
0.3 — магическое число
2. Находим отношение между минимальным и максимальным изменением
Этот множитель отражает разницу между минимальным и максимальным изменением расстояния до центра. Он всегда меньше 1 и если на него домножать длину шага — она при повороте не будет увеличиваться даже для внешних по отношению к направлению поворота ног.
Вот как это работает (gif 2 мегабайта):
> Поиграться с результатом можно тут
Для более пристального изучения рекомендую сохранить содержимое в html файл и продолжить в любимом текстовом редакторе.
В следующей публикации я расскажу как заставил всё это работать в Space Engineers.
Спойлер: в Programmable Block можно писать на C# почти последней версии.
Забегая вперед скажу, что всё, что касается программирования в Space Engineer, будет в следующей статье. В этой я расскажу про обратную кинематику и покажу прототип на HTML Canvas в котором я занимался отладкой алгоритмов.

Предыстория и постановка задачи.
Изначально было построено сочлененное шасси, а затем на нем копательный агрегат. Такая конфигурация обеспечивала контакт всх колес с поверхностью на больших неровностях, в том числе и при скручивании.

Вроде такого
Но я столкнулся с невозожностью его точно разместить на месторождении, так-как колеса часто соскальзывали вниз (проблема физики — большинство блоков (в том числе и колеса) имеют слишком малый коэффициент трения). Колесная платформа с цельноповоротными колесными модулями оказалась слишком громоздкой и страдала от периодических physics explosion. В результате было решено строить шагающего робота — а именно — гексапод, как самую стабильную шагаюшую платфрому.
С чего начнет строить гексапод нормальный человек? Наверное зайдет в игру и начнет строить тело робота с конечностями, а потом думать как это всё оживлять. Но это не наш метод (ц)
Я начал с теории
Для строения ноги была выбрана следующая схема:
Inner joint — внутренний сустав, качающийся по оси рысканья (yaw)
Mid joint и outer joint — внешние суставы, качающиеся по оси тангажа (pitch). Направление отсчета — от основания ноги к концу ноги.

Угол 0 для всех суставов означает, что нога полностью выпрямлена (прямую ногу будет проще строить в игре).
Задача — при заданной целевой точке найти такие углы поворота сустовов, что-бы конец ноги оказался в заданной точке. Значит время вспоминать тригонометрию.
Угол внутреннего сустава можно найти через арктангенс горизонтальных координат цели.
const yawRad = Math.atan2(esimatedLegPosition.x, esimatedLegPosition.y);С двумя другими суставами посложнее. У нас есть длина всех суставов. Можно найти угол к горизонту и расстояние между средним суставом и землей, а так-же расстояние до целевой точки.
Дальше через теорему косинусов нужно найти углы треугольника по известным сторонам.


> Решение треугольников
Так это выглядит в коде:
getLegAngles(esimatedLegPosition) {
const yawRad = Math.atan2(esimatedLegPosition.x, esimatedLegPosition.y);
const dx = Math.hypot(esimatedLegPosition.x, esimatedLegPosition.y) - this.innerJoint.length;
const dz = this.step.idlePosition.z + esimatedLegPosition.z;
const hyp = Math.hypot(dx, dz);
if (hyp > this.midJoint.length + this.outerJoint.length) {//out of reach
hyp = this.midJoint.length + this.outerJoint.length;
}
const innerAngleRad = Math.acos((this.outerJoint.length * this.outerJoint.length - this.midJoint.length * this.midJoint.length - hyp * hyp) / (-2 * this.midJoint.length * hyp)) + Math.atan2(dz, dx);
const outerAngleRad = Math.acos((hyp * hyp - this.midJoint.length * this.midJoint.length - this.outerJoint.length * this.outerJoint.length) / (-2 * this.midJoint.length * this.outerJoint.length)) - Math.PI;
return { yaw: yawRad, midPitch: innerAngleRad, outerPitch: outerAngleRad };
}Движение
Далее. Робот должен ходить, верно? То-есть мы должны передавать N раз в секунду каждой ноге координаты заданной позиции. С учетом того, что ног 6 и 3 из них двигаются в противофазе получается как-то сложно. Нужно ввести новый уровень абстракции.
А что если мы представим что нога движется по окружности и ей нужно передавать угол обозначающий позицию на этой окружности? Удаление в сторону становится постоянным и нужно передавать только один параметр, меняющийся циклично. Тогда целевые координыты находятся через синус и косинус.

Пока достаточно
Обдумывая как всё будет работать я понял, что задача слишком сложная для того, что-бы всё заработало с первого раза (с дебагом в Space Engineers всё плохо, но об этом в следующей части).
Поэтому я решил написать визуализатор. Мне хотелось его сделать без дополнительных библиотек и иметь возможность запускать его в один клик и без привязки к окружению.
Поэтому был выбран JS + HTML Canvas.
А сейчас нарисуем сову.
Код:
Заголовок спойлера
Вектор:
Сустав:
Шаг — структура данных для управления ногой:
Нога:
Робот:
Но для отрисовки понадобятся еще несколько классов:
Обертка над Canvas:
В классе Leg есть метод для получения текущих координат суставов. Вот эти координаты мы и будем отрисовывать.
Так-же я добавил отрисовку точек, в которых находилась нога в N последних тиков.
И наконец Worker, который будет запускать симуляцию:
class Vector {
constructor(x, y, z) {
this.x = x;
this.y = y;
this.z = z;
};
distanceTo(vector) {
return Math.sqrt(Math.pow(this.x - vector.x, 2) + Math.pow(this.y - vector.y, 2) + Math.pow(this.z - vector.z, 2));
}
diff(vector) {
return new Vector(
this.x - vector.x,
this.y - vector.y,
this.z - vector.z
);
}
add(vector) {
return new Vector(
this.x + vector.x,
this.y + vector.y,
this.z + vector.z
);
}
}
Сустав:
class Joint {
constructor(angle, position, length) {
this.angle = angle;
this.position = position;
this.length = length;
this.targetAngle = angle;
this.previousAngle = angle;
this.velocity = 0;
};
setTargetAngle(targetAngle) {
this.targetAngle = targetAngle;
this.velocity = this.targetAngle - this.normalizeAngle(this.angle);
}
normalizeAngle(angle) {
while (angle <= -Math.PI) angle += Math.PI * 2;
while (angle > Math.PI) angle -= Math.PI * 2;
return angle;
}
getCurrentVelocity() {//per tick
return this.normalizeAngle(this.angle - this.previousAngle);
}
tick() {
this.previousAngle = this.angle;
this.angle = this.angle + this.velocity;
}
}
Шаг — структура данных для управления ногой:
class Step {
constructor(
idlePosition,//vector relative to inner joint
angle,//step direction
length,//step length
height,//step height
phaseShift//
) {
this.idlePosition = idlePosition;
this.angle = angle;//radians
this.length = length;
this.height = height;
this.phaseShift = phaseShift;
}
}
Нога:
class Leg {
constructor(
vehicleCenter,
innerJoint,
midJoint,
outerJoint,
step,
phaseStep
) {
this.vehicleCenter = vehicleCenter;
this.innerJoint = innerJoint;
this.midJoint = midJoint;
this.outerJoint = outerJoint;
this.step = step;
this.phaseStep = phaseStep;
this.innerJoint.length = innerJoint.position.distanceTo(midJoint.position);//calculate
this.midJoint.length = midJoint.position.distanceTo(outerJoint.position);//calculate
//this.outerJoint.length = 100;
this.joints = [innerJoint, midJoint, outerJoint];
this.preCalculateAngles();
}
preCalculateAngles() {
this.angles = {};
for (let phase = 0; phase < 360; phase += this.phaseStep) {
this.angles[phase] = this.getLegAngles(this.getEsimatedLegPosition(phase, this.step.phaseShift))
}
}
applyStepHeight(z) {
const idleYawRad = Math.atan2(this.step.idlePosition.x, this.step.idlePosition.y);
const diffHypot = Math.hypot(this.step.idlePosition.x, this.step.idlePosition.y);
const minZ = Math.abs(this.midJoint.length - this.outerJoint.length);
const maxZ = (this.midJoint.length + this.outerJoint.length) * 0.6;
if (Math.hypot(z, 0) > maxZ) {
z = z > 0 ? maxZ : -maxZ;
}
const safeY = (this.innerJoint.length + this.midJoint.length * 0.5 + this.outerJoint.length * 0.5) * Math.cos(idleYawRad);
const vAngle = Math.asin(z / safeY);
const y = safeY * Math.cos(vAngle) * Math.cos(idleYawRad);
this.step.idlePosition.z = z;
this.step.idlePosition.y = this.step.idlePosition.y > 0 ? y : -y;
this.preCalculateAngles();
}
applyStepAngle(angle) {
this.step.angle = angle;
this.preCalculateAngles();
}
applyPhase(phase/*0-360*/) {
const legAngles = this.angles[phase];
this.innerJoint.setTargetAngle(legAngles.yaw);
this.midJoint.setTargetAngle(legAngles.midPitch);
this.outerJoint.setTargetAngle(legAngles.outerPitch);
}
getEsimatedLegPosition(phase, phaseShift) {
phase = (phase + phaseShift) % 360;
const stepX = ((phase < 180 ? phase : 180 - phase % 180) / 180 - 0.5) * this.step.length;//linear movement along step direction
const stepZ = Math.max(Math.sin(phase * Math.PI / 180), -0.2) * this.step.height / 1.2;
//const stepZ = Math.max((phase > 180 ? Math.cos(phase * Math.PI / 360) + 0.9 : Math.cos((phase - 120) * Math.PI / 360)) * .9 - .1, 0) * this.step.height;
const x = this.step.idlePosition.x + stepX * Math.cos(this.step.angle);
const y = this.step.idlePosition.y + stepX * Math.sin(this.step.angle);
return new Vector(x, y, stepZ);
}
getLegAngles(esimatedLegPosition) {
const yawRad = Math.atan2(esimatedLegPosition.x, esimatedLegPosition.y);
const dx = Math.hypot(esimatedLegPosition.x, esimatedLegPosition.y) - this.innerJoint.length;
const dz = this.step.idlePosition.z + esimatedLegPosition.z;
const hyp = Math.hypot(dx, dz);
if (hyp > this.midJoint.length + this.outerJoint.length) {//out of reach
hyp = this.midJoint.length + this.outerJoint.length;
}
const innerAngleRad = Math.acos((this.outerJoint.length * this.outerJoint.length - this.midJoint.length * this.midJoint.length - hyp * hyp) / (-2 * this.midJoint.length * hyp)) + Math.atan2(dz, dx);
const outerAngleRad = Math.acos((hyp * hyp - this.midJoint.length * this.midJoint.length - this.outerJoint.length * this.outerJoint.length) / (-2 * this.midJoint.length * this.outerJoint.length)) - Math.PI;
if (isNaN(yawRad) || isNaN(innerAngleRad) || isNaN(outerAngleRad)) {
console.log(yawRad, innerAngleRad, outerAngleRad);
console.log(dx, dz);
return;
}
return { yaw: yawRad, midPitch: innerAngleRad, outerPitch: outerAngleRad };
}
getMaxMinAngles() {
const angles = [0, 90, 180, 270].map((phase) => {
return this.getLegAngles(getEsimatedLegPosition(phase, 0));
});
return {
yawMin: Math.min(angles.map((x) => { return x.yaw })),
yawMax: Math.max(angles.map((x) => { return x.yaw })),
midPitchMin: Math.min(angles.map((x) => { return x.midPitch })),
midPitchMax: Math.max(angles.map((x) => { return x.midPitch })),
outerPitchMin: Math.min(angles.map((x) => { return x.outerPitch })),
outerPitchMax: Math.max(angles.map((x) => { return x.outerPitch })),
}
}
tick() {
this.joints.forEach(function (joint) { joint.tick(); });
}
getVectors() {
const res = [];
const sinYaw = Math.sin(this.innerJoint.angle);
const cosYaw = Math.cos(this.innerJoint.angle);
let currentVector = this.vehicleCenter;
res.push(currentVector);
currentVector = currentVector.add(this.innerJoint.position);
res.push(currentVector);
currentVector = currentVector.add(new Vector(
this.innerJoint.length * sinYaw,
this.innerJoint.length * cosYaw,
0
));
res.push(currentVector);
const dxMid = Math.cos(this.midJoint.angle) * this.midJoint.length;
const dzMid = Math.sin(this.midJoint.angle) * this.midJoint.length;
currentVector = currentVector.add(new Vector(
dxMid * sinYaw,
dxMid * cosYaw,
dzMid
));
res.push(currentVector);
const c = this.midJoint.angle + this.outerJoint.angle;
const dxOuter = Math.cos(c) * this.outerJoint.length;
const dzOuter = Math.sin(c) * this.outerJoint.length;
currentVector = currentVector.add(new Vector(
dxOuter * sinYaw,
dxOuter * cosYaw,
dzOuter
));
res.push(currentVector);
return res;
}
}
Робот:
class Hexapod {
constructor(phaseStep) {
this.idleHeight = -70;
this.stepAngle = 0;
this.turnAngle = 0;
this.stepLength = 70;
this.stepHeight = 30;
this.debugPoints = [];
const vehicleCenter = new Vector(0, 0, 0);
this.legs = [
new Leg(
vehicleCenter,
new Joint(0, new Vector(-70, 10, 0), 50),
new Joint(0, new Vector(-70, 60, 0), 50),
new Joint(0, new Vector(-70, 110, 0), 70),
new Step(new Vector(-30, 90, this.idleHeight), this.stepAngle, this.stepLength, this.stepHeight, 0),
phaseStep
),
new Leg(
vehicleCenter,
new Joint(0, new Vector(-70, -10, 0), 50),
new Joint(0, new Vector(-70, -60, 0), 50),
new Joint(0, new Vector(-70, -110, 0), 70),
new Step(new Vector(-30, -90, this.idleHeight), this.stepAngle, this.stepLength, this.stepHeight, 180),
phaseStep
),
new Leg(
vehicleCenter,
new Joint(0, new Vector(0, 10, 0), 50),
new Joint(0, new Vector(0, 60, 0), 50),
new Joint(0, new Vector(0, 110, 0), 70),
new Step(new Vector(0, 100, this.idleHeight), this.stepAngle, this.stepLength, this.stepHeight, 180),
phaseStep
),
new Leg(
vehicleCenter,
new Joint(0, new Vector(0, -10, 0), 50),
new Joint(0, new Vector(0, -60, 0), 50),
new Joint(0, new Vector(0, -110, 0), 70),
new Step(new Vector(0, -100, this.idleHeight), this.stepAngle, this.stepLength, this.stepHeight, 0),
phaseStep
),
new Leg(
vehicleCenter,
new Joint(0, new Vector(70, 10, 0), 50),
new Joint(0, new Vector(70, 60, 0), 50),
new Joint(0, new Vector(70, 110, 0), 70),
new Step(new Vector(30, 90, this.idleHeight), this.stepAngle, this.stepLength, this.stepHeight, 0),
phaseStep
),
new Leg(
vehicleCenter,
new Joint(0, new Vector(70, -10, 0), 50),
new Joint(0, new Vector(70, -60, 0), 50),
new Joint(0, new Vector(70, -110, 0), 70),
new Step(new Vector(30, -90, this.idleHeight), this.stepAngle, this.stepLength, this.stepHeight, 180),
phaseStep
),
];
}
applyPhase(phase/*0-360*/) {
this.legs.forEach(function (leg) {
leg.applyPhase(phase);
});
}
changeHeight(value) {
this.legs.forEach(function (leg) {
leg.applyStepHeight(this.idleHeight + value);
}, this);
}
changeStepLength(value) {
this.stepLength += value;
this.legs.forEach(function (leg) {
leg.step.length = this.stepLength;
leg.preCalculateAngles();
}, this);
}
applyTurn1(centerX, centerY) {
const angleToAxis = Math.atan2(centerX, centerY);
const distanceToAxis = Math.hypot(centerX, centerY);
distanceToAxis = 1000/distanceToAxis;
this.legs.forEach(leg => {
const dx = leg.step.idlePosition.x + leg.innerJoint.position.x + Math.sin(angleToAxis)*distanceToAxis || 0;
const dy = leg.step.idlePosition.y + leg.innerJoint.position.y + Math.cos(angleToAxis)*distanceToAxis || 0;
const angle = Math.atan2(dy,dx);
const hypIdle = Math.hypot(dx, dy);
leg.applyStepAngle(angle+Math.PI/2);
leg.step.length = this.stepLength *hypIdle/ ((distanceToAxis || 0) + 1000);
});
}
applyTurn(centerX, centerY) {
this.stepAngle = Math.atan2(centerX, centerY);
if (this.stepAngle > Math.PI / 2) this.stepAngle -= Math.PI;
if (this.stepAngle < -Math.PI / 2) this.stepAngle += Math.PI;
const mults = this.legs.map(leg =>
Math.hypot(leg.step.idlePosition.y + leg.innerJoint.position.y, leg.step.idlePosition.x + leg.innerJoint.position.x)
/ Math.hypot(leg.step.idlePosition.y + leg.innerJoint.position.y + centerY*.3, leg.step.idlePosition.x + leg.innerJoint.position.x + centerX*.3));
const minMult = Math.min(...mults);
const maxMult = Math.max(...mults);
const mult = minMult / maxMult;
const d = Math.pow(Math.max(...this.legs.map(leg =>Math.hypot(leg.step.idlePosition.y + leg.innerJoint.position.y, leg.step.idlePosition.x + leg.innerJoint.position.x))),2)/Math.hypot(centerX,centerY);
const a = Math.atan2(centerX,centerY);
this.legs.forEach(leg => {
const dx = leg.step.idlePosition.x + leg.innerJoint.position.x;
const dy = leg.step.idlePosition.y + leg.innerJoint.position.y;
const idleAngle = Math.atan2(dx, dy) + this.stepAngle;
const turnAngle = Math.atan2(dx + centerX, dy + centerY);
const hypIdle = Math.hypot(dx, dy);
const hyp = Math.hypot(dx + centerX, dy + centerY);
leg.applyStepAngle(turnAngle - idleAngle);
leg.step.length = this.stepLength * hyp / hypIdle * mult;
});
this.debugPoints = [new Vector(Math.sin(a)*-d,Math.cos(a)*-d,0)];
}
tick() {
this.legs.forEach(function (leg) {
leg.tick();
});
}
getVectors() {
return this.legs.map(function (leg) { return leg.getVectors() });
}
}
Но для отрисовки понадобятся еще несколько классов:
Обертка над Canvas:
class Canvas {
constructor(id, label, axisSelectorX, axisSelectorY) {
const self = this;
this.id = id;
this.label = label;
this.canvas = document.getElementById(id);
this.ctx = this.canvas.getContext('2d');
this.axisSelectorX = axisSelectorX;
this.axisSelectorY = axisSelectorY;
this.canvasHeight = this.canvas.offsetHeight;
this.canvasWidth = this.canvas.offsetWidth;
this.initialY = this.canvasHeight / 2;
this.initialX = this.canvasWidth / 2;
this.traceCounter = 0;
this.maxTraces = 50;
this.traces = {};
const axisSize = 150;
this.axisVectors = [
[
new Vector(-axisSize, -axisSize, -axisSize),
new Vector(-axisSize, -axisSize, axisSize)
],
[
new Vector(-axisSize, -axisSize, -axisSize),
new Vector(-axisSize, axisSize, -axisSize)
],
[
new Vector(-axisSize, -axisSize, -axisSize),
new Vector(axisSize, -axisSize, -axisSize)
],
]
this.mouseOver = false;
this.mousePos = { x: 0, y: 0 };//relative to center
this.clickPos = { x: 0, y: 0 };//relative to center
this.canvas.addEventListener("mouseenter", function (event) {
self.mouseOver = true;
}, false);
this.canvas.addEventListener("mouseleave", function (event) {
self.mouseOver = false;
}, false);
this.canvas.addEventListener("mousemove", function (event) {
if (self.mouseOver) {
self.mousePos = { x: event.offsetX - self.initialX, y: event.offsetY - self.initialY };
}
}, false);
this.canvas.addEventListener("mouseup", function (event) {
if (self.mouseOver) {
self.clickPos = { x: event.offsetX - self.initialX, y: event.offsetY - self.initialY };
}
}, false);
};
clear(drawAxis) {
this.ctx.clearRect(0, 0, this.canvasWidth, this.canvasHeight);
this.ctx.strokeStyle = "#000000";
this.ctx.strokeText(this.label, 10, 10);
if (drawAxis) {
this.axisVectors.forEach(function (vectors, i) {
this.ctx.moveTo(this.initialX, this.initialY);
this.ctx.beginPath();
vectors.forEach(function (vector) {
this.ctx.lineTo(this.initialX + this.axisSelectorX(vector), this.initialY - this.axisSelectorY(vector));
}, this);
this.ctx.stroke();
const lastVector = vectors[vectors.length - 1];
this.traces[[this.traceCounter, i]] = lastVector
}, this);
}
}
drawVectors(vectors) {/*2d array*/
vectors.forEach(function (vectors, i) {
this.ctx.moveTo(this.initialX, this.initialY);
this.ctx.beginPath();
vectors.forEach(function (vector) {
this.ctx.lineTo(this.initialX + this.axisSelectorX(vector), this.initialY - this.axisSelectorY(vector));
}, this);
this.ctx.stroke();
const lastVector = vectors[vectors.length - 1];
this.traces[[this.traceCounter, i]] = lastVector
}, this);
for (const key in this.traces) {
const vector = this.traces[key];
this.ctx.fillStyle = "#FF0000";//red
this.ctx.fillRect(this.initialX + this.axisSelectorX(vector), this.initialY - this.axisSelectorY(vector), 1, 1);
}
this.ctx.strokeStyle = "#000000";
this.ctx.beginPath();
this.ctx.arc(this.clickPos.x + this.initialX, this.clickPos.y + this.initialY, 5, 0, 2 * Math.PI);
this.ctx.stroke();
if (this.mouseOver) {
this.ctx.strokeStyle = "#00FF00";
this.ctx.beginPath();
this.ctx.arc(this.mousePos.x + this.initialX, this.mousePos.y + this.initialY, 10, 0, 2 * Math.PI);
this.ctx.stroke();
}
this.traceCounter = (this.traceCounter + 1) % this.maxTraces;
}
drawPoints(points) {
this.ctx.fillStyle = "#00ff00";//green
points.forEach(function (point) {
this.ctx.fillRect(this.initialX + this.axisSelectorX(point), this.initialY - this.axisSelectorY(point), 3, 3);
}, this);
}
}
В классе Leg есть метод для получения текущих координат суставов. Вот эти координаты мы и будем отрисовывать.
Так-же я добавил отрисовку точек, в которых находилась нога в N последних тиков.
И наконец Worker, который будет запускать симуляцию:
class Worker {
constructor(tickTime) {
const self = this;
this.phaseStep = 5;
this.tickTime = tickTime;
const tan30 = Math.tan(Math.PI / 6);
const scale = 0.7;
this.canvases = [
new Canvas('canvasForward', 'yz Forward', function (v) { return v.y }, function (v) { return v.z }),
new Canvas('canvasSide', 'xz Side', function (v) { return v.x }, function (v) { return v.z }),
new Canvas('canvasTop', 'xy Top', function (v) { return v.x }, function (v) { return -v.y }),
new Canvas('canvasIso', 'xyz Iso', function (v) { return v.x * scale + v.y * scale }, function (v) { return v.z * scale + v.x * tan30 * scale - v.y * tan30 * scale }),
];
this.bot = new Hexapod(this.phaseStep);
this.phase = 0;
this.focus = true;
window.addEventListener('focus', function () {
console.log('focus');
self.focus = true;
});
window.addEventListener('blur', function () {
console.log('blur');
self.focus = false;
});
this.start();
}
tick(argument) {
const canvasForward = this.canvases[0];
const bot = this.bot;
if (canvasForward.mouseOver) {
bot.changeHeight(-canvasForward.mousePos.y);
} else {
bot.changeHeight(0);
}
const canvasTop = this.canvases[2];
if (canvasTop.mouseOver) {
bot.applyTurn(-canvasTop.mousePos.x, -canvasTop.mousePos.y);
} else {
bot.applyTurn(0, 0);
}
this.phase = (this.phase + this.phaseStep) % 360;
bot.applyPhase(this.phase);
bot.tick();
const vectors = bot.getVectors();
this.canvases.forEach(function (c) {
c.clear(false);
c.drawVectors(vectors);
c.drawPoints(bot.debugPoints);
});
}
start() {
this.stop();
this.interval = setInterval((function (self) {
return function () {
if (self.focus) {
self.tick();
}
}
})(this), this.tickTime);
}
stop() {
clearInterval(this.interval);
}
}
Результат:

Правда миленько?
Здесь видно, что траектория движения ног отличается от окружности. Движение по вертикали напоминает урезанную синусоиду, а движение по горизонтали линейно. Это должно уменьшить нагрузку на ноги.
Теперь несколько пояснений, что происходит в коде.
Как научить робота поворачивать?
Для поворота я рассмотрел 2 ситуации:
Если робот стоит — ноги двигаются по окружности.
Единственное но — движение именно по окружности сильно усложнило-бы код с текущей реализацией. Поэтому ноги двигаются по касательной к окружности.
Когда робот двигается нужно реализовать что-то вроде Ackermann steering geometry с дифференциалом.

То-есть длина шага ног, двигающихся по меньшему радиусу, — меньше. А угол поворота — больше.
Что-бы реализовать изменение угла поворота для каждой ноги я придумал следующий алгоритм:
1. Считаем угол от изначального положения ноги к центру робота:
const idleAngle = Math.atan2(dx, dy) + this.stepAngle;2. Считаем угол от изначального положения ноги к (центру робота + смещение, которое отвечает за поворот — это изменяемый параметр):
const turnAngle = Math.atan2(dx + centerX, dy + centerY);3. Поворачиваем шаг на разницу этих углов:
leg.applyStepAngle(turnAngle - idleAngle);Но это не всё. Еще нужно изменять длину шага. Реализация в лоб — домножать длину шага на изменение расстояния до центра — имело фатальный недостаток — внешние ноги слишком широко шагали и начинали задевать друг друга.
Поэтому пришлось усложнить реализацию:
1. Считаем изменение расстояния до центра для каждой ноги:
const mults = this.legs.map(leg =>
Math.hypot(leg.step.idlePosition.y + leg.innerJoint.position.y, leg.step.idlePosition.x + leg.innerJoint.position.x)
/ Math.hypot(leg.step.idlePosition.y + leg.innerJoint.position.y + centerY*.3, leg.step.idlePosition.x + leg.innerJoint.position.x + centerX*.3));0.3 — магическое число
2. Находим отношение между минимальным и максимальным изменением
const minMult = Math.min(...mults);
const maxMult = Math.max(...mults);
const mult = minMult / maxMult;Этот множитель отражает разницу между минимальным и максимальным изменением расстояния до центра. Он всегда меньше 1 и если на него домножать длину шага — она при повороте не будет увеличиваться даже для внешних по отношению к направлению поворота ног.
const hypIdle = Math.hypot(dx, dy);
const hyp = Math.hypot(dx + centerX, dy + centerY);
leg.step.length = this.stepLength * hyp / hypIdle * mult;
Вот как это работает (gif 2 мегабайта):
gif 2 мегабайта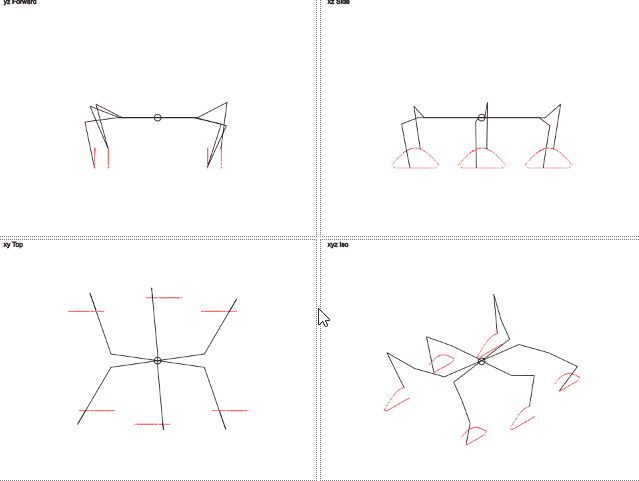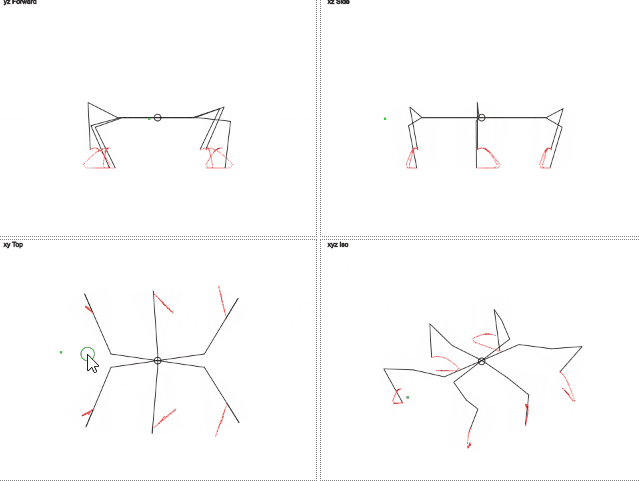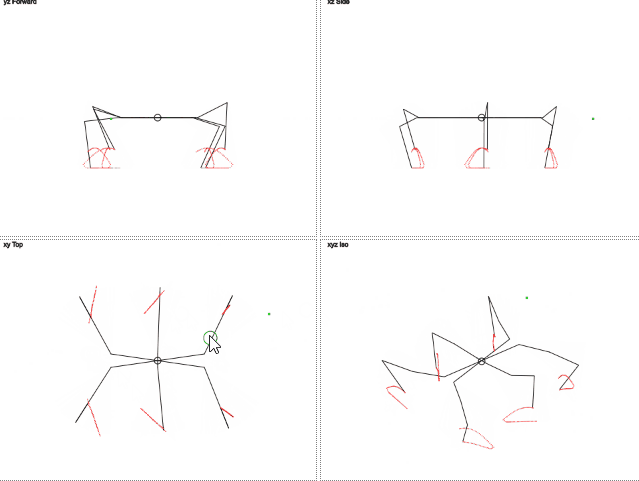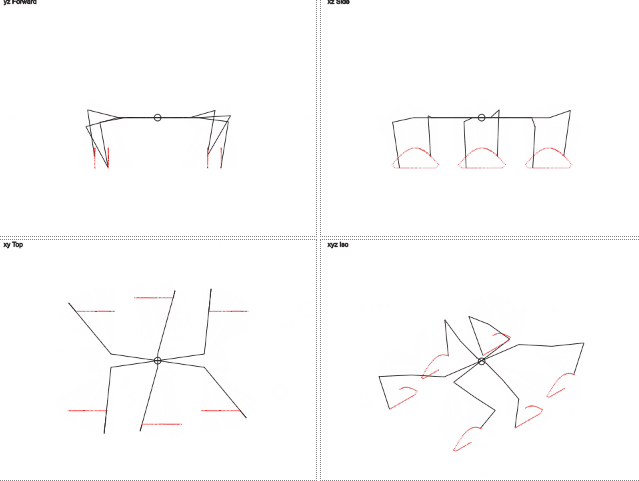

> Поиграться с результатом можно тут
Для более пристального изучения рекомендую сохранить содержимое в html файл и продолжить в любимом текстовом редакторе.
В следующей публикации я расскажу как заставил всё это работать в Space Engineers.
Спойлер: в Programmable Block можно писать на C# почти последней версии.


springimport
Интересно, вы программировали ради любопытства или нашли хорошее применение машине с такой конструкцией?
Вроде все уже согласились что одним из самых оптимальных вариантов является летающая машина.
tgwt
экономие энергии, если поставить большой контейнер и заполнить его рудой, то потребуется много атмосферников, чтобы это все не падало, в следствие чего, потребуется больше источников питания (батарей, реакторов)
RiseOfDeath
В это игре в этом нет смысла. Кроме случаев когда у вас какие-то экзотические настройки, из-за чего уран в жестком дефиците.
По сабжу — идея автора годная. Возникает только вопрос гексапод должен определять высоту постановки ноги, как он это делает? Насколько я помню (давно не играл, увы) реальных способов узнать где земля (без использования модов) в игре нет.
tgwt
ну либо отсутствие урана на планете (на сервере, на котором я сейчас играю), либо устанавливать кучу атмосферников, чем еще больше увеличивать размер буровика, что не очень нужно
Vindicar
Поставить камеру/сенсор с малым радиусом действия на конец ноги?
RiseOfDeath
А она разве реагирует на террейн? В вики об этом вообще ничего не сказано.
conKORD Автор
У камеры через Programmable block можно использовать raycast — получается что-то вроде лидара.
А у сенсора с определением поверхности проблемы — на планете он срабатывает на высоте метров 100.
Vindicar
Там вроде можно уменьшить радиус — все равно не срабатывает?
conKORD Автор
На астероиды сенсор срабатывает нормально, но на поверхность планеты будет срабатывать метрах на ста даже если уменьшить его дальность действия до минимума. Баг.
conKORD Автор
>гексапод должен определять высоту постановки ноги, как он это делает?
Правильный ответ — никак. В этом и состоит преимущество шестиного робота по сравнению с четырехногим или двуногим. В любой момент времени 3 ноги касаются земли и робот сам выравнивается относительно поверхности.
conKORD Автор
Верно. Шагоход имеет практическое применение только на планете с малым количеством урана.
Вот такая штука работает на одной солнечной панели.
tgwt
а почему не попробовали шасси вместо колес на ноги нацепить? возможно, это позволит ползать по скалам, надо бы попробовать. этот проект есть в библиотеке?
conKORD Автор
Landing gears?
Не подошли по следующим причинам:
1) Они повреждаются или разрушаются при столкновении с поверхностью. Я нашел только 2 модуля, которые могут служить подошвой ноги: колеса и дрель. Но дрель имеет слишком низкий коэффициент трения — робот скатывался вниз даже на слабом уклоне.
2) В процессе шага конец ноги поворачивается относительно поверхности — пришлось-бы добавить еще 2 ротора что-бы это компенсировать.
Проект уже есть в workshop, но я хочу дать на него ссылку вместе с объяснениями — что и как работает. То-есть в следующей статье.
conKORD Автор
Скорее ради спортивного интереса. И вдохновившись работами Boston Dynamics.
hatari90
Если расстояние до ископаемых велико, то с точки зрения энергозатрат выгоднее всего транспортная платформа на колесах, несущая буровую летающую машину и контейнеры для хранения руды. Если ограничиваться одним аппаратом, то будет маленькая вместимость и большие затраты на поддержание машины в воздухе как при бурении, так и на дорогу между месторождением и базой.
Но в обычных условиях, как выше писали, в этом нет смысла, колеса слишком неудобные, и разгоняться на такой машине будет нельзя, в отличие от летающей.
RiseOfDeath
У колесной платформы есть существенный недостаток — неадкватно низкое трение скольжения (вообще выглядит как баг). Т.е. едет она вроде бы почти адекватно, а вот стоять на месте категорически не может. Как следствие такая платформа будет соскальзывать даже при минимальном уклоне.
Хотя как вариант поддамкрачивать ее — приехал, выставил Landing Gear на поршнях и все, типа база.
А вообще, в инжах выгоднее всего копать астероиды — затраты на перемещение минимальны — только разгон и торможение. Плюс возможность удаленного управления на любом расстоянии.
hatari90
Насчет landing gear — да, вариант.
Если база на планете, то подниматься на почти 40 километров — банально долго по времени. Плюс необходимость водородных двигателей. Хотя в космосе есть огромный плюс — без всякого программирования штатный автопилот при выставлении точки координат довезет куда нужно, пока вы наливаете чай. На планете опция обсчета коллизий работала очень так себе.
Да и когда в последний раз заходил, как раз добавили парашюты, которые по идее должны сильно экономить топливо на посадке.
RiseOfDeath
Я как-то эксперементировал с «ударной» посадкой — рассчет был на то, что капсула не может разогнаться более 100м/с (по-умолчанию) и не совсем адкватной модели подвреждений при ударе (по факту удар сильно гасит скорость, и повреждаются несколько наружних слоев блоков) — можно пожертвовать небольшим кол-вом металла для разрашаемой противоударной защиты контейнера (в виде моргенштерна) (примечание такая конструкция не выдержит падения на склон горы т.к. разрушится при качении)
А на счет подъема — зачем он вам? Ретрансляторы для копания + проекторы для сборки «дропподов» возволят вам кидаться в вашу базу ресурсами, без необходимости подниматься. К тому же, опять же, лед есть и на астероидах, так что можно и на взлет/посадку ресурсы собирать в космосе.
Vindicar
Снимаю шляпу. Моего терпения хватило только на примитивную леталку из точки A в точку B без обхода препятствий.
8street
Интересно, все же, как будет реализовано в SE. Давно туда не заходил и не знал, что добавили язык программирования.
Vindicar
Там нормальный C#. Вот только разработку забросили ради Medieval Engineers. =(
tgwt
ну как забросили, сделали возможность наконец то нормально поиграть в мультиплеере
artyomtch
Ах, ностальгия… Лет 15 назад именно это было темой моего проекта по… компьютерной графике :) Помню, тоже развлекался сначала с формулами вычисления координат «стопы» относительно крепления «бедра» для таких-то углов сочленений и длин «бедра» и «голени» вместе с обратными формулами — нахождения необходимых углов сочленений для такой-то координаты «стопы». Затем, как и Вы — перешел к следующему уровню абстракции: ходьбе. Тоже вначале чесал репу, а потом дошло, что все на самом деле просто: касающиеся земли ноги просто смещаются на Х назад, в то время как другие три ноги совершают движение на 2Х вперед, сопровождающееся подъемом по той или иной дуге. Затем пошли алгоритмы разворотов и поиска маршрута по неровной поверхности (правда, без обхода препятствий). Даже скриншоты остались:
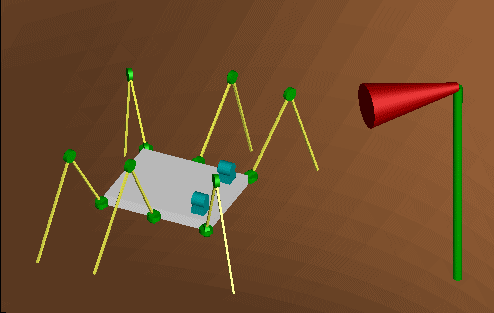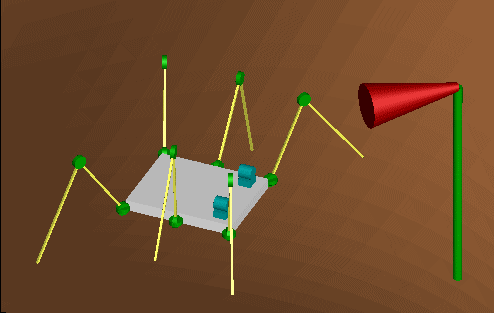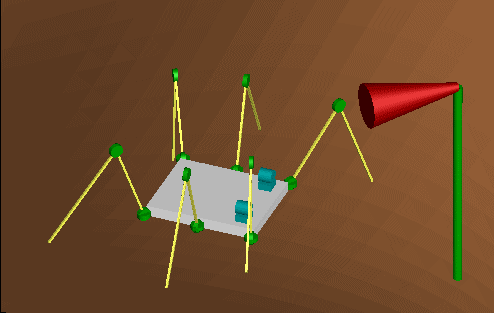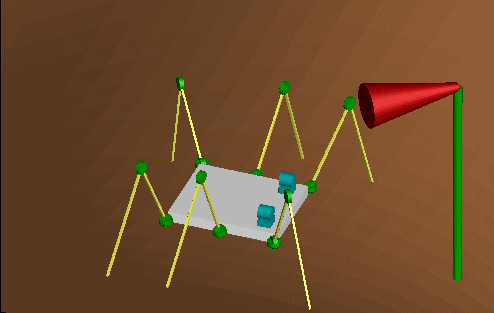

А потом, в виду того, что это был проект не по роботике, а по компьютерной графике… препод попросил перенести алгоритм на нечто живое:
Было очень приятно перечитать статью, тем более, что проект был «из спортивного интереса». Я все хотел эти алгоритмы перенести в железо… на нечто, что можно пощупать руками… но потом как-то не срослось.