Однажды я готовился к Ludum Dare и сделал простую игру, где использовал пиксельные шейдеры (других в движок Phaser не завезли).

color = pixelShader(x, y, ...other attributes)

Потестировав, кинул ссылку другу, и получил от него вот такой скриншот с вопросом "а это нормально?"

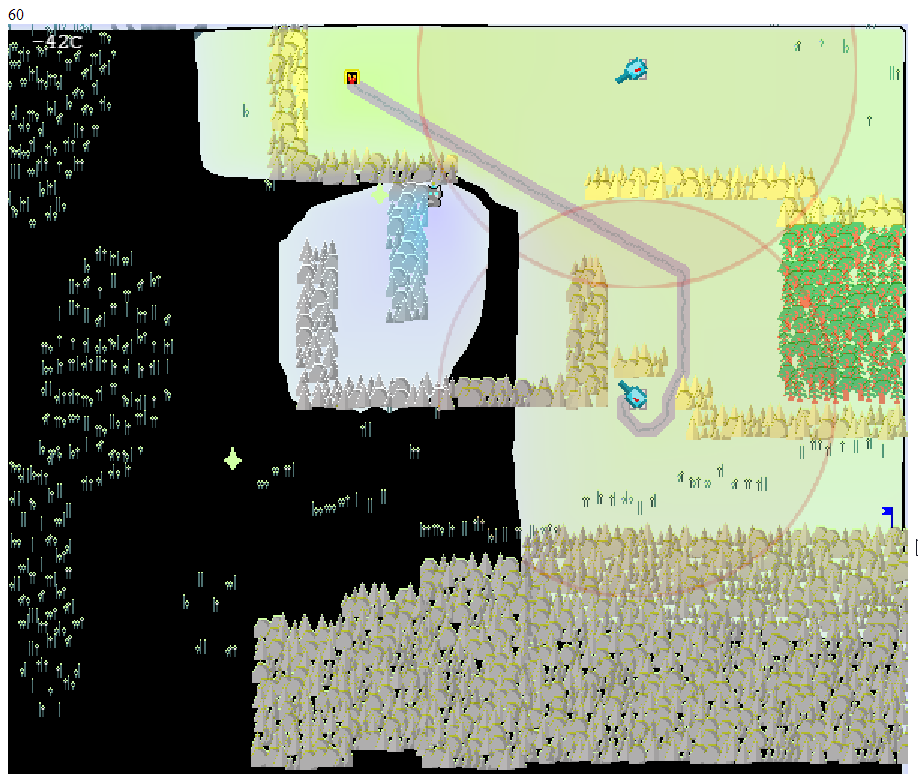
Нет, это было ненормально. Посмотрев внимательно код шейдера, я обнаружил ошибку в вычислениях:

if (t < M) {
    realColor = mix(color1,color2, pow(1. - t / R1, 0.5));
}

Т.к. константа R1 была меньше чем M, то в некоторых случаях в первом аргументе pow получалось число меньше нуля. Квадратный корень из отрицательного числа — штука загадочная, по крайней мере для стандарта GLSL. Мою видеокарту ничего не смутило, и она как-то выпуталась из этого положения (похоже, вернув из pow 0), а вот у друга она оказалась более разборчивой.

И тут я задумался: а могу ли я избежать таких проблем в будущем? От ошибок никто не застрахован, особенно таких, которые не воспроизводятся локально. Юнит-тесты на GLSL не напишешь. В то же время преобразования внутри шейдера довольно простые — умножения, деления, синусы, косинусы… Неужели нельзя отследить значения каждой переменной и убедиться, что ни при каких условиях не происходит выхода за допустимые границы значений?

Так я решил попробовать сделать статический анализ для GLSL. Что из этого получилось — можно прочитать под катом.

Сразу предупрежу: какого-то законченного продукта получить не удалось, только учебный прототип.

Предварительный анализ

Немного проштудировав существующие статьи на эту тему (и попутно выяснив, что тема называется Value Range Analysis), я порадовался тому, что у меня именно GLSL, а не какой-то другой язык. Посудите сами:

• никакой "динамики" — ссылок на функции, интерфейсов, автоматически выводимых типов и прочего
• никакой прямой работы с памятью
• никаких модулей, линковки, позднего связывания — исходный код шейдера доступен целиком
  для входящих значений как правило хорошо известны диапазоны
• немного типов данных, да и те крутятся вокруг float. int/bool используются крайне редко, и за ними не так важно следить
• if-ы и циклы используются достаточно редко (из-за проблем с производительностью). циклы если и используются, то чаще простые счетчики для прохода по массиву или повторению некоего эффекта несколько раз. Вот такого ужаса никто в GLSL писать не будет (надеюсь).

//взято из статьи - https://homepages.dcc.ufmg.br/~fernando/classes/dcc888/ementa/slides/RangeAnalysis.pdf
k = 0 
while k < 100: 
  i = 0 
  j = k 
  while i < j: 
    i = i + 1 
    j = j – 1 
   k = k + 1

В общем, с учетом ограничений GLSL задача выглядит решаемой. Основной алгоритм сводится к следующему:

1. разобрать код шейдера и выстроить последовательность команд, меняющих значения каких-либо переменных
2. зная начальные диапазоны для переменных, пройти по последовательности, обновляя диапазоны при их изменении
3. если диапазон нарушает какие-то заданные границы (например, в pow может прийти отрицательное число, или в "выходной цвет" gl_FragColor в красный компонент придет что-то больше 1.), надо показать предупреждение

Используемые технологии

Здесь у меня был долгий и мучительный выбор. С одной стороны мой основной скоуп — это проверка WebGL-ных шейдеров, поэтому почему бы и не javascript — чтобы запускать все в браузере при разработке. С другой стороны, я давно планирую слезть с Phaser-а и попробовать другой движок типа Unity или LibGDX. Там тоже будут шейдеры, а вот javascript-а уже не будет.

А с третьей стороны задача делалась в первую очередь для развлечения. А лучшее на свете развлечение — это зоопарк. Поэтому:

1. разбор GLSL-кода сделан на javascript. Просто я довольно быстро нашел библиотеку для парсинга GLSL в AST именно на нем, да и тестовый UI вроде как привычнее делать вебовским. AST превращается в последовательность команд, которая отправляется во...
2. … вторую часть, которая написана на C++ и компилируется в WebAssembly. Я решил так: если вдруг захочу прикрутить этот свой анализатор к какому-то еще движку, с библиотекой на C++ это должно быть сделать проще всего.

Все, теперь можно ехать.

Коротко о модели

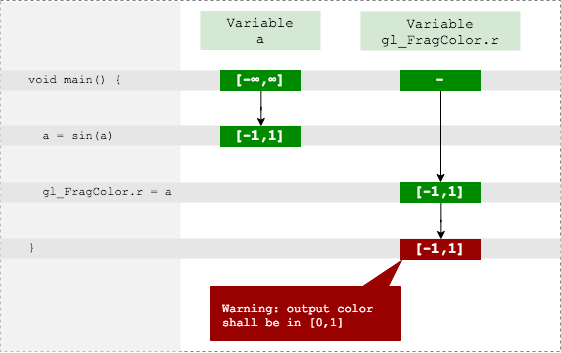
Анализатор держит в памяти список переменных, которые встречаются в шейдере, и для каждого хранит текущий возможный диапазон значений (типа [0,1] или [1,?) ).

Анализатор принимает на вход поток операций типа такой:

cmdId: 10
opCode: sin
arguments: [1,2,-,-,3,4,-,-]

Тут у нас вызывается функция sin, на вход ей подаются переменные с id = 3 и 4, а результат записывается в переменные 1 и 2. Этот вызов соответствует GLSL-ному:

vec2 a = sin(b);

Обратите внимание на пустые аргументы (помечены как "-"). В GLSL почти все встроенные функции перегружены для разных наборов входных типов, т.е. существуют sin(float), sin(vec2), sin(vec3), sin(vec4). Для удобства я привожу все перегруженные версии к одному виду — в данном случае sin(vec4).

На выход анализатор выдает список изменений для каждой переменной, вроде

cmdId: 10
branchId: 1
variable: 2
range: [-1,1]

Что означает "переменная 2 в строке 10 в ветке 1 имеет диапазон от -1 до 1 включительно" (что такое ветка (branch) мы поговорим чуть позже). Теперь можно красиво подсвечивать диапазоны значений в исходном коде.

Хорошее начало

Когда AST-дерево уже начало худо-бедно превращаться в список команд, настала пора реализовывать стандартные функции и методы. Их довольно много (и еще у них до кучи перегрузок, как я писал выше), но в целом у них предсказуемые преобразования диапазонов. Скажем, вот для такого примера все довольно очевидно получается:

uniform float angle;  // -> (-?,?)
//...
float y = sin(angle); // -> [-1,1]
float ynorm = 1 + y;  // -> [0,2]
gl_FragColor.r = ynorm / 2.; // -> [0,1]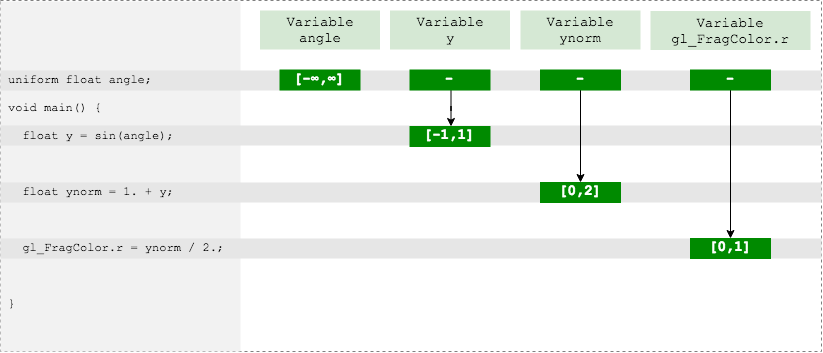

Красный канал выходного цвета у нас в допустимом диапазоне, ошибок нет.

Если покрыть побольше встроенных функций, то для половины шейдеров и такого анализа хватит. Но что насчет второй половины — с условиями, циклами и функциями?

Ветвления

Возьмем для примера такой шейдер.

uniform sampler2D uSampler;
uniform vec2 uv; // [0,1]

void main() {
  float a = texture2D(uSampler, uv).a;  // -> [0,1]
  float k;  // -> ?
  if (a < 0.5) {
     k = a * 2.;
  } else {
     k = 1. - a;
  }
  gl_FragColor = vec4(1.) * k;
}

Переменная a у нас берется из текстуры, и поэтому значение этой переменной лежит от 0 до 1. А вот какие значения может принимать k?

Можно пойти по простому пути и "обьединить ветки" — посчитать диапазон в каждом из случаев и выдать общее. Для ветки if получаем k = [0,2], а для ветки else k = [0,1]. Если объединить, получается [0,2], и надо выдавать ошибку, т.к. в выходной цвет gl_FragColor попадают значения больше 1.

Однако это явный false alarm, а для статического анализатора нет ничего хуже ложных срабатываний — если его не отключат после первого крика "волки", то после десятого точно.

Значит, нам нужно обрабатывать обе ветки порознь, причем в обеих ветках мы должны уточнить диапазон переменной a (хотя формально его никто не менял). Вот как это может выглядеть:

Ветка 1:

if (a < 0.5) {    //a = [0, 0.5)
   k = a * 2.;    //k = [0, 1)
   gl_FragColor = vec4(1.) * k;
}

Ветка 2:

if (a >= 0.5) {    //a = [0.5, 1]
   k = 1. - a;     //k = [0, 0.5]
   gl_FragColor = vec4(1.) * k;
}

Таким образом, когда анализатор встречает некое условие, которое по-разному себя вести в зависимости от диапазона, то он создает ветки (branches — бранчи) для каждого из случаев. В каждом случае он уточняет диапазон исходной переменной и движется дальше по списку команд.

Стоит уточнить, что ветки в данном случае не связаны с конструкцией if-else. Ветки создаются при разбиении диапазона какой-то переменной на под-диапазоны, и причиной может стать необязательно условный оператор. Например, функция step тоже создает ветки. Следующий GLSL-шейдер делает то же самое, что предыдущий, только не использует ветвление (что, кстати, лучше в плане производительности).

float a = texture2D(uSampler, uv).a;
float k = mix(a * 2., 1. - a, step(0.5, a));
gl_FragColor = vec4(1.) * k;

Функция step должна вернуть 0 если a < 0.5 и 1 в противном случае. Поэтому здесь тоже будут созданы ветки — аналогичные предыдущему примеру.

Уточнение других переменных

Рассмотрим чуть видоизмененный предыдущий пример:

float a = texture2D(uSampler, uv).a; // -> [0,1]
float b = a - 0.5;  // -> [-0.5, 0.5]
if (b < 0.) {
   k = a * 2.;      // k,a -> ?
} else {
   k = 1. - a;
}

Здесь нюанс в следующем: ветвление происходит по переменной b, а вычисления происходят с переменной a. То есть внутри каждой ветки будет корректное значение диапазона b, но совершенно ненужное, и оригинальное значение диапазона a, совершенно некорректное.

Однако анализатор видел, что диапазон b был получен вычислением из a. Если запомнить эту информацию, то при ветвлении анализатор может пройтись по всем исходным переменным и уточнить их диапазон, выполнив обратное вычисление.

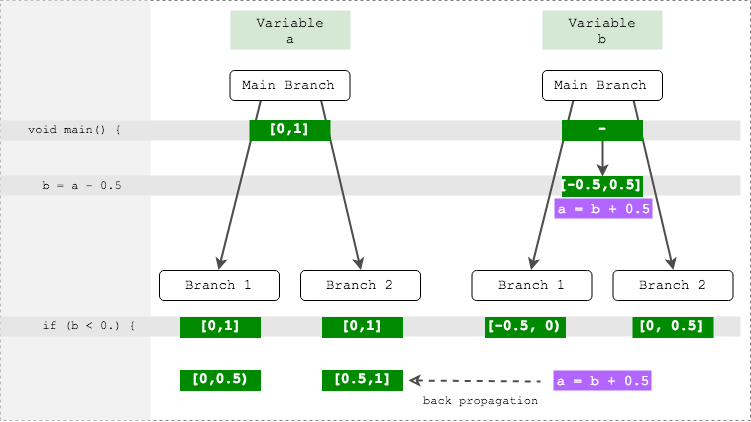
Функции и циклы

В GLSL нет виртуальных методов, указателей на функции и даже рекурсивных вызовов, так что каждый вызов функции однозначен. Поэтому проще всего вставить тело функции в месте вызова (заинлайнить, иначе говоря). Это будет полностью соответствовать последовательности выполнения команд.

С циклами все посложнее, т.к. формально GLSL полностью поддерживает си-подобный цикл for. Однако чаще всего циклы используются в простейшем варианте, вот таком:

for (int i = 0; i < 12; i++) {}

Такие циклы несложно "развернуть", т.е. вставить тело цикла 12 раз друг за другом. В итоге, подумав, я решил пока что поддержать только такой вариант.

Плюсом этого подхода является то, что команды можно выдавать потоком в анализатор, не требуя от него запоминания каких-то фрагментов (типа тел функций или циклов) для дальнейшего переиспользования.

Всплывшие проблемы

Проблема #1: сложность или невозможность уточнения

Выше мы рассматривали случаи, когда при уточнения значения по одной переменной мы делали выводы о значениях другой переменной. И эта задача решаема, когда участвуют операции типа сложения/вычитания. Но, скажем, как быть с тригонометрией? Например такое условие:

float a = getSomeValue();
if (sin(a) > 0.) {
   //Чему тут считать равным a?
}

Как посчитать диапазон a внутри if? Получается бесконечный набор диапазонов с шагом пи, с которым потом работать будет очень неудобно.

А еще может быть такая ситуация:

float a = getSomeValue(); // [-10,10]
float b = getAnotherValue(); //[-20, 30]
float k = a + b;
if (k > 0) {
  //a? b?
}

Уточнить диапазоны a и b в общем случае будет нереально. А, значит, возможны ложные срабатывания.

Проблема #2: Зависимые диапазоны

Рассмотрим такой пример:

uniform float value //-> [0,1];    
void main() {
    float val2 = value - 1.;
    gl_FragColor = vec4(value - val2);
}

Для начала анализатор считает диапазон переменной val2 — и он ожидаемо оказывается [0,1] - 1 == [-1, 0]

Однако затем, считая value - val2, анализатор не учитывает, что val2 был получен из value, и работает с диапазонами так, будто бы они независимы друг от друга. Получает [0,1] - [-1,0] = [0,2], и рапортует об ошибке. Хотя в реальности он должен был получить константу 1.

Возможное решение: хранить для каждой переменную не просто историю диапазонов, но и всю "родословную" — от каких переменных была зависимость, какие операции, и так далее. Другое дело, что "разворачивать" эту родословную будет делом непростым.

Проблема #3: Диапазоны, зависимые неявно

Вот пример:

float k = sin(a) + cos(a); 

Здесь анализатор предположит, что диапазон k = [-1,1] + [-1,1] = [-2,2]. Что неверно, т.к. sin(a) + cos(a) для любых a лежит в диапазоне [-v2, v2].

Результат вычисления sin(a) формально никак не зависит от результата вычисления cos(a). Однако они зависят от одного и того же диапазона a.

Итоги и выводы

Как оказалось, сделать value range analysis даже для такого простого и узкоспециализированного языка, как GLSL — задача непростая. Покрытие фич языка еще можно усилить: поддержка массивов, матриц и всех встроенных операций — задача чисто техническая, просто требующая затрат по времени. А вот как решать ситуации с зависимостями между переменными — вопрос пока для меня неясный. Без решения этих проблем неизбежны ложные срабатывания, шум от которых может в итоге перевесить пользу от статического анализа.

С учетом того, с чем я столкнулся, я не особо удивлен отсутствию каких-то известных инструментов для value range analysis в других языках — в них проблем явно больше, чем в относительно простом GLSL. При этом на других языках можно хотя бы юнит-тесты писать, а тут — никак.

Альтернативным решением может стать компиляция из других языков в GLSL — вот тут недавно была статья про компиляцию из kotlin. Тогда можно писать юнит-тесты на исходный код и покрывать все граничные условия. Или сделать “динамический анализатор”, который будет прогонять те же данные, что идут в шейдер, через оригинальный код на kotlin и предупреждать о возможных проблемах.

Так что на этом этапе я остановился. Библиотеки увы не получилось, но может быть кому-то этот прототип пригодится.

Репозиторий на github, для ознакомления:

• https://github.com/AlexeyGrishin/glsl-value-range-analysis

Попробовать:

• https://alexeygrishin.github.io/glsl-value-range-analysis/html/

Бонус: особенности сборки webassembly с разными флагами компилятора

Изначально я делал анализатор без использования stdlib — по старинке, с массивами и указателями. На тот момент я сильно переживал за размер выходного wasm-файла, хотелось чтобы он был маленьким. Но начиная с некоторого момента я начал испытывать дискомфорт и потому решил перевести все на stdlib — умные указатели, нормальные коллекции, вот это все.

Соответственно я получил возможность сравнить результаты сборки двух версий библиотеки — с stdlib и без нее. Ну и еще посмотреть, насколько хорошо/плохо cheerp (и используемый им clang) оптимизирует код.

Поэтому я скомпилировал обе версии с разными наборами флагов оптимизации (-O0, -O1, -O2, -O3, -Os и -Oz), и для некоторых из этих версий сделал замеры скорости анализа 3000 операций с 1000 ветвлениями. Согласен, не самый большой пример, но для сравнительного анализа имхо достаточно.

Что получилось по размеру wasm файла:

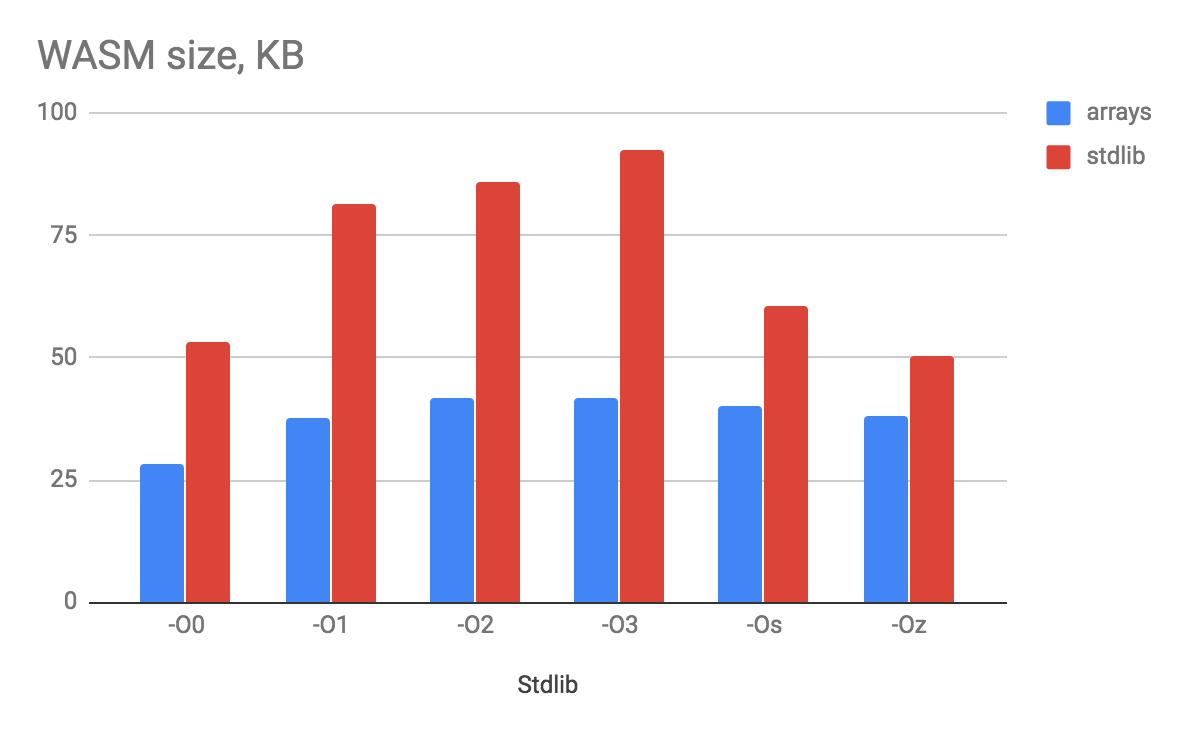
Удивительно, но по размеру вариант с "нулевой" оптимизацией получается лучше, чем почти все остальные. Я предположу, что в O3 имеет место агрессивный инлайн всего на свете, что и раздувает бинарник. Ожидаемо версия без stdlib получилась покомпактнее, но не настолько, чтобы терпеть такие унижения лишать себя удовольствия работы с удобными коллекциями.

По скорости выполнения:

Теперь мне видно, что -O3 не зря ест свой хлеб, если сравнивать с -O0. При этом разница между версиями с stdlib и без нее практически отсутствует (я делал по 10 замеров, думаю на большем числе разница вообще исчезла бы).

Стоит отметить 2 момента:

• На графике представлены средние значения из 10 последовательных запусков анализа, однако на всех тестах самый первый анализ длился в 2 раза дольше остальных (т.е., скажем, 120мс, а следующие уже в районе 60мс). Вероятно происходила какая-то инициализация WebAssembly.
• С флагом -O3 я отхватывал какие-то ужасно странные баги, которых не ловил для других флагов. Например, функции min и max внезапно начинали работать одинаково — как min.

Заключение

Всем спасибо за внимание.
Пусть значения ваших переменных никогда не выходят за отведенные рамки.
А вот вы — выходите.