Introduction
We have created a synthesizable verilog code for calculating an integer cube root of an integer number via binary search algorithm. This code had been tested on Cyclone IV FPGA board. Here you can read about implementation and understand how things works.
Github link: Cube root
What Is a Cube Root?
Cube root of a number y is a number x such that
Examples:
So, in our implementation we use an integer cube root.
It means that a cube root of an integer number x is an another integer number a such that:
Examples:
Main Logic
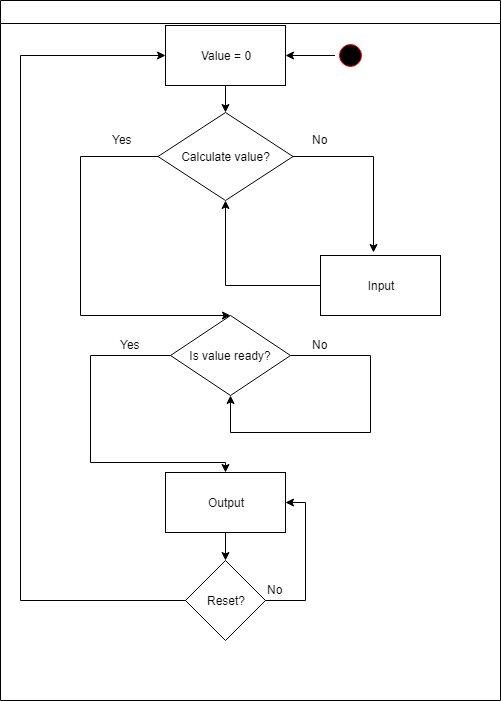
Main module is responsible for all the actions with a number during input.
It has 4 possible actions:
- multiply increment by 10
- divide increment by 10(increment is always not less than 1)
- increase number
- decrease number
Main module
module cube_root(
input inc,
input sub,
input next,
input prev,
input enter,
input clk,
output wire [7:0] leds,
output wire [7:0] control
);
reg signed [31:0] exit;
wire ready;
wire [31:0] res;
reg zero = 0;
// input //
reg inc1 = 0;
reg next1 = 0;
reg prev1 = 0;
reg sub1 = 0;
reg enter1 = 0;
reg [31:0] decimal = 1;
//////////
reg [31:0] to_display;
display_bcd display(
.clk(clk),
.value(ready == 0 ? exit : res),
.control(control),
.leds(leds)
);
calculate calc(
.clk(clk),
.ready_to_calc(~enter),
.num(exit),
.ready(ready),
.res(res)
);
always @(posedge clk)
begin
if (enter == 1) begin
if ((inc1 == 1'b0) && (~inc == 1'b1)) begin
exit = exit + decimal;
end
inc1 = ~inc;
if ((sub1 == 1'b0) && (~sub == 1'b1)) begin
if (exit > 0) begin
exit = exit - decimal;
end
end
sub1 = ~sub;
if ((next1 == 1'b0) && (~next == 1'b1)) begin
decimal = decimal * 10;
end
next1 = ~next;
if ((prev1 == 1'b0) && (~prev == 1'b1)) begin
if (decimal >= 1 && decimal <= 9) begin
decimal = 1;
end else begin
decimal = decimal / 10;
end
end
prev1 = ~prev;
end else begin
if (ready == 1'b1) begin
exit = 0;
decimal = 1;
end
end
end
endmodule In the main module cube_root there are also two other modules: calculate and display_bcd. The first one doing all required calculations, while the second module is responsible for displaying input and output values during the programm execution.
Now, let's understand how they work.
Calculate module
Calculation module uses a binary search algorithm. And when all the calculations are done it sets ready variable to 1. It is a signal for display module to output the answer.
Calculate module
module calculate(
input clk,
input ready_to_calc,
input [31:0] num,
output reg ready,
output [31:0] res
);
integer mid;
integer start;
integer final;
integer counter;
assign res = mid;
always @(posedge clk)
begin
if (ready_to_calc == 1) begin
if (ready == 0) begin
mid = (start + final )/2;
if ((mid*mid*mid) > num) begin
final = mid;
end else begin
start = mid;
end
if (counter == 27) begin
ready = 1;
counter = 0;
end else begin
counter = counter + 1;
end
end
end else begin
final = 465;
start = 0;
ready = 0;
counter = 0;
end
end
endmodule
Why this module does exactly 27 iterations?
— Maximum input number is 99999999. So, maximum possible number of iterations is
Why upper bound of binary search is initialized by 465?
— Because it is maximum number we can get as a result.
Display module
This module is responsible for the performance. It uses eight eight-segment displays and they are manipulated by 16 pins. Where 8 pins are «in charge» for particular leds on display and other 8 ones are control segments, they represent distinct digits.
So, we pass an integer value that we want to display to this module. Then, it passes this value to the Binary_to_BCD module which converts binary number to the Binary Coded Decimal using Double Dabble algorithm. After that, converted value becomes easy to display.
Display module
module display_bcd (
input clk,
input [31:0] value,
output [7:0] control,
output [7:0] leds
);
bcd_convert #(32, 8) bcd_convert(
.i_Clock(clk),
.i_Binary(value_temp),
.i_Start(1'b1),
.o_BCD(bcd_number),
.o_DV(bcd_ready)
);
integer delay = 0;
integer final_bcd;
reg [2:0] ctrl = 0;
reg [4:0] digit;
wire bcd_ready;
wire [31:0] bcd_number;
wire [31:0] digits;
assign digits = final_bcd;
wire [31:0] value_temp;
assign value_temp = value;
assign control = ~(1 << ctrl);
assign leds = ~
(digit == 0 ? 8'b00111111 :
(digit == 1 ? 8'b00000110 :
(digit == 2 ? 8'b01011011 :
(digit == 3 ? 8'b01001111 :
(digit == 4 ? 8'b01100110 :
(digit == 5 ? 8'b01101101 :
(digit == 6 ? 8'b01111101 :
(digit == 7 ? 8'b00000111 :
(digit == 8 ? 8'b01111111 :
(digit == 9 ? 8'b01101111 :
8'b00000000))))))))));
always @(posedge clk)
begin
if (bcd_ready)
final_bcd = bcd_number;
case(ctrl)
0: digit = digits[3:0];
1: digit = digits[31:4] ? digits[7:4] : 10;
2: digit = digits[31:8] ? digits[11:8] : 10;
3: digit = digits[31:12] ? digits[15:12] : 10;
4: digit = digits[31:16] ? digits[19:16] : 10;
5: digit = digits[31:20] ? digits[23:20] : 10;
6: digit = digits[31:24] ? digits[27:24] : 10;
7: digit = digits[31:28] ? digits[31:28] : 10;
endcase
delay = delay + 1;
if (delay == 10000)
ctrl = ctrl + 1;
end
endmodule BCD convert
module bcd_convert
#(parameter INPUT_WIDTH,
parameter DECIMAL_DIGITS)
(
input i_Clock,
input [INPUT_WIDTH-1:0] i_Binary,
input i_Start,
output [DECIMAL_DIGITS*4-1:0] o_BCD,
output o_DV
);
parameter s_IDLE = 3'b000;
parameter s_SHIFT = 3'b001;
parameter s_CHECK_SHIFT_INDEX = 3'b010;
parameter s_ADD = 3'b011;
parameter s_CHECK_DIGIT_INDEX = 3'b100;
parameter s_BCD_DONE = 3'b101;
reg [2:0] r_SM_Main = s_IDLE;
// The vector that contains the output BCD
reg [DECIMAL_DIGITS*4-1:0] r_BCD = 0;
// The vector that contains the input binary value being shifted.
reg [INPUT_WIDTH-1:0] r_Binary = 0;
// Keeps track of which Decimal Digit we are indexing
reg [DECIMAL_DIGITS-1:0] r_Digit_Index = 0;
// Keeps track of which loop iteration we are on.
// Number of loops performed = INPUT_WIDTH
reg [7:0] r_Loop_Count = 0;
wire [3:0] w_BCD_Digit;
reg r_DV = 1'b0;
always @(posedge i_Clock)
begin
case (r_SM_Main)
// Stay in this state until i_Start comes along
s_IDLE :
begin
r_DV <= 1'b0;
if (i_Start == 1'b1)
begin
r_Binary <= i_Binary;
r_SM_Main <= s_SHIFT;
r_BCD <= 0;
end
else
r_SM_Main <= s_IDLE;
end
// Always shift the BCD Vector until we have shifted all bits through
// Shift the most significant bit of r_Binary into r_BCD lowest bit.
s_SHIFT :
begin
r_BCD <= r_BCD << 1;
r_BCD[0] <= r_Binary[INPUT_WIDTH-1];
r_Binary <= r_Binary << 1;
r_SM_Main <= s_CHECK_SHIFT_INDEX;
end
// Check if we are done with shifting in r_Binary vector
s_CHECK_SHIFT_INDEX :
begin
if (r_Loop_Count == INPUT_WIDTH-1)
begin
r_Loop_Count <= 0;
r_SM_Main <= s_BCD_DONE;
end
else
begin
r_Loop_Count <= r_Loop_Count + 1;
r_SM_Main <= s_ADD;
end
end
// Break down each BCD Digit individually. Check them one-by-one to
// see if they are greater than 4. If they are, increment by 3.
// Put the result back into r_BCD Vector.
s_ADD :
begin
if (w_BCD_Digit > 4)
begin
r_BCD[(r_Digit_Index*4)+:4] <= w_BCD_Digit + 3;
end
r_SM_Main <= s_CHECK_DIGIT_INDEX;
end
// Check if we are done incrementing all of the BCD Digits
s_CHECK_DIGIT_INDEX :
begin
if (r_Digit_Index == DECIMAL_DIGITS-1)
begin
r_Digit_Index <= 0;
r_SM_Main <= s_SHIFT;
end
else
begin
r_Digit_Index <= r_Digit_Index + 1;
r_SM_Main <= s_ADD;
end
end
s_BCD_DONE :
begin
r_DV <= 1'b1;
r_SM_Main <= s_IDLE;
end
default :
r_SM_Main <= s_IDLE;
endcase
end // always @ (posedge i_Clock)
assign w_BCD_Digit = r_BCD[r_Digit_Index*4 +: 4];
assign o_BCD = r_BCD;
assign o_DV = r_DV;
endmodule // Binary_to_BCDAuthors: Tyurin Leonid, Tikhonov Nikita.
Комментарии (5)

ilynxy
03.12.2018 20:14Why this module does exactly 27 iterations?
log2(qbrt(99 999 999)) ~ 8.85 = 9 iterations. The binary search performs on result, not an input value. So 9 iterations is enough, i believe.

ozonar
06.12.2018 14:55А почему статья на английском языке? Это начало той самой экспансии на иностранный рынок, но без какого-либо разделения с русскоязычным Хабром?


Shkaff
Off topic, just out of curiosity: I noticed that there's been a couple of papers in English about the FPGAs from the Innopolis University recently. Is that an initiative from a professor/lecturer? If so, it's a nice one!