В предыдущей части статьи был рассмотрен метод поиска ассоциативных правил в данных европейского социального исследования. Эта часть о статистическом анализе полученных правил. Ключевой момент в том, что классические статистические методы, например, критерий согласия хи-квадрат, не имеют основания быть использованными для результатов опроса. Но по каким причинам? И как проверять гипотезы? Об этом пойдет речь в этой публикации.

Сначала кратко о методах проведения опросов. Одна из характеристик качественного опроса — репрезентативность выборки. Респонденты, отобранные из генеральной совокупности случайным равновероятным образом и без возвращений, определяют простую случайную выборку. По ряду причин получить репрезентативную простую случайную выборку очень затруднительно. Обычно для репрезентативности популяцию делят на страты и для удешевления проведения опроса в каждой страте выделяют кластеры. Кроме того, чтобы получить несмещенную оценку известных показателей популяции (пол, возрастные группы, ...), респондентам, принявшим участие в исследовании, приписывают веса. Подробности можно найти в статье А. Чурикова [1].
Выборка, полученная с использованием стратификации, кластеризации и взвешивания, перестает быть простой случайной. Для переменных такой выборки нарушаются принципы i.i.d., требуемые в классических статистических тестах. В частности, кластеризация выборки, увеличивает статистическую погрешность результатов из-за внутриклассовой корреляции наблюдаемых величин.
Еще один пример отличия от «привычных» формул — нахождение дисперсии для выборочного среднего. Пусть x является численной или логической переменной опроса с весом w. Тогда
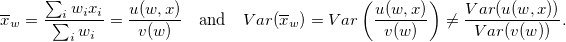
Поэтому отношение функций u/v лианеризуют с помощью ряда Тейлора (ограничиваются разложением до членов первого порядка) и для каждого члена этого ряда находят дисперсию. Этот метод оценки дисперсии выборочного среднего не единственный, есть и другие способы. Подробности, формулы и примеры можно найти в Главе 3, книги [2].
К счастью, в R есть пакет survey, который позволяет производить статистический анализ данных полученных опросами респондентов. Автором этого пакета T. Lumley написано подробное руководство пользователя, изданное в виде книги [3]. Для тех, кто работал с результатами опросов в другом ПО — SAS, Stata, SUDAAN, доступна статья [4]. Кроме того, на web странице поддержки книги [2], для большинства примеров этого издания опубликован код на нескольких языках программирования, в частности и для R.
В данных ESS для каждой страны есть сведения о стратах (stratify), кластерах (psu — primary sample unit) и вероятностях респондентов (prob). Вес, как правило, обратно пропорционален вероятности. Так, для России страты — федеральные округа, кластеры — ряд городов и районов в этих округах. Детали и примеры о дизайне опросов в ESS приводятся в этом pdf, взятом с сайта проекта.
Постановка задачи.
В предыдущей части статьи для одного из найденных правил были получены следующие результаты:

Напомню, здесь Antecedent — левая часть правила X -> Y, означает, что респонденты
— полностью согласны с утверждением, что для большинства жителей страны жизнь становиться скорее хуже, чем лучше
и
— не олицетворяют себя с человеком, для которого важно быть богатым, иметь много денег и дорогие вещи.
Необходимо найти доверительные интервалы для долей X во всех трех странах и показать, что результат поддержки X во Франции значимо отличается от поддержки X в Дании и России.
Подготовка данных.
В полученной базе задаем дизайн исследования
Решение задачи.
Функция svymean( ) пакета survey находит не только выборочное среднее значение, но, в частности, и его стандартное отклонение с учетом дизайна исследования. Тогда доверительный интервал для доли p, равной поддержке X для каждой страны в отдельности, можно найти как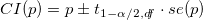 .
.
Добавлю, в survey пакете также доступны биномиальные методы оценки доверительных интервалов долей — функция svyciprop( ).
Для подтверждения значимости отличия долей поддержки X в рассматриваемых странах строим логистическую регрессию вида
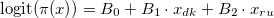
Коэффициенты этой линейной модели означают ровно то же самое, что и в «обычной» логистической регрессии. То есть
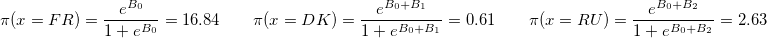
Результаты этой модели показывают, что коэффициенты B_1 и B_2 значимо отличаются от нуля. То есть доля поддержки X во Франции статистически значимо отличается от соответствующих долей в Дании и России.

И, наконец, отвергаем нуль-гипотезу, что оба коэффициента модели — B_1 и B_2, одновременно равны нулю
Так как величины поддержки X в трех рассмотренных странах сильно отличаются, то нуль-гипотезы для коэффициентов логистической регрессии можно было отвергнуть и не используя информацию о дизайне опроса. Я не ставил целью продемонстрировать пример, в котором гипотеза принималась или отвергалась, с некоторым фиксированным уровнем ошибки, в зависимости от того, используем ли мы данные дизайна опроса или нет.
Однако, такие ситуации вполне вероятны. Рассмотрим пример 6.8 из книги [2]: Testing the independence of alcohol dependence and education level in young adults (ages 18–28) using the NCS-R Data, вычисления которого можно полностью воспроизвести использую код R (pdf) с web страницы этой книги.
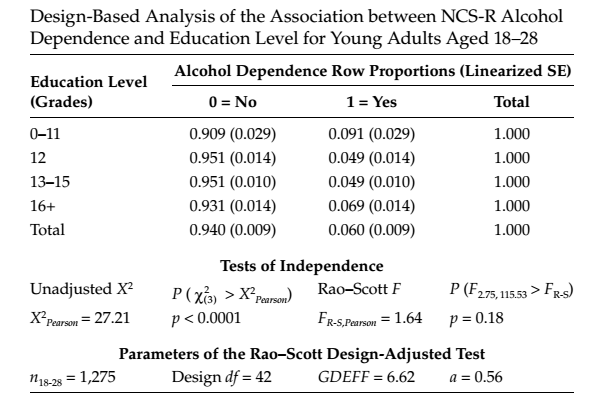
В этом примере проверяется нуль-гипотеза о независимости переменных «диагностирована алкогольная зависимость» и «уровень образования» среди граждан США в возрасте 18-28 лет. Стандартный критерий X^2 отвергает эту гипотезу с вероятностью ошибки менее 1 %, то есть уверенно можем говорить о наличии зависимости между этими переменными в указанной популяции. Тогда как хи-квадрат тест, с поправкой Рао-Скотта на дизайн исследования, определяет величину ошибочного отклонения нуль-гипотезы более чем в 10%. Получается, что отвергнуть нуль-гипотезу на 5% уровне уже невозможно.
Поэтому, в общем случае, статистический анализ результатов опросов желательно проводить с учетом дизайна исследований.
В завершение отмечу, что в последнее время для анализа межстрановых результатов стали использовать моделирование структурными уравнениями. Одна из причин этого в том, что стратификация и кластеризация выборки обычно производится на уровне страны (в ESS именно так), а не в общей популяции. Но об этом когда-нибудь позднее, пока упомяну сборник статей [5].
Литература:
[1] Чуриков А. Случайные и неслучайные выборки в социологических исследованиях, ж. Социальная реальность, 4, 2007, стр. 89-109.
[2] Heeringa S.G., West B.T., Berglund P.A. Applied Survey Data Analysis, CRC Press, 2010.
[3] Lumley T. Complex Surveys: A Guide to Analysis Using R, Wiley, 2010.
[4] Damico A. Transitioning to R: Replicating SAS, Stata, and SUDAAN Analysis Techniques in Health Policy Data, The R Journal Vol. 1/2, December 2009.
[5] Cross-Cultural Analysis: Methods and Applications (edited by Davidov E., Schmidt P., Billiet J.), Routledge, 2011.

Сначала кратко о методах проведения опросов. Одна из характеристик качественного опроса — репрезентативность выборки. Респонденты, отобранные из генеральной совокупности случайным равновероятным образом и без возвращений, определяют простую случайную выборку. По ряду причин получить репрезентативную простую случайную выборку очень затруднительно. Обычно для репрезентативности популяцию делят на страты и для удешевления проведения опроса в каждой страте выделяют кластеры. Кроме того, чтобы получить несмещенную оценку известных показателей популяции (пол, возрастные группы, ...), респондентам, принявшим участие в исследовании, приписывают веса. Подробности можно найти в статье А. Чурикова [1].
Выборка, полученная с использованием стратификации, кластеризации и взвешивания, перестает быть простой случайной. Для переменных такой выборки нарушаются принципы i.i.d., требуемые в классических статистических тестах. В частности, кластеризация выборки, увеличивает статистическую погрешность результатов из-за внутриклассовой корреляции наблюдаемых величин.
Еще один пример отличия от «привычных» формул — нахождение дисперсии для выборочного среднего. Пусть x является численной или логической переменной опроса с весом w. Тогда
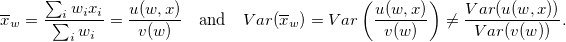
Поэтому отношение функций u/v лианеризуют с помощью ряда Тейлора (ограничиваются разложением до членов первого порядка) и для каждого члена этого ряда находят дисперсию. Этот метод оценки дисперсии выборочного среднего не единственный, есть и другие способы. Подробности, формулы и примеры можно найти в Главе 3, книги [2].
К счастью, в R есть пакет survey, который позволяет производить статистический анализ данных полученных опросами респондентов. Автором этого пакета T. Lumley написано подробное руководство пользователя, изданное в виде книги [3]. Для тех, кто работал с результатами опросов в другом ПО — SAS, Stata, SUDAAN, доступна статья [4]. Кроме того, на web странице поддержки книги [2], для большинства примеров этого издания опубликован код на нескольких языках программирования, в частности и для R.
В данных ESS для каждой страны есть сведения о стратах (stratify), кластерах (psu — primary sample unit) и вероятностях респондентов (prob). Вес, как правило, обратно пропорционален вероятности. Так, для России страты — федеральные округа, кластеры — ряд городов и районов в этих округах. Детали и примеры о дизайне опросов в ESS приводятся в этом pdf, взятом с сайта проекта.
Постановка задачи.
В предыдущей части статьи для одного из найденных правил были получены следующие результаты:

Напомню, здесь Antecedent — левая часть правила X -> Y, означает, что респонденты
— полностью согласны с утверждением, что для большинства жителей страны жизнь становиться скорее хуже, чем лучше
и
— не олицетворяют себя с человеком, для которого важно быть богатым, иметь много денег и дорогие вещи.
Необходимо найти доверительные интервалы для долей X во всех трех странах и показать, что результат поддержки X во Франции значимо отличается от поддержки X в Дании и России.
Подготовка данных.
Загружаем в R данные ESS 6 волны (редакция 2.1) и информацию о дизайне опросов
Данные выложены в открытый доступ, но для их загрузки необходима регистрация. После авторизации скачиваем отсюда stata данные в рабочую директорию R.
#Danish survey design data
# French survey design data
#Russian survey design data
library(foreign) # to read data
library(data.table) # to manipulate data
srv.data <- read.dta("ESS6e02_1.dta")
srv.variables <- data.table(name = names(srv.data), title = attr(srv.data, "var.labels"))
srv.data <- data.table(srv.data)
setkey(srv.data, cntry)
setkey(srv.variables, name)
#Danish survey design data
dk.dt <- data.table(read.dta("ESS6_DK_SDDF.dta"))
dk.dt <- dk.dt[cntry!="NA",] # sic! this base contains extra records with NA data
dk.dt[,stratify:="dk"] # dk sample is simple random sample
dk.dt[,psu:=seq(3300,length.out = nrow(dk.dt))] #to avoid duplication with psu numbers of the fr data
# French survey design data
fr.dt <- data.table(read.dta("ESS6_FR_SDDF.dta"))
#Russian survey design data
ru.dt <- data.table(read.dta("ESS6_RU_SDDF.dta"))
Формируем требуемую базу данных и добавляем в нее переменную с поддержкой утверждения X
countries.set <- c("FR", "DK", "RU")
cntries.srv.data <- srv.data[J(countries.set)]
setkey(cntries.srv.data, cntry, idno) # idno is unique respondent's ID inside cntry
cntries.dt <- rbind(dk.dt, fr.dt, ru.dt)
setkey(cntries.dt, cntry,idno)
cntries.srv.data <- cntries.srv.data[cntries.dt] # merge the databases
cntries.srv.data[,weight:=dweight*pweight] # weight is defined as design weight adjusted on the countries population sizes
# add antecedent (denoted as lhs) statement to the cntries.srv.data
lhs.rule.adding<-function(lhs){
statements <- unlist(strsplit(lhs, " & "))
statements <- lapply(statements, function(l) unlist(strsplit(l,"=")))
statements <- lapply( statements, function(l)
c(question.name=srv.variables[title==l[1], name], answer=l[2]) )
conditions <- sapply( statements, function(l)
paste("ifelse(is.na(", l[1], "), 0, ", l[1], " == '", l[2], "')", sep="") )
conditions <- paste(conditions, collapse = " & ")
add.lhs.to.base <- paste("cntries.srv.data[,x:=", conditions,"]",sep="")
eval(parse(text=add.lhs.to.base))
cntries.srv.data[,x:=as.numeric(x)]
return(T)
}
lhs.rule.adding("For most people in country life is getting worse=Agree strongly & Important to be rich, have money and expensive things=Not like me")
cntries.srv.data[,cntry:=factor(cntry, levels = countries.set)]
В полученной базе задаем дизайн исследования
library(survey)
design.cntries.data <- svydesign(ids = ~psu, strata = ~stratify, weights = ~weight, data = cntries.srv.data)
Решение задачи.
Функция svymean( ) пакета survey находит не только выборочное среднее значение, но, в частности, и его стандартное отклонение с учетом дизайна исследования. Тогда доверительный интервал для доли p, равной поддержке X для каждой страны в отдельности, можно найти как
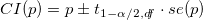 .
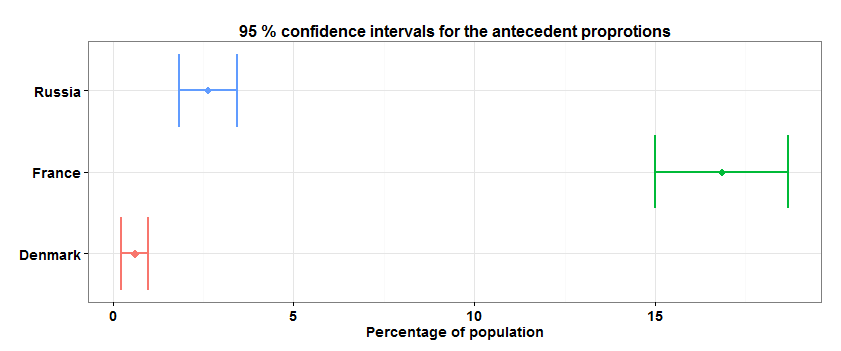
.Код R для нахождения доверительных интервалов и построения графика
X.supp.confint <- sapply(countries.set, function(country) {
design.dt<-subset(design.cntries.data, cntry==country)
w.mean<-svymean(~x, design.dt)
c(w.mean[1],confint(w.mean,df = degf(design.dt))[1,])
})
X.supp.confint <- data.table(t(X.supp.confint)*100, country=c("France", "Denmark", "Russia"))
setnames(X.supp.confint, 1:3, c("mean","lower","upper"))
library(ggplot2)
limits <- aes(xmax = upper, xmin=lower)
p <- ggplot(X.supp.confint, aes(y=country, x=mean, colour=country)) +
geom_point(size=4, shape=18) + geom_errorbarh(limits, width=0.2, lwd=1.0)
p <- p + ggtitle("95 % confidence intervals for the antecedent proprotions") + xlab("Percentage of population")
p + theme_bw() + theme(plot.title=element_text( face="bold", size=16),
axis.text.y = element_text( face="bold", size=14),
axis.text.x = element_text( face="bold", size=14),
axis.title.x=element_text( face="bold", size=14),
axis.title.y=element_blank(), legend.position="none")

Добавлю, в survey пакете также доступны биномиальные методы оценки доверительных интервалов долей — функция svyciprop( ).
Для подтверждения значимости отличия долей поддержки X в рассматриваемых странах строим логистическую регрессию вида
model <- svyglm(x~ cntry, design = design.cntries.data, family=quasibinomial)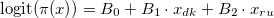
Коэффициенты этой линейной модели означают ровно то же самое, что и в «обычной» логистической регрессии. То есть
sapply(c(coef(model)[1], sum(coef(model)[c(1,2)]), sum(coef(model)[c(1,3)])), function(b) exp(b)/(1+exp(b)))*100 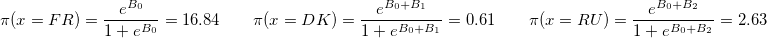
Результаты этой модели показывают, что коэффициенты B_1 и B_2 значимо отличаются от нуля. То есть доля поддержки X во Франции статистически значимо отличается от соответствующих долей в Дании и России.
library(DT); datatable(round(coef(summary(model)),4)) 
И, наконец, отвергаем нуль-гипотезу, что оба коэффициента модели — B_1 и B_2, одновременно равны нулю
regTermTest(model, ~cntry, method = "LRT")
Working (Rao-Scott+F) LRT for cntry
in svyglm(formula = x ~ cntry, design = design.cntries.data, family = quasibinomial)
Working 2logLR = 379.0228 p= < 2.22e-16
(scale factors: 1.2 0.8 ); denominator df= 2088
Так как величины поддержки X в трех рассмотренных странах сильно отличаются, то нуль-гипотезы для коэффициентов логистической регрессии можно было отвергнуть и не используя информацию о дизайне опроса. Я не ставил целью продемонстрировать пример, в котором гипотеза принималась или отвергалась, с некоторым фиксированным уровнем ошибки, в зависимости от того, используем ли мы данные дизайна опроса или нет.
Однако, такие ситуации вполне вероятны. Рассмотрим пример 6.8 из книги [2]: Testing the independence of alcohol dependence and education level in young adults (ages 18–28) using the NCS-R Data, вычисления которого можно полностью воспроизвести использую код R (pdf) с web страницы этой книги.

В этом примере проверяется нуль-гипотеза о независимости переменных «диагностирована алкогольная зависимость» и «уровень образования» среди граждан США в возрасте 18-28 лет. Стандартный критерий X^2 отвергает эту гипотезу с вероятностью ошибки менее 1 %, то есть уверенно можем говорить о наличии зависимости между этими переменными в указанной популяции. Тогда как хи-квадрат тест, с поправкой Рао-Скотта на дизайн исследования, определяет величину ошибочного отклонения нуль-гипотезы более чем в 10%. Получается, что отвергнуть нуль-гипотезу на 5% уровне уже невозможно.
Поэтому, в общем случае, статистический анализ результатов опросов желательно проводить с учетом дизайна исследований.
В завершение отмечу, что в последнее время для анализа межстрановых результатов стали использовать моделирование структурными уравнениями. Одна из причин этого в том, что стратификация и кластеризация выборки обычно производится на уровне страны (в ESS именно так), а не в общей популяции. Но об этом когда-нибудь позднее, пока упомяну сборник статей [5].
Литература:
[1] Чуриков А. Случайные и неслучайные выборки в социологических исследованиях, ж. Социальная реальность, 4, 2007, стр. 89-109.
[2] Heeringa S.G., West B.T., Berglund P.A. Applied Survey Data Analysis, CRC Press, 2010.
[3] Lumley T. Complex Surveys: A Guide to Analysis Using R, Wiley, 2010.
[4] Damico A. Transitioning to R: Replicating SAS, Stata, and SUDAAN Analysis Techniques in Health Policy Data, The R Journal Vol. 1/2, December 2009.
[5] Cross-Cultural Analysis: Methods and Applications (edited by Davidov E., Schmidt P., Billiet J.), Routledge, 2011.

