Хотя меши являются простейшим и наиболее универсальным способом рендеринга, существуют и другие варианты представления фигур в 2d и 3d. Одним из часто используемых способов являются поля расстояний со знаком (signed distance fields, SDF). Поля расстояний со знаком обеспечивают менее затратную трассировку лучей, позволяют разным фигурам плавно перетекать друг в друга и экономить на текстурах низкого разрешения для высококачественных изображений.
Мы начнём с генерации полей расстояний со знаком с помощью функций в двух измерениях, но позже продолжим генерировать их в 3D. Я буду использовать координаты мирового пространства, чтобы у нас была как можно меньшая зависимости от масштабирования и UV-координат, поэтому если вы не понимаете, как это работает, то изучите этот туториал по плоскому наложению, в котором объяснено, что происходит.
Мы временно выбросим свойства из базового шейдера плоского наложения, потому что пока займёмся технической основой. Затем мы запишем позицию вершины в мире непосредственно во фрагментную структуру, а не будем сначала преобразовывать её в UV. На последнем этапе подготовки мы напишем новую функцию, которая вычисляет сцену и возвращает расстояние до ближайшей поверхности. Затем мы вызовем функции и используем результат в качестве цвета.
Я буду писать все функции для полей расстояний со знаком в отдельном файле, чтобы мы могли использовать их многократно. Для этого я создам новый файл. В него мы добавим зли нет, то мы задаём её и завершаем условные ащиту include, проверяя сначала, задана ли переменная препроцессора. Если она ещё не задана, то мы задаём её и завершаем условную конструкцию if после функций, которые мы хотим включить. Преимущество этого в том, что если мы добавим файл дважды (например, если мы добавим два разных файла, в каждом из которых есть нужные нам функции, и они оба добавляют одинаковый файл), то это сломает шейдер. Если вы уверены, что такого никогда не произойдёт, то можно эту проверку не выполнять.
Если файл include находится одной папке с основным шейдером, мы можем просто включить его с помощью конструкции pragma.
Так мы увидим только чёрную поверхность на отрендеренной поверхности, готовую к отображению на ней расстояния со знаком.

Простейшая функция поля расстояний со знаком — это функция круга. Функция будет получать только позицию сэмпла и радиус окружности. Начнём мы с получения длины вектора позиции сэмпла. Так мы получим точку в позиции (0, 0), что аналогично кругу с радиусом 0.
Затем можно вызвать функцию круга в функции сцены и вернуть возвращаемое ею расстояние.

Затем мы добавим в вычисления радиус. Важный аспект функций расстояний со знаком заключается в том, что когда мы находимся внутри объекта, то получаем отрицательное расстояние до поверхности (именно это обозначает слово signed в выражении signed distance field). Чтобы увеличить окружность до радиуса, мы просто вычитаем радиус из длины. Таким образом поверхность, которая находится везде, где функция возвращает 0, движется наружу. То, что находится в двух единицах расстояния от поверхности для круга с размером 0, находится всего в одной единице от круга с радиусом 1, и на одну единицу внутри круга (значение равно -1) для круга с радиусом 3;

Теперь единственное, что мы не можем сделать — это сдвинуть окружность от центра. Чтобы исправить это, можно добавить к функции окружности новый аргумент для вычисления расстояния между позицией сэмпла и центром окружности, и вычесть из этого значения радиус, чтобы задать круг. Или можно переопределить точку начала координат, переместив пространство точки сэмпла, а затем получить окружность в этом пространстве. Второй вариант выглядит гораздо сложнее, но поскольку перемещение объектов — это операция, которую мы хотим использовать для всех фигур, он намного универсальнее, а поэтому его я и буду объяснять.
«Преобразование пространства точки» — звучит гораздо страшнее, чем есть на самом деле. Это означает, что мы передаём точку в функцию, а функция изменяет её так, чтобы мы могли по-прежнему использовать её в дальнейшем. В случае переноса мы просто вычитаем смещение из точки. Позиция вычитается, когда мы хотим переместить фигуры в положительном направлении, потому что фигуры, которые мы рендерим в пространстве, перемещаются в направлении, противоположном перемещению пространства.
Например, если мы хотим отрисовать сферу в позиции

Ещё одна простая фигура — это прямоугольник. Начнём с того, что рассмотрим компоненты по отдельности. Сначала мы получаем расстояние от центра, взяв абсолютное значение. Затем аналогично кругу, мы вычитаем половину размера (которое по сути похоже на радиус прямоугольника). Чтобы просто показать, как будут выглядеть результаты, мы пока вернём только один компонент.

Теперь мы можем получить дешёвую версию прямоугольника, просто вернув наибольший компонент 2. Это работает во многих случаях, но не правильно, потому что не отображает правильное расстояние вокруг углов.

Правильные значения для прямоугольника за пределами фигуры можно получить, взяв сначала максимум между расстояниями до рёбер и 0, а затем взяв его длину.
Если мы не будем ограничивать расстояние снизу значением 0, то просто вычислим расстояние до углов (где edgeDistances равны
Чтобы исправить расстояние 0 для всей внутренней части, нужно сгенерировать внутреннее расстояние, просто воспользовавшись формулой дешёвого прямоугольника (взяв максимальное значение из компонента x и y), а затем гарантировав, что оно никогда не будет превышать 0, взяв минимальное значение от него до 0. Затем мы складываем внешнее расстояние, которое никогда не бывает ниже 0, и внутреннее расстояние, которое никогда не превышает 0 и получаем готовую функцию расстояний.
Так как ранее мы записали функцию переноса в универсальном виде, то теперь можно также воспользоваться ею, чтобы переместить его центр в любое место.

Поворот фигур выполняется аналогично перемещению. Перед вычислением расстояния до фигуры мы поворачиваем координаты в противоположном направлении. Чтобы максимально упростить понимание поворотов, мы умножим поворот на 2 * pi, чтобы получить угол в радианах. Таким образом, мы передаём в функцию поворот, где 0.25 — это четверть поворота, 0.5 — половина поворота, а 1 — полный поворот (можете выполнять преобразования иначе, если вам так покажется естественнее). Также мы инвертируем поворот, потому что нужно поворачивать позицию в противоположном от поворота фигуры направлении по той же причине, что и при перемещении.
Для вычисления повёрнутых координат мы сначала вычислим синус и косинус на основании угла. В Hlsl есть функция sincos, вычисляющая оба эти значения быстрее, чем при вычислении по отдельности.
При построении нового вектора для компонента x мы берём исходный компонент x, умноженный на косинус, и компонент y, умноженный на синус. Это можно легко запомнить, если помнить, что косинус 0 равен 1, а при повороте на 0 мы хотим, чтобы компонент x нового вектора был точно таким же, как раньше (то есть умножаем на 1). Компонента y, которая ранее указывала вверх, не вносила никакого вклада в компонент x, поворачивается вправо, и её значения начинаются с 0, поначалу становясь больше, то есть её движение полностью описывается синусом.
Для компонента y нового вектора мы умножаем косинус на компонент y старого вектора и вычитаем синус, умноженный на старый компонент x. Чтобы понять, почему мы вычитаем, а не прибавляем синус, умноженный на компонент x, лучше всего представить, как меняется вектор
Теперь, когда мы написали способ поворота, можно использовать его в сочетании с переносом, чтобы перемещать и вращать фигуру.

В этом случае мы сначала поворачиваем объект вокруг центра всей сцены, чтобы поворот повлиял и на перенос. Чтобы повернуть фигуру относительно её собственного центра, сначала нужно переместить её, а затем повернуть. Благодаря этому изменённому порядку ко времени поворота центр фигуры станет центром системы координат.

Масштабирование работает аналогично другим способам преобразования фигур. Мы делим координаты на масштаб, отрисовывая фигуру в пространстве с уменьшенным масштабом, и в базовой системе координат они становятся больше.

Хотя это выполняет масштабирование правильно, расстояние тоже масштабируется. Основное преимущество поля расстояний со знаком заключается в том, что мы всегда знаем расстояние до ближайшей поверхности, но изменение масштаба полностью уничтожает данное свойство. Это можно легко исправить, умножив поле расстояний, полученное от функции расстояния со знаком (в нашем случае

Поля расстояний со знаком можно использовать для разных вещей, например, создания теней, рендеринга 3D-сцен, физики и рендеринга текста. Но мы пока не хотим углубляться в сложности, поэтому я объясню только две техники их визуализации. Первая — чёткая форма со сглаживанием (antialiasing), вторая — рендеринг линий в зависимости от расстояния.
Этот метод схож с тем, который часто используется при рендеринге текста, он создаёт чёткую форму. Если мы хотим генерировать поле расстояний не из функции, а будем считывать её из текстуры, то это позволяет нам использовать текстуры с гораздо меньшим разрешением, чем обычно, и получать хорошие результаты. TextMesh Pro использует эту технику для рендеринга текста.
Для применения этой техники мы пользуемся тем фактом, что данные в полях расстояний со знаком, и нам известна точка отсечки. Мы начинаем с вычисления того, насколько поле расстояний изменяется к следующему пикселю. Это должна быть та же величина, что и длина изменения координат, но проще и надёжнее вычислять расстояние со знаком.
Получив изменение расстояния, мы можем сделать smoothstep с половины изменения расстояния до минус/плюс половины изменения расстояния. Это выполнит простую отсечку примерно около 0, но со сглаживанием. Затем можно использовать это сглаженное значение для любого нужного нам двоичного значения. В этом примере я сменю шейдер на шейдер прозрачности и использую его для альфа-канала. Я делаю smoothstep с положительного на отрицательное значение потому, что мы хотим, чтобы было видимым отрицательное значение поля расстояний. Если вы не совсем понимаете, как здесь работает рендеринг прозрачности, то рекомендую прочитать мой туториал по рендерингу прозрачности.

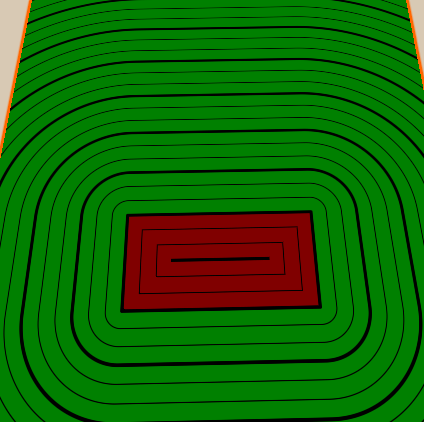
Ещё одна распространённая техника визуализации полей расстояний заключается в отображении расстояний в виде линий. В нашей реализации я добавлю несколько толстых линий и несколько тонких между ними. Также я раскрашу внутреннюю и наружную части фигуры в разные цвета, чтобы было видно, где находится объект.
Мы начнём с отображения разницы между внутренней и внешней частями фигуры. Цвета можно будет настраивать в материале, поэтому мы добавим новые свойства, а также переменные шейдера для внутреннего и внешнего цветов фигуры.
Затем во фрагментном шейдере мы проверяем, где находится пиксель, который мы рендерим, сравнивая расстояние со знаком с 0 при помощи функции

Чтобы отрендерить линии, нам сначала нужно указать, как часто мы будем рендерить линии, и насколько толстыми они будут, задав свойства и соответствующие переменные шейдера.
Затем для рендеринга линий мы начнём с вычисления изменения расстояния, чтобы в дальнейшем использовать его для сглаживания. Также мы уже поделили его на 2, потому что позже мы прибавим его половину и вычтем его половину, чтобы покрыть расстояние изменения в 1 пиксель.
Затем мы берём расстояние и преобразовываем его таким образом, чтобы оно имело одинаковое поведение в повторяющихся точках. Для этого мы сначала разделим его на расстояние между линиями, при этом у нас не получатся полные числа на каждом первом шаге, а полные числа только на основании заданного нами расстояния.
Затем мы прибавляем к числу 0.5, берём дробную часть и снова вычитаем 0.5. Дробная часть и вычитание нужны здесь для того, чтобы линия проходила через ноль в повторяющемся паттерне. Прибавляем мы 0.5 до получения дробной части для того, чтобы нейтрализовать дальнейшее вычитание 0.5 — смещение приведёт к тому, что значения, при которых график равен 0, находятся в 0, 1, 2 и т.д., а не в 0.5, 1.5, и т.д.
Последние шаги для преобразования значения — мы берём абсолютное значение и снова умножаем его на расстояние между линиями. Абсолютное значение делает так, что области до и после точек линии остаются такими же, что упрощает создание отсечки для линий. Последняя операция, в которой мы снова умножаем значение на расстояние между линиями, нужна, чтобы нейтрализовать деление в начале уравнения, благодаря нему изменение в значении снова такое же, как в начале, а вычисленное нами ранее изменение расстояния по-прежнему является верным.

Теперь, когда мы вычислили расстояние до линий на основании расстояния до фигуры, можно отрисовать линии. Мы выполняем smoothstep от linethickness минус половина изменения расстояния до linethickness плюс половина изменения расстояния и используем только что вычисленное расстояние линии в качестве значения для сравнения. После вычисления этого значения мы умножаем его на цвет, чтобы создать чёрные линии (можно также выполнить lerp до другого цвета, если вам нужны разноцветные линии).
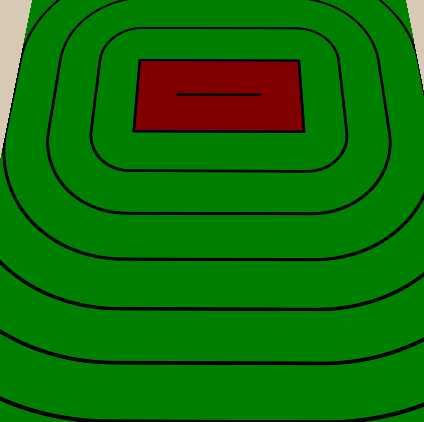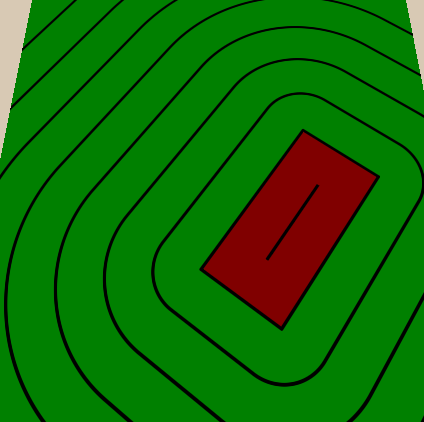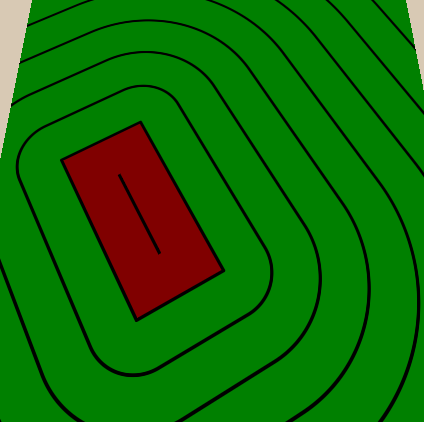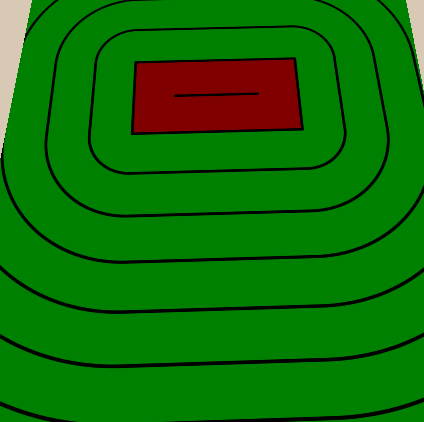
Тонкие линии между толстыми мы реализуем аналогичным образом — добавляем свойство, определяющее, сколько тонких линий должно быть между толстыми, а потом делаем то же, что делали с толстыми, но из-за расстояния между тонкими линиями делим расстояние между толстыми на количество тонких линий между ними. Также мы сделаем количество тонких линий
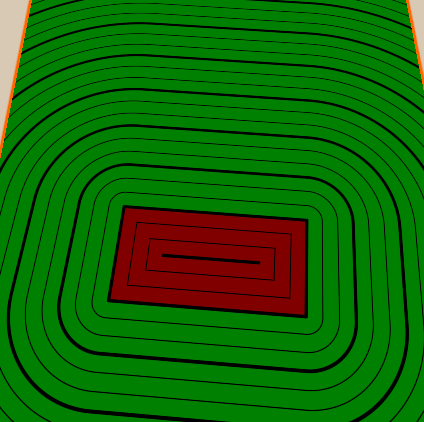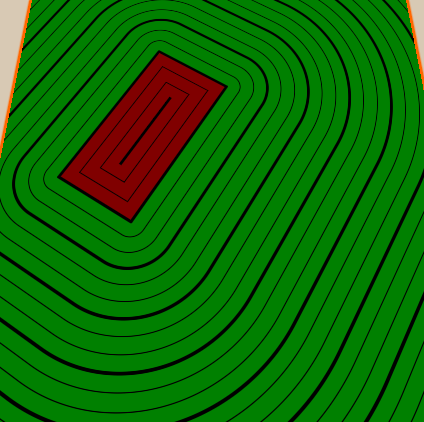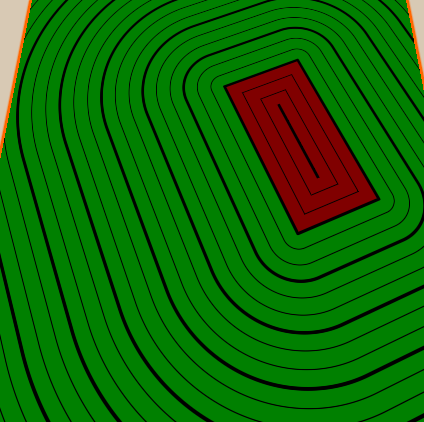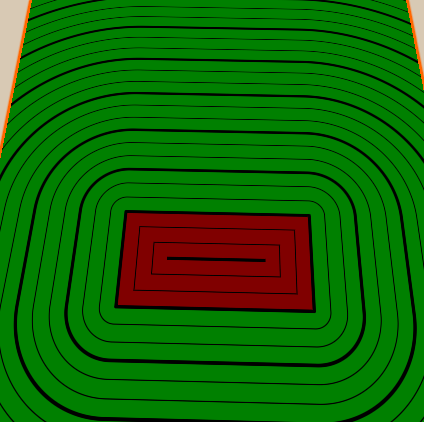
Надеюсь, мне удалось объяснить основы полей расстояний со знаком, и вы уже ждёте несколько новых туториалов, в которых я расскажу о других способах их применения.
Мы начнём с генерации полей расстояний со знаком с помощью функций в двух измерениях, но позже продолжим генерировать их в 3D. Я буду использовать координаты мирового пространства, чтобы у нас была как можно меньшая зависимости от масштабирования и UV-координат, поэтому если вы не понимаете, как это работает, то изучите этот туториал по плоскому наложению, в котором объяснено, что происходит.

Подготовка основы
Мы временно выбросим свойства из базового шейдера плоского наложения, потому что пока займёмся технической основой. Затем мы запишем позицию вершины в мире непосредственно во фрагментную структуру, а не будем сначала преобразовывать её в UV. На последнем этапе подготовки мы напишем новую функцию, которая вычисляет сцену и возвращает расстояние до ближайшей поверхности. Затем мы вызовем функции и используем результат в качестве цвета.
Shader "Tutorial/034_2D_SDF_Basics"{
SubShader{
//материал полностью непрозрачен и рендерится одновременно со всей другой непрозрачной геометрией
Tags{ "RenderType"="Opaque" "Queue"="Geometry"}
Pass{
CGPROGRAM
#include "UnityCG.cginc"
#pragma vertex vert
#pragma fragment frag
struct appdata{
float4 vertex : POSITION;
};
struct v2f{
float4 position : SV_POSITION;
float4 worldPos : TEXCOORD0;
};
v2f vert(appdata v){
v2f o;
//вычисляем позицию в пространстве усечённых координат для рендеринга объекта
o.position = UnityObjectToClipPos(v.vertex);
//вычисляем позицию вершины в мире
o.worldPos = mul(unity_ObjectToWorld, v.vertex);
return o;
}
float scene(float2 position) {
// вычисляем расстояние до ближайшей поверхности
return 0;
}
fixed4 frag(v2f i) : SV_TARGET{
float dist = scene(i.worldPos.xz);
fixed4 col = fixed4(dist, dist, dist, 1);
return col;
}
ENDCG
}
}
FallBack "Standard" //fallback добавляет проход тени, чтобы создавать тени на других объектах
}Я буду писать все функции для полей расстояний со знаком в отдельном файле, чтобы мы могли использовать их многократно. Для этого я создам новый файл. В него мы добавим зли нет, то мы задаём её и завершаем условные ащиту include, проверяя сначала, задана ли переменная препроцессора. Если она ещё не задана, то мы задаём её и завершаем условную конструкцию if после функций, которые мы хотим включить. Преимущество этого в том, что если мы добавим файл дважды (например, если мы добавим два разных файла, в каждом из которых есть нужные нам функции, и они оба добавляют одинаковый файл), то это сломает шейдер. Если вы уверены, что такого никогда не произойдёт, то можно эту проверку не выполнять.
// in include file
// include guards that keep the functions from being included more than once
#ifndef SDF_2D
#define SDF_2D
// functions
#endifЕсли файл include находится одной папке с основным шейдером, мы можем просто включить его с помощью конструкции pragma.
// in main shader
#include "2D_SDF.cginc"Так мы увидим только чёрную поверхность на отрендеренной поверхности, готовую к отображению на ней расстояния со знаком.

Круг
Простейшая функция поля расстояний со знаком — это функция круга. Функция будет получать только позицию сэмпла и радиус окружности. Начнём мы с получения длины вектора позиции сэмпла. Так мы получим точку в позиции (0, 0), что аналогично кругу с радиусом 0.
float circle(float2 samplePosition, float radius){
return length(samplePosition);
}Затем можно вызвать функцию круга в функции сцены и вернуть возвращаемое ею расстояние.
float scene(float2 position) {
float sceneDistance = circle(position, 2);
return sceneDistance;
}
Затем мы добавим в вычисления радиус. Важный аспект функций расстояний со знаком заключается в том, что когда мы находимся внутри объекта, то получаем отрицательное расстояние до поверхности (именно это обозначает слово signed в выражении signed distance field). Чтобы увеличить окружность до радиуса, мы просто вычитаем радиус из длины. Таким образом поверхность, которая находится везде, где функция возвращает 0, движется наружу. То, что находится в двух единицах расстояния от поверхности для круга с размером 0, находится всего в одной единице от круга с радиусом 1, и на одну единицу внутри круга (значение равно -1) для круга с радиусом 3;
float circle(float2 samplePosition, float radius){
return length(samplePosition) - radius;
}
Теперь единственное, что мы не можем сделать — это сдвинуть окружность от центра. Чтобы исправить это, можно добавить к функции окружности новый аргумент для вычисления расстояния между позицией сэмпла и центром окружности, и вычесть из этого значения радиус, чтобы задать круг. Или можно переопределить точку начала координат, переместив пространство точки сэмпла, а затем получить окружность в этом пространстве. Второй вариант выглядит гораздо сложнее, но поскольку перемещение объектов — это операция, которую мы хотим использовать для всех фигур, он намного универсальнее, а поэтому его я и буду объяснять.
Перемещение
«Преобразование пространства точки» — звучит гораздо страшнее, чем есть на самом деле. Это означает, что мы передаём точку в функцию, а функция изменяет её так, чтобы мы могли по-прежнему использовать её в дальнейшем. В случае переноса мы просто вычитаем смещение из точки. Позиция вычитается, когда мы хотим переместить фигуры в положительном направлении, потому что фигуры, которые мы рендерим в пространстве, перемещаются в направлении, противоположном перемещению пространства.
Например, если мы хотим отрисовать сферу в позиции
(3, 4), то нужно изменить пространство так, чтобы (3, 4) превратились в (0, 0), и для этого нужно вычесть (3, 4). Теперь если мы отрисуем сферу вокруг новой точки начала координат, то она будет старой точкой (3, 4).// in sdf functions include file
float2 translate(float2 samplePosition, float2 offset){
return samplePosition - offset;
}float scene(float2 position) {
float2 circlePosition = translate(position, float2(3, 2));
float sceneDistance = circle(circlePosition, 2);
return sceneDistance;
}
Прямоугольник
Ещё одна простая фигура — это прямоугольник. Начнём с того, что рассмотрим компоненты по отдельности. Сначала мы получаем расстояние от центра, взяв абсолютное значение. Затем аналогично кругу, мы вычитаем половину размера (которое по сути похоже на радиус прямоугольника). Чтобы просто показать, как будут выглядеть результаты, мы пока вернём только один компонент.
float rectangle(float2 samplePosition, float2 halfSize){
float2 componentWiseEdgeDistance = abs(samplePosition) - halfSize;
return componentWiseEdgeDistance.x;
}
Теперь мы можем получить дешёвую версию прямоугольника, просто вернув наибольший компонент 2. Это работает во многих случаях, но не правильно, потому что не отображает правильное расстояние вокруг углов.

Правильные значения для прямоугольника за пределами фигуры можно получить, взяв сначала максимум между расстояниями до рёбер и 0, а затем взяв его длину.
Если мы не будем ограничивать расстояние снизу значением 0, то просто вычислим расстояние до углов (где edgeDistances равны
(0, 0)), но при этом координаты между углами не будут опускаться ниже 0, поэтому будет использоваться всё ребро. Недостаток этого в том, что 0 используется как расстояние от ребра для всей внутренней части фигуры.Чтобы исправить расстояние 0 для всей внутренней части, нужно сгенерировать внутреннее расстояние, просто воспользовавшись формулой дешёвого прямоугольника (взяв максимальное значение из компонента x и y), а затем гарантировав, что оно никогда не будет превышать 0, взяв минимальное значение от него до 0. Затем мы складываем внешнее расстояние, которое никогда не бывает ниже 0, и внутреннее расстояние, которое никогда не превышает 0 и получаем готовую функцию расстояний.
float rectangle(float2 samplePosition, float2 halfSize){
float2 componentWiseEdgeDistance = abs(samplePosition) - halfSize;
float outsideDistance = length(max(componentWiseEdgeDistance, 0));
float insideDistance = min(max(componentWiseEdgeDistance.x, componentWiseEdgeDistance.y), 0);
return outsideDistance + insideDistance;
}Так как ранее мы записали функцию переноса в универсальном виде, то теперь можно также воспользоваться ею, чтобы переместить его центр в любое место.
float scene(float2 position) {
float2 circlePosition = translate(position, float2(1, 0));
float sceneDistance = rectangle(circlePosition, float2(1, 2));
return sceneDistance;
}
Поворот
Поворот фигур выполняется аналогично перемещению. Перед вычислением расстояния до фигуры мы поворачиваем координаты в противоположном направлении. Чтобы максимально упростить понимание поворотов, мы умножим поворот на 2 * pi, чтобы получить угол в радианах. Таким образом, мы передаём в функцию поворот, где 0.25 — это четверть поворота, 0.5 — половина поворота, а 1 — полный поворот (можете выполнять преобразования иначе, если вам так покажется естественнее). Также мы инвертируем поворот, потому что нужно поворачивать позицию в противоположном от поворота фигуры направлении по той же причине, что и при перемещении.
Для вычисления повёрнутых координат мы сначала вычислим синус и косинус на основании угла. В Hlsl есть функция sincos, вычисляющая оба эти значения быстрее, чем при вычислении по отдельности.
При построении нового вектора для компонента x мы берём исходный компонент x, умноженный на косинус, и компонент y, умноженный на синус. Это можно легко запомнить, если помнить, что косинус 0 равен 1, а при повороте на 0 мы хотим, чтобы компонент x нового вектора был точно таким же, как раньше (то есть умножаем на 1). Компонента y, которая ранее указывала вверх, не вносила никакого вклада в компонент x, поворачивается вправо, и её значения начинаются с 0, поначалу становясь больше, то есть её движение полностью описывается синусом.
Для компонента y нового вектора мы умножаем косинус на компонент y старого вектора и вычитаем синус, умноженный на старый компонент x. Чтобы понять, почему мы вычитаем, а не прибавляем синус, умноженный на компонент x, лучше всего представить, как меняется вектор
(1, 0) при повороте по часовой стрелке. Компонент y результата начинается с 0, а затем становится меньше 0. Это противоположно тому, как ведёт себя синус, поэтому мы меняем знак.float2 rotate(float2 samplePosition, float rotation){
const float PI = 3.14159;
float angle = rotation * PI * 2 * -1;
float sine, cosine;
sincos(angle, sine, cosine);
return float2(cosine * samplePosition.x + sine * samplePosition.y, cosine * samplePosition.y - sine * samplePosition.x);
}Теперь, когда мы написали способ поворота, можно использовать его в сочетании с переносом, чтобы перемещать и вращать фигуру.
float scene(float2 position) {
float2 circlePosition = position;
circlePosition = rotate(circlePosition, _Time.y);
circlePosition = translate(circlePosition, float2(2, 0));
float sceneDistance = rectangle(circlePosition, float2(1, 2));
return sceneDistance;
}
В этом случае мы сначала поворачиваем объект вокруг центра всей сцены, чтобы поворот повлиял и на перенос. Чтобы повернуть фигуру относительно её собственного центра, сначала нужно переместить её, а затем повернуть. Благодаря этому изменённому порядку ко времени поворота центр фигуры станет центром системы координат.
float scene(float2 position) {
float2 circlePosition = position;
circlePosition = translate(circlePosition, float2(2, 0));
circlePosition = rotate(circlePosition, _Time.y);
float sceneDistance = rectangle(circlePosition, float2(1, 2));
return sceneDistance;
}
Масштабирование
Масштабирование работает аналогично другим способам преобразования фигур. Мы делим координаты на масштаб, отрисовывая фигуру в пространстве с уменьшенным масштабом, и в базовой системе координат они становятся больше.
float2 scale(float2 samplePosition, float scale){
return samplePosition / scale;
}float scene(float2 position) {
float2 circlePosition = position;
circlePosition = translate(circlePosition, float2(0, 0));
circlePosition = rotate(circlePosition, .125);
float pulseScale = 1 + 0.5*sin(_Time.y * 3.14);
circlePosition = scale(circlePosition, pulseScale);
float sceneDistance = rectangle(circlePosition, float2(1, 2));
return sceneDistance;
}
Хотя это выполняет масштабирование правильно, расстояние тоже масштабируется. Основное преимущество поля расстояний со знаком заключается в том, что мы всегда знаем расстояние до ближайшей поверхности, но изменение масштаба полностью уничтожает данное свойство. Это можно легко исправить, умножив поле расстояний, полученное от функции расстояния со знаком (в нашем случае
rectangle), на масштаб. По той же причине мы не можем легко масштабировать неравномерно (с разными масштабами для осей x и y).float scene(float2 position) {
float2 circlePosition = position;
circlePosition = translate(circlePosition, float2(0, 0));
circlePosition = rotate(circlePosition, .125);
float pulseScale = 1 + 0.5*sin(_Time.y * 3.14);
circlePosition = scale(circlePosition, pulseScale);
float sceneDistance = rectangle(circlePosition, float2(1, 2)) * pulseScale;
return sceneDistance;
}
Визуализация
Поля расстояний со знаком можно использовать для разных вещей, например, создания теней, рендеринга 3D-сцен, физики и рендеринга текста. Но мы пока не хотим углубляться в сложности, поэтому я объясню только две техники их визуализации. Первая — чёткая форма со сглаживанием (antialiasing), вторая — рендеринг линий в зависимости от расстояния.
Чёткая форма
Этот метод схож с тем, который часто используется при рендеринге текста, он создаёт чёткую форму. Если мы хотим генерировать поле расстояний не из функции, а будем считывать её из текстуры, то это позволяет нам использовать текстуры с гораздо меньшим разрешением, чем обычно, и получать хорошие результаты. TextMesh Pro использует эту технику для рендеринга текста.
Для применения этой техники мы пользуемся тем фактом, что данные в полях расстояний со знаком, и нам известна точка отсечки. Мы начинаем с вычисления того, насколько поле расстояний изменяется к следующему пикселю. Это должна быть та же величина, что и длина изменения координат, но проще и надёжнее вычислять расстояние со знаком.
Получив изменение расстояния, мы можем сделать smoothstep с половины изменения расстояния до минус/плюс половины изменения расстояния. Это выполнит простую отсечку примерно около 0, но со сглаживанием. Затем можно использовать это сглаженное значение для любого нужного нам двоичного значения. В этом примере я сменю шейдер на шейдер прозрачности и использую его для альфа-канала. Я делаю smoothstep с положительного на отрицательное значение потому, что мы хотим, чтобы было видимым отрицательное значение поля расстояний. Если вы не совсем понимаете, как здесь работает рендеринг прозрачности, то рекомендую прочитать мой туториал по рендерингу прозрачности.
//properties
Properties{
_Color("Color", Color) = (1,1,1,1)
}//in subshader outside of pass
Tags{ "RenderType"="Transparent" "Queue"="Transparent"}
Blend SrcAlpha OneMinusSrcAlpha
ZWrite Offfixed4 frag(v2f i) : SV_TARGET{
float dist = scene(i.worldPos.xz);
float distanceChange = fwidth(dist) * 0.5;
float antialiasedCutoff = smoothstep(distanceChange, -distanceChange, dist);
fixed4 col = fixed4(_Color, antialiasedCutoff);
return col;
}
Линии высот
Ещё одна распространённая техника визуализации полей расстояний заключается в отображении расстояний в виде линий. В нашей реализации я добавлю несколько толстых линий и несколько тонких между ними. Также я раскрашу внутреннюю и наружную части фигуры в разные цвета, чтобы было видно, где находится объект.
Мы начнём с отображения разницы между внутренней и внешней частями фигуры. Цвета можно будет настраивать в материале, поэтому мы добавим новые свойства, а также переменные шейдера для внутреннего и внешнего цветов фигуры.
Properties{
_InsideColor("Inside Color", Color) = (.5, 0, 0, 1)
_OutsideColor("Outside Color", Color) = (0, .5, 0, 1)
}//global shader variables
float4 _InsideColor;
float4 _OutsideColor;Затем во фрагментном шейдере мы проверяем, где находится пиксель, который мы рендерим, сравнивая расстояние со знаком с 0 при помощи функции
step. Мы используем эту переменную для интерполяции от внутреннего до внешнего цвета и рендеринга его на экране.fixed4 frag(v2f i) : SV_TARGET{
float dist = scene(i.worldPos.xz);
fixed4 col = lerp(_InsideColor, _OutsideColor, step(0, dist));
return col;
}
Чтобы отрендерить линии, нам сначала нужно указать, как часто мы будем рендерить линии, и насколько толстыми они будут, задав свойства и соответствующие переменные шейдера.
//Properties
_LineDistance("Mayor Line Distance", Range(0, 2)) = 1
_LineThickness("Mayor Line Thickness", Range(0, 0.1)) = 0.05//shader variables
float _LineDistance;
float _LineThickness;Затем для рендеринга линий мы начнём с вычисления изменения расстояния, чтобы в дальнейшем использовать его для сглаживания. Также мы уже поделили его на 2, потому что позже мы прибавим его половину и вычтем его половину, чтобы покрыть расстояние изменения в 1 пиксель.
float distanceChange = fwidth(dist) * 0.5;Затем мы берём расстояние и преобразовываем его таким образом, чтобы оно имело одинаковое поведение в повторяющихся точках. Для этого мы сначала разделим его на расстояние между линиями, при этом у нас не получатся полные числа на каждом первом шаге, а полные числа только на основании заданного нами расстояния.
Затем мы прибавляем к числу 0.5, берём дробную часть и снова вычитаем 0.5. Дробная часть и вычитание нужны здесь для того, чтобы линия проходила через ноль в повторяющемся паттерне. Прибавляем мы 0.5 до получения дробной части для того, чтобы нейтрализовать дальнейшее вычитание 0.5 — смещение приведёт к тому, что значения, при которых график равен 0, находятся в 0, 1, 2 и т.д., а не в 0.5, 1.5, и т.д.
Последние шаги для преобразования значения — мы берём абсолютное значение и снова умножаем его на расстояние между линиями. Абсолютное значение делает так, что области до и после точек линии остаются такими же, что упрощает создание отсечки для линий. Последняя операция, в которой мы снова умножаем значение на расстояние между линиями, нужна, чтобы нейтрализовать деление в начале уравнения, благодаря нему изменение в значении снова такое же, как в начале, а вычисленное нами ранее изменение расстояния по-прежнему является верным.

float majorLineDistance = abs(frac(dist / _LineDistance + 0.5) - 0.5) * _LineDistance;Теперь, когда мы вычислили расстояние до линий на основании расстояния до фигуры, можно отрисовать линии. Мы выполняем smoothstep от linethickness минус половина изменения расстояния до linethickness плюс половина изменения расстояния и используем только что вычисленное расстояние линии в качестве значения для сравнения. После вычисления этого значения мы умножаем его на цвет, чтобы создать чёрные линии (можно также выполнить lerp до другого цвета, если вам нужны разноцветные линии).
fixed4 frag(v2f i) : SV_TARGET{
float dist = scene(i.worldPos.xz);
fixed4 col = lerp(_InsideColor, _OutsideColor, step(0, dist));
float distanceChange = fwidth(dist) * 0.5;
float majorLineDistance = abs(frac(dist / _LineDistance + 0.5) - 0.5) * _LineDistance;
float majorLines = smoothstep(_LineThickness - distanceChange, _LineThickness + distanceChange, majorLineDistance);
return col * majorLines;
}
Тонкие линии между толстыми мы реализуем аналогичным образом — добавляем свойство, определяющее, сколько тонких линий должно быть между толстыми, а потом делаем то же, что делали с толстыми, но из-за расстояния между тонкими линиями делим расстояние между толстыми на количество тонких линий между ними. Также мы сделаем количество тонких линий
IntRange, благодаря этому мы сможем назначать только целые значения и не получим тонкие линии, несоответствующие толстым. После вычисления тонких линий мы умножаем их на цвет точно так же, как и толстые.//properties
[IntRange]_SubLines("Lines between major lines", Range(1, 10)) = 4
_SubLineThickness("Thickness of inbetween lines", Range(0, 0.05)) = 0.01//shader variables
float _SubLines;
float _SubLineThickness;fixed4 frag(v2f i) : SV_TARGET{
float dist = scene(i.worldPos.xz);
fixed4 col = lerp(_InsideColor, _OutsideColor, step(0, dist));
float distanceChange = fwidth(dist) * 0.5;
float majorLineDistance = abs(frac(dist / _LineDistance + 0.5) - 0.5) * _LineDistance;
float majorLines = smoothstep(_LineThickness - distanceChange, _LineThickness + distanceChange, majorLineDistance);
float distanceBetweenSubLines = _LineDistance / _SubLines;
float subLineDistance = abs(frac(dist / distanceBetweenSubLines + 0.5) - 0.5) * distanceBetweenSubLines;
float subLines = smoothstep(_SubLineThickness - distanceChange, _SubLineThickness + distanceChange, subLineDistance);
return col * majorLines * subLines;
}
Исходный код
Двухмерные функции SDF
#ifndef SDF_2D
#define SDF_2D
float2 rotate(float2 samplePosition, float rotation){
const float PI = 3.14159;
float angle = rotation * PI * 2 * -1;
float sine, cosine;
sincos(angle, sine, cosine);
return float2(cosine * samplePosition.x + sine * samplePosition.y, cosine * samplePosition.y - sine * samplePosition.x);
}
float2 translate(float2 samplePosition, float2 offset){
//move samplepoint in the opposite direction that we want to move shapes in
return samplePosition - offset;
}
float2 scale(float2 samplePosition, float scale){
return samplePosition / scale;
}
float circle(float2 samplePosition, float radius){
//get distance from center and grow it according to radius
return length(samplePosition) - radius;
}
float rectangle(float2 samplePosition, float2 halfSize){
float2 componentWiseEdgeDistance = abs(samplePosition) - halfSize;
float outsideDistance = length(max(componentWiseEdgeDistance, 0));
float insideDistance = min(max(componentWiseEdgeDistance.x, componentWiseEdgeDistance.y), 0);
return outsideDistance + insideDistance;
}
#endifПример с кругом
Shader "Tutorial/034_2D_SDF_Basics/Rectangle"{
SubShader{
//the material is completely non-transparent and is rendered at the same time as the other opaque geometry
Tags{ "RenderType"="Opaque" "Queue"="Geometry"}
Pass{
CGPROGRAM
#include "UnityCG.cginc"
#include "2D_SDF.cginc"
#pragma vertex vert
#pragma fragment frag
struct appdata{
float4 vertex : POSITION;
};
struct v2f{
float4 position : SV_POSITION;
float4 worldPos : TEXCOORD0;
};
v2f vert(appdata v){
v2f o;
//calculate the position in clip space to render the object
o.position = UnityObjectToClipPos(v.vertex);
//calculate world position of vertex
o.worldPos = mul(unity_ObjectToWorld, v.vertex);
return o;
}
float scene(float2 position) {
float2 circlePosition = position;
circlePosition = rotate(circlePosition, _Time.y * 0.5);
circlePosition = translate(circlePosition, float2(2, 0));
float sceneDistance = rectangle(circlePosition, float2(1, 2));
return sceneDistance;
}
fixed4 frag(v2f i) : SV_TARGET{
float dist = scene(i.worldPos.xz);
fixed4 col = fixed4(dist, dist, dist, 1);
return col;
}
ENDCG
}
}
FallBack "Standard" //fallback adds a shadow pass so we get shadows on other objects
}Пример с прямоугольником
Shader "Tutorial/034_2D_SDF_Basics/Rectangle"{
SubShader{
//the material is completely non-transparent and is rendered at the same time as the other opaque geometry
Tags{ "RenderType"="Opaque" "Queue"="Geometry"}
Pass{
CGPROGRAM
#include "UnityCG.cginc"
#include "2D_SDF.cginc"
#pragma vertex vert
#pragma fragment frag
struct appdata{
float4 vertex : POSITION;
};
struct v2f{
float4 position : SV_POSITION;
float4 worldPos : TEXCOORD0;
};
v2f vert(appdata v){
v2f o;
//calculate the position in clip space to render the object
o.position = UnityObjectToClipPos(v.vertex);
//calculate world position of vertex
o.worldPos = mul(unity_ObjectToWorld, v.vertex);
return o;
}
float scene(float2 position) {
float2 circlePosition = position;
circlePosition = rotate(circlePosition, _Time.y * 0.5);
circlePosition = translate(circlePosition, float2(2, 0));
float sceneDistance = rectangle(circlePosition, float2(1, 2));
return sceneDistance;
}
fixed4 frag(v2f i) : SV_TARGET{
float dist = scene(i.worldPos.xz);
fixed4 col = fixed4(dist, dist, dist, 1);
return col;
}
ENDCG
}
}
FallBack "Standard" //fallback adds a shadow pass so we get shadows on other objects
}Отсечка
Shader "Tutorial/034_2D_SDF_Basics/Cutoff"{
Properties{
_Color("Color", Color) = (1,1,1,1)
}
SubShader{
Tags{ "RenderType"="Transparent" "Queue"="Transparent"}
Blend SrcAlpha OneMinusSrcAlpha
ZWrite Off
Pass{
CGPROGRAM
#include "UnityCG.cginc"
#include "2D_SDF.cginc"
#pragma vertex vert
#pragma fragment frag
struct appdata{
float4 vertex : POSITION;
};
struct v2f{
float4 position : SV_POSITION;
float4 worldPos : TEXCOORD0;
};
fixed3 _Color;
v2f vert(appdata v){
v2f o;
//calculate the position in clip space to render the object
o.position = UnityObjectToClipPos(v.vertex);
//calculate world position of vertex
o.worldPos = mul(unity_ObjectToWorld, v.vertex);
return o;
}
float scene(float2 position) {
float2 circlePosition = position;
circlePosition = rotate(circlePosition, _Time.y * 0.5);
circlePosition = translate(circlePosition, float2(2, 0));
float sceneDistance = rectangle(circlePosition, float2(1, 2));
return sceneDistance;
}
fixed4 frag(v2f i) : SV_TARGET{
float dist = scene(i.worldPos.xz);
float distanceChange = fwidth(dist) * 0.5;
float antialiasedCutoff = smoothstep(distanceChange, -distanceChange, dist);
fixed4 col = fixed4(_Color, antialiasedCutoff);
return col;
}
ENDCG
}
}
FallBack "Standard" //fallback adds a shadow pass so we get shadows on other objects
}Линии расстояний
Shader "Tutorial/034_2D_SDF_Basics/DistanceLines"{
Properties{
_InsideColor("Inside Color", Color) = (.5, 0, 0, 1)
_OutsideColor("Outside Color", Color) = (0, .5, 0, 1)
_LineDistance("Mayor Line Distance", Range(0, 2)) = 1
_LineThickness("Mayor Line Thickness", Range(0, 0.1)) = 0.05
[IntRange]_SubLines("Lines between major lines", Range(1, 10)) = 4
_SubLineThickness("Thickness of inbetween lines", Range(0, 0.05)) = 0.01
}
SubShader{
//the material is completely non-transparent and is rendered at the same time as the other opaque geometry
Tags{ "RenderType"="Opaque" "Queue"="Geometry"}
Pass{
CGPROGRAM
#include "UnityCG.cginc"
#include "2D_SDF.cginc"
#pragma vertex vert
#pragma fragment frag
struct appdata{
float4 vertex : POSITION;
};
struct v2f{
float4 position : SV_POSITION;
float4 worldPos : TEXCOORD0;
};
v2f vert(appdata v){
v2f o;
//calculate the position in clip space to render the object
o.position = UnityObjectToClipPos(v.vertex);
//calculate world position of vertex
o.worldPos = mul(unity_ObjectToWorld, v.vertex);
return o;
}
float scene(float2 position) {
float2 circlePosition = position;
circlePosition = rotate(circlePosition, _Time.y * 0.2);
circlePosition = translate(circlePosition, float2(2, 0));
float sceneDistance = rectangle(circlePosition, float2(1, 2));
return sceneDistance;
}
float4 _InsideColor;
float4 _OutsideColor;
float _LineDistance;
float _LineThickness;
float _SubLines;
float _SubLineThickness;
fixed4 frag(v2f i) : SV_TARGET{
float dist = scene(i.worldPos.xz);
fixed4 col = lerp(_InsideColor, _OutsideColor, step(0, dist));
float distanceChange = fwidth(dist) * 0.5;
float majorLineDistance = abs(frac(dist / _LineDistance + 0.5) - 0.5) * _LineDistance;
float majorLines = smoothstep(_LineThickness - distanceChange, _LineThickness + distanceChange, majorLineDistance);
float distanceBetweenSubLines = _LineDistance / _SubLines;
float subLineDistance = abs(frac(dist / distanceBetweenSubLines + 0.5) - 0.5) * distanceBetweenSubLines;
float subLines = smoothstep(_SubLineThickness - distanceChange, _SubLineThickness + distanceChange, subLineDistance);
return col * majorLines * subLines;
}
ENDCG
}
}
FallBack "Standard" //fallback adds a shadow pass so we get shadows on other objects
}Надеюсь, мне удалось объяснить основы полей расстояний со знаком, и вы уже ждёте несколько новых туториалов, в которых я расскажу о других способах их применения.


FadeToBlack
Очень плохой перевод. Я знаю об SDF многое, работал с ними, но даже мне сложно понять, о чем идет речь. Простите, но такой перевод никуда не годится (