Когда я пришёл домой, я задумался над этим вопросом. Поискал решение этой задачи на форумах. Кто-то был согласен со мной, но многие учли, что операция смещения производится native методом, который работает быстрее, поэтому ArrayList выполнит вставку в середину быстрее. Не получив окончательного и неопровержимого ответа, я решил провести собственное исследование.
Сперва я углубился в изучение исходного кода этих классов. Вставка элемента в ArrayList проходит так: сначала, при необходимости, массив увеличивается, затем все элементы, стоящие после места вставки сдвигаются на число позиций, равное количеству вставляемых элементов (я рассматриваю один элемент), и в конце встаёт на свое место вставляемый элемент. Массив увеличивается со скоростью n*1,5, где n — размер массива, а минимальное увеличение при стандартных условиях (capacity=10) — 5 элементов. В связи с этим, операцией по увеличению массива при расчёте алгоритмической сложности вставки можно пренебречь. Сдвиг элементов, находящихся после точки вставки обладает алгоритмической сложностью O(n). Таким образом общая сложность всё равно остаётся O(n). Да, мы держим в уме, что операция увеличения массива незначительно повышает сложность, но нативность действий с массивом увеличивает скорость работы.
Поиск элемента в LinkedList начинается в цикле от края списка. Если искомый элемент находится в первой половине списка, то поиск идёт с начала, в обратном случае — с конца. Так как мы вставляем именно в середину, то в цикле пройдём ровно половину элементов. Сложность O(n). Сама вставка, как я уже писал выше, заключается в создании объекта и указании ссылок на него. Сложность O(1). Опять же ничего нового я не выяснил: общая сложность осталась O(n), при этом держим в уме, что создание объекта — «дорогая» операция.
Анализ исходного кода ситуацию не разъяснил, поэтому стал писать тесты. Я решил исследовать зависимость от двух параметров: начальный размер списка и количество вставок подряд (количество итераций).
package com.jonasasx.liststest;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
public class Main {
private static final int MAX_SIZE = 1000;
private static final int MAX_ITERATIONS = 10000;
private static final float STEP_SIZE = 2f;
private static final float STEP_ITERATIONS = 5;
private static final int TESTS_COUNT = 100;
public static void main(String[] args) throws InterruptedException {
ArrayList<String> arrayList;
LinkedList<String> linkedList;
for (float size = 1; size < MAX_SIZE; size *= STEP_SIZE) {
for (float iterations = 1; iterations < MAX_ITERATIONS; iterations *= STEP_ITERATIONS) {
double sum = 0;
for (int k = 0; k < TESTS_COUNT; k++) {
arrayList = new ArrayList<>();
linkedList = new LinkedList<>();
fillList(arrayList, (int) size);
fillList(linkedList, (int) size);
sum += Math.log10(calculateRatio(arrayList, linkedList, (int) iterations));
}
double logRatio = sum / TESTS_COUNT;
System.out.println(String.format("%07d\t%07d\t%07.2f\t%s", (int) size, (int) iterations, logRatio, logRatio > 0 ? "Linked" : "Array"));
}
System.out.println();
}
}
static void fillList(List<String> list, int size) {
for (int i = 0; i < size; i++) {
list.add("0");
}
}
static double calculateRatio(ArrayList<String> arrayList, LinkedList<String> linkedList, int iterations) {
long l1 = calculateAL(arrayList, iterations);
long l2 = calculateLL(linkedList, iterations);
if (l1 == 0 || l2 == 0)
throw new java.lang.IllegalStateException();
return (double) l1 / (double) l2;
}
static long calculateAL(ArrayList<String> list, int m) {
long t = System.nanoTime();
for (int i = 0; i < m; i++) {
list.add(list.size() / 2, "0");
}
return System.nanoTime() - t;
}
static long calculateLL(LinkedList<String> list, int m) {
long t = System.nanoTime();
for (int i = 0; i < m; i++) {
list.add(list.size() / 2, "0");
}
return System.nanoTime() - t;
}
}
Для каждого размера списка и количества итераций создаются по одному массиву ArrayList и LinkedList, они заполняются одинаковыми объектами, после чего под замер скорости производится n вставок одного объекта в середину. В качестве сравниваемой величины я использую десятичный логарифм от отношения времён выполнения ArrayList к LinkedList. Когда это значение меньше нуля, ArrayList справляется быстрее, когда больше — быстрее LinkedList.
Привожу результаты теста в таблице:
| Итераций | |||||||||||
| Размер | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | |
| 1 | -0,12 | 0,01 | -0,04 | 0,01 | 0,03 | -0,04 | -0,09 | -0,19 | -0,21 | -0,31 | |
| 5 | -0,14 | 0,02 | -0,02 | 0,07 | -0,08 | 0 | -0,15 | -0,31 | -0,42 | -0,52 | |
| 25 | -0,12 | 0,2 | 0,19 | 0,13 | 0,07 | 0,04 | -0,1 | -0,29 | -0,47 | -0,56 | |
| 125 | -0,31 | -0,01 | 0,01 | 0 | -0,03 | -0,11 | -0,17 | -0,35 | -0,48 | -0,57 | |
| 625 | -0,47 | -0,49 | -0,48 | -0,45 | -0,49 | -0,51 | -0,53 | -0,6 | -0,67 | -0,78 |
И в графике:

На оси X указан изначальный размер списка, линии представляют разные количества итераций, а на оси Y отношение скорости работы двух реализаций списка.
Так как с каждой итерацией размер списка увеличивается, можно сделать общий вывод: LinkList работает быстрее при небольшом размере списка. Но самое главное: без чёткой конкретизации условий сравнивать скорость работы этих двух алгоритмов нельзя!
Чтобы увеличить точность, я отказался от параметра количества вставок и уменьшил шаг размера до одного. Для каждого из размеров я провёл тест тысячу раз и взял среднее значение. Получил график:
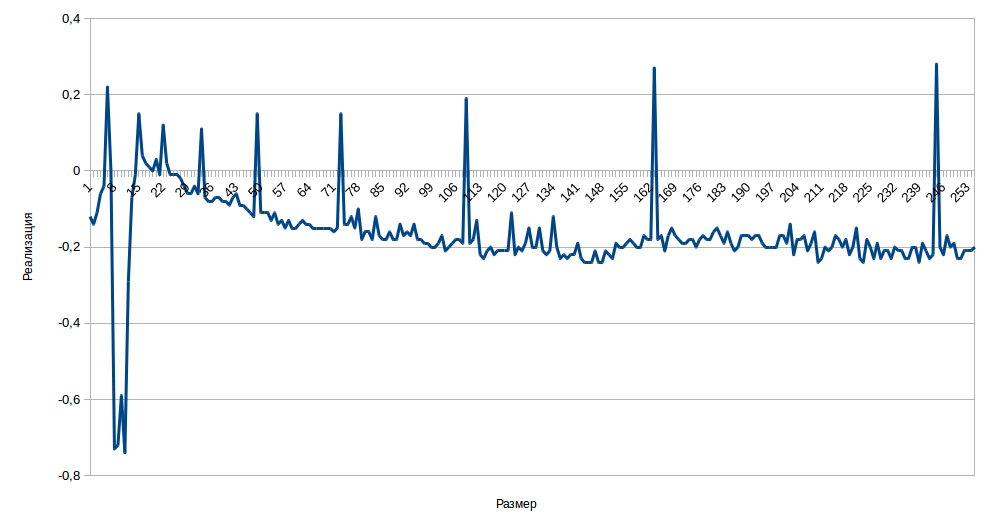
На графике ярко выражены всплески. Они находятся точно на тех местах, где ArrayList производит увеличение массива. Следовательно, можно сказать, что пренебрегать этой операцией нельзя, как я посчитал в начале, анализируя исходный код.
Общий вывод можно сделать такой: операция вставки в середину происходит в основном быстрее в ArrayList, но не всегда. С теоретической точки зрения нельзя однозначно сравнить скорость этих двух алгоритмов без учёта изначального размера списка.
Спасибо за внимание, надеюсь, кому-то моя работа покажется интересной и/или полезной.
Комментарии (115)

roman_kashitsyn
18.07.2015 09:10+5Извините, конечно, но никакого практического интереса в вашем исследовании нет.
Если нужно часто вставлять в середину списка, то структура данных выбрана неправильно, просто не используйте список. Если список маленький, а операция редкая, то принципиальной разницы нет.
jonasas Автор
18.07.2015 12:04+7Да, согласен, практического интереса нет. Мне было интересно ответить на конкретно поставленный теоретический вопрос.

zw0rk
18.07.2015 15:42-1По-моему, на теоретическую часть вопроса вы ответили на собеседовании. А всё остальное это эксперименты над конкретной реализацией.

khim
19.07.2015 00:08-2Ну как вас сказать, чтобы не обидеть… тот факт, что на собеседовании был дан неправильный, по сути, ответ, вас не удивляет, нет?
Забавно что очень похожую задачу мы «мимолётом» обсуждали чисто теоретически вот тут. Там, правда, речь шла о C++, а это меняет дело (Java добавляет в задачу изрядно «левых» накладных расходов, так что преимущество массива начинает проявляться не сразу, а с какого-то момента) и про удаление элементов, а не про их добавление (а это сильно меняет дело), но всё-таки идея похожая.
zw0rk
19.07.2015 06:03> Ну как вас сказать, чтобы не обидеть… тот факт, что на собеседовании был дан неправильный, по сути, ответ, вас не удивляет, нет?
Я в своём комментарии где-то рассуждал о правильности ответа на теоретическую часть вопроса?
chabapok
18.07.2015 10:21-9Есть следующий вопрос. Правильно ли я понимаю следующее. Сложности, которыми вы оперируете, находятся в разных координатных системах. Т.е., если у ArrayList и LinkedList параметр O(1) равен разному физическому времени, поэтому одинаковые сложности O(n) — не означают, что время вставки будет одинаково. Оно может ощутимо различаться.
А если мы пробегаем не весь linkedList, а как максимум его половину — сложность точно будет O(n)? Может, O(n/2) или O(n)/2? Мы же пробегаем половину.
Вообще, вопрос был с подвохом. ИМХО, если он звучал именно так, как вы написали — вы вообще не по той ветке пошли. Надо было сказать, что вставка по индексу и вставка по итератору отличаются. Поэтому, для практического применения имеет смысл сравнивать не одинаковые подходы в использовании этих сущностей, а разные. Потому, что если будешь писать программу и встанет вопрос ArrayList или LinedList — то очевидно, что для LinedList будет предполагаться использование итераторов. А если использование итераторов невозможно изза специфики алгоритма — то и вопрос такой (у правильного программиста) не возникнет. Поэтому с практической точки зрения, логичней было бы сравнивать скорость вставки в ArrayList по индексу со скоростью вставки в LinkedList по итератору. Плюс рассказать про накладные расходы, в том плане что создаются LinkedList.Nodegurinderu
18.07.2015 11:57+1O(n) приблизительная оценка и показывает скорость роста функции. Она не может быть O(n/2)

simbajoe
19.07.2015 00:17+2Почему же не может? Может. Но O(n) = O(n/2), поэтому разницы никакой нет.
gurinderu
19.07.2015 12:03+1Абсолютно верно. Они равны и не смысл писать или говорить о дроби. Если я услышу такой ответ на собеседовании, то с вероятностью 90 процентов человек не понимает, что такое трудоемкость)

Rupper
19.07.2015 18:59Совсем точно стоило бы говорить о ассимптотическом количестве операций для машины Тюринга.
О(F) и о(F) проходят в первом семестре матанализа.
Однако, на машине Тьюринга адресования нет, а чтение «заданной» ячейки выполняется путем последовательного перемещения.
Если два алгоритма ассимптотически эквивалентны по сложности, то отличаются они только компоненты низших порядков. Т.е. для двух алгоритмов O(n) — в константу раз.

jonasas Автор
18.07.2015 12:09+1Есть следующий вопрос. Правильно ли я понимаю следующее. Сложности, которыми вы оперируете, находятся в разных координатных системах. Т.е., если у ArrayList и LinkedList параметр O(1) равен разному физическому времени, поэтому одинаковые сложности O(n) — не означают, что время вставки будет одинаково. Оно может ощутимо различаться.
Да, скорость выполнение операций — разная, а сложность — одна. Это можно сравнить с испытанием одного алгоритма на машинах разной производительности.
А если мы пробегаем не весь linkedList, а как максимум его половину — сложность точно будет O(n)? Может, O(n/2) или O(n)/2? Мы же пробегаем половину.
Кстати, в ArrayList мы тоже смещаем только половину массива.
Вообще, вопрос был с подвохом. ИМХО, если он звучал именно так, как вы написали — вы вообще не по той ветке пошли. Надо было сказать, что вставка по индексу и вставка по итератору отличаются.
Да, тут согласен, про вставку по итератору я тогда не догадался сказать.chabapok
18.07.2015 13:56насчет «Кстати, в ArrayList мы тоже смещаем только половину массива.»
С ArrayList весь массив будет смещаться, если вставляем по индексу 0. С LinkedList мы пробегаем не более половины массива.
jonasas Автор
18.07.2015 14:08Согласен. Но я опять же мыслю в контексте текущей проблемы, где вставка идёт именно в середину списка. И, кстати, усреднённая точка вставки для общего случая будет с=(1+2+...+n)/n=n/2, опять же середина списка.

hmspns
18.07.2015 11:35+1Не уверен на 100% на счёт Java, но предполагаю, что при увеличении массива, будет просто выделен новый кусок памяти, большего размера, куда будут скопированы значения из старого размера. При этом старый кусок памяти придётся удалять, т.е. дополнительно вырастет нагрузка на сборщик мусора.

jonasas Автор
18.07.2015 12:12Да, эту проблему я тоже учитывал в тесте, вызывая сборщик мусора и паузу для его работы после каждой новой инициализации списков, но какого-то видимого изменения статистики я не увидел.

vedenin1980
18.07.2015 20:17Да, именно поэтому всегда рекомендуют задавать у ArrayList capacity заранее используя оценку сверху, но вот с Linked List все ещё хуже — каждый элемент это объект Node, соответственно создав Linked List на 100 тыс. элементов и потом удалив на него ссылку, ты заставляешь сборщик мусора мучительно вычищать 100 тыс.объектов. Нет, конечно, очистка памяти копированием у первого поколения вещь отличная, но все-таки…

lany
20.07.2015 09:42+3Просто нужно время, чтобы люди поняли простую истину: LinkedList — практически бесполезная структура данных. Количество ситуаций, где её использование оправдано, стремится к нулю.

hmspns
20.07.2015 09:48-1Предполагаю, её использование оправдано в ситуациях, когда надо часто удалять элементы из середины списка. Поскольку в ArrayList при этом происходит сдвиг элементов, каждое такое удаление будет сопровождаться выделением памяти под новый массив и копирование в него оставшихся элементов из старого. В LinkedList просто меняются указатели у соседей удаляемого элемента.

vedenin1980
20.07.2015 10:39+2Поскольку в ArrayList при этом происходит сдвиг элементов, каждое такое удаление будет сопровождаться выделением памяти под новый массив и копирование в него оставшихся элементов из старого.
Нет, специально посмотрел исходный код, при удалении происходит копирование памяти в одном массиве, т.е. просто все элементы сдвигаются на один вперед.
Предполагаю, её использование оправдано в ситуациях, когда надо часто удалять элементы из середины списка.
Проблема в том что надо ещё двигаться по этому списку (слабо представляю кейс при котором требовалось бы стоять на одном месте и по одному удалять элементы), а это не быстро. Если действительно возникает ситуация удаления элементов, я бы использовал ArrayList (или вообще простой массив, если начальный размер точно известен) и записывал вместо удаления null, а в конце просто убрал бы все null элементы или при итерировании игнорировал бы null значения. Учитывая как дорого итерироваться по результирующему LinkedList, проверка на null при итерировании по ArrayList/массиву будет все равно быстрее.

lany
20.07.2015 14:40+1Когда надо удалять из середины, чаще оказывается, что логичнее использовать LinkedHashSet или LinkedHashMap.
gurinderu
20.07.2015 10:23*trolling* А если нужно иметь список больше Integer.MAX_VALUE?)

vedenin1980
20.07.2015 10:43Тогда у вас неверная архитектура, даже ArrayList такого размера это 17 Гб, LinkedList — боюсь даже думать сколько. :)

lany
20.07.2015 14:43+1Почему 17? С CompressedOops в районе 8. А насчёт LinkedList как раз недавно спрашивали.
gurinderu
20.07.2015 17:48Да тут вообще интересна методика подсчета) 17 для чего? Какой содержимое листа Integer,String, Long или может что-то свое? Или считались только заголовки?

lany
20.07.2015 19:27+1Разумеется, считать надо только расходы памяти на саму структуру данных, а не на объекты, что в ней размещены.

vedenin1980
20.07.2015 21:41Какой содержимое листа Integer,String, Long или может что-то свое? Или считались только заголовки?
Понимаете «содержимое листа» не важно, дело в том что все стандартные Java коллекции не хранят ничего кроме ссылок на объекты, причем в тот же List можно вставить один единственный объект миллион раз (на самом деле, конечно, в листе будет миллион одинаковых ссылок на этот объект). Естественно, имеет смысл говорить только о размере коллекции, а не о размерах объектов на которые она указывает (тем более что там могут быть одни null'ы, например).gurinderu
20.07.2015 23:01Согласен, но не понятно утверждение про 17Гб т.к ссылки бывают разные) И даже в x64 вы промазали на 1Гб )

khim
20.07.2015 23:18-1Хм… В x64 режиме без всяких компрессий 2147483647 ссылок займут 17179869176 байт, что есть примерно 17Гб… или вы считаете ошибку в 1.05% слишком большой и считате, что нужно обязательно писать про 17.2Гб???
gurinderu
21.07.2015 08:11-1не забывайте что 1килобайт = 1024 байта?

Mrrl
21.07.2015 08:36-21024 байта — это кибибайт. А килобайт — только 1000 байт.
gurinderu
21.07.2015 10:00Более поздний документ, «Положение о единицах величин, допускаемых к применению в Российской Федерации», утверждённое Правительством РФ 31 октября 2009 года, устанавливает, что наименование и обозначение единицы количества информации «байт» (1 байт = 8 бит) применяются с двоичными приставками «Кило», «Мега», «Гига», которые соответствуют множителям 2^10, 2^20 и 2^30 (1 Кбайт = 1024 байт, 1 Мбайт = 1024 Кбайт, 1 Гбайт = 1024 Мбайт)

khim
21.07.2015 13:10Именно поэтому я и не использую названия Кбайт, Мбайт и Гбайт, так как они только всех запутывают. Есть Кб = 1000 байт, есть КиБ = 1024 байта, а юридические названия, возникшие в чьём-то воспалённом мозгу оставьте юристам. Заметьте, что само по себе это постановление говорит «В Российской Федерации допускаются к применению основные единицы СИ, производные единицы СИ и отдельные внесистемные единицы величин», однако потом описывает-таки все эти единицы отдельно. И что применять когда международные организации говорят одно/a>, а постановление — другое?
P.S. Контрольный вопрос: сколько байт влазит на 1.44MB дискету? Меня ответ на этот вопрос когда-то убедил отказаться-таки от попыток «угадывать» по контексту вид приставки. А «постановление правительства»… ну что ж теперь с ним делать… не использовать со словом «байт» приставок «К», «М» и «Г», пока его не поправят, вот и всё. Про Кб или Тб постановление ничего не говорит, а про международные приставки говорит, но у них свои хозяева есть. Просто стандарт ISO 80000-1:2009, в котором, наконец-то, навели порядок со всеми этими приставками вышел (как несложно догадаться из названия) в том же 2009м году, что и постановление правительства, а ГОСТ 8.417-2002 (на котором это постановление основано) вышел гораздо раньше и с тех пор никто не озаботился внести поправки. Бывает.

Maccimo
23.07.2015 18:44+2За использование всяких «кирбибайтов» нужно линейкой по пальцам бить.
Килобайт это 1024 байта и точка.

vedenin1980
21.07.2015 06:56Вообще, сейчас основные архитектуры x32 и x64, в x32 такой размер памяти физически не выделить без всяких шаманских методом, соответственно он в этом случае не подойдет.

khim
21.07.2015 13:23+2Не поминайте x32 всуе, я вас очень прошу. Это — весьма экзотическая, мало кем используемая, вещь, не надо ещё и её сюда за уши притягивать. Есть x86 и x86-64, можно ещё названия IA32 и x64 встретить, а вот x32 — не стоит, это другое.
P.S. И не забудьте, что IA64 в природе тоже есть и это совсем не то же самое, что x86-64 aka x64.
P.P.S. Да, мне тоже хочется иметь какие-то «симметричные» названия, чтобы можно было цифирьку 32 на 64 поменять и всё — переход от 32бит к 64битам совершён. Но, увы, не судьба: все осмысленные названия заняты. Кроме, пожалуй, Intel 32 и Intel 64, но эти названия ещё кое-как узнаются на английском, а на русском их даже Wikipedia не признаёт!

matiouchkine
20.07.2015 11:53Дональд Кнут и его «пляшущие ссылки» в недоумении. stackoverflow.com/questions/11700147/the-data-structure-of-knuths-dancing-links-algorithm
encyclopedist
22.07.2015 16:20+3На практических задачах Dancing Links обычно работает медленнее, чем битовые карты.
Это один из примеров «устаревших оптимизаций». У современных компьютеров совсем другие соотношения стоимости операций, чем у компьютеров времен Кнута.

shapovalex
18.07.2015 11:59+6Думаю большую роль здесь начинает играть такая тонкая материя, как кэш процессора. При пробеге по LinkedList количество кэш-промахов велико и итерирование происходит медленно. При сдвиге же количество промахов снижается, поэтому операция сдвига и происходит быстро.

jonasas Автор
18.07.2015 12:18Поясните, пожалуйста, почему при сдвиге кэш используется больше? За счёт того, что мы двигаемся линейно по памяти, а не прыгаем ко куче?

a553
18.07.2015 12:40+2Именно. Условно говоря, прочитав первый байт массива из памяти процессор положит следующие N байтов в кеш, и их чтение будет происходить на несколько порядков быстрее.

khim
19.07.2015 00:17Угу. Ключевые слова для Гугла — «предвыборка данных» (data prefetch).

leventov
19.07.2015 01:09+1Роль предвыборки небольшая, когда на одной кеш-линии помещаются 8(16) элементов массива. Т. е. основной выигрыш просто за счет самого кеширования, даже если бы предвыборки не было

boblenin
20.07.2015 18:36Сами элементы либо ссылки, либо простые типы. Почему вы решили что их поместится 8(16) элементов?

tangro
18.07.2015 13:00+1Я так понимаю до понятия «амортизированная сложность операции» исследования не дошли?

jonasas Автор
18.07.2015 13:08-1Амортизированная сложность оценивает последовательность операций над структурой, в моём же случае оценивалась единичная вставка.

tangro
18.07.2015 16:11+1Но ведь ответ на этот вопрос не несёт никакого смысла?

jonasas Автор
18.07.2015 16:16Я не понимаю, как можно работать с амортизированной сложностью в данной ситуации. Если у Вас есть какие-то предложения, поделитесь, пожалуйста. Возможно, я не до конца понимаю смысл этого метода.

Valle
18.07.2015 20:45Амортизированная сложность говорит о том, сколько времени займет вставка в середину N элементов. Если вопрос стоит про единичную операцию то в VM-окружениях ответ простой — там, где нет выделения памяти, и алгоритмическая сложность уже далеко не первостепенна.

areht
18.07.2015 23:47а мы заранее знаем, что надо вставить именно N элементов, или прогоняем алгоритм вставки N раз?
Второй сценарий последний график не покрывает?

tangro
18.07.2015 23:52+2Поскольку во время единичной вставки в ArrayList может произойти переаллокация, а может и не произойти, то единственно возможный вариант ответа о потреблении времени или памяти — «а хрен его знает». Если же речь идёт об оценке «единичных вставок» при том, что они будут происходить в этом массиве миллион раз, скажем, в час — тут уже можно рассуждать об амортизированной сложности по памяти и скорости. И от этого будет толк, поскольку можно оценить использование ресурсов массивом за этот промежуток времени.

vsb
18.07.2015 15:26+7Ваша оценка сложности справедлива для абстрактной машины. В реальном процессоре есть такое понятие, как кеши процессора, работа с которыми происходит гораздо быстрее, чем с памятью.
Связный список в общем случае будет хранить элементы в разбросанном виде (причём в тесте это может не отразиться). Каждый доступ к элементу может потребовать доступа к новому участку памяти. Если у вас 2000 элементов, то проход до 1000 элемента будет занимать 1000 обращений к памяти в худшем случае.
Массив хранит все элементы компактно. 1000 указателей будут занимать 4 килобайта памяти, это вполне влезет в кеш. Поэтому сдвиг будет занимать одно чтение и одну запись в память. Это намного быстрее, чем 1000 обращений к памяти.
В реальной жизни и в вашем тесте элементы связного списка вероятно будут лежать более-менее в одном месте и обращений к памяти будет поменьше, поэтому и разница между массивом и связным списком будет невелика. Но всё может быть.
jonasas Автор
18.07.2015 15:41-7Да, справедливое замечание. Кстати, об этом уже написали выше.
Хотя, я думаю, разница в скорости между ОЗУ и кэшем слишком мала по сравнению со скоростями работы высокоуровневых команд. Но это только лишь моё предположение.
fuCtor
18.07.2015 19:18+3Хотя, я думаю, разница в скорости между ОЗУ и кэшем слишком мала
Ошибаетесь, разница существенна. Это как есть бутерброды с тарелки или бегать за каждым в холодильник, где их еще и найти надо сначала.
mejedi
18.07.2015 20:20Немного конкретики для понимания масштаба; обращение к памяти — это сотни наносекунд. 100 нс — это 100 тактов процессора с частотой 1ггц. То есть один промах мимо кеша стоит как 100 инструкций.
(Disclaimer. Такты в инструкции пересчитывать некорректно, но для грубой оценки сойдет.)
khim
19.07.2015 00:22+1Для грубой оценки лучше использовать вот эту табличку. Вы ошиблись почти на порядок: один промах мимо кеша в память стоит порядка 500 инструкций. Но есть ещё L2. Промахнуться туда не так дорого — порядка 30-40 инструкций. Ваши 100 лежат где-то посередине.

leventov
19.07.2015 01:16С 2009 года память, в отличие от процессоров, все-таки существенно ускорилась. См. комментарий ниже.
Еще, вроде, начинают появляться 128-мегабайтные «L4».
khim
19.07.2015 13:48+3Существенно — это как? В DDR1 на 400MHz цикл самих ячеек был 5ns (но за один цикл байт получить было нельзя), в DDR4 на 4266MHz этот же цикл составляет 3.75ns (можете подсчитать). А ведь время доступа именно этим определяется. Да, ускорение есть — но «копеечное», а с учётом того, что во времена DDR1 вне-JEDECовской самодеятельности было больше — так и совсем нету. L4 на много мегабайт — да, они могут что-то изменить, но пока они ещё мало распространены.

leventov
19.07.2015 15:08Я зацепился за то, что вы упомянули сотни наносекунд, хотя в посте по ссылке упоминается ровно 100. В таблице ниже — 65.

khim
19.07.2015 16:10Я ни про какие сотни наносекунд не говорил. Я говорил про сотни инструкций. Грубо — порядка 500. Но это, конечно, на современных системах с частотой 2-3GHz. А 65ns — да, это характерное время срабатывания памяти. Причём уже давно: модули EDO DRAM для Pentium'а (да-да, того самого, ещё первого) 20 лет назад бывали быстрыми (60ns) и медленными (70ns). Нижеприведённые 65ns лежат как раз посередине :-)
Так что с тех пор ничего в общем-то и не изменилось в смысле задержек. Пропускная способность — выросла многократно и может вырасти ещё, а задержки — плавают слегка то вверх, то вниз, но не более того.
leventov
19.07.2015 16:15обращение к памяти — это сотни наносекунд
Но в целом, убедили.
Edit. А, ну это не вы сказали. Но все равно, 500 — это чересчур большая оценка
khim
19.07.2015 18:11С чего вдруг? Для процессора в 1GHz — да, конечно. Но современные процессоры обычно имеют частоту в 2.5-3GHz (в зависимости от количества ядер) и выполняют по 2-3 инструкции за такт, так что получается где-то от 400 до 600 инструкций за время одного «похода» в память. 500 — хорошее, круглое, число из середины этого интервала.

leventov
19.07.2015 18:16+12-3 инструкции за такт — это идеал, в среднем сильно меньше. 1.33 считается хорошим уровнем: software.intel.com/sites/products/documentation/doclib/iss/2013/amplifier/lin/ug_docs/GUID-5C38FB45-A3ED-41F2-B57C-2B513A666205.htm

mejedi
19.07.2015 10:29Вы ошиблись почти на порядок: один промах мимо кеша в память стоит порядка 500 инструкций.
Ну вообще-то нет :) Обратите внимание, что в коментарии речь идет о процессоре с тактовой частотой 1 ггц.
khim
19.07.2015 13:49Даже процессор в 1GHz исполняет за 1ns всё-таки скорее 2-3 инструкции, а не одну. Но да, я этот момент упустил, каюсь.

vedenin1980
18.07.2015 19:44-2На мой взгляд, вы ошиблись с использованием ArrayList, если речь идет о производительности всегда необходимо указывать максимальное возможное capacity, то есть вместо
arrayList = new ArrayList<>();
надо использовать
arrayList = new ArrayList<>(MAX_SIZE);
в этом случае все замеры производительности по вашему коду у меня показываю что ArrayList работает быстрее (как и ожидалось). Причина в том что любое расширение capacity ArrayList убивает производительность и намного лучше выделить память с запасов (все равно LinkedList требует памяти, как правило, больше), чем допускать увеличения capacity.
Для ArrayList поиск элемента по индексу не составляет труда, так как элементы списка находятся в массиве. Алгоритмическая сложность составляет O(1). В случае LinkedList придётся последовательно перебрать все элементы, пока не доберёмся до нужного элемента. Сложность будет O(n). Вставка в ArrayList связана со сдвигом всех элементов, находящихся после точки вставки, поэтому алгоритмическая сложность этой операции O(n). В LinkedList вставка заключается в создании нового связующего объекта и установки ссылок на него у соседних элементов. Сложность O(1). В сумме сложность вставки в середину у ArrayList и у LinkedList получается одинаковая — O(n).
На самом деле, сложность будет O(n), но у Arraylist будет намного быстрый O(n), для ArrayList поиск по индексу это лишь перемещение указание, а копирование элементов это просто низкоуровневое копирование памяти, что очень быстро. А вот в LinkedList и итерирование медленное и вставка элемента это необходимость проитерироваться к соседнему элементу, поменять кучу указателей, создать новый элемент, что тоже довольно медленно.
Если задача — вставлять элементы в середину в цикле (как делаете это вы в своем тесте), то логично использовать для этой цели LinkedList через ListIterator, так как в этом случае каждая вставка будет O(1).
На самом деле в таком случае для Arraylist проще сделать новый Arraylist, заполнить его и вставить используя addAll(индекс, новый лист) в нужный Arraylist, что все равно окажется более быстрым чем итерироваться ListIterator'ом, а потом вставлять по одному.
P.S. На конференции, один из разработчик Oracla, занимающийся производительностью Java, говорил что практически не существуют реальные кейсы при которых стоит использовать LinkedList вместо Arraylist, то есть в теории они возможны, но на практике практически не встречаются.
vedenin1980
18.07.2015 20:11-1Вообще, надо понимать что по исходному коду Java 8 при добавлении каждого элемента в LinkedList происходит два итерирования на соседние элементы O(2), создание нового объекта (тоже дорогая операция), запись 5 указателей O(5), для добавления нового элемента в Arraylist, происходит запись одной ссылки в указанную область памяти O(1), единственно что может портить картину расширение capacity. А вот копирование областей памяти в массивах это быстрый нативный метод, в отличии от итерирование по ссылкам LinkedList.

mejedi
18.07.2015 20:27+2Вы неправильно используете big-O нотацию, O(5) это то же самое, что и O(1) *по определению*.
Не очень понятно, почему переход по ссылкам должен быть медленный, JIT превратит это в пару машинных инструкций. В общем, ИМХО реализация в Java совсем непричем.

Flammar
18.07.2015 21:53-5Ну, в общем, понятно:
System.arraycopy— операция нативная, так что выполняется практически за O(1) почти вне зависимости от размера массива.
Вообще, интересно: судя по всплескам, операцияnew Object[n], по крайней мере до размера массива 256, выполняется за время O(n)…
leventov
19.07.2015 01:11+4Наоборот: операция new (амортизированно) стоит константу, а arraycopy — O(n).

Flammar
19.07.2015 12:31-1Вот график наводит именно на те мысли, которые я изложил. Вставка в середину, вызывающая
System.arraycopy, оказывается быстрее, чем итерирование по связанному списку. Удвоение размеровArrayList'а оказывается медленнее итерирования по связанному списку — вот что странно.
Правда, посмотрел точнее в код JDK 1.6 — там используется неnew Object[n], что было бы логично, аArray.newInstance, через использованиеArrays.copyOf. Получается, главный тормоз —Array.newInstance, который оказывается медленнее операции, выполняемой за O(n).
leventov
19.07.2015 15:11Array.newInstance это тоже аллокация, это тоже амортизированно O(1). Arrays.copyOf — O(n).

lany
20.07.2015 09:52Вы не туда смотрите, Array.newInstance не используется. Сюда смотрите.

Flammar
21.07.2015 01:48В стандартной JRE «клиентской» версии 1.6.0_26-b03 от Oracle используется, посмотрел декомпилятором. Что используется в HotSpot и OpenJDK — не знаю, не смотрел. Заодно прояснилось, откуда в стандартном JDK используется
Array.newInstanceвместоnew Object[]: неоправдавшийся расчёт на интринсикArrays.copyOf.
lany
21.07.2015 06:19+3Каким ещё декомпилятором? Декомпилятором байткода что ли? О_О Вы думаете, он вам интринсики покажет?

vedenin1980
18.07.2015 21:58-4Вы неправильно используете big-O нотацию, O(5) это то же самое, что и O(1) *по определению*.
Да, на самом деле O(1) вообще писать неправильно, так как в O(...) ожидается функция от n, а любая константа автоматически игнорируется. Это запись исключительно для наглядности, что одно O(n) от другого могут отличаться очень сильно.
Не очень понятно, почему переход по ссылкам должен быть медленный, JIT превратит это в пару машинных инструкций.
Потому что одно дело когда работа идет с непрерывном куском памяти, там переходы быстрые и короткие, другое дело длинный переход в совсем другую страницу памяти.
В общем, ИМХО реализация в Java совсем непричем.
Сильно причем, создание объекта вещь весьма дорогая, а копирование памяти быстрая. Если мы рассматриваем коллекции не с теоретической, а с практической производительности.
Mrrl
19.07.2015 01:49+10O(1) — совершенно корректная запись. Она означает, что существует такая константа C, не зависящая от n, что стоимость нашей операции при любом n не превосходит C.

mejedi
19.07.2015 12:25Не очень понятно, почему переход по ссылкам должен быть медленный, JIT превратит это в пару машинных инструкций.
Потому что одно дело когда работа идет с непрерывном куском памяти, там переходы быстрые и короткие, другое дело длинный переход в совсем другую страницу памяти.
Так дело тут не в джаве а в архитектуре процессора, не так ли?
Вот если бы мы не просто ходили по ссылкам, но еще и меняли их, добавился бы оверхед на обновление служебных структур данных, которые нужны для работы сборщика мусора с поколениями.
Почему кстати создание объекта дорогая операция? Я слышал, что выделение памяти в джаве очень просто устроено (за счет того, что gc имеет возможность двигать объекты в памяти.)
vsb
19.07.2015 14:22+1Выделение памяти устроено очень просто. Только память ещё нужно обнулить после выделения, а обнуление большого куска памяти это (относительно) дорого.
Может быть JIT иногда может понять, что обнулять не нужно, но явно не в 100% случаев.
leventov
19.07.2015 15:13Она обнуляется не в момент выделения, а заранее.

vsb
19.07.2015 17:11Заранее это когда? Где про это можно прочитать?

leventov
19.07.2015 17:28+2Объекты аллоцируются из TLAB до какого-то размера (порядка мегабайта, то есть достаточно большого!), TLAB обнуляется в момент перемещения всего этого TLAB в следующее поколение. (У меня нет ссылки, четко доказывающей этот факт. Но я практически уверен в этом.)
Большие объекты аллоцируются с помощью calloc или чем-то, к нему приближенном. Он делает обнуление. Но с учетом того, что и System.arraycopy, и Arrays.copyOf — интринсики, можно не сомневаться, что лишнего обнуления там никогда нет.
khim
19.07.2015 18:13Как раз для больших объектов
callocне делает обнуления, Он из/dev/zero(или аналога на Windows) странички прихватывает. Их потом «по запросу» обнуляют и выдают, сразу после аллокации там одна и та же страничка растиражирована много раз.
leventov
19.07.2015 18:25+1Это если они прямо из системы идут, mmap/brk. Внутри процесса какой еще /dev/zero.

leventov
19.07.2015 18:30+1А так как Hotspot никогда не отдает память в систему, free() там явно не как munmap реализован, какой бы «ровный» не был размер аллокации

apangin
20.07.2015 00:24+1Непонятно, о чём вы спорите. Очевидно, что при создании объекта в общем случае нужно его обнулить. Причём неважно, когда и кем выполняется обнуление: инлайном в скомилированном коде, при выделении TLAB, во время GC или вообще в ядре ОС. В любом случае, обнулить надо ровно столько, сколько выделяется, не считая заголовка объекта. Таким образом, средняя сложность выделения получается
O(n). Исключения составляют случаи, когда JVM знает, что обнулять не надо, например, вArrays.copyOfилиObject.clone.
Кстати, по умолчанию в HotSpot TLAB не обнуляется, см. опциюZeroTLAB.
Упражнение: догадайся, почему.
leventov
20.07.2015 01:34Это сложность в случае однопоточной машины. А если обнуление где-то в фоне, а параллельном потоке? Или во время перемещения объектов в следующее поколение, причем не добавляя никакой задержки, если бы это было перемещение без обнуления. С помощью каких-то инструкций, которые одновременно с mov зануляют источник (честно, лень смотреть, существуют ли такие).
Во время перемещения мы в любом случае прогоняем весь TLAB через кеш, было бы логично сразу и обнулить. А при аллокации какого-то массива, не факт, что все кеш-лайны понадобятся сразу. (Хотя это слегка надуманный случай).
Исходя из этого я и был уверен, что ZeroTLAB, грубо говоря, включен по умолчанию, а не выключен (конкретно про этот флаг я узнал из твоего комментария, но я имею ввиду, в принципе).
leventov
20.07.2015 01:40Ладно, гипотетическая операция, зануляющая источник, конечно, ничего бы не ускорила, потому что портов записи все равно только два, но аргумент про «фон» остается

apangin
20.07.2015 02:33+1Нет такого понятия как однопоточная или многопоточная сложность. Алгоритмическая сложность — она одна. Параллелизация может сократить время лишь в константное число раз, но никогда не сделает
O(1)изO(n).
Если даже обнулением занимается фоновый поток, если даже операция совмещена с другой, всё равно, количество работы, которое нужно выполнить, кратноn. Пусть потокmainу тебя сверхбыстрый, но если фоновых вычислений ассимптотически больше, это значит, что в какой-то моментmainпросто будет вынужден остановиться, чтобы дождаться другого потока.

nhekfqn
18.07.2015 22:07-3Корректно ли говорить, что вставка в ArrayList — это O(n)? Массив при сдвиге копируется целиком, а не поэлементно. Как влияет размер копирумого массива на скорость копирования? На сколько я понимаю скопировать массив из 2-х элементов не в 2 раза медленнее, чем массив из одного элемента. Скопировать 10 мб медленее, чем 10 байт, но в не миллион раз. Я всегда думал, что падением скорости можно пренебречь и сложность этой операции O(1), кто-нибудь сможет дать более точный ответ?

vedenin1980
18.07.2015 22:25Проблема ответа на вопрос в том что System.arraycopy() это нативный метод, то есть напрямую зависит от реализации конкретной платформы. В целом, в большинстве платформ это скорее всего все-таки O(n), но очень быстрый O(n). Судя по perfomance тестам в инете от 2 до 20 раз более быстрый чем ручное копирование массивов. Но точного ответа для всех ОС вряд ли можно получить.

leventov
19.07.2015 01:06-1Судя по perfomance тестам в инете от 2 до 20 раз более быстрый чем ручное копирование массивов.
Судя по хорошим, свежим тестам, оно даже помедленнее, чем ручное… psy-lob-saw.blogspot.ru/2015/04/on-arraysfill-intrinsics-superword-and.html
vedenin1980
19.07.2015 15:41+2Забавно, и при этом дать ссылку на статью где утверждается ровно противоположенное…
ArrayFill.copyBytes 1300.313 ± 13.482 ns/op
ArrayFill.manualCopyBytes 1477.442 ± 13.030 ns/op
…
Use System.arrayCopy, it is better than your handrolled loop. But surprisingly not hugely better, hmmm.
leventov
19.07.2015 16:14+2Да, проглядел. Но это все равно опровергает ваши «2-20 раз». А Array.fill вообще медленнее ручного, правда, всего на константочку.

vedenin1980
19.07.2015 18:45Нет, не опровергает, только показывает что у автора теста на его конфигурации (Oracle JDK8u40/i7-4770@3.40GHz/Ubuntu) выигрываешь только 14%, однако по этому нельзя судить о всех конфигурациях. По-хорошему, только замеры производительности нативных методов на разных ОС/процессорах/JDK могут показать хоть что-то определенное.

leventov
19.07.2015 18:54+1Дело совершенно точно не в ОС, и не в конкретных (относительно современных) x86 процессорах, для которых, начиная с некоторой версии (скорее всего, одно из обновлений семерки), Hotspot JVM умеет оптимизировать ручное копирование в практически то же самое, что System.arraycopy. Двумя, а тем более двадцатью разами разницы там уже не пахнет.
Ну, на ARM еще может быть по-другому

vedenin1980
19.07.2015 18:59Да и размер массива в тестах, которые вы показывали, был всего 32K, то есть всего 4 тыс ссылок, а это слишком мало чтобы делать такие выводы (особенно учитывая что вызов нативного метода вовсе не «бесплатен»), производительность копирования в первую очередь важна при копировании сотен тысяч и миллионов элементов, а вот тут нативные методы копирования должны показывать себя лучше (однако я не могу утверждать что абсолютно при любой конфигурации). По-хорошему мерить копирование при 4 тыс. элементов большого смысла нет, кстати при копировании массива из 10-100 элементов нативные методы вроде даже проиграют, ибо затраты на нативность перевешивают собственно затраты на копирование.

leventov
20.07.2015 00:05+1System.arraycopy это интринсик, вместо которого JVM аккуратно подставляет SIMD-инструкцию. Хоть он и объявлен native, никаких затрат на нативность он не несет

vsb
18.07.2015 22:38+1O(n) это не значит, что в 2 раза медленнее. Даже если массив из 2-х элементов копируется в 1.001 раза медленней, чем массив из 1 элемента. это уже O(n).
На практике массивы копируются со ступенчатой скоростью. Грубо говоря от 0 до 16 байтов копируются за n тактов, от 17 до 32 байтов за 2n тактов и тд. Но это очень грубая прикидка, конечно.
Но алгоритмическая сложноcть копирования массива из N элементов это O(N).
Mrrl
19.07.2015 01:56+4Даже если массив из 2-х элементов копируется в 1.001 раза медленней, чем массив из 1 элемента. это уже O(n).
Это вообще ничего не значит. Массив из двух элементов может копироваться в 10 раз быстрее, чем из 1 элемента, и при этом сложность быть O(n!).
Чтобы получить какую-то эмпирическую оценку сложности, надо сравнивать времена при больших сильно расличающихся n. Например, 1000 и 1000000. Если 1000 элементов копируется вдвое быстрее, чем 1000000, значит, сложность, вероятно, O(log(n)). Если в 30 раз быстрее — похоже на O(sqrt(n)). Если в миллион раз — то O(n^2), и вероятно, копирование реализовано на машине Тьюринга…

Flammar
21.07.2015 02:09Если ещё раз внимательнее взглянуть на график, то модно увидеть, что в использованной автором JVM (скорее всего это стандартная JVM от Oracle, раз JVM не указана) в благоприятном случае копирование половины массива через нативный метод занимает по времени почти стабильно 0,6-0,65 от итерирования по половине списка, а реаллокация через рефлексивный метод (в предположении что это стандартная JVM от Oracle) плюс копирование всего массива через нативный метод — в 1,5-1,9 раза медленнее, чем итерирование по половине массива.



Aivean
Очень экзотичный сценарий вы выбрали для исследования.
Если задача — единожды вставить элемент в середину списка, то, по сути, не важно, какая реализация списка используется — обе операции будут O(n).
Если задача — вставлять элементы в середину в цикле (как делаете это вы в своем тесте), то логично использовать для этой цели LinkedList через ListIterator, так как в этом случае каждая вставка будет O(1).
Если же задача предполагает вставку элементов в разные «случайные» места по сложной логике, то, опять же, логично будет за один проход расчитать будущие позиции, затем создать на их основе новый список (примерно как это делается при сортировке подсчетом).
jonasas Автор
Вопрос на собеседовании подразумевал разовую вставку именно в самую середину, поэтому я не могу воспользоваться ListIterator. А в цикле я вставлял данные, пытаясь показать, что многократное увеличение размера массива у ArrayList снижает производительность относительно LinkedList.
edwardoid
Вы, наверное, еще подразумеваете что длина списка 2n? Вставить-то надо в середину.
lany
Если надо вставить много элементов, то в обоих случаях логичнее использовать addAll. Это будет быстрее, чем мучать киску по одному элементу.
Mrrl
Это если, во-первых, все элементы известны заранее, во-вторых, для каждого из них известно место, куда его надо вставить, и в-третьих, эти места идут подряд. Даже если надо просто вставить k элементов в середину массива из n элементов, итоговый порядок окажется довольно причудливым — ведь после вставки очередного элемента массив станет длиннее, и середина сместится.