В точном компьютерном и физическом моделировании нуждается любой инженер, особенно если компания хочет создать самый износостойкий и прочный подшипник, его свойства окружность и параметры должны быть известны, чуть ли не до уровня атома.
Представьте, вы даёте задачу программисту найти точный процент и модель соприкосновения подшипника, и оказывается что это невозможно, так как и невозможно смоделировать точную окружность. Как и невозможно смоделировать точную площадь соприкосновения.
Понятие круга является одним из универсальных математических понятий, дословно обобщаемым на случай произвольных метрических пространств. Но в разделе информатики, эта тема очень редко поднимается потому что до невозможности сложна.
Так что такое круг? И почему его точная математическая модель невозможна.

В научном понимании круг это правильный 65537 угольник (шестьдеся?тпятьты?сячпятисо?ттридцатисемиуго?льник) — правильный многоугольник с 65 537 углами и 65 537 сторонами.
Значит для программиста круг это многоугольник с 65 537 углами — и эти углы будут соприкасаться с плоской поверхностью или такой же окружностью, и меняя равновесие всего это математического круга с 65 537 углами. Согласитесь что модель уже устарела?
Гауссом в 1796 году было доказано, что правильный n-угольник можно построить циркулем и линейкой, если нечётные простые делители n являются различными числами Ферма. В 1836 году П. Ванцель доказал, что других правильных многоугольников, которые можно построить циркулем и линейкой, не существует. Ныне это утверждение известно как теорема Гаусса — Ванцеля.
Могу даже открыть секрет настолько узкий в отрасли подшипников, что большинство автомобильных, железнодорожных и авиа катастроф происходит именно по причине некачественных подшипников так как проверить качество и окружность порой невозможно так как наука работает в основном не с числами а «диапазонами» то и процент брака в подшипниковой индустрии из-за проблемы создания идеально ровного подшипника самый высокий.
Такую проблему мы наблюдаем и в играх
Точность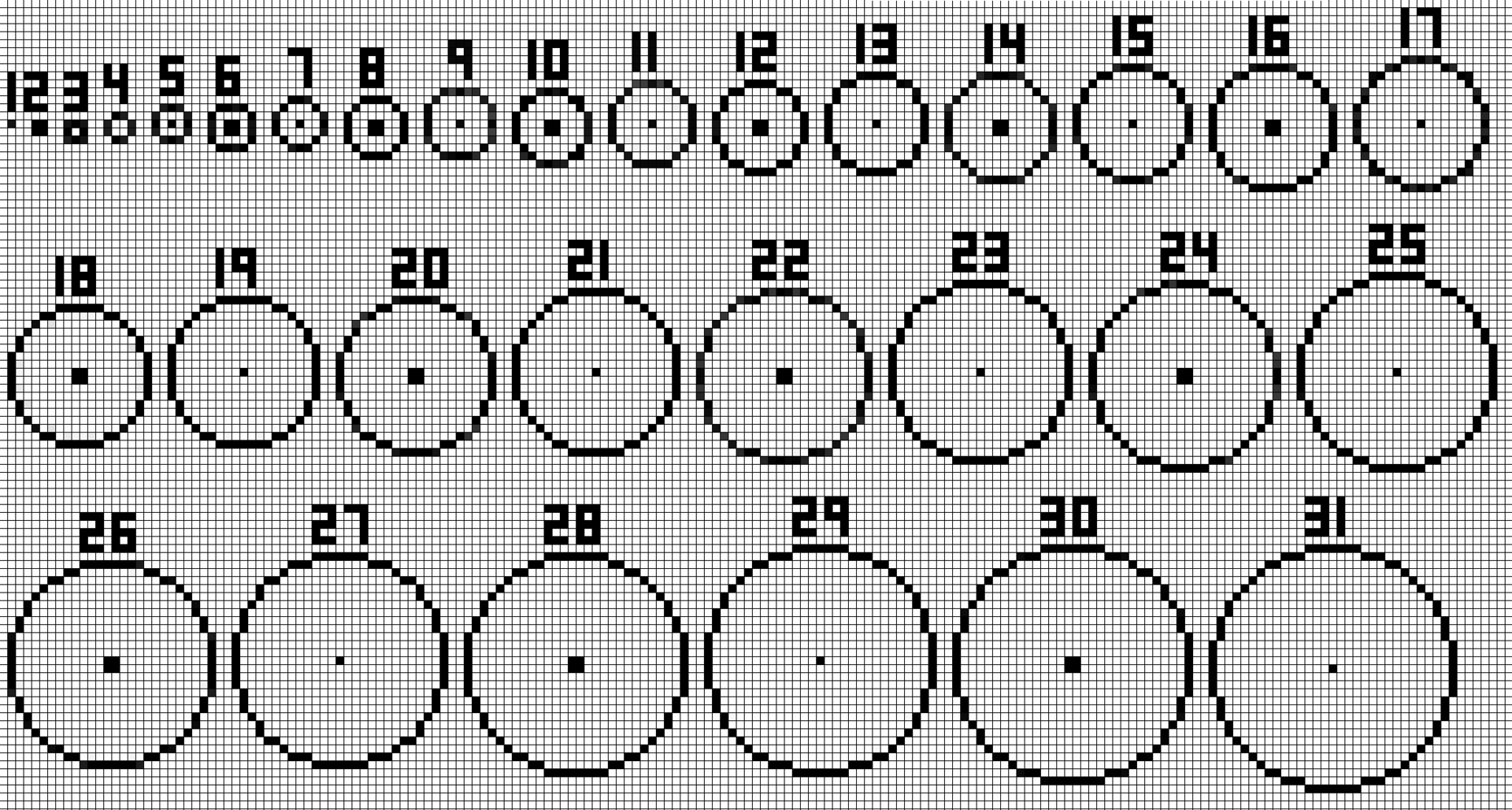

И эта точность очень низкая.
А 65 тысяч углов у круга это меньше миллиона.

Но даже и это не предел. Идеальный круг вообще бесконечен (имеет бесконечное количество углов). Как тогда его выразить в программировании, если любое число будет его неточной моделью? Или уже такая высокая точность будет ненужна? Ведь в любом массовом моделировании иза мельчайшей детали образуются каскадные лавинообразные эффекты которые дают разные результаты.
Спасибо за внимание.


androidovshchik
Как теперь жить то, если даже круг это n-угольник)?
addewyd
Только не для программиста.
BubaVV
Что я только что прочитал?
justhabrauser
Бредятину.
Наблюдаем рождение нового «Редактора GT».
Поколения ЕГЭ.
dima_mendeleev
> Как тогда его выразить в программировании, если любое число будет его неточной моделью?
А как его выразить вообще, не в программировании, кроме как на словах?
hurtavy
есть же точные формулы…
dima_mendeleev
Формулы — это и есть на словах.
T_Sun
например в коде
dima_mendeleev
Ведь
X,X0,… ограничены (типfloatограничен или банально память ограничена).В результате все равно получится многоугольник, хоть и с очень большим количеством углов.
AlexTOPMAN
Храните тогда результат не значением, а формулой. И не будет ограничения. И вообще, зачем вам точность, превышающая ваши расчётные возможности? Идеальность круга как раз в том, чтобы наоборот — без нужды не идеализировать его поверхность. Вам не кажется?..
dima_mendeleev
Это не имеет отношения к моему комментарию.
Sirion
Так толсто, что даже тонко.
akura13
Circle circle = new Circle();
circle.setCenterX(100.0f);
circle.setCenterY(100.0f);
circle.setRadius(50.0f);
Akon32
Что?? Точные математические модели круга — это, в зависимости от задачи:
1) неравенство (x-c_x)^2 + (y-c_y)^2 <= r^2 в двумерной плоскости.
2) радиус r круга (или диаметр d);
3) радиус r и координаты центра С;
Можно придумать ещё варианты.
Что вы имеете в виду под этим вашим "научным пониманием"?
Tsvetik
Что за хрень я только что прочитал?
Инженер, моделирующий механические системы должен знать хотя бы основы сопромата, касающиеся упругостей и деформаций.
nerudo
У вас просто система координат неправильная ;)
vilgeforce
А дальше-то что? Резко перестать считать что угодно круглым?
iliazeus
В дополнение к предыдущим комментаторам, напомню о существовании символьных вычислений.
KvanTTT
Да в принципе ничего идеального не существует. А в математическом мире все идеально, значит математики не существует!!!
Дополню предыдущих комментаторов: в физических движках круги и шары просчитываются аналитически. Это, кстати, намного уменьшает количество необходимых вычислений.
zzzmmtt
Идеальным бывает газ, но только в учебнике физики.
mskotyn
Автору курить курсы металловедения, металлообработки, материаловедения и сопромата любого технического вуза. Желательно самому посмотреть в микроскоп на образцы сталей с крупно- и мелкозернистой, игольчатой структурами. Разобраться с линейным тепловым расширением, упругими деформациями и их влиянием на геометрию детали.
nerudo
PS За «квадрат с 65 537 углами» — отдельный приз!
masai
Просто многие углы совпадают.
Ascar
Если бы было 65536, то возможно гиперкуб в 16 мерном пространстве.
amarao
Представим себе окружность C с диаметром D. Устремим D к планковой длине. Построим хорду H таким образом, чтобы длина отрезка окружности была D. Что находится внутри H?
Ascar
> Так что такое круг?
Круг
dom1n1k
Подозреваю, что тут замешан гладиолус
pallada92
Может быть автор добавил статью в песочницу к 1 апреля, но её только сейчас одобрили?
KvanTTT
Ну не ждать же еще год до следующего 1 апреля :D
mastan
В математике круг — геометрическое место точек, расположенных не далее определённой константы(радиуса) от выбранной точки(центра).
Окружность — геометрическое место точек, расположенных на удалении радиуса.
Если автор решил аппроксимировать круг N-угольником, ничего плохого в этом нет, но надо чётко говорить — это аппроксимация N-угольником, а не окружность.
Если деталь обтачивают на токарном станке, там никаких 65537-угольников тоже нет. Может будет N-угольник… хотя нет, N мало, возьмём M. Будет несколько неправильный M-угольник.
Теоретический предел приближения к окружности в реальной жизни — «растеризация» на уровне атомов.
Ascar
Учитывая, что подшипник это сфера или конус, то говорить о многоугольнике вообще смысла нет…
ksbes
Никто не мешает каким-нибудь электронам бегать по кругу в магнитном поле, образуя тем самым абсолютно круглую (ну, может, немного овально-волновую, но всё же гладкую — без углов) поверхность.
BubaVV
Волновая природа электрона, конечно же
akhalat
> Окружность — геометрическое место точек, расположенных на удалении радиуса.
геометрическое место ВСЕХ точек :)
по широко распространенной легенде, так валили всех «неугодных» при поступлении в МГУ
Sychuan
Что-то не совсем понимаю. Что значит всех? В смысле мне кажется это не добавляет ничего в определение.
ksbes
отсутствие этого слова даёт возможность интерпретировать определение как геометрическое место некоторых точек.
Т.е. хочешь — не хочешь, но если ты — точка и оказался на этом расстоянии от центра, то ты ОБЯЗАН быть частью окружности. А так кажется, что есть выбор
akhalat
> Что-то не совсем понимаю. Что значит всех? В смысле мне кажется это не добавляет ничего в определение.
Когда говорят, что окружность — прсто множество точек, расположенных на заданном расстоянии от заданной точки, то можно взять грубо говоря 4 точки и они будут удовлетворять этому определению. Поэтому, формально, правильно говорить ВСЕХ.
Естественно, обычно преподаватели относились к такому с пониманием и не снижали оценку, но вот когда надо было «завалить» абитуриента и «не поступить», в ход шли и такие низенькие средства.
Ascar
А можно взять и не 4. Из того что ваше множество содержит нужных 4 точки следует что оно подходит под определение, но не обратно.
akhalat
> Из того что ваше множество содержит нужных 4 точки следует что оно подходит под определение
Ну как бы в этом и проблема определения без слова «всех».
Ascar
Тут не проблемы, следствие в одну сторону выполняется у вас просто. Вы сами же сказали что если 4 точки таких то, то подходит под данное определение. Но из определения не следует что точки всего 4.
akhalat
Определение не может работать «в одну сторону», а если под «определение» окружности попадает что-то, не являющееся окружностью, то «определение» — неверно.
> Но из определения не следует что точки всего 4.
Из определения следует, что точек может быть и 4, и 3, и 2.
VanKrock
Не точное определение, к которому не верно применять такое дополнение, породило спор в котором сложно прийти к истине, так как каждый в чем-то прав, так не прав, так как не верный сам тезис спора. Приведу цитату из википедии, которая в свою очередь ссылается на Математическую энциклопедию 1984 года:
В данном определении действительно можно было упустить достаточно важное слово «всех». Добавление же слова «всех» в определение данное mastan которое в этом случае будет: делает его еще более запутанным и не понятным и как минимум порождает вопрос «Всех точек чего?»akhalat
тем не менее, у человека не возникло вопроса: «точек чего?», но, как кажется, он до сих пор не поверил зачем там нужно слово «всех»
так что про «более запутанное и непонятное» вы, мягко говоря, не правы
ну и в чём я не прав, в том, что при использовании подобных определений обязательно указывать слово «всех»?
я сделал акцент на слове ВСЕХ, т.к. именно оно содержало всю суть истории, дальше «улучшать» то определение у меня и задачи не было, а было задача добавить хоть какого-то интересного материала, который можно придумать про банальную окружность, к достаточно никчемной статье.
или вы действительно думаете, что написав я «всех точек плоскости» у человека не возникло бы его непонимания? как бы вы его тогда уже выгораживали?
VanKrock
А вот и нет. Использование слова «всех» будет корректно в определении:
Употребление слова «всех» будет НЕ корректно в определении:
По той причине, что здесь используется термин «Геометрическое место точек (ГМТ)» и коверкать его и пытаться превратить в какой-нибудь «ГМВТ» не нужно.
akhalat
https://www.google.ru/search?q="геометрическое+место+всех+точек"в частности, например, так написано в книге «Курант, Роббинс. Что такое математика? перевод под ред. Колмогорова»
так что уточнение ВСЕХ — вполне допустимо, когда надо подчеркнуть, что должны входить именно все точки. для чего оно мной было и использовано, причём в формате короткой ремарки
и к развившейся так называемой «дискуссии» это «геометрическое место» отношение имело слабое, и вообще-то с самого ее начала я перешел на определение «множество равноудаленных точек». там человек, в частности, не понимал, что плохого в определении, под которое подходят контр-примеры: дескать, оно ведь всё равно работает «в одностороннем порядке»
VanKrock
Оно бессмысленно, но если вы любитель масла масленного тогда ладно
akhalat
вы хоть вспомните контекст, в котором я его первоначально привёл
> тогда ладно
ну с Колмогоровым вам, наверное, трудновато будет поспорить
Ascar
Вы так и не ответили на habr.com/ru/post/447702/#comment_20016314
Попробую еще проще объяснить. Из того определения следует что точек, по вашему, оказывается может быть не только 4, а еще 3 и 2, и под них определение верно по вашему. Так выходит что какую бы точку удовлетворяющую условию вы бы не взяли определение так же будет верным.
Ascar
Ага, если нет ограничения то множество шире.
Ascar
А всех это откуда?
«Окружностью называется совокупность точек плоскости, равноудаленных от
фиксированной точки, называемой ее центром.»
emmibox
Лучшие прочностные модели дают результаты с погрешностями хорошо если в единицах % а износостойкость и в 10-ках% не особо посчитать — и это проблема полноты самих моделей и исходных знаний об объекте моделирования, а не точности вычисления кругов в них… В подшипниках коэффициенты запасов прочности обычно так от двоечки начинаются, а там где люди могут пострадать — от троечки и поболее… Смело округляй Pi до трех — суть не поменяется! И соприкосновений там нет и быть не может. Если они будут — подшипник сварится.
bopoh13
trofimovep
Монитор не может нарисовать идеально закругленные линии, значит все учебники математики можно выбрасывать…
Иииии, видимо тут имеется ввиду не круг, а окружность.
И как быть с окружностями других размерностей? Например, S^0 — две точки, их тоже не существует? Или две точки — это 15276-угольник?
solariserj
> Монитор не может нарисовать идеально закругленные линии
А толку, даже если бы и мог, вы не сможете это увидеть — количество колбочек на сетчатке ограничено
Jolt
неужели для аудитории хабра это на столько не очевидная вещь, что необходимо прикладывать поясняющую картинку?
Oz_Alex
Просто носитель тайного знания настолько уверен в своей избранности, что думает даже такие вещи неизвестны широкой аудитории.
alex103
«Идеального математического круга не существует»
Не существует где?
В идеальном математическом мире — точно существует!
В остальных мирах — существует по необходимости. (наверное)
Вот эта необходимость и определяет уровень «идеальности».
Вообще народ зря минусует!
Эту статью можно разобрать на цитаты!
:-)
(тут должна быть знаменитая картинка с подписью: Нельзя так просто взять и посчитать количество углов круга!)
Jogger
Ядерная бомба всегда попадает в эпицентр. (с)
ANIDEANI Автор
Надо было добавить в статью изображение.

И дать новое определение «замкнутое равномерное бесконечное многоугольное пространство»
dima_mendeleev
Большое Вам спасибо за статью! Пусть она не имеет большой ценности для аудитории Хабра, но философскую ценность она безусловно имеет, поскольку важно осознавать, что простые и привычные нам вещи, которыми мы оперируем/аргументируем каждый день, на самом деле теоретичны, то есть не имеют реальных практических примеров. А что говорить о чем нибудь более сложном.