Привет, Хабр! Представляю вашему вниманию перевод статьи «Image Similarity using Deep Ranking» автора Akarsh Zingade.
Понятия "сходства двух изображений" — введено не было, поэтому давайте введем данное понятие хотя бы в рамках статьи.
Сходство двух изображений — это результат сравнения двух изображений по определенным критериям. Его количественная мера определяет степень сходства между диаграммами интенсивности двух изображений. С помощью меры сходства сравниваются какие-то признаки, описывающие изображения. В качестве меры сходства обычно применяется: расстояние Хемминга, евклидово расстояние, расстояние Манхэттена и т. д.
Deep Ranking — изучает мелкозернистое сходство изображений, характеризуя тонкодисперсное отношение сходства изображений с помощью набора триплетов.
Триплет содержит изображение запроса, положительное и отрицательное изображение. Где положительное изображение больше похоже на изображение запроса нежели, чем отрицательное.
Пример набора триплетов:

Первая, вторая и третья строка соответствует изображению запроса. Вторая строка (положительные изображения) больше похоже на изображения запроса нежели, чем третья (отрицательные изображения).
Сеть состоит из 3 частей: триплетной выборки, ConvNet и слой ранжирования.
Сеть принимает триплеты изображений в качестве входных данных. Один триплет изображения содержит изображение запроса , положительное изображение и отрицательное изображение , которые независимо передаются в три идентичные глубокие нейронные сети.
Самый верхний слой ранжирования — оценивает функцию потери триплетов. Эта ошибка корректируется в нижних слоях для того, чтобы свести к минимуму функцию потери.
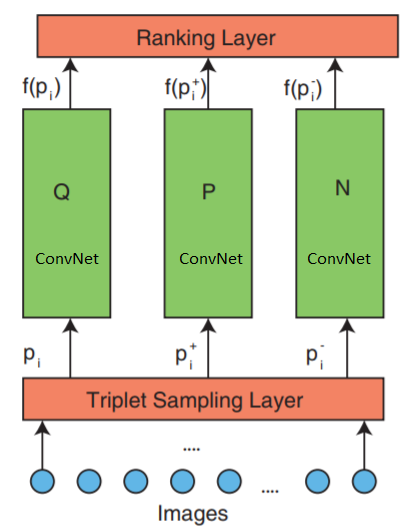
Давайте теперь более детально рассмотрим средний слой:
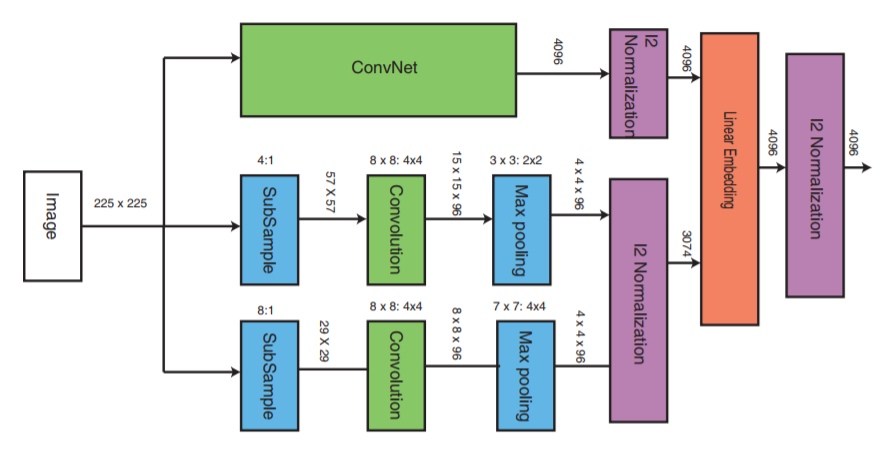
ConvNet может являться любой глубокой нейронной сетью (в рамках данной статьи будет рассматриваться одна из реализации сверточной нейронной сети VGG16). ConvNet содержит сверточные слои, слой максимального пула, слои локальной нормализации и полносвязные слои.
Две другие части получают изображения с пониженной частотой дискретизации и проводят этап свертки и макс пулинга. Далее происходит этап нормализации трех частей и в конце происходит объединение их с линейным слоем с последующей нормализацией.
Есть несколько путей для формирования триплет файла, например, использовать экспертную оценку. Но в данной статье будет использоваться такой алгоритм:
Цель состоит в том, чтобы обучить функцию, которая назначает маленькое расстояние для наиболее похожих изображений и большое для разных. Это может быть выражено как:
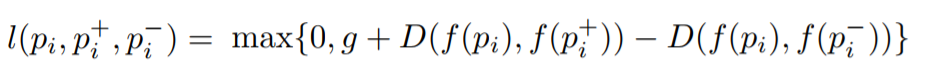
Где l – коэффициент потери для триплетов, g – коэффициент разрыва между между расстоянием двух пар изображений: (, ) и (, ), f — embedding функция, которая отображает изображение в вектор, — это изображение запроса, — это положительное изображение, — это отрицательное изображение, а D — это евклидово расстояние между двумя евклидовыми точками.
Реализация с помощью Keras.
Используются три параллельные сети для запроса, положительного и отрицательного изображения.
В реализации есть три основные части, это:
Обучение трех параллельных глубоких сетей будет затрачивать много ресурсов памяти. Вместо трех параллельных глубоких сетей, которые принимают изображение запроса, положительное и отрицательное изображение, на вход нейронной сети будут подаваться эти изображения последовательно в одну глубокую нейронную сеть. Тензор, переданный на слой потерь, будет содержать вложение изображения в каждом ряду. Каждая строка соответствует каждому входному изображению в пакете. Поскольку, последовательно передается изображение запроса, положительное изображение и отрицательное изображение, первая строка будет соответствовать изображению запроса, второе — положительному изображению, а третье — отрицательному изображению, а затем повторяется до конца пакета. Таким образом, в слой ранжирования получает вложение всех изображений. После этого вычисляется функция потери.
Чтобы реализовать слой ранжирования, нам понадобится написать собственную функцию потери, которая будет вычислять евклидово расстояние между изображением запроса и положительным изображением, а также евклидово расстояние между изображением запроса и отрицательным изображением.
Размер пакета всегда должен быть кратным 3. Поскольку триплет содержит 3 изображения, а триплетные изображения передаются последовательно (мы отправляем каждое изображения глубокую нейронную сеть последовательно)
Остальной код по ссылке
Алгоритм Deep Ranking
Понятия "сходства двух изображений" — введено не было, поэтому давайте введем данное понятие хотя бы в рамках статьи.
Сходство двух изображений — это результат сравнения двух изображений по определенным критериям. Его количественная мера определяет степень сходства между диаграммами интенсивности двух изображений. С помощью меры сходства сравниваются какие-то признаки, описывающие изображения. В качестве меры сходства обычно применяется: расстояние Хемминга, евклидово расстояние, расстояние Манхэттена и т. д.
Deep Ranking — изучает мелкозернистое сходство изображений, характеризуя тонкодисперсное отношение сходства изображений с помощью набора триплетов.
Что такое триплет?
Триплет содержит изображение запроса, положительное и отрицательное изображение. Где положительное изображение больше похоже на изображение запроса нежели, чем отрицательное.
Пример набора триплетов:

Первая, вторая и третья строка соответствует изображению запроса. Вторая строка (положительные изображения) больше похоже на изображения запроса нежели, чем третья (отрицательные изображения).
Сетевая архитектура Глубокого ранжирования
Сеть состоит из 3 частей: триплетной выборки, ConvNet и слой ранжирования.
Сеть принимает триплеты изображений в качестве входных данных. Один триплет изображения содержит изображение запроса , положительное изображение и отрицательное изображение , которые независимо передаются в три идентичные глубокие нейронные сети.
Самый верхний слой ранжирования — оценивает функцию потери триплетов. Эта ошибка корректируется в нижних слоях для того, чтобы свести к минимуму функцию потери.

Давайте теперь более детально рассмотрим средний слой:

ConvNet может являться любой глубокой нейронной сетью (в рамках данной статьи будет рассматриваться одна из реализации сверточной нейронной сети VGG16). ConvNet содержит сверточные слои, слой максимального пула, слои локальной нормализации и полносвязные слои.
Две другие части получают изображения с пониженной частотой дискретизации и проводят этап свертки и макс пулинга. Далее происходит этап нормализации трех частей и в конце происходит объединение их с линейным слоем с последующей нормализацией.
Формирование триплетов
Есть несколько путей для формирования триплет файла, например, использовать экспертную оценку. Но в данной статье будет использоваться такой алгоритм:
- Каждое изображение в классе формирует изображение запроса
- Каждое изображение, кроме изображения запроса, будет формировать положительное изображение. Но можно ограничить количество положительных изображений для каждого изображения запроса
- Отрицательное изображение случайно выбирается из любого класса, который не является классом изображения запроса
Функция потери триплетов
Цель состоит в том, чтобы обучить функцию, которая назначает маленькое расстояние для наиболее похожих изображений и большое для разных. Это может быть выражено как:
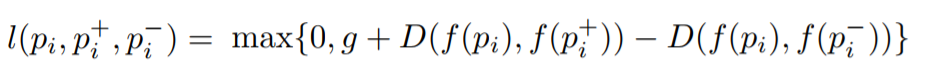
Где l – коэффициент потери для триплетов, g – коэффициент разрыва между между расстоянием двух пар изображений: (, ) и (, ), f — embedding функция, которая отображает изображение в вектор, — это изображение запроса, — это положительное изображение, — это отрицательное изображение, а D — это евклидово расстояние между двумя евклидовыми точками.
Реализация алгоритма Deep Ranking
Реализация с помощью Keras.
Используются три параллельные сети для запроса, положительного и отрицательного изображения.
В реализации есть три основные части, это:
- Реализация трех параллельных многомасштабных нейронных сетей
- Реализация функции потери
- Генерация триплетов
Обучение трех параллельных глубоких сетей будет затрачивать много ресурсов памяти. Вместо трех параллельных глубоких сетей, которые принимают изображение запроса, положительное и отрицательное изображение, на вход нейронной сети будут подаваться эти изображения последовательно в одну глубокую нейронную сеть. Тензор, переданный на слой потерь, будет содержать вложение изображения в каждом ряду. Каждая строка соответствует каждому входному изображению в пакете. Поскольку, последовательно передается изображение запроса, положительное изображение и отрицательное изображение, первая строка будет соответствовать изображению запроса, второе — положительному изображению, а третье — отрицательному изображению, а затем повторяется до конца пакета. Таким образом, в слой ранжирования получает вложение всех изображений. После этого вычисляется функция потери.
Чтобы реализовать слой ранжирования, нам понадобится написать собственную функцию потери, которая будет вычислять евклидово расстояние между изображением запроса и положительным изображением, а также евклидово расстояние между изображением запроса и отрицательным изображением.
Реализация функции расчета потерь
_EPSILON = K.epsilon()
def _loss_tensor(y_true, y_pred):
y_pred = K.clip(y_pred, _EPSILON, 1.0-_EPSILON)
loss = tf.convert_to_tensor(0,dtype=tf.float32) # initialise the loss variable to zero
g = tf.constant(1.0, shape=[1], dtype=tf.float32) # set the value for constant 'g'
for i in range(0,batch_size,3):
try:
q_embedding = y_pred[i+0] # procure the embedding for query image
p_embedding = y_pred[i+1] # procure the embedding for positive image
n_embedding = y_pred[i+2] # procure the embedding for negative image
D_q_p = K.sqrt(K.sum((q_embedding - p_embedding)**2)) # calculate the euclidean distance between query image and positive image
D_q_n = K.sqrt(K.sum((q_embedding - n_embedding)**2)) # calculate the euclidean distance between query image and negative image
loss = (loss + g + D_q_p - D_q_n ) # accumulate the loss for each triplet
except:
continue
loss = loss/(batch_size/3) # Average out the loss
zero = tf.constant(0.0, shape=[1], dtype=tf.float32)
return tf.maximum(loss,zero)Размер пакета всегда должен быть кратным 3. Поскольку триплет содержит 3 изображения, а триплетные изображения передаются последовательно (мы отправляем каждое изображения глубокую нейронную сеть последовательно)
Остальной код по ссылке
Список литературы
[1] Object Recognition from Local Scale-Invariant Features- www.cs.ubc.ca/~lowe/papers/iccv99.pdf
[2] Histograms of Oriented Gradients for Human Detection- courses.engr.illinois.edu/ece420/fa2017/hog_for_human_detection.pdf
[3] Learning Fine-grained Image Similarity with Deep Ranking- static.googleusercontent.com/media/research.google.com/en//pubs/archive/42945.pdf
[4] ImageNet Classification with Deep Convolutional Neural Networks- papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf
[5] Dropout: A Simple Way to Prevent Neural Networks from Overfitting- www.cs.toronto.edu/~hinton/absps/JMLRdropout.pdf
[6] ImageNet: A Large-Scale Hierarchical Image Database- www.image-net.org/papers/imagenet_cvpr09.pdf
[7] Fast Multiresolution Image Querying- grail.cs.washington.edu/projects/query/mrquery.pdf
[8] Large-Scale Image Retrieval with Compressed Fisher Vectors- citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.401.9140&rep=rep1&type=pdf
[9] Beyond Bags of Features: Spatial Pyramid Matching for Recognizing Natural Scene Categories- ieeexplore.ieee.org/document/1641019
[10] Improved Consistent Sampling, Weighted Minhash and L1 Sketching- static.googleusercontent.com/media/research.google.com/en//pubs/archive/36928.pdf
[11] Large scale online learning of image similarity through ranking- jmlr.csail.mit.edu/papers/volume11/chechik10a/chechik10a.pdf
[12] Learning Fine-grained Image Similarity with Deep Ranking- users.eecs.northwestern.edu/~jwa368/pdfs/deep_ranking.pdf
[13] Image Similarity using Deep Ranking- medium.com/@akarshzingade/image-similarity-using-deep-ranking-c1bd83855978
[2] Histograms of Oriented Gradients for Human Detection- courses.engr.illinois.edu/ece420/fa2017/hog_for_human_detection.pdf
[3] Learning Fine-grained Image Similarity with Deep Ranking- static.googleusercontent.com/media/research.google.com/en//pubs/archive/42945.pdf
[4] ImageNet Classification with Deep Convolutional Neural Networks- papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf
[5] Dropout: A Simple Way to Prevent Neural Networks from Overfitting- www.cs.toronto.edu/~hinton/absps/JMLRdropout.pdf
[6] ImageNet: A Large-Scale Hierarchical Image Database- www.image-net.org/papers/imagenet_cvpr09.pdf
[7] Fast Multiresolution Image Querying- grail.cs.washington.edu/projects/query/mrquery.pdf
[8] Large-Scale Image Retrieval with Compressed Fisher Vectors- citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.401.9140&rep=rep1&type=pdf
[9] Beyond Bags of Features: Spatial Pyramid Matching for Recognizing Natural Scene Categories- ieeexplore.ieee.org/document/1641019
[10] Improved Consistent Sampling, Weighted Minhash and L1 Sketching- static.googleusercontent.com/media/research.google.com/en//pubs/archive/36928.pdf
[11] Large scale online learning of image similarity through ranking- jmlr.csail.mit.edu/papers/volume11/chechik10a/chechik10a.pdf
[12] Learning Fine-grained Image Similarity with Deep Ranking- users.eecs.northwestern.edu/~jwa368/pdfs/deep_ranking.pdf
[13] Image Similarity using Deep Ranking- medium.com/@akarshzingade/image-similarity-using-deep-ranking-c1bd83855978

