Преобразование черно-белых изображений в ASCII-графику при помощи неотрицательного матричного разложения / forpes.ru

Главная
Преобразование черно-белых изображений в ASCII-графику при помощи неотрицательного матричного разложения

Преобразование черно-белых изображений в ASCII-графику при помощи неотрицательного матричного разложения +58

10.08.2019 18:05

Muttnik 19 8900 Источник

В общем случае преобразование изображения в ASCII-графику представляет собой довольно трудоемкую задачу, однако существуют алгоритмы, позволяющие автоматизировать данный процесс. В данной статье рассматривается подход, предложенный исследователями Paul D. O’Grady и Scott T. Rickard в работе «Automatic ASCII Art Conversion of Binary Images Using Non-Negative Constraints». Описанный ими метод предполагает представление процесса преобразования изображения как задачи оптимизации и решение этой задачи при помощи неотрицательного матричного разложения. Ниже приведены описание рассматриваемого алгоритма, а также его реализация:

Описание алгоритма

Исходное изображение разбивается на блоки размером $M\times N$ , где

— ширина и высота одного символа в пикселях. Если ширина\высота изображения не кратна ширине\высоте символа, то картинка обрезается или дополняется белыми областями нужного размера.

Каждый из

блоков, полученных после разбиения, представляется в виде вектора длиной R=M*N

, значениями которого являются интенсивности цвета пикселей изображения (значения от 0 до 255, где белому пикселю соответствует значение 0, а черному — 255). Полученные векторы следует нормировать, используя норму l_2

$v_i= \frac{v_i}{\sqrt{\sum^R_{k=1}{v^2_k}}}$

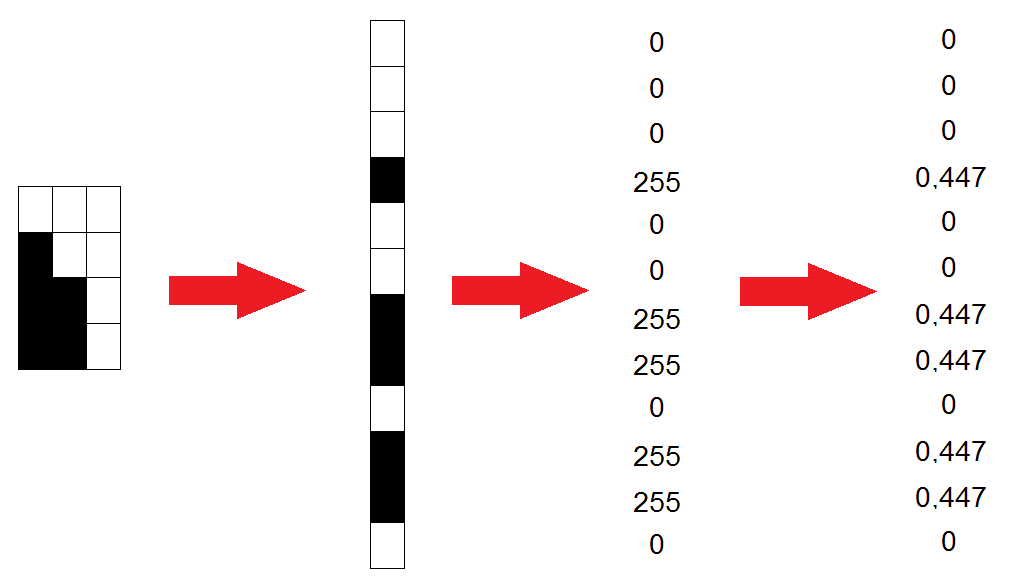
Нормированные векторы переписываются в виде столбцов, образуя таким образом матрицу

размером $R\times K$ .

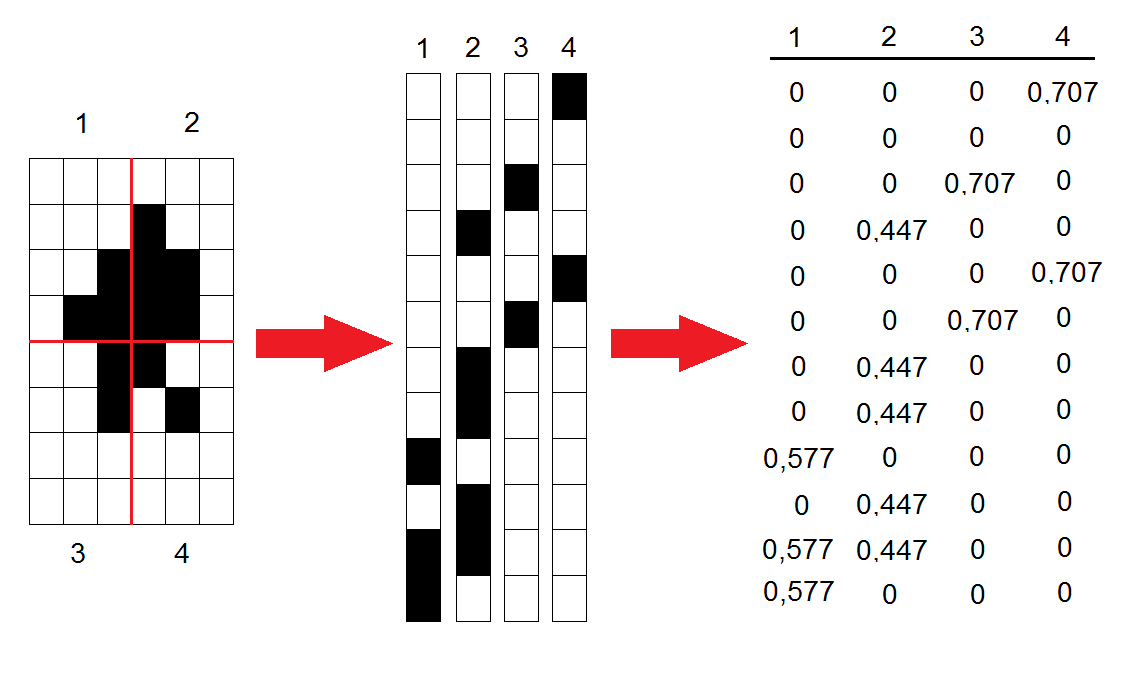
Полученную матрицу

нужно представить в виде произведения матриц

, все элементы которых неотрицательны:

$V_{R \times K}=W_{R\times L} H_{L \times K}$

Матрица

известна заранее: она строится аналогично матрице

, но вместо участков исходной картинки используются изображения всех символов, используемых при генерации ASCII-графики. Если применяемый набор включает в себя

символов, то матрица

будет иметь размер $R\times L$ .
Остается лишь подобрать матрицу

таким образом, чтобы минимизировать значение некоторой целевой функции, характеризующей разницу между

и произведением

. В качестве такой функции используется следующая зависимость:

$D(V,W,H,\beta)=\sum_{ik}\bigg({v_{ik}\frac{v_{ik}^{\beta-1}-[WH]^{\beta-1}_{ik}}{\beta(\beta-1)}}+[WH]^{\beta-1}_{ik}\frac{[WH]_{ik}-v_{ik}}{\beta}\bigg)$

Данное выражение по сути объединяет в себе несколько целевых функций: при $\beta = 2$ оно преобразуется в квадрат евклидова расстояния (Squared Euclidean Distance), при $\beta \rightarrow 1$ приближается к расстоянию Кульбака-Лейблера (Kullback-Leibler Divergence), а при $\beta \rightarrow 0$ — к расстоянию Итакуры-Сайто (Itakura-Saito Divergence).

Непосредственно подбор матрицы

производится следующим образом:

инициализируется случайными значениями от 0 до 1, после чего ее значения итеративно обновляются согласно следующему правилу (количество итераций задается заранее):

$h_{jk}=h_{jk}\frac{\sum^R_{i=1}{w_{ij}\frac{v_{ik}}{[WH]^{2-\beta}_{ik}}}}{\sum^R_{i=1}{w_{ij}[WH]^{\beta-1}_{ik}}}$

Каждое значение $h_{ij}$ соответствует степени схожести

-го символа из используемого набора с

-м участком изображения.

Таким образом, чтобы определить, каким символом следует заменить

-й участок, достаточно найти максимальное значение в

-м столбце матрицы

. Номер строки, в котором располагается данное значение, и будет номером искомого символа в наборе. Кроме того, можно ввести некоторое пороговое значение $\epsilon$ , и если найденное максимальное значение меньше этого порога, то участок изображения заменяется пробелом. Использование пробела может положительно сказаться на виде результирующего изображения по сравнению с использованием символа с низкой степенью схожести.

Реализация

Реализация алгоритма выполнена на языке C#. Для генерации ASCII-графики используются 95 символов (от 0x20 до 0x7E) размером 11x23 пикселей; применяемый шрифт — Courier. Ниже представлен исходный код функции преобразования исходного изображения в ASCII-графику:

public static char[,] ConvertImage(
    Bitmap image, 
    double beta,
    double threshold,
    ushort iterationsCount,
    ushort threadsNumber,
    Action<int> ProgressUpdated)
{
    int charNumHor = (int)Math.Round((double)image.Width / glyphWidth);
    int charNumVert = (int)Math.Round((double)image.Height / glyphHeight);
    int totalCharactersNumber = charNumVert * charNumHor;
    int glyphSetSize = wNorm.ColumnCount;

    Matrix<double> v = SplitImage(image, charNumVert, charNumHor);

    Matrix<double> h = Matrix<double>.Build.Random(
        glyphSetSize, 
        totalCharactersNumber, 
        new ContinuousUniform());

    int progress = 0;
    ushort step = (ushort)(iterationsCount / 10);

    for (ushort i = 0; i < iterationsCount; i++)
    {
        UpdateH(v, wNorm, h, beta, threadsNumber);

        if((i + 1) % step == 0)
        {
            progress += 10;

            if(progress < 100)
            {
                ProgressUpdated(progress);
            }
        }
    }

    var result = GetAsciiRepresentation(h, charNumVert, charNumHor, threshold);
    ProgressUpdated(100);

    return result;
}

Рассмотрим каждый ее шаг по отдельности:

1) Вычислим, какое количество символов можно уместить по ширине и по высоте изображения:

int charNumHor = (int)Math.Round((double)image.Width / glyphWidth);
int charNumVert = (int)Math.Round((double)image.Height / glyphHeight);

Используя рассчитанные значения, разобьем исходное изображение на блоки необходимого размера. Для каждого блока запишем значения интенсивности цвета пикселей в соответствующий столбец матрицы

(при необходимости расширим исходное изображение, добавив в матрицу нулевые значения, соответствующие белым пикселям), после чего нормализуем все столбцы:

private static Matrix<double> SplitImage(
    Bitmap image, 
    int charNumVert, 
    int charNumHor)
{
    Matrix<double> result = Matrix<double>.Build.Dense(
        glyphHeight * glyphWidth, 
        charNumHor * charNumVert);

    for (int y = 0; y < charNumVert; y++)
    {
        for (int x = 0; x < charNumHor; x++)
        {
            for (int j = 0; j < glyphHeight; j++)
            {
                for (int i = 0; i < glyphWidth; i++)
                {
                    byte color = 0;

                    if ((x * glyphWidth + i < image.Width) &&
                        (y * glyphHeight + j < image.Height))
                    {
                        color = (byte)(255 - image.GetPixel(
                            x * glyphWidth + i,
                            y * glyphHeight + j).R);
                    }

                    result[glyphWidth * j + i, charNumHor * y + x] = color;
                }
            }
        }
    }

    result = result.NormalizeColumns(2.0);

    return result;
}

2) Заполним матрицу

случайными значениями от 0 до 1:

Matrix<double> h = Matrix<double>.Build.Random(
    glyphSetSize, 
    totalCharactersNumber, 
    new ContinuousUniform());

Применим к ее элементам правило обновления заданное количество раз:

for (ushort i = 0; i < iterationsCount; i++)
{
    UpdateH(v, wNorm, h, beta, threadsNumber);

    if((i + 1) % step == 0)
    {
        progress += 10;

        if(progress < 100)
        {
            ProgressUpdated(progress);
        }
    }
}

Непосредственно обновление элементов матрицы реализовано следующим образом (к сожалению, проблемы, связанные с делением на ноль, решаются при помощи некоторых костылей):

private static void UpdateH(
    Matrix<double> v, 
    Matrix<double> w, 
    Matrix<double> h, 
    double beta,
    ushort threadsNumber)
{
    const double epsilon = 1e-6;
    Matrix<double> vApprox = w.Multiply(h);

    Parallel.For(
        0, 
        h.RowCount, 
        new ParallelOptions() { MaxDegreeOfParallelism = threadsNumber }, 
        j =>
        {
            for (int k = 0; k < h.ColumnCount; k++)
            {
                double numerator = 0.0;
                double denominator = 0.0;

                for (int i = 0; i < w.RowCount; i++)
                {
                    if (Math.Abs(vApprox[i, k]) > epsilon)
                    {
                        numerator += 
                            w[i, j] * v[i, k] / Math.Pow(vApprox[i, k], 2.0 - beta);
                        denominator += 
                            w[i, j] * Math.Pow(vApprox[i, k], beta - 1.0);
                    }
                    else
                    {
                        numerator += w[i, j] * v[i, k];

                        if (beta - 1.0 > 0.0)
                        {
                            denominator += 
                                w[i, j] * Math.Pow(vApprox[i, k], beta - 1.0);
                        }
                        else
                        {
                            denominator += w[i, j];
                        }
                    }
                }

                if (Math.Abs(denominator) > epsilon)
                {
                    h[j, k] = h[j, k] * numerator / denominator;
                }
                else
                {
                    h[j, k] = h[j, k] * numerator;
                }
            }
        });
}

3) Последний шаг состоит в выборе для каждого участка изображения подходящего символа путем нахождения максимальных значений в столбцах матрицы

private static char[,] GetAsciiRepresentation(
    Matrix<double> h, 
    int charNumVert, 
    int charNumHor, 
    double threshold)
{
    char[,] result = new char[charNumVert, charNumHor];

    for (int j = 0; j < h.ColumnCount; j++)
    {
        double max = 0.0;
        int maxIndex = 0;

        for (int i = 0; i < h.RowCount; i++)
        {
            if (max < h[i, j])
            {
                max = h[i, j];
                maxIndex = i;
            }
        }

        result[j / charNumHor, j % charNumHor] =
            (max >= threshold) ? (char)(firstGlyphCode + maxIndex) : ' ';
    }

    return result;
}

Полученное изображение записывается в html-файл. Полный исходный код программы можно найти тут.

Примеры сгенерированных изображений

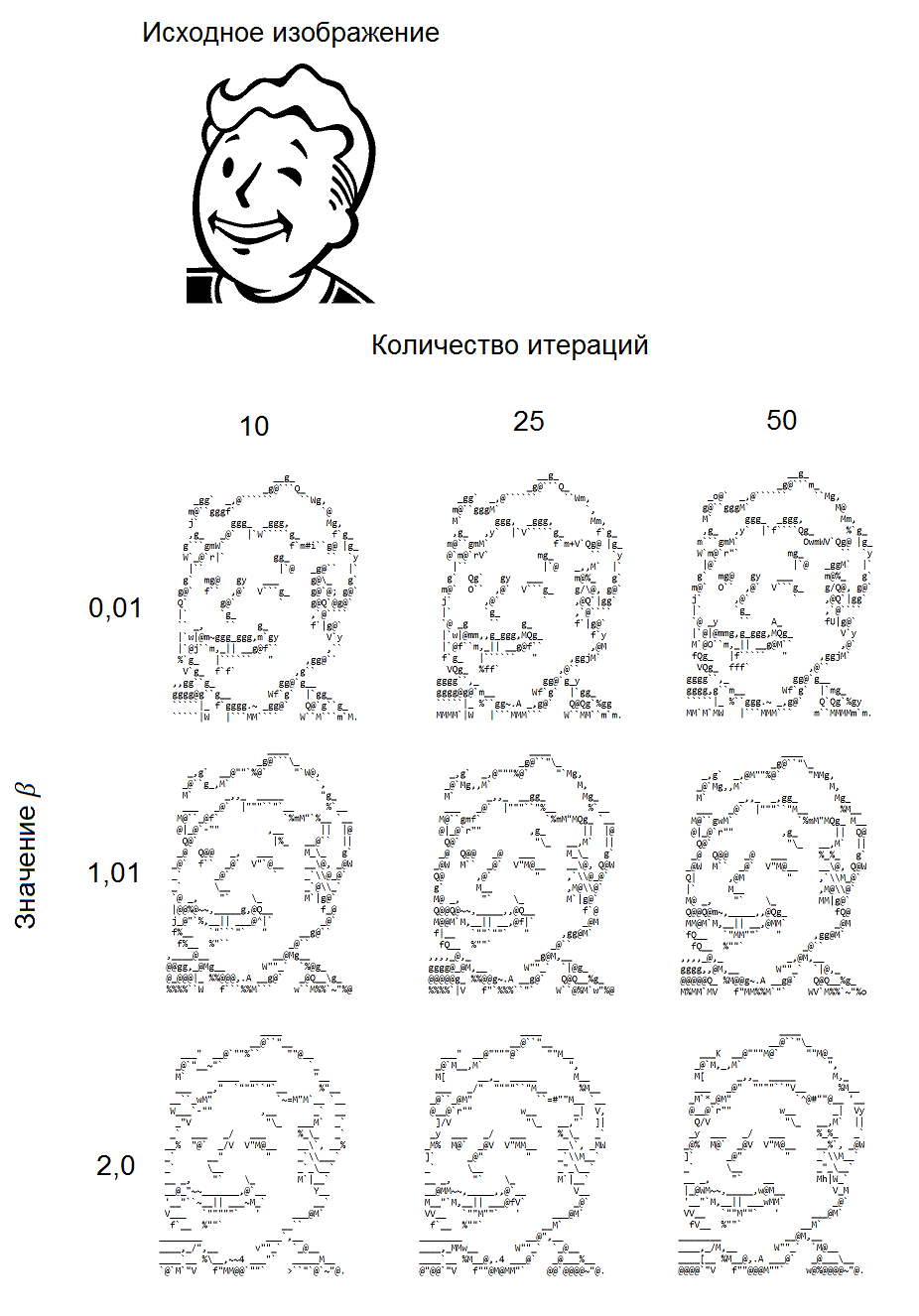
Ниже представлены примеры изображений, сгенерированных при различных значениях параметра $\beta$ и количествах итераций. Исходное изображение имело размер 407x500 пикселей, соответственно результирующие изображения имели размер 37x22 символов.

Заключение

В рассматриваемом алгоритме можно выделить следующие недостатки:

Долгая обработка изображений: в зависимости от размера картинки и количества итераций ее обработка может занимать от нескольких десятков секунд до нескольких десятков минут.
Низкое качество обработки детализированных изображений. Например, попытка преобразования изображения человеческого лица дает следующий результат:

В то же время уменьшение количества деталей за счет увеличения яркости и контрастности изображения позволяет значительно улучшить вид результирующего изображения:

В целом несмотря на перечисленные недостатки можно сделать вывод о том, что алгоритм дает удовлетворительные результаты.

Комментарии (19)

Chuvi
10.08.2019 22:12
#20491091
+1
inline, inline, везде инлайн. С формулами что-то не то.
1. Muttnik Автор
  10.08.2019 23:28
  #20491221
  Заменил все формулы на svg-картинки, надеюсь это решит проблему.

fingolfin
10.08.2019 22:21
#20491107
+1
Всегда привлекала ASCII-графика. В этом есть какая-то романтика, какая-то магия: ожидаешь увидеть в консоли сухой текст, и тут предстаёт красивая картинка!
1. click0
  11.08.2019 00:38
  #20491347
  Как тест моноширинного шрифта :)

corvair
11.08.2019 04:42
#20491465
Цвет ещё не помешал бы, для цветной матричной печати.

Static_electro
11.08.2019 08:53
#20491585
+3
Я когда-то игрался с таким, и обнаружил, что просто вычитание даёт достойный результат. Т.е. из блока изображения вычитал буковку, затем абсолютные значения всех пикселей разности складывал, и искал буковку, где результат наименьший.
У меня, к сожалению, нет под рукой тех картинок, но я не вижу качественного скачка в статье.
1. igormich88
  11.08.2019 15:17
  #20492227
  Наверное таким образом сделать и более умный перебор. То есть если символ совсем не подошел, отбрасывать все имеющие схожие элементы и наоборот если подошёл процентов на 50, пробовать символы имеющие похожие части. Но тут нужен хороший предварительный анализ всех символов

anandr
11.08.2019 14:32
#20492141
А если последнюю картинку с лицом инвертировать что получится?

DistortNeo
11.08.2019 14:48
#20492177
+1
Несмотря на матан, результирующие картинки выглядят, мягко говоря, не очень.
А причина простая: отсутствие хинтинга.
1. tyomitch
  11.08.2019 15:01
  #20492199
  +1
  Можете развернуть свою мысль для тех, кто не в теме?
  1. DistortNeo
    11.08.2019 16:24
    #20492315
    Так известный же термин — проще загуглить, что это такое.
    Плюс ещё идеи из пиксель-арта: лучше рисовать то, что приятно глазу, а не то, что максимально точно соотвествует оригиналу.
    https://habr.com/ru/post/241764/
    https://habr.com/ru/post/247333/
    
    tyomitch
    11.08.2019 16:38
    #20492339
    Не очень понятно, как термин из пиксель-арта применим к ascii.
    
    DistortNeo
    11.08.2019 20:18
    #20492807
    Потому что принципы рисования линий похожие.

gleb_l
11.08.2019 15:56
#20492279
Я делал проще: 1. Автоконтраст исходного, пока по чёрному/белому не будет по 3% гистограммы; 2. Усреднение Y в матрице 57, определение его попадания в 1 из 16 бинов; 3. Подстановка вместо блока 57 символа с визуальной плотностью, в среднем соответствующей бину. Таблицу плотностей символов рассчитал заранее и хранил в массиве

WST
11.08.2019 18:04
#20492517
+1
Когда-то давным-давно эту же задачу решал aa-project. Фишки своей библиотеки они продемонстрировали в очень крутой демке «bb», которую, правда, достаточно проблематично запустить со звуком в современных люнексах. А так нынче есть ещё libcaca. К слову, через обе библиотеки можно даже выводить видео, например, так:

mplayer -vo caca -framedrop -quiet tv:// mplayer -vo aa -framedrop -quiet tv://

Если у вас нет веб-камеры или она заклеена, вместо «tv://» подставьте какой-нибудь видеофайл. Особенно эффектно смотрится в голой консоли. Ну или можно просто запустить так:

DISPLAY="" mplayer -vo caca -framedrop -quiet tv://
Если вдруг кому лень пробовать…
1. WST
  12.08.2019 11:16
  #20494667
  Отвечу себе же, на YouTube есть видео данной демки.

asash
11.08.2019 23:58
#20493359
ИМХО вы перемудрили немного с матричным разложением. Набросал на коленке вариант в котором мы выбираем символ просто исходя из количества совпавших пикселей и средней яркости. Результат выглядит не хуже, хотя никакой линейной алгебры в данном случае не нужно
1. asash
  12.08.2019 00:03
  #20493363
  Собственно код который вычисляет похожесть участка изображения и пикселя в моем случае.
  
  def sim(pixels1, pixels2): b1 = pixels1.mean() b2 = pixels2.mean() return np.equal(pixels1, pixels2).mean() - abs(b1 - b2)
  
  В pixels1 — бирнаризованный участок изображения в виде еденичек/ноликов. в pixels-2 бинаризованное представление символа

berez

12.08.2019 00:58

#20493467

Не понимаю, к чему весь этот матан. ASCII art можно делать, используя два подхода:
— Статистический. Плотность краски имитируется разными символвами, а само изображение надо рассматривать издалека. Для этого подхода матан не нужен: берем пиксель, в зависимости от его плотности (черноты) выбираем символ из соответствующей таблички, выводим.
— А-ля пиксель-арт: тут каждый символ важен, т.к. именно форма символа «рисует» картинку. Сами картинки, как правило, небольшие и нарисованы вручную.

Вот простенький алгоритмик, по которому можно получить текстовую картинку первым способом:
— грузим картинку в память.
— ресайзим ее, слегка сплющивая по вертикали, до нужной ширины — например, 80 пикселей. Сплющивать надо, т.к. символы текста не квадратные, а прямоугольные.
— Переводим в черно-белое изображение и выводим на экран, заменяя пиксели на символы в зависимости от черноты (я использовал списочек «на глаз» — "#WMH@OTI*+;:-,. ").

Что получилось:

./ascii_art /mnt/seagate80/vault-boy.jpg
                                             .-,
                                           -@#MWWT,
                                         ,@#T,  :@W+
                      ..        .,:,,,,-*MW;      +W@:.
                   ,*HH,      :@#HO@M####H,        .*H#M@I:
                 .TWWW,     ,@WT,    ,*T+.            .;IH#H,
                ,M@,MW,   .+MT.                           :MH
                HM. :M#HO@WO-                              ,HI
               -#+    :+*;,                                 ,W:
               :#-             -+;.       -I@T-              :W*.
               ,#:          .*MOIOWT, .;TM#####I              ;MW+
                HT         ;MO-   .IMMWM@*;;*@##O.             .T#T
               T#W,      .OM;        ..       ,T#@.              I#I
              ;#@+H;.  -IWT.                    ;W@,.-;I@HM@I,    @#;
              @W, ,TWWMH*,                       :T@OT+;;;*H##+   ,WW.
              MM  .HW: -IH-                                 O##,   I#O
              TW..HM-.TT+:,                :O*              .##+   ,##,
              ,#IHW,                       ;O#O.            ,##:    H#+
               *#W-                          :HO           :MW;     O#*
               O#:     .                      .O:        *HWI.      @#*
              *#*    -MW-                      ..        IW*        W#:
             -#H     H##T       O+       ..             :I-T@,     -##.
             @#:    .W##+     .O@     ,@WW#WO-          .IW:;M-    T#H
            :#@      O#O     ,HM.      ,;OW##W-         ,.;M;:M,  .W#+
            O#;       .     ;WH,          .IW#I         +M+-M:+H  I#M.
           .WW.           .T#H,             ,O-          -HO-H,H:-##+
           :#@           ;M#O.                         .@;.@O;T*T@#@
           I#T           O##-                           :HT.H*OTW#W,
           T#*           .W#@                          :-.O*,W;W##;
           H#*            :##I                         -M+ * ;H##I
           H#*    ,.       ,-.        -,                :I  ,O##T
           @#O   *W.                  -M;                    O#W,
           T#H  O#WHT;,             -;T##@,                   M#@
           +##. ;#T.,;IOOOI*++ITOHH@O*;;@#W;                  I#W.
           -##+  O@TO:    ,-:::-,      -O##*                  H#H
            M#H  ., -OMI-         .:I@MI-TW.                 *##:
            *##;      ,IMWM@TTTT@MW@*-   I+                -@##;
             M#M.        -*T@@OI+-       .            +OTOM##O-
             :##O       ;I***:                      .T##@II;,
              I##*       ;OHH*                     -H#W+
               T##I                               IW#O.
                *##T.                           +M#W;
         ;IIITTTTH##M:                       .*M##OMH*,
         ;******+++H##T.                   :OW#M#T  -IMH*,
         I@HHHHHHI MM*@WT-                -I+:,@M.     ;##@;.
         O#######+;#:  ,*#H*,                ,@H,      +#*;HMI,
         O#######:IW     I###MT+:-..       -TWO.      .MW,+;-IW@:
         O#######-IW.     I####HOTI+,  .:IH#H:        O#I-##MI-*WH;
         O#######;+#:      -O###M@OOOHM##MT-         T#H,H####WI-*WH;
         *OOOOOOO*.O*        .;IOOOOOOI;,           +OT.;OOOOOOOT:.*O*.