В комментариях к опубликованным ранее работам автора было высказано много замечаний и пожеланий. Я благодарю всех читателей — хабровчан и прочих за внимание к работам и тем более за комментарии. Многих читателей не устраивал стиль изложения, подача материала, нечеткость определений и др. Главное, что автор желал бы поправить — это обеспечить доступность понимания идей публикаций, математического инструментария и техники его применения. Работа в интересующем автора направлении — дело и для него новое, но чем дальше «в лес», тем больше и непонятного, и сложного, и, конечно, интересного.


Введение.

В работах посвященных моделированию натурального ряда чисел (НРЧ) встречаются весьма любопытные и достаточно просто устроенные модели. Будем представлять точку как элемент, порождающий процесс создания или поиска элемента и назовем ее порождающей или поисковой точкой. Она движется по траектории поиска, задерживаясь в некоторых позициях (клетках), где производятся вычисления. Например, такими разыскиваемыми точками (позициями) являются центры ромбов, идентифицирующие числа-клетки в ромбах Г^2± – модели НРЧ. см.здесь и здесь

Поясним небольшим примером.

Пусть дана последовательность a, b, c, d, е, f, g, …. Тогда посредством последовательного процесса (как операции порождения) можно создать новую последовательность а, а + b, a + b + c, a + b + c + d, …. Результатом является последовательность частичных сумм ряда, порожденного последовательностью a, b, c, d, …. Таким образом, из постоянной последовательности 1, 1, 1, 1, … получается натуральный ряд чисел 1, 2, 3, 4, ….

Ограниченность доступных научных результатов и знаний в области моделирования Натурального ряда чисел и отдельного числа вынуждает автора заниматься встречающимися проблемами самостоятельно. Прекрасная традиция «Хабра» сопровождать публикации ссылками на аналогичные статьи и комментариями способствует поиску необходимых сведений, но тем не менее, движение вперед по ряду причин происходит медленнее чем хотелось бы.

Перечитал комментарии к прошлым статьям. Действительно, интерес имеется (52 комментария), но практически никто не понял, о чем работа. О новом ф-инварианте числа никто даже не упомянул. Наверное, в этом и моя недоработка, хотя я всегда ожидаю определенных усилий (пишу ведь не для развлечений) со стороны читателя, так как сам всегда напрягаюсь, читая о новом в науке.

Основные претензии читателей к понятиям НРЧ «контур», «полуконтур», «интервал» и другим с ними связанных. Думаю, все согласятся, что Спираль Улама – это плоская модель НРЧ. Клетки с числами закручиваются в спираль вокруг начальной клетки. Я предложил в начальную клетку поместить нуль, а дальше по спирали: над клеткой с нулем ставим 1 и движемся по клеткам против часовой стрелки. Начну с качественных пояснений основных понятий.

Первые восемь последовательных чисел в клетках (рис.1) 1, 2, 3, 4, 5, 6, 7, 8 оконтуривают по периметру клетку с нулем. Они лежат между клетками с последовательными нечетными квадратами 3 · 3 — 1 · 1 = 8 · k, k = 1, множество из 8-ми клеток от 1 до 9-й названы контуром с номером k = 1, далее следующие 16 клеток с числами 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24 оконтуривают по периметру первый контур и они лежат между квадратами следующих последовательных нечетных чисел 5 · 5 – 3 · 3 = 8 · k = 16; k = 2. Эти клетки с числами образуют контур с номером k = 2; так спираль можно продолжать до бесконечности.

Граничные клетки контуров содержат полные квадраты нечетных чисел, а в пределах контура среди его клеток, в одной из них содержится квадрат четного числа между нечетными в клетках границы контура. В первом контуре – 2 · 2 = 4, во 2-м 4 · 4 = 16, в 3-ем 6 · 6 = 36, в 4-ом 8 · 8 = 64 и так по всему НРЧ. Число клеток k-го контура обозначено L(k) и названо его длиной, она всегда кратна числу 8. Получить длину любого контура, номер которого задан, можно простым умножением восьмерки на номер контура 8k = L(k).

Четный квадрат k-го контура лежит не в произвольной клетке, а разделяет клетки контура на два неравных множества с нечетным числом клеток в каждом. Мощности множеств — последовательные нечетные числа. В первом контуре это три клетки с числами 1, 2, 3 и 5 клеток с числами 4, 5, 6, 7, 8; во втором контуре – это 7 клеток и 9 клеток; в 3-ем контуре – это 11 клеток и 13 клеток. Каждая из 2-х частей, при разбиении k-го контура обозначена m(k) и M(k) и названа полуконтуром. Клетка с четным квадратом (2k) · ( 2k) принадлежит большему множеству (полуконтуру M) и оно на 2 клетки превышает меньшее из двух.

Число клеток полуконтура – его длина, а сумма длин полуконтуров одного k-го контура равна длине этого контура L(k) = m(k) + M(k), где m, M – обозначения полуконтуров и их длины. Нечетные числа между квадратами последовательных чисел НРЧ (разной четности) – последовательные нечетные числа. Поскольку в НРЧ квадраты последовательных чисел размещаются в фиксированных позициях, а между ними количества клеток постоянны и равны последовательным нечетным числам, то такое представление НРЧ можно назвать его моделью. Из этой модели вытекает модель отдельного нечетного числа N = y · y — x · x.

Другими словами, любое нечетное число представимо разностью квадратов разной четности. Этот закон справедлив и для простых нечетных чисел. К сожалению, при этом необходимо
ограничиваться отождествлением нечетного числа с полуконтуром некоторого контура. Известно, что разность квадратов преобразуется в произведение, а именно,
N = y · y — x · x = (у — х)( у + х) = 1 · N, где х = ? (N — 1); и у = ? (N + 1), которое называется тривиальным разложением на сомножители. Это удобно, но этого мало.

Но оказывается можно выйти из этого порочного круга, если найти другую (альтернативную) пару квадратов удаление которых друг от друга окажется равным N. В этом случае квадраты сохраняют свойство иметь разную четность. Но мы знаем, что все квадраты нечетных чисел связаны с контурами, а четных чисел с полуконтурами. Ясно и то, что, располагая альтернативной парой квадратов для числа N, множество клеток, расположенное между клетками с этими квадратами, не имеет разрывов, т. е. каких-либо не учитываемых клеток.
Это как раз и означает, что множество клеток, моделирующее число N, представляет собой последовательность полуконтуров или последовательных нечетных чисел, где некоторые последовательные пары образуют контуры. Ясность в изложение помогает внести числовой пример.

Пример 1. Пусть задано число N = 105 = 3 · 5 · 7. Если рассматривать число 105 как длину одного полуконтура M(k) = 105, то квадраты разной четности
х · х и у·у легко вычисляются формулами х = ? (N -1) = 52; и у = ? (N + 1) = 53. Для N получается тривиальное разложение N = (53 — 52)(53 + 52) = 1·105. Квадраты являются границами полуконтура, большего в k-м контуре, так как 105 ? 1 (mod 4). Определим номер k и длину L(k) контура. Парный к полуконтуру M =105 полуконтур m(k) на 2 клетки (единицы) меньше, т.е. m(k) = 105 – 2 = 103, а их сумма (длина) контура L(k) = 103 + 105 = 208 = 8k, откуда номер контура k = 26. Номер полуконтура M(26) = 105 равен половине номера контура kп/2 = 26 / 2 = 13.

Укажем еще три пары квадратов (альтернативных), между каждой из которых лежит наше число N = 105: это 1-я пара 4 · 4 и 11 · 11; 2-я пара 8 · 8 и 13 · 13; 3-я пара 16·16 и 19 · 19. Убедимся, что это действительно альтернативные пары квадратов: 121 – 16 = 169 – 64 = 361 – 256 = 105.Рассмотрим последнюю из указанных пару квадратов. Она преобразуется в произведение N = 361 – 256 = (19 — 16)(19 +16) = 3 · 35 = 105 получили нетривиальное разложение на множители. Квадрат числа 16 это 256, за ним следуют квадраты чисел 17 · 17 = 289; 18 · 18 = 324 и, наконец, 19 · 19 = 361. Число клеток между квадратами разной четности: 289 — 256 = 33, между 324 — 289 = 35, и между 361 — 324 = 37.

Эти разности образуют фрагмент последовательности нечетных чисел 33, 35, 37 – или три полуконтура, так как в граничных клетках для каждого из них лежат квадраты разной четности. Какие два из трех чисел (полуконтуров) образуют контур? По определению контура его границы – в клетках, содержащих нечетные квадраты: 289 и 361. Сумма соответствующих клеток образует длину контура, которая должна быть кратна числу 8; 35 + 37 = 72 = 8k = 8 · 9, k = 9. Проверим другую пару 33 + 35 = 68, результат на 8 не делится. Других вариантов нет.

Сделаем вывод: число N = 105 представлено одним контуром, содержащим 72 клетки и одним полуконтуром из 33 клеток. Номер полного контура k = 9, а полуконтур принадлежит контуру с меньшим на 1 номером, следовательно, это больший (правый) полуконтур 33 ? 1 (mod 4) контура с номером k = 9 — 1 = 8. Контуры в НРЧ следуют один за другим по возрастанию длины и нумеруются по порядку. Номер меньшего полуконтура равен половине номера его контура, т. е. 8 / 2 = 4. Сумма номеров контура и полуконтура равна kп/2 = 8 / 2 + 9 = 13.

Теперь рассмотрим вторую пару квадратов 64 и 169. Между этими квадратами лежат квадраты 9 · 9, 10 · 10, 11 · 11, 12 · 12 и 13 · 13 завершает список. Между квадратами последовательных чисел лежат нечетные числа 81 — 64 = 17, 100 — 81 = 19, 121 – 100 = 21, 144 – 121 = 23, 169 – 144 = 25. Какие-то пары нечетных чисел–полуконтуров образуют контуры: 25 +23 = 48 = 8k = 8 · 6, k = 6; 21 + 19 = 40 = 8k = 8 · 5, k = 5; для 17 нет пары. Этот полуконтур принадлежит предшествующему контуру с номером k = 4, и его номер равен половине номера контура, 4 / 2 = 2. Имеем два полных контура 5-й и 6-й и большую половину контура с меньшим номером k = 4. Сумма номеров номеров контуров и полуконтура равна kп / 2 =4 / 2 + 5 + 6 = 2 + 5 + 6 = 13.

Осталась одна альтернативная пара квадратов 16 и 121. Между этими квадратами лежат 5 · 5, 6 · 6, 7 · 7, 8 · 8, 9 · 9, 10 · 10 и 11 · 11 завершает список. Между квадратами последовательных чисел лежат нечетные числа 25 -16 = 9, 36 – 25 = 11, 49 – 36 = 13, 64 – 49 = 15, 81 — 64 = 17, 100 — 81 = 19, 121 – 100 = 21. Какие-то пары нечетных чисел–полуконтуров образуют контуры: 21 + 19 = 40 = 8k = 8 · 5, k = 5; 17 + 15 = 32 = 8k = 8 · 4, k = 4; 13 + 11 = 24 = 8k = 8 · 3, k = 3; для 9 нет пары. Этот полуконтур принадлежит предшествующему контуру с номером k = 2, и его номер равен половине номера контура, 2 / 2 =1. Имеем три полных контура 3, 4, 5 и большую половину контура с меньшим номером k = 3 — 1 = 2. Сумма номеров контуров и полуконтура равна kп/2 = 2 /2 + 3 + 4 +5 = 13.

Пары альтернативных квадратов для составного нечетного натурального числа N = 105 приводят к разным ситуациям, в которых много общего. Между квадратами в граничных клетках одинаковое число клеток 105, которое будем называть интервалом. Эти интервалы разбиваются промежуточными квадратами по-разному, что порождает разное число различных нечетных чисел (слагаемых), а именно, 3, 5 и 7. Это число слагаемых в суммах из 105 клеток. В каждой ситуации число слагаемых нечетное. Значит среди них имеется среднее слагаемое – это числа 35, 21 и 15. Произведение среднего слагаемого на количество слагаемых дает одинаковый результат 3 · 35 = 5 · 21 = 7 · 15 = 105. Относительно слагаемых заметим, что это последовательные нечетные числа и каждое из них в НРЧ ограничено слева и справа квадратами разной четности.

Интервал отличается от контура тем, что содержит не менее трех полуконтуров (в контуре их только два); ограничивается квадратами разной четности (для контура оба граничных квадрата нечетные); и длина интервала (число клеток в нем) не обязана быть кратной числу 8 как в контуре. Интервалы для составных чисел могут возникать в разных областях НРЧ, как нечетные числа, образуемые из суммы последовательных нечетных чисел. Из нашего примера видим, что интервалы могут даже пересекаться, т.е. иметь одинаковые слагаемые в образующих их длину суммах.

Теперь обратим внимание на то, что во всех 4-х рассмотренных ситуациях подсчитывалась сумма номеров контуров, которая оказывалась для N = 105 постоянной и равной числу 13, т.е. половине номера контура k = 26. Этот номер для произвольного N легко вычисляется, и его половина называется ф-инвариантом числа N. Оказывается, альтернативные пары квадратов можно находить, если определены номера контуров, образующих число N.

В свою очередь эта задача (определение номеров образующих число N контуров) решается путем получения специальных комбинаторных разбиений числа (для примера) kп / 2 =13 на части (слагаемые), отличающиеся от предыдущих на единицу: 5 + 4 + 3 + 2 / 2 = 6 + 5 + 4 / 2 = 9 + 8 / 2 = 13. Таким образом, задача факторизации числа N может быть сведена к комбинаторной задаче о специальных разбиениях чисел.

Контурная модель НРЧ.

В предлагаемом подходе к моделированию натурального ряда чисел, этот ряд и его элементы получает другую не совсем обычную интерпретацию. Представим НРЧ как бесконечное множество пронумерованных ячеек, образующих линейный регистр, в каждую из которых подряд, начиная с первой, вписано число из натурального ряда чисел равное ее номеру.

Слева к регистру можно добавить ячейку с нулевым значением, которое отсутствует в НРЧ. Структура числовых квадратов на числовой оси закрепляется в их позициях (ячейках) и не меняется при вычислениях, а для всех других чисел на оси в модели учитываются только их позиции, а не значения. Множества этих позиций представляют собой промежутки между закрепленными на числовой оси НРЧ квадратами, а мощности множеств соответствуют рассматриваемым и обрабатываемым числам N.

Основная роль в контурной модели отводится нечетным числам (Осн.теорема факторизации). В терминах контурной модели всегда все нечетные числа представляются непрерывной последовательностью позиций (контентом), формируемой из целых полуконтуров (определения даются ниже).

В крайних позициях полуконтуров и соответственно контуров, и интервалов при этом всегда размещаются квадраты чисел и тогда N = y² — x², где Г_л(N) = х² = [(N — 1)/2]² и Г_п(N) = у² = [(N + 1) / 2]². Пара чисел (х, у) не единственная, между квадратами которых лежит заданное число N. Определить другие (альтернативные) пары очень непросто, но для составных N они существуют. Именно они обеспечивают быструю факторизацию числа.

Преимущества такого рассмотрения чисел и НРЧ состоит в том, что границы левая и правая (Г_i) промежутков (интервалов), соответствующих произвольным нечетным числам, всегда полные квадраты, а значение нечетного числа N равно разности Г_п(N) правой (большей) и Г_л(N) левой (меньшей) границ промежутков N = Г_п(N) — Г_л(N).

Таким образом, на фоне структуры закрепленных в НРЧ числовых квадратов нечетные числа рассматриваются не точками, а последовательностями ячеек (точечных позиций), размещаемых между ячейками с закрепленными в НРЧ квадратами последовательных натуральных чисел, т. е. чисел переменной (чередующейся) четности. Особенностью такого представления нечетных чисел N в контурной модели является то, что все контуры, полуконтуры, интервалы для N — это промежутки, образованные ячейками регистра и в крайних ячейках промежутков всегда лежат квадраты натуральных чисел.

Такое положение обеспечивает представление любого N разностью границ представляющего число N промежутка (интервала), т. е. разностью квадратов, которая в свою очередь легко преобразуется в произведение чисел, обеспечивая факторизацию числа N.


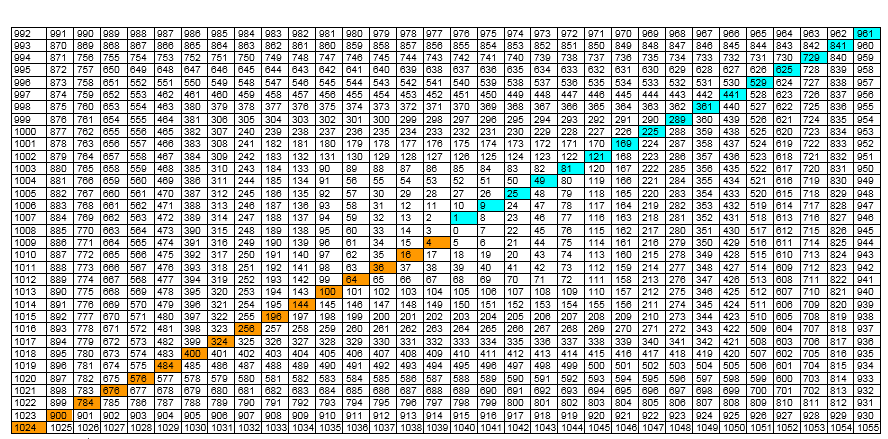
Рисунок 1 Регистр с НРЧ закрученный вокруг клетки с нулем подобно спирали Улама

Каждое нечетное число, и такие объекты как множество непрерывных позиций чисел, образующих контуры, полуконтуры и интервалы, жестко привязаны к их положению (позиции) в НРЧ. Структура этой модели постоянная, положение ее элементов в НРЧ не меняется.

Имеется теорема о представимости любого нечетного числа N разностью двух квадратов чисел разной четности. В случае, когда числа смежные, они легко устанавливаются как границы полуконтура N через номер контура.

Положение любого нечетного числа N в НРЧ, представляемого как разность квадратов двух смежных чисел разной четности и измеряемого количеством позиций (ячеек) между позициями (ячейками) с квадратами, определено его границами — квадратами смежных чисел, имеющих разную четность, зависящими от N и определяемыми формулами:

Г_л(N) = х² = [(N — 1) / 2]² и Г_п(N) = у² = [(N + 1) / 2]².

Это справедливо для положения числа N в предельном контуре. Такая привязка нечетного числа N к НРЧ используется при вычислениях. Границы (ячейки начала и конца объектов) контуров, полуконтуров и интервалов — всегда квадраты чисел, для которых четность и положение (начало, конец) в НРЧ определяется однозначно. Если число N простое, то представление его разностью квадратов N = y² — x² единственно; для составных чисел N, кроме такого представления существуют и другие представления интервалами, у которых в граничных ячейках размещаются другие пары квадратов.

Для удобства манипулирования с числами N вводится разделение нечетных натуральных чисел на два класса (класс левых и класс правых в зависимости от положения в предельном контуре), а более формально в зависимости от объективного их свойства сравнимости по модулю 4:

• для левых нечетных чисел выполняется сравнение N ? 3( mod4) и
• для правых нечетных чисел — сравнение N ? 1( mod4).

Теперь введем несколько понятий и определений, которые потребуются в дальнейшем.

Контуры и их границы образуют структуру (скелет) модели НРЧ.

Выберем пару (х, у) последовательных (смежных) нечетных чисел х = (2k — 1), у = (2k + 1); у > x в соответствующих ячейках НРЧ, где k — произвольное натуральное число. Между этими ячейками (с числами) имеется единственная ячейка с четным числом z = (2k).

Возведем числа х, у, z в квадрат. Квадрат х² = (2k -1)², квадрат у² = (2k +1)², квадрат z² = (2k)². Относительное положение ячеек с квадратами чисел останется таким же как и прежде (для первых степеней чисел) но ячейки с квадратами будут уже более удалены друг от друга. Ячейка с четным квадратом будет лежать между ячейками с нечетными квадратами, определяющими один k-й контур. Между ячейками с квадратами чисел появятся ячейки с новым содержанием.

Модуль разности чисел (квадратов чисел) в крайних ячейках объектов назовем расстоянием между ячейками их содержащими, и обозначим символом L(k) = y² — х² = (2k+1)² — (2k-1)² = 8k, которое будем измерять числом ячеек между y² и х². Такое определение расстояния удовлетворяет всем аксиомам расстояния.

Известно, что любое нечетное число представимо разностью квадратов разной четности:

• так — для правых нечетных чисел N_п(k) = (2k+1)² — (2k)² или
• так — для левых нечетных чисел N_л(k) = (2k)² — (2k — 1)².

Более того, для составного нечетного натурального числа (СННЧ) такое представление не единственно.

Именно квадраты НРЧ формируют структуру его контурной модели.
Среди ячеек НРЧ встречаются ячейки, содержащие квадраты натуральных чисел с чередующейся четностью 1², 2², 3², 4²,…

Между ячейками, содержащими квадраты последовательных нечетных чисел 1², 3², 5², 7², 9², 11², 13², 15², ...и так до ?, всегда располагаются промежутки из ячеек, количество которых кратно числу 8.

Действительно, 3² — 1² = 1 • 8, 5² — 3² = 16 = 2 • 8, 7² — 5² = 24 = 3 • 8, 9² — 7² = 32 = 4 • 8, ...,
(2k + 1)² — (2k — 1)² = 8k ,...и так до ?. Промежутки длиной L(k), образованные этими ячейками (L(k) количество ячеек в промежутке между квадратами последовательных нечетных чисел), будем называть контурами. Все контуры получают порядковые номера k, пробегающие значения от 1 через 1 и до бесконечности, что нам удобно будет обозначать так
k = 1(1)?.

Удобство символа k = 1(1)? состоит в том, что в скобках можно указывать другие значения шага перечисления, например, для задания последовательности положительных нечетных чисел пишем
НЧ = 1(2)?, что соответствует 1,3,5,7,...; а для задания последовательности четных чисел пишем ЧЧ = 0(2)?, что соответствует 0,2,4,6,.... Номера всех контуров определяются выражением k = L(k)/8. Отсюда длина контура определяется через его номер формулой L(k) = 8k. Крайняя левая ячейка каждого контура всегда содержит квадрат нечетного числа и ее положение в НРЧ соответствует точке НРЧ с этим числом.

Каждый контур НРЧ характеризуется именем, номером k, значениями границ: левой
Г_л(N) =(2k — 1)² и правой Г_п(N) =(2k + 1)², длиной (числом позиций-ячеек)
L(k) = 8k = Г_п(N) — Г_л(N) = (2k + 1)² — (2k — 1)².

Контур — множество ячеек регистра с числами между ячейками с квадратами последовательных (смежных) нечетных чисел. Мощность множества ячеек k-го контура обозначим символом L(k) = y² — х² = (2k+1)² — (2k-1)² = 8k и назовем длиной контура. Длина контура определяется разностью квадратов последовательных нечетных чисел, его границ, и равна восьмикратному значению натурального числа k.

Таким образом, k-й контур образован ячейками и имеет начальную ячейку, содержащую квадрат меньшего ( х ) из двух нечетных чисел, называемую в модели НРЧ левой границей Г_л(k) = (2k — 1)² контура, и конечную ячейку, называемую правой границей Г_п(k) = (2k + 1)² контура. В одной из промежуточных ячеек k-го контура содержится квадрат z² = (2k)² четного числа, называемый средней (центральной) границей Г_ц(k) = (2k)² контура.

Весь НРЧ разбивается квадратами нечетных натуральных чисел на промежутки, представляющие собой последовательные контуры, длины которых можно рассматривать как элементы арифметической прогрессии с начальным элементом а = 8 и разностью d = 8, причем так, что номера контуров следуют подряд один за другим, как и сами контуры без перекрытий, и образуют сам НРЧ. Длины двух последовательных контуров с номерами k и k+1 различаются на 8 единиц, а длина каждого контура в отдельности с номером k пропорциональна числу 8, т.е. L(k) = 8k.
Поясним контурную структуру НРЧ числовыми примерами.

Пример 2. Рассмотрим пару смежных контуров 9-й и 10-й с номерами k = 9 и k =10.
Определим длину каждого контура как функцию номера контура L(9) = 9 • 8 = 72 и L(10) = 10 • 8 = 80. Разность длин смежных контуров L(10) — L(9) = 80 — 72 = 8 составляет 8 единиц.

Найдем границы контуров и через них вычислим их длину:
Девятый контур: левая граница Г_л(k) =(2k — 1)² = (2 • 9 — 1)² = 289 и правая граница Г_п(k) =(2k + 1)² =(2•9 + 1)² = 361.

Десятый контур: левая граница Г_л(k) =(2k — 1)² = (2•10 — 1)² = 361 и правая граница Г_п(k) = (2 • k + 1)² = (2 • 10 + 1)² = 441.

Вычисляем длины контуров как разность их границ:

L(9) = Г_п(9) — Г_л(9) = 361 — 289 = 72;
L(10) = Г_п (10) — Г_л(10) = 441 — 361 = 80.

Заметим, что у контура с меньшим номером правая граница (361) совпадает с левой границей большего.

Среди ячеек каждого k-го контура имеется ячейка с квадратом четного числа (2k)². Четный квадрат (2k)² во внутренней ячейке (контура с номером k) разбивает множество ячеек контура на два подмножества (полуконтура, блока): слева от (2k)² и справа от (2k)², которые обозначаются как m(k) — левый полуконтур и M(k) — правый полуконтур.

Эта ячейка делит множество ячеек контура на две части левую с длиной L(m(k)) = 4k-1 и правую с длиной L(M(k)) = 4k +1. Количество ячеек, попадающее в левый полуконтур (слева от ячейки с четным квадратом), всегда на две меньше чем в правом полуконтуре L(M(k))- L(m(k)) = 2. Длины полуконтуров это всегда два смежных нечетных числа. Суммарная длина полуконтуров L(M(k))+ L(m(k)) =L(k) равна длине k-го контура.

Границы полуконтуров в k-ом контуре правая граница левого полуконтура и левая граница правого полуконтура совпадают и равны четному квадрату в контуре. Эта граница обозначается как центральная граница k-го контура Г_ц(k) = (2k)². Внешние границы обоих полуконтуров левая левого полуконтура Г_л(k) = (2k — 1)² и правая правого полуконтура
Г_п(k) = (2k + 1)² совпадают с соответствующими границами самого k -го контура.

Полуконтур — множество ячеек регистра между ячейками с квадратами последовательных (смежных) чисел НРЧ, имеющих разную четность. Каждый полуконтур имеет границы в крайних клетках своего множества ячеек. Имеем описание границ полуконтуров:
— для левого полуконтура левой границей является левая граница контура Г_л (m(k)) = Г_л (k), а правой границей — центральная граница контура Г_п (m(k)) = Г_ц (k); — для правого полуконтура левой границей является центральная граница Г_л (M(k)) = Г_ц (k) контура, а правой границей — правая граница контура Г_п (M(k)) = Г_п (k). Видим, что полуконтуры каждого контура лежат между квадратами разной четности, следовательно, они являются нечетными числами и, более того, последовательными нечетными числами с разностью в две единицы.

Весь НРЧ разбивается квадратами натуральных чисел на промежутки, представляющие собой (нечетные числа) последовательные полуконтуры, длины которых можно рассматривать элементами еще одной возрастающей арифметической прогрессии с начальным элементом а = 3 (наименьший полуконтур в НРЧ) и разностью d =2.

С другой стороны, не любые два последовательных нечетных числа (ячейки) при их конкатенации в ячейках регистра образуют контур. Одно из свойств контура — делимость его длины на 8. Так числа 11 и 13 образуют контур 11 +13 = 24 = 3•8 с номером k = 3, а числа 13 и 15 контур не образуют, сумма 13 + 15 = 28 ? 0(mod8) не кратна восьми.

Для последней суммы нарушено и другое свойство контура — его границы должны быть квадратами только нечетных чисел. Для числа 13 (правый полуконтур из третьего контура) имеем: левая граница Г_л(M(k =3)) = Г_ц(k = 3) = (2•3)²= 36 — число четное и эта граница не может быть крайней границей контура.

Пример 3. Располагая значениями границ полуконтуров k-го контура, возможно определить длину полуконтура, как разность его границ:
левый полуконтур k-го контура имеет длину L(m(k)) = Г_п (m(k)) — Г_л (m(k)) = Г_ц (k) — Г_л (k) = (2k)² — (2k — 1)² = 4k — 1. Правый полуконтур k-го контура имеет длину
L(M(k)) = Г_п (M(k)) — Г_л (M(k)) = Г_п (k) — Г_ц (k) = (2k + 1)² — (2k)² = 4k + 1.

Поскольку левый и правый полуконтуры образуют k-й контур, то сумма их длин равна длине k-го контура L(k) = L(m(k)) + L(M(k)) = 4k — 1 + 4k +1 = 8k.
Эти характеристики иллюстрируются рисунком 2, на котором n = k. Полуконтуры не получают собственных номеров (хотя это легко ввести), для их характеризации используется половина номера, того контура, которому они принадлежат.


Рисунок 2 — Представление контура с номером k = n и его полуконтуров на числовой оси

Выражения 4k — 1, 4k + 1 описывают длину левого и правого полуконтуров, а выражения (2k — 1)², (2k)², (2k + 1)² описывают границы левую, среднюю и правую этого контура.

Пример 4. Выполним расчеты характеристик полуконтуров для исходных данных примера 3.

Длина полуконтуров через номер контура k:

k = 9.
левый полуконтур L(m(k)) = 4k — 1 = 4 • 9 — 1 = 35 и правый полуконтур L(M(k)) = 4k +1 = 4 • 9 + 1 = 37, разность длин полуконтуров 37 — 35 = 2.

k = 10.
левый полуконтур L(m(k)) = 4 • k — 1 = 4 • 10 — 1 = 39 и правый полуконтур L(M(k)) = 4k +1 =4 • 10 + 1 = 41, разность длин полуконтуров 41 — 39 = 2.

Длина полуконтуров через вычисление их границ. Определим границы полуконтуров и через них вычислим их длину:

для m(9): левая граница Гл(k) = (2k — 1)² = (2 • 9 — 1)² = 289 и правая граница Гп(k) = Гц(k) =(2k)² = (2 • 9)² = 324, M(9): левая граница Гл(k) = Гц(k) = (2k)² = (2 • 9)² = 324 и правая граница Гп(k) = (2k + 1)² = (2 • 9 + 1)² = 361,

для m(10): левая граница Гл(k) = (2k — 1)² = (2 • 10 -1)² = 361 и правая граница Гп(k) = Гц(k) = (2k + 1)² = (2 • 10)² = 400, M(10): левая граница Гл(k) = Гц(k) = (2k)² = (2 • 10)² = 400 и правая граница Гп(k) = (2k + 1)² =(2 • 10 + 1)² = 441.

Вычисляем длины полуконтуров через найденные границы:

для k = 9: L(m(9)) = Гц(9) — Гл(9) = 324 — 289 = 35; L(M(9)) = Гп(9) — Гц(9) = 361 — 324 = 37.

для k = 10: L(m(10)) = Гц(10)-Гл(10) = 400 — 361 = 39; L(M(10)) = Гп(10) — Гц(10) = 441 — 400 = 41.

Длины контуров как суммы длин полуконтуров:
для k = 9: L(k) = L(M(k)) + L(m(k)) = L(9) =37 + 35 = 72;
для k = 10: L(k) = L(M(k)) + L(m(k)) = L(10) = 41 + 39 = 80.

Каждое нечетное число N, рассматриваемое как полуконтур, принадлежит единственному контуру, называемому предельным контуром.

Пример 5. Выполним расчеты характеристик двух нечетных чисел N = 983 и N = 987. Первое число нечетное простое. Оно представлено в НРЧ полуконтуром, т. е. множеством позиций-ячеек. Вначале установим принадлежность N к левому или к правому классу нечетных чисел; 983 ? 3( mod4), число N=983 левое. В своем контуре оно находится слева от центральной границы. Смежное справа нечетное число равно 985 и их сумма равна длине контура L(k) = 983 + 985 = 1968 c номером k =1968/8 = 246.

Итак, имеем m(k = 246) = 4k — 1 = 983.

Этот полуконтур имеет границами квадраты смежных чисел: Гл(m(246)) = (2k — 1)² = 491² = 241081 и
Гп(m(246)) = Гц (m(246)) = (2k )² = 492² = 242064.

Простое число N = 983 лежит между границами-квадратами смежных чисел и может быть разложено на множители (факторизовано).

N = 983 = Гц — Гл = 242064 — 241081 = (492 — 491)(492 + 491) =1 • 983. Получили тривиальное разложение на множители.

Приступим к обработке составного числа N = 987. Число 987 ? 3( mod4) лежит в классе левых чисел и принадлежит контуру с номером k = (987 + 989) / 8 = 247. Этот контур является смежным с контуром для числа 983 (предшествующим), его длина на 8 единиц больше предыдущего. Структура смежных контуров НРЧ определяется их границами: 491²/ 492²/ 493²/ 494²/ 495². Общей для обоих контуров является граница 493².

Для числа N = 987 определим номер его предельного контура k = (987 + 989) / 8 = 247, границы контура квадраты смежных нечетных чисел:
Гл(m(247)) = (2k — 1)² = 493² = 243049 и
Гц(m(247)) = (2k )² = 494² = 244036 и
Гп(m(247)) = (2k + 1)² = 495² = 245025,

разложение на множители его левого полуконтура:
N = 987 = Гц — Гл = Гц(m(247)) = (2k )² — Гл(m(247)) = (2k — 1)² = (494 — 493)(494 + 493) =1 • 987
получили тривиальное разложение, так как рассматривался предельный контур, в котором число N = 987 — полуконтур.

Но так как число N = 987 составное, то на основе анализа контурной структуры числа можно указать альтернативную пару квадратов, в интервале между которыми лежит это число и интервал содержит более одного полуконтура.
Число N = 987 = 327 + 329 + 331 представимо суммой трех смежных нечетных чисел, образующих интервал из 987 позиций. Каждое из этих чисел является полуконтуром в своих предельных контурах.
Определим номера контуров: k = (327 +329) / 8 = 656 / 6 = 82, следующий контур как смежный должен иметь номер на единицу больше k = 83.

Теперь можно определить границы всех полуконтуров, но нам потребуются только две границы — крайние для интервала длиной 987:
Гл(987) = Гл(m(82)) = (2k — 1)² = 163² = 26569 и
Гп(987) = Гц(m(83)) = (2k )² = 166² = 27556.
Разность этих границ-квадратов интервала равна числу N = 987 и обеспечивает его нетривиальную факторизацию

N = 987 =(166 -163)(166 + 163) = 3 • 329.
Делитель d = 329 числа N = 987 — составное число и может быть подвергнут дальнейшей аналогичной обработке для завершения факторизации числа N = 987 =3 • 329 = 3 • 7 • 47.

Интервалы и их границы образуют основу модели отдельного натурального числа
Основное отличие интервалов от контуров и полуконтуров в том, что положение контура и, следовательно, его полуконтуров в НРЧ постоянное (закрепленное), а интервал может формироваться из таких закрепленных промежутков в разных частях НРЧ. Контур — это интервал из двух полуконтуров, сумма которых кратна числу 8. Границы контура всегда квадраты смежных нечетных чисел. Важно понимать, что любое СННЧ N образуется нечетным количеством последовательных нечетных чисел, т.е. полуконтуров, сумма длин которых как раз и равна значению N.

Поскольку любое СННЧ N можно представить разностью квадратов чисел разной четности, то предположим, что ему (числу N) соответствуют в разных местах НРЧ множества из N ячеек регистра (интервалы) с квадратами чисел в крайних ячейках. Эти N ячеек группируются из полуконтуров и контуров по-разному, что и показано границами (числами-квадратами) рис. 3).

Интервал — множество ячеек регистра между крайними ячейками, содержащими квадраты не смежных чисел НРЧ, имеющих разную четность. Интервалы (более одного), представляющие одно СННЧ N, могут перекрываться (рис.3), что исключено для контуров и полуконтуров. В этом множестве между парами крайних ячеек (границами интервала) могут содержаться квадраты чисел разной четности (фрагменты контурной структуры).

Множество ячеек интервала всегда разбивается на целое число полуконтуров, количество которых должно быть нечетным и равным меньшему делителю N, так как длина любого полуконтура — нечетное число. Средний полуконтур из числа формирующих интервал, равен большему делителю N. Крайние ячейки множества с квадратами из определения играют роль границ интервала и могут отстоять одна от другой как угодно далеко.

Между граничными ячейками интервала может встречаться множество ячеек с другими квадратами, не превышающими значения правой границы интервала. Ранее было показано, что все квадраты НРЧ являются граничными значениями объектов (у контура оба квадрата нечетные, у полуконтуров четность квадратов на границах разная). Отсюда следует, что аддитивное строение интервала, соответствующего составному нечетному числу всегда может быть представлено последовательностью множества полуконтуров.

Пример 6. Задано число N = 105 = 7 • 15. N = 105 ? 1 (mod 4) — правое нечетное число. Его можно представить с одной стороны, разностью квадратов разной четности,
например 121 — 16 = 105, с другой стороны, интервалом составленным из 7 последовательных полуконтуров (из 7-ми нечетных чисел) со средним полуконтуром с длиной равной 15, т.е. 105 = 9 + 11 + 13 + 15 + 17 + 19 + 21 суммарной длиной равной 105. Все семь полуконтуров в НРЧ имеют границами полные квадраты, следовательно, и представляющий интервал в качестве своих границ имеет те же самые крайние ячейки (левую и правую) крайних полуконтуров (с длиной 9 и 21).

Четный квадрат — левая граница интервала (левая граница полуконтура с длиной 9) должен совпадать с четной (центральной) границей полуконтура. Этот полуконтур должен быть крайним (левым) в интервале. Однозначно это определяется после установления принадлежности N одному из двух классов (левое, правое число N) нечетных чисел.
Для левого СННЧ полуконтур должен быть крайним справа, для правого СННЧ — крайним слева. Остальные полуконтуры естественным образом попарно объединяются в контуры, номера которых образуют фрагмент НРЧ, т.е. номера смежных контуров различаются только на единицу.

Пример 7. На рисунке 3 на числовой оси изображены четыре интервала НРЧ, представляющих СННЧ N = 105. На числовой оси указаны границы каждого из четырех интервалов (это пары квадратов разной четности), а длины интервалов показаны фигурной скобкой с указанием значения длины — она одинакова (= 105) для всех интервалов.

Границы самого правого интервала являются парой квадратов смежных чисел. Это означает, что этот интервал не подпадает под определение интервала и является исключением. Заданное число N = 105 ? 1(mod 4) в НРЧ представляется правым полуконтуром предельного контура и вместе с левым полуконтуром, его длина по отношению к правому полуконтуру на 2 единицы меньше, они образуют предельный контур. Это контур с длиной 103 + 105 = 208 и с номером k = 208 / 8 = 26. Границы этого контура и полуконтура устанавливаются через найденный номер 26.

Само число N=105 характеризуется половиной номера контура, т.е. k(105) / 2 =26 / 2 = 13.
Для контура с номером k = 26 имеем:
— левая граница Г_л(k) = (2k — 1)² = (2 • 26 — 1)² = 51²;
— правая граница Г_п(k) = (2k +1)² = (2 • 26 + 1)² = 53²;
— средняя граница Г_ц(k) = (2k)² = (2 • 26)² = 52².
и правый полуконтур лежит между квадратами 53² и 52²


Рисунок 3 — Представление 4-x интервалов для правого полуконтура N = 105 из контура с номером k = 26;
Для каждого интервала СННЧ N =105 указано его положение в НРЧ парой границ — квадратов (4² и 11²); (8² и 13²);(16² и 19²); (52² и 53²).

Так как N = 105 правое число, то во всех представляющих интервалах левый крайний полуконтур имеет левой границей четное число. Рассмотрим на рис. 3 левый интервал с границами 4² и 11². Решим обратную задачу: имеется левая граница полуконтура (четный квадрат 4²) определить значение длины полуконтура.
Имеем для средней границы Г_ц(k) = (2k)² = (2•2)² = 4², т.е. k = 2 и длина правого полуконтура L(M(2)) = 4k + 1 = 4 • 2 + 1= 9.

Следующим за контуром с k = 2, от которого в интервал включается лишь полуконтур с L(M(2)) = 9, будет контур с k = 3 (его длина L(3) = 3 • 8 = 24), за ним с k = 4 (его длина L(4) = 4 • 8 = 32), затем k =5 (L(5) = 40). Вычислим суммарную длину полуконтура и 4-х контуров, т.е. длину интервала L(105) = 9 + 24 + 32 + 40 = 105 и сумму номеров контуров
2/2 + 3 + 4 + 5 =13.

Выполним такие же действия для следующего представляющего число N интервала с границами 8² и 13². Левая граница полуконтура (четный квадрат 8² ) совпадает с левой границей интервала. Определим значение длины полуконтура. Имеем для этой границы Г_л(k) = (2k)² = (2•4)² = 8², т.е. k = 4 и длина полуконтура L(M(4)) = 4k + 1 = 4 • 4 + 1 = 17.

Следующим за контуром с k = 4, от которого в интервал включается лишь полуконтур с L(M(4)) = 17, будет контур с k = 5 (его длина L(5) = 5 • 8 = 40), за ним с k = 6 (его длина L(6) = 6 • 8 = 48).

Вычислим суммарную длину полуконтура и 2-х контуров, т.е. длину интервала
L = 17 + 40 + 48 = 105 и сумму номеров контуров 4 / 2 + 5 + 6 = 13.
Для третьего интервала проделываются вычисления в том же порядке и получаем суммарную длину правого полуконтура из 8-го контура (k = 8) и полный k = 9 контур, т.е L(M(8)) = 4 • 8 +1 = 33, L(9) = 9 • 8 = 72 или L = 33 + 72 = 105. Сумма номеров контуров 8 / 2 + 9 = 13.

Для 4-го интервала, правому полуконтуру соответствует лишь половина номера контура, в котором он лежит, т.е.
k / 2 = 26 / 2 = 13.

Ф-инвариант. Видим, все 4 интервала характеризуются постоянным значением суммы номеров контуров и крайнего слева полуконтура, значением равным 13.

Ф-инвариантом СННЧ N называется половина номера контура k(N)/2, в котором это число является полуконтуром. Именно эту величину рассматриваем как ф-инвариант СННЧ N. Все выполненные вычисления для интервалов можно проделать в обратном порядке до представления интервала СННЧ разностью квадратов чисел разной четности. Получив представление числа N = Г_п (k) — Г_л(k) в виде разности границ интервала, которые всегда полные квадраты, выполняем разложение N на множители.

Границы интервалов находятся при условии, что известны номера контуров, формирующих интервал. Этот вопрос решается при представлении ф-инварианта специальной суммой (разбиением числа) слагаемых, являющихся номерами контуров, т.е. числами следующими подряд через единицу.