16.12.2019 08:24
DimsVs 9 2800 Источник
Добрый день!

В данной статье я попробую взглянуть по новому на алгоритм поиска общего решения системы линейных уравнений.

Задача, которой мы займемся звучит так.
Найти общее решение следующей системы уравнений

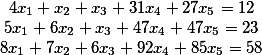
image

Такую задачу решают, приведя исходную систему к треугольному виду по методике Гаусса. Потом выбрав свободные переменные вычисляют общее решение.

Я хочу показать, как можно решать подобные системы другим способом. Насколько она известна и применяется где либо, я узнать не смог. Во всех публичных/популярных материалах, используется метод Гаусса.

Сразу скажу что решение конечно же не оптимально (по быстродействию), так как при вычислении векторного произведения, надо вычислять определитель матрицы, а это так или иначе вычисление треугольной матрицы.

Но решение красиво и наглядно, кроме этого легко видеть критерий при котором система не имеет решений.

В чем же суть методики?

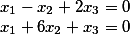
image

Решая эту систему как произведение двух векторов, мы получим

image

А следовательно, корни системы равны

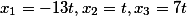
image

Для тех кто не верит, это легко проверяется подстановкой

Используем этот прием и рассмотрим, как же решаются такие системы с помощью векторных произведений.

Итак, у нас есть исходная система

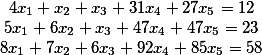
image

Перенесем свободные члены в левую часть
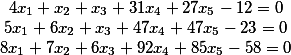
image

У нас получилось 6 столбцов.

На этом этапе не будем вводить новых сущностей и не используем в своей работе понятия ранга матрицы. (Прошу отнестись снисходительно)
Мы просто видим что уравнений 3, а переменных 5-ть. Следовательно общее решение будет использовать 5-3=2 независимых переменных.

На этом же шаге, мы можем определить, какие же из переменных будут свободными. Возьмем две переменных, которые будут правее всех, и назначим их свободными.
Note: Для других уравнений не всегда получается, что надо брать именно последние правые коэффициенты

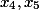
image

А теперь за три шага определяем фундаментальное решение исходной системы

Шаг 1. Здесь последняя колонка это свободные члены системы

image

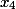
Шаг 2. Здесь последняя колонка это коэффициенты при переменной image

image

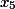
Шаг 3. Здесь последняя колонка это коэффициенты при переменной image

image

Нет необходимости подробно рассказывать откуда мы берем данные. Я думаю для читающих это очевидно. (Кто решал систему уравнений методом Крамера, найдут общие черты)

Интереснее то, что мы с этими «векторами» делать будем.

Разделим их на -81

получаем следующие три вектора

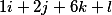
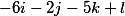
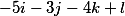
image

image

image

выстроим их в вертикаль и таким образом фундаментальное решение принимает вид

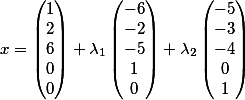
image

Великолепно! Не правда ли…

Для критерия разрешимости заданной системы уравнений в большинстве случаев используется правило Кронекера-Копелли, здесь же просто анализируется результат векторного произведения.

Если результирующий вектор имеет вид
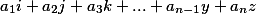
image
где 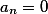image, а среди всех оставшихся есть хотя бы один не нулевой, то такая система решений не имеет

Если результирующий вектор имеет все нулевые коэффициенты, то это говорит о том, что или как минимум одно из уравнений есть линейное представление другого, и/или одна из переменных пропорциональна другой.

Эта статья первая, и хотелось бы услышать замечания, критику, пожелания в свой адрес.

Алгоритм и калькулятор создан еще в январе 2019 года и только сегодня я решил опубликовать информацию на Хабре.

Если примете в свой коллектив/общество, то следующая тема будет
— как находить общее решение системы диофантовых уравнений.

Комментарии (9)


  1. staticlab
    16.12.2019 11:47
    #21015956

    Вы изобрели метод Крамера.


    1. RISENT
      16.12.2019 17:47
      #21017898
      +1

      Скорее человек открыл(изобрел) для себя возможность писать статьи на хабр


      1. staticlab
        16.12.2019 18:16
        #21018014

        А ещё изобрёл сокращение ФРС )


  1. trofimovep
    16.12.2019 12:00
    #21016040

    Если вы не занимаетесь матаном, то открытие не тривиально и довольно интересно. Может даже в какой-то конкретной (производственной, не математической) задаче может помочь перебрать варианты какие-то (однако опять же, тут сводится к вычислительной мощности, коей на первый взгляд ваш метод не блистает)
    Однако должен заметить. В сути определитель матрицы является объемом гиперпараллелепипеда порожденного векторами матрицы. Вы выражаете этот объем в общем виде, и логично что данная пропорциональность таки будет обеспечивать равенство системы. Это известно еще с открытия собственных векторов. Общее решение никого не интересует, и уже придумали критерий получения оптимального решения переопределенных систем — минимальность невязки совместно с минимальностью нормы вектора, дающего эту невязку. Называется псевдорешение, и оно тоже вдоль и поперек ископано.


    1. DimsVs Автор
      16.12.2019 12:09
      #21016104

      Спасибо, за комментарий. Я решился написать об этом лишь потому, что этот метод, почему то достаточно редок в практическом применении. По крайней мере в интернете я все время натыкался на решение методом Гаусса, и ничего более. Возможно это моя ошибка, неумение правильно формулировать вопросы, возможно поисковых систем, которые вывод в ТОП однотипные клоны сайтов.
      Да и красиво все таки решается через вектора. Может пригодится, для понимания студентами…


      1. trofimovep
        16.12.2019 12:23
        #21016202

        Геометрия практически всегда красива) И втройне приятно открывать ее в повседневных вещах, таких как слау) А так, конечно, подобные темы не рассматриваются в университетских курсах, а для тех кто пишет книги — само собой очевидные (имею ввиду хорошие книги, монументальные, а не справочники или краткие пособия).


      1. SmallSnowball
        17.12.2019 21:06
        #21018628

        ну методов решения СЛАУ так-то очень много, вот неполный список
        ru.wikipedia.org/wiki/%D0%9A%D0%B0%D1%82%D0%B5%D0%B3%D0%BE%D1%80%D0%B8%D1%8F:%D0%9C%D0%B5%D1%82%D0%BE%D0%B4%D1%8B_%D1%80%D0%B5%D1%88%D0%B5%D0%BD%D0%B8%D1%8F_%D0%A1%D0%9B%D0%90%D0%A3

        Конкретно метод гаусса вообще на практике используется редко (по крайней мере на больших матрицах), он слишком медленный и очень неустойчивый для плохообусловленных матриц. На тех задачах, с которыми лично приходилось сталкиваться в 95% случаев применялись либо итерационные методы, либо один из методов через разложение матриц, вид разложения выбирается под исходную матрицу.


  1. mokhin-denis
    16.12.2019 13:50
    #21016726

    Существует множество применений СЛАУ. Например, метод конечных элементов. Он, в свою очередь, применяется для математического моделирования различных физических процессов. Например, лидер в индустрии CAE, компания ANSYS, Inc., на протяжении нескольких десятилетий создает пакет инженерного анализа ANSYS. Там число уравнений в системе исчисляется сотнями миллионов, а методы решения вшиты в решатели, которые загружают HPC-сервера под завязку.
    Об этом, в принципе, учат на узкопрофильных курсах ВУЗа (я, например, заканчивал физфак ННГУ). Плюс — об этом узнаешь на такой же узкопрофильной работе, где и пользуешься этими пакетами инженерного анализа. А если кому повезет — тот и сам создает CAE-пакеты (например, ЛОГОС).


    1. FGV
      16.12.2019 14:24
      #21016866

      Там число уравнений в системе исчисляется сотнями миллионов …

      Так оно и есть, только применительно к статье есть два отличия:


      1. СЛАУ полная, т.е. число уравнений = числу неизвестных;
      2. СЛАУ разряженная, т.е. очень много нулевых элементов.