
Звучит ли это знакомо: «Я начал заниматься веб разработкой после прохождения курсов»?
Возможно, вы хотите улучшить свои знания основ информатики в части структур данных и алгоритмов. Сегодня мы поговорим о некоторых наиболее распространенных структурах данных на примере JS.
1. Стек (вызовов) (Stack)
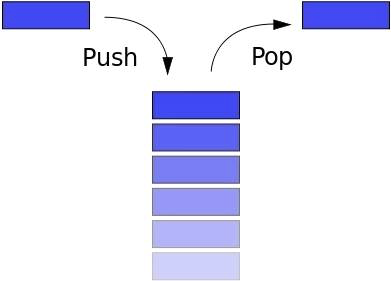
Стек следует принципу LIFO (Last In First Out — последним вошел, первым вышел). Если вы сложили книги друг на друга, и захотели взять самую нижнюю книгу, то сначала возьмете верхнюю, затем следующую и т.д. Кнопка «Назад» в браузере позволяет перейти (вернуться) на предыдущую страницу.
Стек имеет следующие методы:
- push: добавить новый элемент
- pop: удалить верхний элемент, вернуть его
- peek: вернуть верхний элемент
- length: вернуть количество элементов в стеке
Массив в JS имеет атрибуты стека, но мы построим его с нуля с помощью function Stack():
function Stack() {
this.count = 0
this.storage = {}
this.push = function(value) {
this.storage[this.count] = value
this.count++
}
this.pop = function() {
if (this.count === 0) return undefined
this.count--
let result = this.storage[this.count]
delete this.storage[this.count]
return result
}
this.peek = function() {
return this.storage[this.count - 1]
}
this.size = function() {
return this.count
}
}
2. Очередь (кью) (Queue)

Очередь напоминает стек. Разница состоит в том, что очередь следует принципу FIFO (First In First Out — первым вошел, первым вышел). Когда вы стоите в очереди, первый в ней всегда будет первым.
Очередь имеет следующие методы:
- enqueue: войти в очередь, добавить элемент в конец
- dequeue: покинуть очередь, удалить первый элемент и вернуть его
- front: получить первый элемент
- isEmpty: проверить, пуста ли очередь
- size: получить количество элементов в очереди
Массив в JS имеет некоторые атрибуты очереди, поэтому мы можем использовать его для демонстрации:
function Queue() {
let collection = []
this.print = function() {
console.log(collection)
}
this.enqueue = function(element) {
collection.push(element)
}
this.dequeue = function() {
return collection.shift()
}
this.front = function() {
return collection[0]
}
this.isEmpty = function() {
return collection.length === 0
}
this.size = function() {
return collection.length
}
}
Порядок очередности (приоритет)
Очередь имеет продвинутую версию. Присвойте каждому элементу приоритет, и элементы будут отсортированы соответствующим образом:
function PriorityQueue() {
...
this.enqueue = function(element) {
if (this.isEmpty()) {
collection.push(element)
} else {
let added = false
for (let i = 0; i < collection.length; i++) {
if (element[1] < collection[i][1]) {
collection.splice(i, 0, element)
added = true
break;
}
}
if (!added) {
collection.push(element)
}
}
}
}
Тестируем:
let pQ = new PriorityQueue()
pQ.enqueue([gannicus, 3])
pQ.enqueue([spartacus, 1])
pQ.enqueue([crixus, 2])
pQ.enqueue([oenomaus, 4])
pQ.print()
Результат:
[
[spartacus, 1],
[crixus, 2],
[gannicus, 3],
[oenomaus, 4]
]
3. Связный список (связанный, список узлов и ссылок или указателей) (Linked List)

Буквально, связный список — это цепочечная структура данных, где каждый узел состоит из двух частей: данных узла и указателя на следующий узел. Связный список и условный массив являются линейными структурами данных с сериализованным хранилищем. Отличия состоят в следующем:
| Критерий | Массив | Список |
|---|---|---|
| Выделение памяти | Статическое, происходит последовательно во время компиляции | Динамическое, происходит асинхронно во время запуска (выполнения) |
| Получение элементов | Поиск по индексу, высокая скорость | Поиск по всем узлам очереди, скорость менее высокая |
| Добавление/удаление элементов | В связи с последовательным и статическим распределением памяти скорость ниже | В связи с динамическим распределением памяти скорость выше |
| Структура | Одно или несколько направлений | Однонаправленный, двунаправленный или циклический |
Односвязный список имеет следующие методы:
- size: вернуть количество узлов
- head: вернуть первый элемент (head — голова)
- add: добавить элемент в конец (tail — хвост)
- remove: удалить несколько узлов
- indexOf: вернуть индекс узла
- elementAt: вернуть узел по индексу
- addAt: вставить узел в определенное место (по индексу)
- removeAt: удалить определенный узел (по индексу)
// узел
function Node(element) {
// данные
this.element = element
// указатель на следующий узел
this.next = null
}
function LinkedList() {
let length = 0
let head = null
this.size = function() {
return length
}
this.head = function() {
return head
}
this.add = function(element) {
let node = new Node(element)
if (head === null) {
head = node
} else {
let currentNode = head
while (currentNode.next) {
currentNode = currentNode.next
}
currentNode.next = node
}
length++
}
this.remove = function(element) {
let currentNode = head
let previousNode
if (currentNode.element !== element) {
head = currentNode.next
} else {
while (currentNode.element !== element) {
previousNode = currentNode
currentNode = currentNode.next
}
previousNode.next = currentNode.next
}
length--
}
this.isEmpty = function() {
return length === 0
}
this.indexOf = function(element) {
let currentNode = head
let index = -1
while (currentNode) {
index++
if (currentNode.element === element) {
return index
}
currentNode = currentNode.next
}
return -1
}
this.elementAt = function(index) {
let currentNode = head
let count = 0
while (count < index) {
count++
currentNode = currentNode.next
}
return currentNode.element
}
this.addAt = function(index, element) {
let node = new Node(element)
let currentNode = head
let previousNode
let currentIndex = 0
if (index > length) return false
if (index === 0) {
node.next = currentNode
head = node
} else {
while (currentIndex < index) {
currentIndex++
previousNode = currentNode
currentNode = currentNode.next
}
node.next = currentNode
previousNode.next = node
}
length++
}
this.removeAt = function(index) {
let currentNode = head
let previousNode
let currentIndex = 0
if (index < 0 || index >= length) return null
if (index === 0) {
head = currentIndex.next
} else {
while (currentIndex < index) {
currentIndex++
previousNode = currentNode
currentNode = currentNode.next
}
previousNode.next = currentNode.next
}
length--
return currentNode.element
}
}
4. Коллекция (значений) (Set)

Коллекция (множество) — одна из основных концепций математики: набор хорошо определенных и обособленных объектов. ES6 представил коллекцию, которая имеет некоторое сходство с массивом. Тем не менее, коллекция не допускает включения повторяющихся элементов и не содержит индексов.
Стандартная коллекция имеет следующие методы:
- values: вернуть все элементы в коллекции
- size: вернуть количество элементов
- has: проверить, имеется ли элемент в коллекции
- add: добавить элемент
- remove: удалить элемент
- union: вернуть область пересечения двух коллекций
- difference: вернуть отличия двух коллекций
- subset: проверить, является ли одна коллекция подмножеством другой
// дистанцируемся от Set в JS
function MySet() {
let collection = []
this.has = function(element) {
return (collection.indexOf(element) !== -1)
}
this.values = function() {
return collection
}
this.size = function() {
return collection.length
}
this.add = function(element) {
if (!this.has(element)) {
collection.push(element)
return true
}
return false
}
this.remove = function(element) {
if (this.has(element)) {
index = collection.indexOf(element)
collection.splice(index, 1)
return true
}
return false
}
this.union = function(otherSet) {
let unionSet = new MySet()
let firstSet = this.values()
let secondSet = otherSet.values()
firstSet.forEach(i => unionSet.add(i))
secondSet.forEach(i => unionSet.add(i))
}
this.intersection = function(otherSet) {
let intersectionSet = new MySet()
let firstSet = this.values()
firstSet.forEach(function(e) {
if (otherSet.has(e)) {
intersectionSet.add(e)
}
})
return intersectionSet
}
this.difference = function(otherSet) {
let differenceSet = new MySet()
let firstSet = this.values()
firstSet.forEach(function(e) {
if (!otherSet.has(e)) {
differenceSet.add(e)
}
})
return differenceSet
}
this.subset = function(otherSet) {
lat firstSet = this.values()
return firstSet.every(value => otherSet.has(value))
}
}
5. Хеш-таблица (таблица кэширования) (Hash Table)

Хеш-таблица — это структура данных, которая строится по принципу ключ-значение. Из-за высокой скорости поиска значений по ключам, она используется в таких структурах, как Map, Dictionary и Object. Как показано на рисунке, хеш-таблица имеет hash function, преобразующую ключи в список номеров, которые используются как имена (значения) ключей. Время поиска значения по ключу может достигать O(1). Одинаковые ключи должны возвращать одинаковые значения — в этом суть функции хэширования.
Хеш-таблица имеет следующие методы:
- add: добавить пару ключ/значение
- remove: удалить пару
- lookup: найти значение по ключу
function hash(string, max) {
let hash = 0
for (let i = 0; i < string.length; i++) {
hash += string.charCodeAt(i)
}
return hash % max
}
function HashTable() {
let storage = []
const storageLimit = 4
this.add = function(key, value) {
let index = hash(key, storageLimit)
if (storage[index] === undefined) {
storage[index] = [
[key, value]
]
} else {
let inserted = false
for (let i = 0; i < storage[index].len; i++) {
if (storage[index][i][0] === key) {
storage[index][i][1] = value
inserted = true
}
}
if (inserted === false) {
storage[index].push([key, value])
}
}
}
this.remove = function(key) {
let index = hash(key, storageLimit)
if (storage[index].length === 1 && storage[index][0][0] === key) {
delete storage[index]
} else {
for (let i = 0; i < storage[index]; i++) {
if (storage[index][i][0] === key) {
delete storage[index][i]
}
}
}
}
this.lookup = function(key) {
let index = hash(key, storageLimit)
if (storage[index] === undefined) {
return undefined
} else {
for (let i = 0; i < storage[index].length; i++) {
if (storage[index][i][0] === key) {
return storage[index][i][1]
}
}
}
}
}
6. Дерево (Tree)

Древовидная структура — это многослойная (многоуровневая) структура. Это также нелинейная структура, в отличие от массива, стека и очереди. Данная структура очень эффективна в части добавления и поиска элементов. Вот некоторые концепции древовидной структуры:
- root: корневой элемент, не имеет «родителя»
- parent node: прямой узел верхнего слоя (уровня), может быть только одним
- child node: прямой узел (узлы) нижнего уровня, может быть несколько
- siblings: дочерние элементы одного родительского узла
- leaf: узел без «детей»
- Edge: ветка или ссылка (связь) между узлами
- Path: путь (совокупность ссылок) от начального узла до целевого элемента
- Height of Tree (высота дерева): количество ссылок самого длинного пути от определенного элемента до узла, не имеющего потомков
- Depth of Node (глубина узла): количество ссылок от корневого узла до определенного элемента
- Degree of Node: количество потомков
Вот пример двоичного дерева поиска (Binary Search Tree, BST). Каждый узел имеет только двоих потомков, левый (дочерний) узел меньше текущего (родительского), правый — больше:

Методами данного дерева являются следующие:
- add: добавить узел
- findMin: получить минимальный узел
- findMax: получить максимальный узел
- find: найти определенный узел
- isPresent: проверить наличие определенного узла
- remove: удалить узел
class Node {
constructor(data, left = null, right = null) {
this.data = data
this.left = left
this.right = right
}
}
class BST {
constructor() {
this.root = null
}
add(data) {
const node = this.root
if (node === null) {
this.root = new Node(data)
return
} else {
const searchTree = function(node) {
if (data < node.data) {
if (node.left === null) {
node.left = new Node(data)
return
} else if (node.left !== null) {
return searchTree(node.left)
}
} else if (data > node.data) {
if (node.right === null) {
node.right = new Node(data)
return
} else if (node.right !== null) {
return searchTree(node.right)
}
} else {
return null
}
}
return searchTree(node)
}
}
findMin() {
let current = this.root
while (current.left !== null) {
current = current.left
}
return current.data
}
findMax() {
let current = this.root
while (current.right !== null) {
current = current.right
}
return current.data
}
find(data) {
let current = this.root
while (current.data !== data) {
if (data < current.data) {
current = current.left
} else {
current = current.right
}
if (current === null) {
return null
}
}
return current
}
isPresent(data) {
let current = this.root
while (current) {
if (data === current.data) {
return true
}
data < current.data ? current = current.left : current = current.right
}
return false
}
remove(data) {
const removeNode = function(node, data) {
if (node === null) return null
if (data === node.data) {
// потомки отсутствуют
if (node.left === null && node.right === null) return null
// отсутствует левый узел
if (node.left === null) return node.right
// отсутствует правый узел
if (node.right === null) return node.left
// имеется два узла
let tempNode = node.right
while (tempNode.left !== null) {
tempNode = tempNode.left
}
node.data = tempNode.data
node.right = removeNode(node.right, tempNode.data)
return node
} else if (data < node.data) {
node.left = removeNode(node.right, data)
return node
} else {
node.right = removeNode(node.right, data)
return node
}
}
this.root = removeNode(this.root, data)
}
}
Тестируем:
const bst = new BST()
bst.add(4)
bst.add(2)
bst.add(6)
bst.add(1)
bst.add(3)
bst.add(5)
bst.add(7)
bst.remove(4)
console.log(bst.findMin())
console.log(bst.findMax())
bst.remove(7)
console.log(bst.findMax())
console.log(bst.isPresent(4))
Результат:
1
7
6
false
7. Нагруженное (префиксное) дерево (Trie, читается как «try»)

Префиксное дерево — это разновидность поискового дерева. Данные в нем сохраняются последовательно (шаг за шагом) — каждый узел дерева представляет собой один шаг. Префиксное дерево используется в словарях, поскольку существенно ускоряет поиск.
Каждый узел дерева — буква алфавита, следование по ветке приводит к формированию слова. Оно также содержит «булевый индикатор» для определения того, что текущий узел является последней буквой.
Префиксное дерево имеет следующие методы:
- add: добавить слово в словарь
- isWord: проверить наличие слова
- print: вернуть все слова
// узел дерева
function Node() {
this.keys = new Map()
this.end = false
this.setEnd = function() {
this.end = true
}
this.isEnd = function() {
return this.end
}
}
function Trie() {
this.root = new Node()
this.add = function(input, node = this.root) {
if (input.length === 0) {
node.setEnd()
return
} else if (!node.keys.has(input[0])) {
node.keys.set(input[0], new Node())
return this.add(input.substr(1), node.key.get(input[0]))
} else {
return this.add(input.substr(1), node.keys.get(input[0]))
}
}
this.isWord = function(word) {
let node = this.root
while (word.length > 1) {
if (node.keys.has(word[0])) {
return false
} else {
node = node.keys.get(word[0])
word = word.substr(1)
}
}
return (node.keys.has(word) && node.keys.get(word).isEnd()) ? true : false
}
this.print = function() {
let words = new Array()
let search = function(node = this.root, string) {
if (node.keys.size !== 0) {
for (let letter of node.keys.keys()) {
search(node.keys.get(letter), string.concat(letter))
}
if (node.isEnd()) {
words.push(string)
}
} else {
string.length > 0 ? words.push(string) : undefined
return
}
}
search(this.root, new String())
return words.length > 0 ? words : null
}
}
8. Граф (график) (Graph)

Граф, также известный как сеть (Network), представляет собой коллекцию связанных между собой узлов. Бывает два вида графов — ориентированный и неориентированный, в зависимости от того, имеют ли ссылки направление. Графы используются повсеместно, например, для расчета наилучшего маршрута в навигационных приложениях или для формирования списка рекомендаций в социальных сетях.
Графы могут быть представлены в виде списка или матрицы.
Список
В данном случае все родительские узлы располагаются слева, а их дочерние элементы справа.

Матрица
В данном случае узлы распределяются по строкам и столбцам, пересечение строки и столбца показывает отношение между узлами: 0 означает, что узлы не связаны между собой, 1 — узлы связаны.

Поиск по графу осуществляется двумя методами — поиск в ширину (Breath-First-Search, BFS) и поиск в глубину (Depth-First-Search, DFS).
Рассмотрим BFS:
function bfs(graph, root) {
let nodesLen = {}
for (let i = 0; i < graph.length; i++) {
nodesLen[i] = Infinity
}
nodesLen[root] = 0
let queue = [root]
let current
while (queue.length !== 0) {
current = queue.shift()
let curConnected = graph[current]
let neighborIdx = []
let idx = curConnected.indexOf(1)
while (idx !== -1) {
neighborIdx.push(idx)
idx = curConnected.indexOf(1, idx + 1)
}
for (let i = 0; i < neighborIdx.length; i++) {
if (nodesLen[neighborIdx[i]] === Infinity) {
nodesLen[neighborIdx[i]] = nodesLen[current] + 1
queue.push(neighborIdx[i])
}
}
}
return nodesLen
}
Тестируем:
let graph = [
[0, 1, 1, 1, 0],
[0, 0, 1, 0, 0],
[1, 1, 0, 0, 0],
[0, 0, 0, 1, 0],
[0, 1, 0, 0, 0]
]
console.log(bfs(graph, 1))
Результат:
{
0: 2,
1: 0,
2: 1,
3: 3,
4: Infinity
}
На этом у меня все. Надеюсь, вы нашли для себя что-то полезное. Счастливого кодинга!


White_Scorpion
Хм… Я не сильно много работаю с JS, но даже я в курсе, что обычный Array это два в одном — сразу и стэк и очередь. В зависимости от применяемых к нему функций.
И смысл первых двух обёрток — исключительно "приятственный глазу вид"?
dolovar
Статья для тех, кто «started frontend development by completing part-time courses». Туториал, в общем.
Тут не про JS, а про знакомство со структурами данных — если вы работаете девом, но не знаете чем очередь от стека отличается, то
что вы делаете на Хабревотвозьмите книжку и наконец прочитайтетут примерно расписанона единственном языке который вы хоть немного знаете.На западе девелоперы любят пополнять свое портфолио подобными публикациями, полезно для карьеры.
funca
Могу ошибаться, но заголовок оригинала «8 Common Data Structures in Javascript» лучше было бы перенести как "… на JavaScript". Материал носит скорее иллюстративный характер, помогающий знакомым с этим языком погрузиться в тему ADT на первых этапах обучения. Читайте Кнута и не используйте примеры из учеников в продакшене :).
"… в JavaScript" часть из описанных структур реализована нативно, поэтому нет особого смысла городить абстракции над абстракциями. В поисках же эффективных реализаций исписаны сотни страниц и конца этому пока не видно.
VolCh
Его можно использовать в качестве стэка или очереди, но это будет лишь иммитацией поведения.