Tarantool — это сервер приложений и база данных. Серверная часть написана на C, а пользователю предоставлен Lua-интерфейс для работы с ним. Кроме того, Tarantool — это opensource-продукт, а значит, исходный код лежит в открытом доступе, и можно свободно разрабатывать и распространять ПО на основе Tarantool.
Но сегодня рассказ будет немного о другом: об эксперименте, о попытке написать свою структуру данных для поиска (Z-order curve) и встроить её в существующую экосистему Tarantool.
Я разработчик в Tarantool Solution Team, не занимаюсь непосредственной разработкой Tarantool, а отношусь к активным пользователям. Поэтому, для меня этот эксперимент — попытка разобраться, как Tarantool работает на низком уровне.
Что такое Tarantool и где он хранит данные?
Что такое Tarantool? В мире баз данных он позиционируется как in-memory технология. Движок memtx позволяет хранить все ваши данные в оперативной памяти, и удовлетворяет при этом всем принципам ACID.
Аналогом реляционных таблиц в Tarantool являются спейсы (space), которые предназначены для хранения кортежей (tuples). В отличие от реляционных таблиц, кортежи в спейсе в общем случае могут быть произвольной длины. Для их хранения должна быть создана структура данных поиска, при этом ключ поиска — первичный ключ, всегда уникальный.
Можно построить и дополнительные структуры — вторичные индексы, хранящие лишь указатель на кортеж. Вторичный индекс может быть не уникальным, однако это лишь внешнее поведение, видимое пользователю. К любому не уникальному индексу неявно добавляются поля первичного индекса. Так обеспечивается стабильность сортировки кортежей внутри индекса.
Tarantool поддерживает разные типы индексов:
- В-первую очередь, в B-Tree (а если совсем точно, то B+*-Tree). О структуре B-деревьев написано очень много [B-Tree]. Отмечу лишь, что данные хранятся в отсортированном виде, к тому же можно искать по префиксу проиндексированного ключа.
- Индекс на основе hash-таблицы. Подходит, если вам не нужны выборки интервалов. Доступ по полному ключу. В отличие от B-дерева, время доступа к элементу не логарифмическое, а постоянное. Этот индекс всегда уникальный.
- R-Tree. Этот тип индекса уже более специализированный. Предназначен для хранения «многомерных» данных, например, географических координат. Поддерживает индексацию полей только одного типа — массив. Это массив наших условных координат, которые являются обычными числами с плавающей запятой. При этом в плане запросов он достаточно функционален. Позволяет искать точки, лежащие внутри и вне заданной границы, а также ближайших соседей.
- Bitset. Пожалуй, самый таинственный для меня индекс. Ознакомьтесь с ним, если вдруг вам потребуется хранить битовые массивы в спейсах и выполнять запросы, используя битовые маски.
Кривая Z-порядка, или кривая Мортона
Откуда возникла идея написать свой индекс, причем довольно экзотический?
Однажды я наткнулся на статьи Amazon [1, 2], в которых рассказывалось о такой структуре, как кривая Z-порядка, или кривая Мортона. Это рецепт расположения «многомерных» данных внутри плоской структуры (Z-order curve), которая затем укладывается в B-дерево. Такой подход должен помочь избежать сплошного сканирования данных. В целом многомерными данными можно считать информацию о любом объекте, обладающем некоторым набором характеристик. Например, рост, вес, размер ноги и т.д. человека. В большинстве баз данных для подобных целей используется R-Tree.
Немного о том, как устроена кривая Z-порядка.

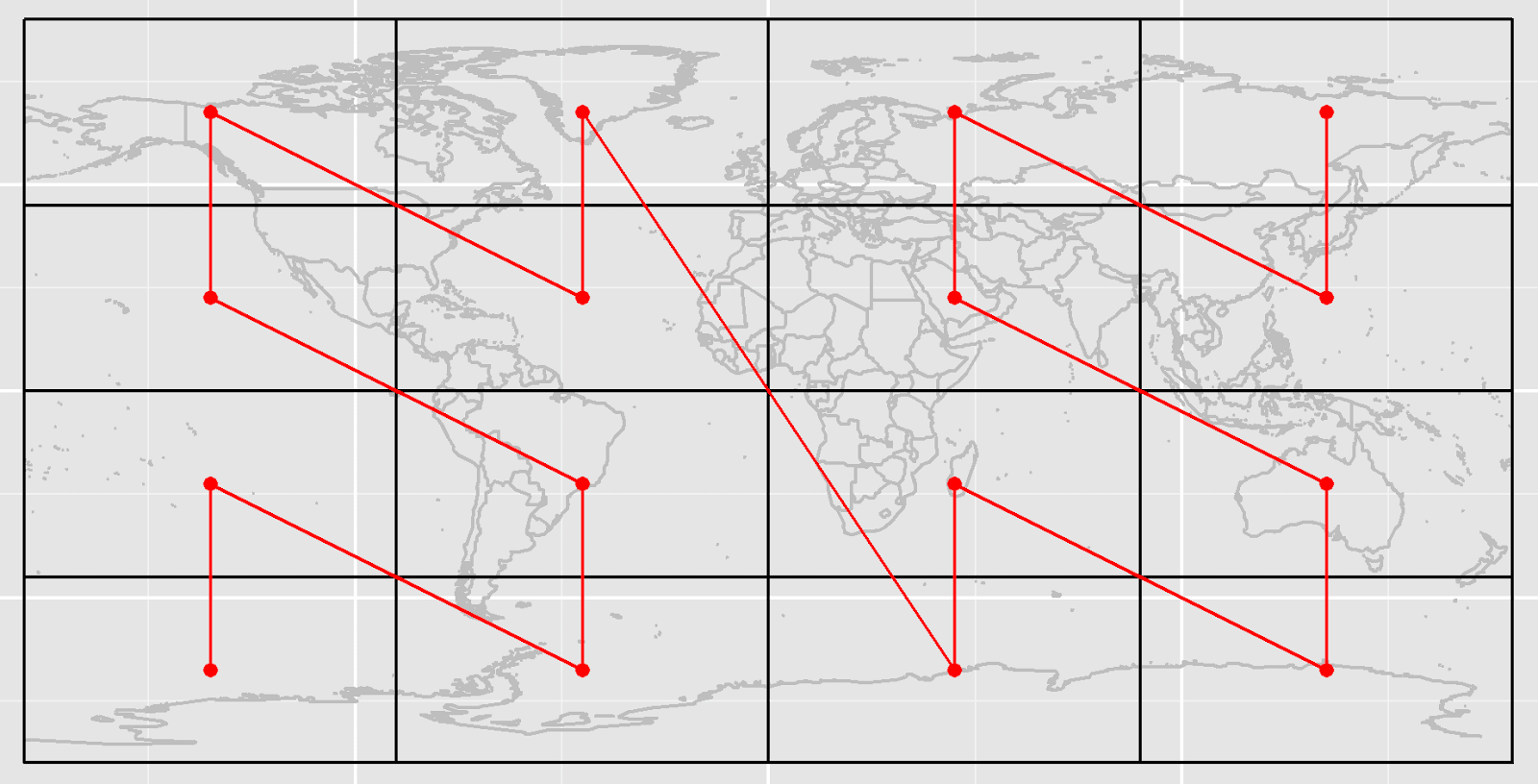
Кривая Z-порядка, она же кривая Мортона, получается путем перемежения битов координат точки в пространстве. Полученные таким образом Z-адреса обладают свойством локальности. Точки, находившиеся рядом в многомерном пространстве, будут по-прежнему располагаться рядом и при отображении на плоскую линию.
Схематически подобное перемешивание выглядит так:

Как это работает? Мы ограничиваем некоторую область в пространстве — гиперкуб (в двумерном пространстве будет прямоугольник) — с помощью двух точек, лежащих на диагонали, которые отображаются в две точки на прямой. И получаем неприятный побочный эффект: часть точек выходит за границу ограничивающего прямоугольника:

То есть мы не можем просто итерироваться по этой кривой. Но, вооружившись специальным алгоритмом, мы можем при выходе за границу делать прыжок, возвращаясь обратно в область поиска. Как только мы выходим за крайнюю точку кривой (назовем её upper_bound), поиск закончен.
При работе с B-Tree мы имели бы набор интервалов, и этот запрос привел бы к последовательному сканированию B-дерева, что заняло бы очень много времени при большом наборе данных.
Мой интерес подогревали и другие публикации об этой кривой. Например, о том, как она была интегрирована в TransBase [3], проприетарную БД. И, к сожалению своему, я не нашел никаких open source-реализаций этой структуры.
Лежащее в основе этой кривой B-Tree обладает рядом преимуществ перед R-Tree. Например, лучшей заполняемостью и компактностью. Недостатки: большинство используемых алгоритмов ограничено по процессору. Для сравнения я решил воспользоваться Tarantool: интересовали скорости чтения/вставки, а также потребление памяти. Нельзя не упомянуть, что похожая тема уже поднималась на Хабре, но для небольших размерностей (2-3) и применительно к дисковой БД PostgreSQL [ZcurvePostgres].
Что потребовалось для встраивания в Tarantool?
Я находил простенькие реализации этой структуры для размерности 2-3, но мне хотелось сравнить производительность с существующим R-Tree-индексом, поэтому ограничиваться малыми размерностями мне не хотелось. Я выбрал такую же размерность, как и у R-Tree — 20. Для этого мне был нужен битовый массив с поддержкой некоторых примитивных операций: извлечения/изменения бита, сдвига, логических операций OR/AND.
Для прототипа я взял найденную open source-реализацию, но довольно быстро пришел к тому, что мне не нужен битовый массив общего назначения: длина ключа всегда кратна 64, поэтому часть операций существенно упрощается. Я написал собственную реализацию на базе того, что у меня было. Кроме того, вместо использования системных функций выделения памяти я начал использовать специальные аллокаторы, реализованные в Tarantool [4].
Пожалуй, сердце индекса — это набор алгоритмов для работы с Z-кривой. А именно, вычисление Z-адреса (с помощью специальных lookup-таблиц), проверка принадлежности Z-адреса к области поиска и обнаружение первого вхождения в область поиска, начиная с указанной точки. Если хорошо поискать в сети, то можно найти научные публикации с описанием этих алгоритмов, поэтому всё, что мне оставалось, это их реализовать, отладить и, по возможности, оптимизировать. Хранить Z-адреса предполагалось внутри уже реализованного B-дерева, использующегося для TREE-индекса.
Как организована работа с данными?
В самом общем случае нам приходит tuple. Это массив данных в формате message pack. И в идеальном случае мы должны были бы просто вычленить проиндексированные поля, перемешать их биты и вставить адрес с указателем на кортеж внутрь B-дерева.
Однако всё было бы так просто, если бы мы работали только с типом unsigned, когда отсортированные битовые представления чисел соответствовали бы отсортированным числам в натуральном представлении. У знаковых целых чисел свои правила представления, у чисел с плавающей запятой — свои. И это пришлось приводить к общему знаменателю. За счет того, что мы храним Z-адрес отдельно от самих данных, мы можем выполнять любые преобразования над нашими ключами, главное — сохранять порядок сортировки. Это можно делать с помощью несложных битовых манипуляций. Например, для целых знаковых чисел можно просто инвертировать старший байт. Для других типов тоже есть подобные, пусть и чуть более сложные, преобразования.
Все числовые типы умещаются в 8 байтов, поэтому результирующий ключ будет размера N * 8 байтов, где N — размерность нашего пространства. Что делать со строками?
Довольно частая ситуация при работе со строками — префиксный поиск. И его вполне можно поддержать. Первые 8 байтов строки вполне могут быть использованы в качестве ключа. Если строка короче, то её можно дополнить нулями. Поддержка строк накладывает фундаментальное ограничение на наш индекс: мы теряем уникальность. Даже если строки различаются в девятом байте, то с точки зрения системы они всё равно будут одинаковыми.
Посмотрим на код.
API индекса состоит из определенного набора методов. Рассматривать каждый в отдельности мы не будем, пройдемся лишь по самым основным, а именно — по операциям поиска и вставки.
get — поиск элемента по полному ключу. Работает лишь для уникальных индексов. Наш индекс не может быть уникальным, поэтому функция заменяется специальной generic-версией, возвращающей ошибку «Unsupported index feature». replace — вставка элемента. Рассмотрим подробнее.static int
memtx_zcurve_index_replace(struct index *base, struct tuple *old_tuple,
struct tuple *new_tuple, enum dup_replace_mode mode,
struct tuple **result)
{
(void)mode;
struct memtx_zcurve_index *index = (struct memtx_zcurve_index *)base;
if (new_tuple) {
struct memtx_zcurve_data new_data;
new_data.tuple = new_tuple;
new_data.z_address = extract_zaddress(new_tuple,
&index->bit_array_pool, index);
struct memtx_zcurve_data dup_data;
dup_data.tuple = NULL;
dup_data.z_address = NULL;
int tree_res = memtx_zcurve_insert(&index->tree, new_data,
&dup_data);
if (tree_res) {
diag_set(OutOfMemory, MEMTX_EXTENT_SIZE,
"memtx_zcurve_index", "replace");
return -1;
}
if (dup_data.tuple != NULL) {
*result = dup_data.tuple;
z_value_free(&index->bit_array_pool, dup_data.z_address);
return 0;
}
}
if (old_tuple) {
struct memtx_zcurve_data old_data, deleted_value;
old_data.tuple = old_tuple;
old_data.z_address = extract_zaddress(old_tuple,
&index->bit_array_pool, index);
memtx_zcurve_delete_value(&index->tree, old_data, &deleted_value);
z_value_free(&index->bit_array_pool, old_data.z_address);
z_value_free(&index->bit_array_pool, deleted_value.z_address);
}
*result = old_tuple;
return 0;
}На что стоит обратить внимание?
С точки зрения индекса не существует операций
update, delete, insert и replace. Вся их логика выполняется в этом методе, получающем старый и новый кортежи, а также mode — информацию о том, является индекс уникальным или нет. Наш индекс не может быть уникальным, поэтому никаких дополнительных проверок не требуется и можно сразу вставлять кортеж.memtx_zcurve_insert и memtx_zcurve_delete_value — методы B-дерева, которое уже было реализовано в Tarantool и используется в обычном TREE-индексе. На них мы не будем отдельно останавливаться. В отличие от обычного TREE мы храним не просто tuple, а ещё и z-адрес — перемешанные биты проиндексированных частей. За это отвечает функция extract_zadress.create_iterator — из Lua мы обращаемся к этому методу в случае select’а и pairs’а.static struct iterator *
memtx_zcurve_index_create_iterator(struct index *base, enum iterator_type type,
const char *key, uint32_t part_count)
{
struct memtx_zcurve_index *index = (struct memtx_zcurve_index *)base;
struct memtx_engine *memtx = (struct memtx_engine *)base->engine;
assert(part_count == 0 || key != NULL);
if (type != ITER_EQ && type != ITER_ALL && type != ITER_GE) {
diag_set(UnsupportedIndexFeature, base->def,
"requested iterator type");
return NULL;
}
uint8_t index_dim = base->def->key_def->part_count;
if (part_count == 0) {
/*
* If no key is specified, downgrade equality
* iterators to a full range.
*/
type = ITER_GE;
key = NULL;
} else if (index_dim * 2 == part_count
&& type != ITER_ALL) {
/*
* If part_count is twice greater than key_def.part_count
* set iterator to range query
*/
type = ITER_GE;
}
struct tree_iterator *it = mempool_alloc(&memtx->zcurve_iterator_pool);
if (it == NULL) {
diag_set(OutOfMemory, sizeof(struct tree_iterator),
"memtx_zcurve_index", "iterator");
return NULL;
}
iterator_create(&it->base, base);
it->pool = &memtx->zcurve_iterator_pool;
it->base.next = tree_iterator_start;
it->base.free = tree_iterator_free;
it->type = type;
if (part_count == 0 || type == ITER_ALL) {
it->lower_bound = zeros(&index->bit_array_pool, index_dim);
it->upper_bound = ones(&index->bit_array_pool, index_dim);
} else if (type == ITER_EQ) {
it->lower_bound = mp_decode_key(&index->bit_array_pool,
key, index_dim, index);
it->upper_bound = NULL;
} else if (base->def->key_def->part_count == part_count) {
it->lower_bound = mp_decode_key(&index->bit_array_pool,
key, index_dim, index);
it->upper_bound = ones(&index->bit_array_pool, index_dim);
} else if (base->def->key_def->part_count * 2 == part_count) {
it->lower_bound = z_value_create(&index->bit_array_pool, index_dim);
it->upper_bound = z_value_create(&index->bit_array_pool, index_dim);
mp_decode_part(key, part_count, index, it->lower_bound, it->upper_bound);
} else {
unreachable();
}
it->tree_iterator = memtx_zcurve_invalid_iterator();
it->current.tuple = NULL;
it->current.z_address = NULL;
return (struct iterator *)it;
}В зависимости от переданного ключа мы вычисляем нижнюю и верхнюю границу запроса. Однако пока что этот итератор ни на что не указывает. Всего существует несколько типов итераторов. В нашем случае это ALL — получение всех элементов; EQ — получение элементов, z-адрес которых совпадает с переданным; и GE — выборка элементов в гиперкубе.
destroy — удаление индекса. В случае со вторичным индексом просто освобождает ту память, которая выделялась под структуру поиска. А если индекс первичный, то физически удаляет хранящиеся кортежи.Весь код доступен по адресу: https://github.com/olegrok/tarantool/tree/z-order-curve-index
Давайте посмотрим, что получилось, и подведем итоги.
space = box.schema.space.create('myspace', { engine = 'memtx' })
pk = space:create_index('primary', { type = 'tree', parts = {{1, 'unsigned'}}, unique = true})
sk = space:create_index('secondary', { type = 'zcurve', parts = {{2, 'unsigned'}, {3, 'unsigned'}}})
for i=0,5 do for j=0,5 do space:insert{i * 6 + j, i, j} end end
-- returns all tuples
pk:select{}
-- (2 <= x <= 3) and (3 <= y <= 5)
sk:select{2, 3, 3, 5}
---
- — [15, 2, 3]
- [21, 3, 3]
- [16, 2, 4]
- [22, 3, 4]
- [17, 2, 5]
- [23, 3, 5]
…
-- (x == 2) and (y == 3)
sk:select{2, 3}
---
- — [15, 2, 3]
-- (2 <= x <= 3)
sk:select({2, 3, box.NULL, box.NULL})
---
- — [12, 2, 0]
- [18, 3, 0]
- [13, 2, 1]
- [19, 3, 1]
- [14, 2, 2]
- [20, 3, 2]
- [15, 2, 3]
- [21, 3, 3]
- [16, 2, 4]
- [22, 3, 4]
- [17, 2, 5]
- [23, 3, 5]
...
-- (x >= 2) and (y >= 3)
sk:select({2, box.NULL, 3, box.NULL})
---
- — [15, 2, 3]
- [21, 3, 3]
- [27, 4, 3]
- [33, 5, 3]
- [16, 2, 4]
- [22, 3, 4]
- [17, 2, 5]
- [23, 3, 5]
- [28, 4, 4]
- [34, 5, 4]
- [29, 4, 5]
- [35, 5, 5]
...А что с производительностью?
Оказалось, что всё не так радужно, как я описывал.
Начиная с какого-то момента кривая Z-порядка начинает существенно проседать по скорости доступа к данным. perf top показывал, что основное время тратится на проверку принадлежности точки к области поиска и вычисление очередной точки, к которой необходимо прыгнуть. Обе операции имеют линейную сложность в зависимости от длины ключа — с увеличением размерности увеличивается и длина.

Из приятного — потребление памяти в 2-3 раза меньше и вставка чуть быстрее, чем у R-Tree. Что не особо релевантно, ведь измерения производились с выключенным WAL. Во-первых, в production-среде в случае сбоя отключенный WAL может привести к потере данных. Во-вторых, несмотря на то, что запись в WAL использует батчевый подход, это всё равно запись на диск, которая в тысячи раз медленнее, чем работа с оперативной памятью.


Также интересно сравнить с B-деревом. Тут, как и предполагалось, кривая будет быстрее, чем полное сканирование и проверка каждой точки на принадлежность к заданной области. Даже не смотря на то, что проверка является более легковесной, чем в случае кривой Z-порядка, где всё сводится к побитовому сравнению.
Цифры на графике отличаются по порядку от R-Tree — тест был слегка изменен.

Для теста я генерировал набор точек и сравнивал длительность при запросе с использованием Z-кривой и при обычном сканировании.
Подведем итоги
В мире in-memory эта структура показала себя не лучшим образом, однако у неё все равно есть достоинства:
- Занимает меньше места.
- Типизирована, в отличие от R-Tree (актуально только для Tarantool).
- К ней стоит присмотреться, если есть только B-Tree и нужно делать многомерные запросы (не актуально для Tarantool).
Это был интересный эксперимент. Вряд ли предложенное мной решение когда-нибудь станет частью Tarantool. Тем не менее, не стоит бояться экспериментировать. И если у вас есть какие-то предложения и решения, то не бойтесь делиться ими.
Источники
[B-Tree]:
Индексы в PostgreSQL — 4 / Блог компании Postgres Professional / Хабр
B-tree / Хабр
Структура данных B-дерево / Блог компании OTUS. Онлайн-образование / Хабр
[ZcurvePostgres]:
Про Z-оrder и R-дерево / Хабр
Z-order vs R-tree, продолжение / Хабр
[1] Z-Order Indexing for Multifaceted Queries in Amazon DynamoDB: Part 1 | AWS Database Blog
[2] Z-order indexing for multifaceted queries in Amazon DynamoDB: Part 2 | AWS Database Blog
[3] Integrating the UB-Tree into a Database System Kernel
[4] https://github.com/tarantool/small


kostja
olegrok я рад что получилось закончить прототип. Основное преимущество и назначение индекса — многокритериальный поиск, в приложениях типа yandex.market. Производительность з-кривой деградирует линейно с увеличением числа размерностей, в то время как производительность r-tree — полиномиально. Я бы попробовал протестировать на реальных данных и задачах — проиндексиров базу cian или продуктовый каталог yandex.market. В настоящее время в open source нет субд с хорошей поддержкой многокритериального поиска, связано это в первую очередь с тем что сложно завести транзакционный менеджер для таких индексов. Уверен, что это будет востребованно — вопрос просто доведения технологии до ума и популяризации.