09.07.2020 14:33
36 7600 Источник


Armored Warfare: Проект Армата — бесплатный танковый онлайн-экшн, разрабатываемый Allods Team, игровой студией MY.GAMES. Несмотря на то, что игра сделана на CryEngine, достаточно популярном движке с неплохим realtime render’ом, для нашей игры приходится многое дорабатывать и создавать с нуля. В этой статье я хочу рассказать о том, как мы реализовывали хроматическую аберрацию для вида от первого лица, и что это такое.

Что такое хроматическая аберрация?


Хроматическая аберрация – это дефект линзы, при котором в одну и ту же точку приходят не все цвета. Это связано с тем, что показатель преломления среды зависит от длины волны света (см. дисперсия). Вот так, например, выглядит ситуация, когда линза не болеет хроматической аберрацией:


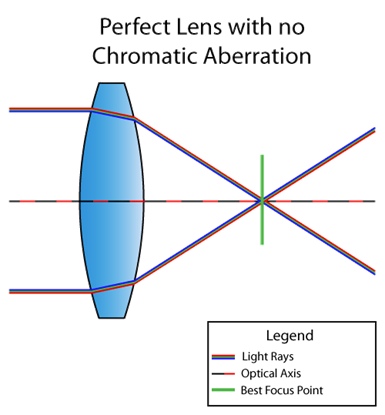
А вот уже линза с дефектом:


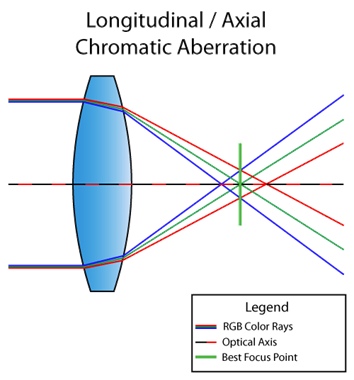
Кстати, ситуация выше называется продольной (или осевой) хроматической аберрацией. Возникает она в случае, когда различные длины волн не сходятся в одной и той же точке фокальной плоскости после прохождения через линзу. Тогда дефект виден по всей картинке:


На картинке выше можно увидеть, что из-за дефекта выделяются фиолетовый и зелёный цвета. Не видно? А на этой картинке?


Также существует боковая (или поперечная) хроматическая аберрация. Возникает она в случае, когда свет падает под углом к линзе. По итогу, различные длины волн света сходятся в разных точках фокальной плоскости. Вот вам картинка для понимания:


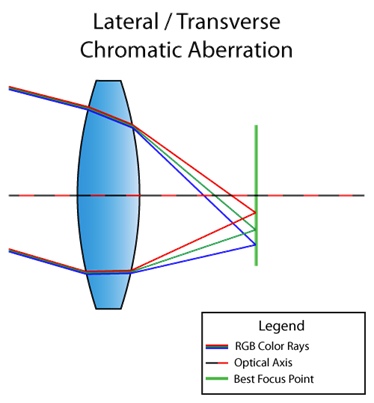
Можно уже по схеме увидеть, что в итоге мы получаем полноценное разложение света от красного до фиолетового. В отличии от продольной, боковая хроматическая аберрация никогда не проявляется в центре, только ближе к краям изображения. Чтобы вы понимали, о чём я, вот вам ещё одна картинка из интернета:


Ну, раз с теорией мы закончили, давайте переходить к сути.

Боковая хроматическая аберрация с учётом разложения света


Начну я всё же с того, что отвечу на вопрос, который мог возникнуть в голове у многих из вас: «а разве в CryEngine нет реализованной хроматической аберрации?» Есть. Но применяется она на этапе пост-процессинга в одном шейдере с sharpening, а алгоритм выглядит так (ссылка на код):

screenColor.r = shScreenTex.SampleLevel( shPointClampSampler, (IN.baseTC.xy - 0.5) * (1 + 2 * psParams[0].x * CV_ScreenSize.zw) + 0.5, 0.0f).r;
screenColor.b = shScreenTex.SampleLevel( shPointClampSampler, (IN.baseTC.xy - 0.5) * (1 - 2 * psParams[0].x * CV_ScreenSize.zw) + 0.5, 0.0f).b;

Что, в принципе, работает. Но у нас игра про танки. Нам этот эффект нужен только для вида от первого лица, и только для красоты, то есть чтобы в центре всё было в фокусе (привет боковой аберрации). Поэтому текущая реализация не устраивала как минимум тем, что её эффект был виден по всей картинке.

Так выглядела сама аберрация (внимание на левую сторону):


А так она выглядела, если перекрутить параметры:


Поэтому, своей целью мы поставили:

  1. Реализовать боковую хроматическую аберрацию, чтобы возле прицела всё было в фокусе, а по бокам если не видно характерных цветных дефектов, то хотя бы чтобы было размыто.
  2. Сэмплировать текстуру, умножая RGB-каналы на коэффициенты, соответствующие конкретной длине волны. Об этом я ещё не рассказывал, поэтому сейчас может быть не совсем понятно, о чём этот пункт. Но мы его обязательно рассмотрим во всех подробностях позже.

Для начала рассмотрим общий механизм и код для создания боковой хроматической аберрации.

half distanceStrength = pow(length(IN.baseTC - 0.5), falloff);
half2 direction = normalize(IN.baseTC.xy - 0.5);
half2 velocity = direction * blur * distanceStrength;

Итак, сначала строится круговая маска, отвечающая за дистанцию от центра экрана, потом считается направление от центра экрана, а далее это всё перемножается с blur. Blur и falloff – это параметры, которые передаются извне и являются просто множителями для настройки аберрации. Также извне прокидывается параметр sampleCount, который отвечает не только за количество сэмплов, но и, по сути, за шаг между точками сэмплирования, так как

half2 offsetDecrement = velocity * stepMultiplier / half(sampleCount);

Теперь нам осталось просто проходиться sampleCount раз от данной точки текстуры, сдвигаясь каждый раз на offsetDecrement, домножать каналы на соответствующие веса волн и делить на сумму этих весов. Что ж, пришла пора поговорить о втором пункте нашей глобальной цели.

Видимый спектр света лежит в диапазоне длин волн от 380 нм (фиолетовый) до 780 нм (красный). И, о чудо, длину волны можно конвертировать в RGB-палитру. На Python код, который занимается этой магией, выглядит так:

def get_color(waveLength):
    if waveLength >= 380 and waveLength < 440:
        red = -(waveLength - 440.0) / (440.0 - 380.0)
        green = 0.0
        blue  = 1.0
    elif waveLength >= 440 and waveLength < 490:
        red   = 0.0
        green = (waveLength - 440.0) / (490.0 - 440.0)
        blue  = 1.0
    elif waveLength >= 490 and waveLength < 510:
        red   = 0.0
        green = 1.0
        blue  = -(waveLength - 510.0) / (510.0 - 490.0)
    elif waveLength >= 510 and waveLength < 580:
        red   = (waveLength - 510.0) / (580.0 - 510.0)
        green = 1.0
        blue  = 0.0
    elif waveLength >= 580 and waveLength < 645:
        red   = 1.0
        green = -(waveLength - 645.0) / (645.0 - 580.0)
        blue  = 0.0
    elif waveLength >= 645 and waveLength < 781:
        red   = 1.0
        green = 0.0
        blue  = 0.0
    else:
        red   = 0.0
        green = 0.0
        blue  = 0.0
    
    factor = 0.0
    if waveLength >= 380 and waveLength < 420:
        factor = 0.3 + 0.7*(waveLength - 380.0) / (420.0 - 380.0)
    elif waveLength >= 420 and waveLength < 701:
        factor = 1.0
    elif waveLength >= 701 and waveLength < 781:
        factor = 0.3 + 0.7*(780.0 - waveLength) / (780.0 - 700.0)
 
    gamma = 0.80
    R = (red   * factor)**gamma if red > 0 else 0
    G = (green * factor)**gamma if green > 0 else 0
    B = (blue  * factor)**gamma if blue > 0 else 0
    
    return R, G, B

В итоге мы получаем следующее распределение цвета:


Если коротко, то на графике показано сколько и какого цвета содержится в волне с конкретной длиной. По оси ординат у нас как раз получаются те самые веса, о которых я говорил ранее. Теперь мы можем реализовать полностью алгоритм, с учётом оговоренного ранее:

half3 accumulator = (half3) 0;
half2 offset = (half2) 0;
half3 WeightSum = (half3) 0;
half3 Weight = (half3) 0;
half3 color;
half waveLength;
 
for (int i = 0; i < sampleCount; i++)
{
    waveLength = lerp(startWaveLength, endWaveLength, (half)(i) / (sampleCount - 1.0));
    Weight.r = GetRedWeight(waveLength);
    Weight.g = GetGreenWeight(waveLength);
    Weight.b = GetBlueWeight(waveLength);
        
    offset -= offsetDecrement;
        
    color = tex2Dlod(baseMap, half4(IN.baseTC + offset, 0, 0)).rgb;
    accumulator.rgb += color.rgb * Weight.rgb; 
        
    WeightSum.rgb += Weight.rgb;
}
 
OUT.Color.rgb = half4(accumulator.rgb / WeightSum.rgb, 1.0);

То есть идея в том, что чем больше у нас sampleCount, тем меньше шаг у нас между точками сэмпла, и тем подробнее дисперсируем свет (учитываем больше волн с различными длинами).

Если до сих пор непонятно, то давайте рассмотрим конкретный пример, а именно на нашу первую попытку, и я объясню, что брать за startWaveLength и endWaveLength, и как будут реализованы функции GetRed(Green, Blue)Weight.

Аппроксимация всего диапазона видимого спектра


Итак, из графика выше мы знаем примерное соотношение и примерные значения RGB палитры для каждой длины волны. Например, для длины волны 380 нм (фиолетовый цвет) (см. тот же график) видим, что RGB(0.4, 0, 0.4). Вот именно эти значения мы и берём за веса, о которых я говорил ранее.

Попробуем теперь избавиться от функции получения цвета полиномом четвёртой степени, чтобы вычисления были дешевле (мы не студия Pixar, а игровая студия: чем дешевле вычисления, тем лучше). Этот полином четвёртой степени должен аппроксимировать полученные графики. Для построения полинома я воспользовался библиотекой SciPy:

wave_arange = numpy.arange(380, 780, 0.001)
red_func = numpy.polynomial.polynomial.Polynomial.fit(wave_arange, red, 4)

В итоге получается следующий результат (я разбил на 3 отдельных графика, соответствующих каждому отдельному каналу, чтобы проще было сравнить с точным значением):




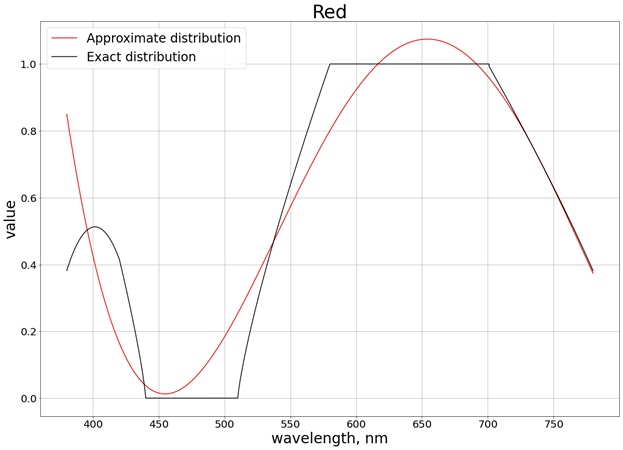
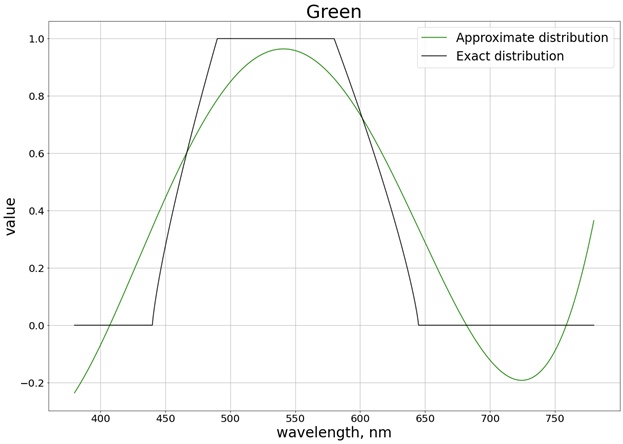
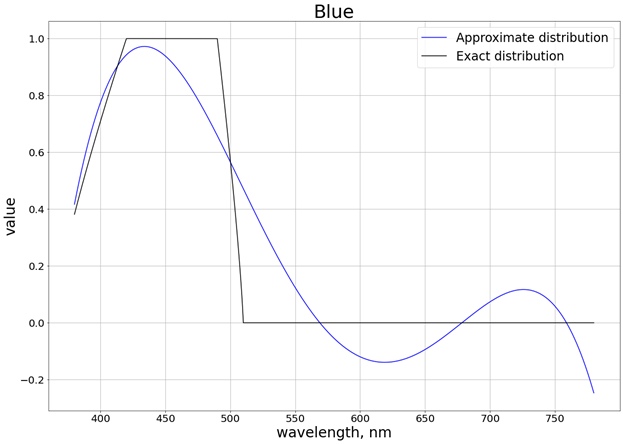
Для того чтобы значения не выходили за предел отрезка [0, 1], используем функцию saturate. Для красного цвета, например, получается функция:

half GetRedWeight(half x)
{
    return saturate(0.8004883122689207 + 
    1.3673160565954385 * (-2.9000047500568042 + 0.005000012500149485 * x) - 
    1.244631137356407 * pow(-2.9000047500568042 + 0.005000012500149485 * x, 2) - 1.6053230172845554 * pow(-2.9000047500568042 + 0.005000012500149485*x, 3)+ 1.055933936470091 * pow(-2.9000047500568042 + 0.005000012500149485*x, 4));
}

Недостающие параметры startWaveLength и endWaveLength в данном случае являются 780 нм и 380 нм, соответственно. Результат на практике с sampleCount=3 получается следующий (см. края картинки):


Если же подкрутить значения, увеличить sampleCount до 400, то всё становится лучше:


К сожалению, у нас realtime render, в котором мы не можем позволить 400 сэмплов (примерно 3-4) в одном шейдере. Поэтому мы немного сократили диапазон длин волн.

Аппроксимация по части диапазона видимого спектра


Возьмём такой диапазон, чтобы у нас по итогу были и чисто красный, и чисто синий цвета. От хвостика красного цвета слева тоже отказываемся, так как он очень сильно влияет на итоговый полином. В итоге, получаем распределение на отрезке [440, 670]:


Также нет необходимости интерполировать по всему отрезку, так как мы теперь можем получить полином только того участка, где значение меняется. Например, для красного цвета, это отрезок [510, 580], где значение веса меняется от 0 до 1. В этом случае можно получить полином второго порядка, который потом функцией saturate также свести к диапазону значений [0, 1]. По всем трём цветам мы получаем следующий результат с учётом сатурации:


В итоге мы получаем, например, для красного цвета следующий полином:

half GetRedWeight(half x)
{
    return saturate(0.5764348105166407 + 
    0.4761860550080825 * (-15.571636738012254 + 0.0285718367412005 * x) - 
    0.06265740390367036 * pow(-15.571636738012254 + 0.0285718367412005 * x, 2));
}

А на практике с sampleCount=3:


При этом с перекрученными настройками получается примерно тот же результат, как и при сэмплировании по всему диапазону видимого спектра:


Таким образом, полиномами второй степени мы получили неплохой результат на диапазоне волн от 440 нм до 670 нм.

Оптимизация


Помимо оптимизации расчётов полиномами, можно оптимизировать работу шейдера, опираясь на механизм, который мы заложили в основу нашей боковой хроматической аберрации, а именно, не проводить расчёты в области, где суммарное смещение не выходит за рамки текущего пикселя, иначе мы сэмплируем один и тот же пиксель, и получаем его же.

Выглядит это примерно так:

bool isNotAberrated = abs(offsetDecrement.x * g_VS_ScreenSize.x) < 1.0 && abs(offsetDecrement.y * g_VS_ScreenSize.y) < 1.0;
if (isNotAberrated)
{
    OUT.Color.rgb = tex2Dlod(baseMap, half4(IN.baseTC, 0, 0)).rgb;
    return OUT;
}

Оптимизация небольшая, но очень гордая.

Заключение


Сама боковая хроматическая аберрация выглядит очень круто, прицелу в центре этот дефект не мешает. Идея с разложением света по весам – очень интересный эксперимент, который может дать совершенно другую картинку, если ваш движок или игра позволяет больше трёх сэмплов. В нашем же случае можно было не заморачиваться и придумать другой алгоритм, так как даже с оптимизациями мы не можем позволить себе много сэмплов, а, например, между 3 и 5 сэмплами разница не очень видна. Вы же можете сами поэкспериментировать с описанным методом и посмотреть на результаты.