
Развивая наш неослабевающий интерес к серьезной, можно сказать, академической литературе, мы добрались и до теории категорий. Эта тема в знаменитом изложении Бартоша Милевского уже фигурировала на Хабре и к настоящему времени может похвастаться такими показателями:

Тем более приятно, что нам удалось обнаружить сравнительно свежий материал (январь 2020), служащий отличным и при этом максимально кратким введением в теорию категорий. Надеемся, что нам удастся заинтересовать вас этой темой
Если мы с вами, уважаемый читатель, сталкивались со схожими проблемами, то и вас когда-то мучил вопрос «черт возьми, что такое монада?!» Затем вы гуглили этот вопрос, незаметно падая в кроличью нору абстрактной математики, запутываясь в функторах, моноидах, категориях, пока не замечали, что уже забыли, какой вопрос вас сюда завел. Такой опыт может быть весьма ошеломительным, если ранее вы в глаза не видели языков для функционального программирования, но не волнуйтесь! Я за вас проштудировал многие страницы густой математики и посмотрел целые часы лекций на эту тему. Таким образом, чтобы избавить вас от такой необходимости, я резюмирую здесь эту тему, а также покажу, каким образом можно применить теорию категорий, чтобы вы могли прямо с сегодняшнего дня мыслить (и писать код) в функциональном стиле.
Эта статья предназначена для всех, кто считает себя «новичком» в области функционального программирования и только начинает работать со Scala, Haskell или другим подобным языком. Дочитав эту статью, вы почувствуете себя немного увереннее в трактовке основ теории категорий и выявлении ее принципов «на местности». Кроме того, если вы когда-либо собирались попробовать свои силы в теоретической математике, воздержитесь от прямого упоминания тех концепций, которые здесь затрагиваются. Как правило, о каждой из них можно сказать гораздо больше, чем написано здесь, но для любознательного программиста хватит и этой статьи.
Основы
Итак, что же такое категория, и как она связана с программированием? Как и многие концепции, используемые в программировании, категория – это весьма простая вещь с вычурным названием. Это всего лишь размеченный ориентированный граф с некоторыми дополнительными ограничениями. Каждый из узлов в категории называется «объект», а каждое из ее ребер называется «морфизм».
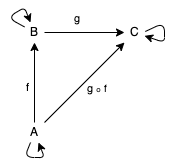
Как вы уже могли догадаться, не всякий ориентированный граф является категорией; чтобы граф считался категорией, должны быть соблюдены некоторые дополнительные критерии. На следующей картинке отметим, что у каждого объекта есть морфизм, указывающий сам на себя. Это тождественный морфизм, и у каждого объекта должен быть такой, чтобы граф считался категорией. Далее обратите внимание, что у объекта
A есть морфизм f, указывающий на B, и, аналогично, у объекта B есть морфизм g, указывающий на C. Поскольку существует путь от A до B и от B до C, очевидно, существует путь от A до C, верно? Это следующее требование к категории: для морфизмов обязательно должна выполняться ассоциативная композиция, таким образом, что для морфизма f: A = > B и g: B = > C существует морфизм h = g(f): A = > C.Эти выкладки уже могут показаться немного отвлеченными, поэтому давайте рассмотрим пример, удовлетворяющий этому определению и написанный на Scala.
trait Rock
trait Sand
trait Glass
def crush(rock: Rock): Sand
def heat(sand: Sand): GlassДумаю, на таком примере взаимосвязи покажутся немного проще. Стирание камней в песок – это морфизм, преобразующий объект
rock в объект sand, а выплавка стекла из песка – это морфизм, преобразующий объект sand в объект glass. В таком случае, композиция этих отношений определенно будет иметь вид val glass: Glass = heat(crush(rock))Также существуют функции тождества (определяемые в
Predef на Scala), так как для любого объекта не составляет труда написать функцию, возвращающую этот же объект. Следовательно, эта система является категорией, хотя и довольно простой. Более глубокое знакомство с категориями
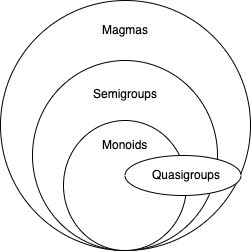
Сейчас мы немного углубимся в терминологию теории категорий и начнем с категории под названием магмы. Если вы пока не слишком знакомы с этой базовой концепцией, поясню, что магма – это просто бинарная операция, то есть, операция над двумя значениями, в результате которой получается новое значение. Чтобы не вдаваться в детали, я не стану приводить здесь доказательство того, что множество всех бинарных операций на самом деле является категорией, но тем, кого интересуют подробности, рекомендую почитать следующую статью Бартоша Милевского. Вся арифметика от сложения до умножения относится к подкатегориям, объединенным магматической категорией (см. схему).
Здесь действует следующий порядок наследования:
- 1. Магма: все бинарные операции
- 2. Полугруппы: все бинарные операции, являющиеся ассоциативными
- o Ассоциативная операция: порядок вычисления не имеет значения.
- 3. Моноиды: все бинарные операции, являющиеся ассоциативными и имеющие нейтральный элемент
- o Нейтральный элемент: значение, которое в комбинации с другим значением возвращает это значение (aka единичный элемент)
Так, возвращаясь к нашему более раннему примеру, как сложение, так и умножение являются моноидами, поскольку они ассоциативны
(a + (b + c) = (a + b) + c) и имеют единичный элемент (a x 1 = 1 x a = a). В последнем кружочке на этой диаграмме находятся квазигруппы, для которых могут действовать иные принципы вложения, нежели для полугрупп или моноидов. Квазигруппы – это бинарные операции, которые являются обратимыми. Объяснить это свойство не так просто, поэтому отсылаю вас к серии статей Марка Симана, посвященной этой теме. Бинарная операция является обратимой, когда для любых значений a и b существуют такие значения x и y, которые позволяют преобразовать a в b. Знаю, звучит мудрено. Чтобы было понятно, давайте рассмотрим следующий пример вычитания:val x = a - b
val y = a + b
assert(a - x == b)
assert(y - a == b)Обратите внимание:
y не участвует в вычитании как таковом, но пример все равно считается. Объекты в категории абстрагируются и могут быть практически чем угодно; в данном случае важно, что для любых a и b, которые могут быть сгенерированы, эти утверждения остаются верными.Типы в контексте
Независимо от конкретной дисциплины, тема типов должна быть понятна любому, кто понимает смысл типов данных в программировании. Целое число, булево значение, значение с плавающей точкой и так далее – все это типы, но как бы вы описали словами идеальный платоновский тип? В своей книге Category Theory for Programmers, превратившейся в серию статей для блога, Милевский описывает типы просто как «множества значений». Например, булеан – конечное множество, содержащее значения “true” (истина) и “false” (ложь). Символ (char) – это конечное множество всех числобуквенных символов, а строка (string) – бесконечное множество char.
Проблема в том, что в теории категорий мы стремимся отойти от множеств и мыслить в терминах объектов и морфизмов. Но от того факта, что типы – это попросту множества, никуда не уйти. К счастью, в теории категорий находится место для этих множеств, поскольку наши объекты – это абстракции, и могут представлять что угодно. Следовательно, мы имеем полное право сказать, что наши объекты – это множества, и далее рассматривать наши программы на Scala как категории, где типы – это объекты, а функции – это морфизмы. Многим это может казаться до боли очевидным; в конце концов, в Scala мы привыкли иметь дело с объектами, но это стоит обозначить явно.
Если вам доводилось работать с объектно-ориентированным языком, например, с Java, то вам наверняка знакома концепция обобщенных типов. Это такие вещи как
LinkedList или, в случае Scala, Option[T], где T представляет базовый тип данных, сохраненный в некоторой структуре. Что, если бы мы захотели создать отображение с одного типа на другой, таким образом, чтобы структура первого типа сохранилась? Добро пожаловать в мир функторов, определяемых как отображения между категориями, позволяющие сохранять структуру. В программировании обычно приходится работать с подкатегорией функторов, так называемыми эндофункторами, которые помогают отобразить категорию саму на себя. Поэтому просто оговорюсь, что, говоря о функторах, я имею в виду эндофункторы.В качестве примера функтора давайте рассмотрим тип Scala
Option[T] в сочетании с нашим предыдущим примером, в котором упоминались камень, песок и стекло:val rockOpt: Option[Rock] = Some(rock)Выше у нас тип
Rock в том виде, как мы определили его ранее, но обернутый в Option. Это обобщенный тип (и не только, подробнее об этом ниже), сообщающий нам, что объект – это либо конкретная сущность, которую мы ищем, либо None, что можно сравнить с null в других языках.Если бы мы не использовали функторы, то можно было бы представить, как мы применяем функцию
crush() к Rock, что потребовало бы прибегнуть к оператору if для обработки ситуации, в которой Option является None.var sandOpt: Option[Sand] = None
if(rockOpt != None) {
sandOpt = Some(crush(rockOpt.get))
}Можно сказать, что это отступление в сторону, но, пожалуйста, не используйте var – такой код на Scala плох по нескольким причинам. Опять же, возвращаясь к теме: в Java или C# это не представляло бы проблемы. Вы проверяете, относится ли ваше значение к тому типу, который вы ожидали увидеть, и делаете с ним что хотите. Но, обладая силой функторов, все можно сделать несколько элегантнее, при помощи функции
map():val sandOpt: Option[Sand] = rockOpt.map(crush)Бум, одна строка – и все готово. Можно было бы уложить в одну строку и первый пример, воспользовавшись тернарным оператором или чем-то подобным, на настолько лаконично у вас бы не получилось. Этот пример действительно чудесен в своей простоте. Вот, что здесь происходит:
map() принимает функцию и отображает эту функцию (в математическом смысле) саму на себя. Структура Option сохраняется, но теперь в ней содержится либо Sand, либо None, вместо Rock либо None. Это можно проиллюстрировать примерно так:
Обратите внимание, как красиво все выстраивается, все до одного объекты и морфизмы сохраняются в обеих системах. Следовательно, морфизм в центре – это функтор, представляющий отображение с
T на Option[T].Все вместе
Теперь мы наконец-то можем вернуться к исходному вопросу «черт возьми, что такое монада»? Существует ответ, на который можно наткнуться вслепую, если просто попытаться его нагуглить, и он звучит так: монада – это просто моноид в категории эндофункторов, после чего часто следует весьма саркастическое замечание, «а в чем проблема-то?» Как правило, таким образом пытаются шутливо показать, насколько все сложно в этой теме, но на самом деле не все так страшно – ведь мы уже разобрались, что означает эта фраза. Давайте еще раз разберем ее шаг за шагом.
Во-первых, нам известно, что моноиды – это ассоциативные бинарные операции, в каждой из которых содержится нейтральный (единичный) элемент. Во-вторых, мы знаем, что эндофункторы позволяют отобразить категорию саму на себя, с сохранением структуры. Таким образом, монада – это просто некий тип-обертка (как в примере с обобщенными типами выше), поддерживающий некоторый метод для принятия функции и отображения ее самой на себя.
List – это монада, Option (как тот, что мы рассмотрели выше) – это монада, а кто-то даже может сказать вам, что и Future – это тоже монада. Пример:val l: List[Int] = List(1, 2, 3)
def f(i: Int) = List(i, i*2, i*3)
println(l.flatMap(f)) // вывод: List(1, 2, 3, 2, 4, 6, 3, 6, 9)Обманчиво просто, не правда ли? Как минимум, должно оставаться ощущение, что здесь несложно все уловить, даже если на первый взгляд не вполне понятно, в чем польза такой концепции.


germn
Расскажите, когда следующая распродажа будет, а то я на недавнюю опоздал — обидно! :)