Явное лучше неявного.
В данной статье рассматривается задача пересчета неявных связей элементов графа в явные. В общем-то ответом является одна несложная формула, которая приведена под номером 3. Все остальные слова понадобились для того, чтобы рассказать, откуда она берется, и как ею пользоваться. Я написал данную статью для тех, кто интересуется анализом данных вообще и графов в частности.
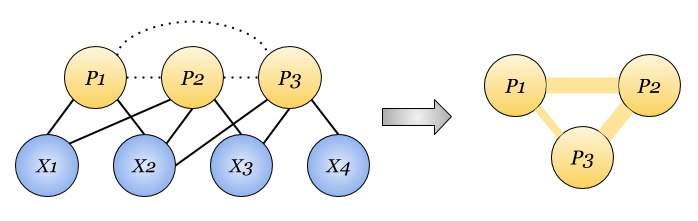
Что такое неявная связь элементов? Это связь, возникающая вследствие связи элементов одного множества (типа, вида, рода) с элементами другого. При этом как правило явные связи между элементами внутри множеств отсутствуют. Пример таких связей приведен на рисунке выше.
Если приглядеться, то увидим, что вокруг нас полно таких связей.
Сотрудники и проекты. Связь сотрудника с проектом отражает степень его вовлеченности в проект. Разные сотрудники могут быть связаны с разными проектами («многие-ко-многим», да). На основании того, кто в каких проектах участвует, можно определить величину связи сотрудников между собой. Очевидно, что сотрудники, участвующие в одних и тех же проектах, должны быть связаны сильнее.
Посты и комментарии. В соцсетях люди пишут посты и комментарии к ним. Можно выяснить связь людей на основании того, в каких постах они оставляют комментарии.
Подобным же образом можно рассчитать связи сотрудников компании на основе ее документооборота.
Товары в накладных. Можно определить близость товаров на основании их попадания в одну накладную (или чек). Чем чаще товары встречаются вместе — тем они ближе друг к другу. Близость товаров можно использовать для рекомендаций.
Слова и документы. Чем больше в двух документах одних и тех же слов, — тем ближе данные документы. В другую сторону тоже работает, — чем чаще два слова встречаются в одном и том же документе, — тем они ближе.
Буквы и слова. Чем чаще встречаются буквы в одном слове, — тем более эти буквы связаны.
Люди и фото. Чем чаще люди встречаются на общей фотографии, — тем они ближе.
Думаю, примеров достаточно. Во всех примерах присутствуют элементы двух множеств разного типа. При этом элементы каждого множества можно считать независимыми (несвязанными друг с другом). Сотрудники явно не связаны с другими сотрудниками, документы явно не связаны с другими документами. Это определенное упрощение, но оно не критично.
Поскольку есть связи, то очевидно, что будут и графы. И в самом деле в виду распространенности подобных связей для образуемых ими графов есть специальное название — двудольные. Две доли графа — это и есть два независимых множества, связанных между собой.
Часто (но необязательно) размер одной доли (множества) во много раз превосходит размер другой. Например, если количество сотрудников исчисляется десятками, то количество документов, в которых они отметились — может исчисляться сотнями или тысячами. Букв в русском алфавите 33, но слов, которые они образуют — тысячи.
Очевидно, что чем больше элементов в графе, — тем неудобнее его анализировать. Поэтому возникает задача «свертки связей», — надо преобразовать двудольный граф в однодольный (однородный), оставив только одно множество элементов (обычно это меньшая доля). Полученный однородный граф можно анализировать в более комфортных условиях.
Но как выполнить свертку связей наиболее обоснованно с точки зрения математики? Тут надо немного углубиться в метрические пространства.
Вообще для того, чтобы использовать преобразование двудольного графа в однодольный, не требуется знаний о метрических пространствах. Поэтому данный раздел пометили звездочкой — он для любопытных.
Обычно про графы рассказывают в дискретной математике, а понятие пространств дают в линейной алгебре. В результате в голове графы находятся в одном месте, а пространства в другом. Надо сделать небольшое усилие, чтобы понять, что графы — это не только комбинаторика и алгоритмы. Граф (здесь и далее для простоты будем считать графы связными и ненаправленными) задает метрическое пространство. Вершины графа — это элементы базиса данного пространства. Расстояния между элементами (наличие которых и выделяет метрические пространства среди прочих) можно определить на основании связей вершин графа между собой.
В графе данные расстояния обычно называют резистивными. Почему «резистивными». Потому что, если в качестве графа выбрать электрическую сеть (где связь элементов — это величина, обратная сопротивлению между узлами), то значение резистивной дистанции совпадает со значением эффективного сопротивления между данными узлами. Чем больше расстояние — тем больше сопротивление. Вроде бы логично.
Математически резистивные дистанции соответствуют квадратам обычных (геометрических) расстояний. Величины связей и резистивных дистанций взаимно обратны. Можно определять расстояния на основе связей вершин, а можно наоборот, — величину связей между элементами на основании дистанций между ними.
Вернемся к долям. В связном графе можно рассчитать расстояния между любыми его вершинами. А раз так, то можно выделить из графа произвольное подмножество его вершин и найти такие связи между вершинами, которые бы обеспечили те же расстояния между ними, что и в исходном графе. Математически это преобразование означает переход от пространства к подпространству с сохранением скалярного произведения на элементах подпространства.
Таким образом можно преобразовать расстояния между элементами одной доли в значения связей между ними. Логика такая:
Исходный двудольный граф -> (задает) -> Расстояния между элементами доли -> (по которым можно рассчитать) -> Искомый однодольный граф.
На самом деле нет необходимости считать сами расстояния. Надо лишь найти такое преобразование графа в подграф, при котором резистивные расстояния между элементами подграфа не меняются. Это классическая задача отображения пространства в подпространство. Отметим, например, что известное преобразование «Треугольник-Звезда» является частным (и упрощенным) случаем такого преобразования.
Итак, одна из долей нашего графа задает подпространство, которое мы хотим определить. «Определить» в данном случае — это значит построить матрицу смежности подграфа на основании матрицы смежности исходного графа.
В матрице смежности двудольного графа можно выделить четыре блока, соответствующие связям долей. Поскольку внутри каждой доли связи отсутствуют, то из всех блоков остается только два взаимно симметричных — связь элементов одной доли с элементами другой. Такой блок называют также матрицей бисмежности, подчеркивая, что тут связываются два независимых множества.
Вместо матриц лучше сразу использовать термин «тензоры» — это ближе к реляционным таблицам и базам данных, в которых, обычно и содержатся исходные данные. Тензор бисмежности — это просто таблица с двумя измерениями (индексами) «Откуда», «Куда» и одним ресурсом — «Вес связи». Для графа на рисунке тензор бисмежности будет таким:
Мы привели явный вид данного тензора, чтобы показать, — нет особой необходимости трактовать преобразования на языке графов и матриц. В конечном счете все сводится к операциям реляционной алгебры.
Элементы множества, связи между которыми хотим определить, будем обозначать как (и ), а все множество как .
Для элементов дополнительного к нему множества (доли) используем символы (и ). Это могут быть документы, в которых сотрудники оставляют комментарии, или товарные накладные, если ищем связи между товарами.
Тензор связей (матрица бисмежности) между множествами считается заданным.
Для каждого объекта (вершины графа) можно определить его степень. Это количество связей данного объекта. Например, для документов степень — это количество ссылок на него (сколько в нем всего комментариев или товаров), для слова — его длина (количество букв). Степени дополнительной доли обозначим , значения степеней равны сумме по колонкам матрицы смежности :
Здесь — свертка тензора по измерению . Эквивалентна произведению матрицы на кортеж из единиц .
В общем случае элементы доли могут быть тоже связаны (на рисунке такие связи обозначены пунктиром). Учтем это введением матрицы связей (смежности) . Если граф двудольный, то данные связи (и их матрица) равны нулю.
Искомую матрицу результирующих связей между элементами множества (доли) обозначим как .
Тогда справедливо следующее утверждение (лемма):
Величина результирующих связей между элементами множества равна сумме исходных и наведенных связей:
При этом матрица наведенных связей представляет собой следующую квадратичную форму (это и есть основная формула статьи):
Здесь — фундаментальная матрица, которая определяется как обращение минора матрицы-лапласиана:
Все приведенные выше формулы пригодны для любого (неориентированного) графа, как двудольного, так и нет. Они вытекают из формул обращения блочных матриц.
Фишка двудольных графов заключается в том, что минор лапласиана для доли графа представляет собой диагональную матрицу, составленную из степеней элементов (поскольку нет связей между элементами). Поэтому обращение данного минора сводится просто к обратным значениям степеней :
В итоге вместо затратной процедуры обращения матрицы здесь имеем дело с обычным делением. Если речь идет о тысячах элементов, то данный нюанс имеет значение. Собственно ради его подчеркивания мы и написали данную статью.
Подставляя обратные степени в (3), получаем формулу преобразования матрицы би-смежности в матрицу смежности заданной доли:
Если тензор бисмежности задан в виде реляционной таблицы, то выполнить преобразование (6) можно одним sql-запросом. Ну а в библиотеках типа python pandas данное преобразование может быть записано одной строкой действий над объектом dataframe.
Для приведенного выше тензора бисмежности степени элементов будут такими: . Соответственно, диагональ фундаментальной матрицы будет равна обратным значениям: . Подставляя ее в формулу (6), получаем тензор наведенных связей (для удобства приводим целочисленные значения):
На этом все. В следующей статье рассмотрим, для чего все это нужно, и какую полезную информацию можно извлечь из полученного подграфа.
Более подробная математика преобразования пространства графа в подпространство приведена здесь.

В данной статье рассматривается задача пересчета неявных связей элементов графа в явные. В общем-то ответом является одна несложная формула, которая приведена под номером 3. Все остальные слова понадобились для того, чтобы рассказать, откуда она берется, и как ею пользоваться. Я написал данную статью для тех, кто интересуется анализом данных вообще и графов в частности.
Постановка задачи
Что такое неявная связь элементов? Это связь, возникающая вследствие связи элементов одного множества (типа, вида, рода) с элементами другого. При этом как правило явные связи между элементами внутри множеств отсутствуют. Пример таких связей приведен на рисунке выше.
Если приглядеться, то увидим, что вокруг нас полно таких связей.
Сотрудники и проекты. Связь сотрудника с проектом отражает степень его вовлеченности в проект. Разные сотрудники могут быть связаны с разными проектами («многие-ко-многим», да). На основании того, кто в каких проектах участвует, можно определить величину связи сотрудников между собой. Очевидно, что сотрудники, участвующие в одних и тех же проектах, должны быть связаны сильнее.
Посты и комментарии. В соцсетях люди пишут посты и комментарии к ним. Можно выяснить связь людей на основании того, в каких постах они оставляют комментарии.
Подобным же образом можно рассчитать связи сотрудников компании на основе ее документооборота.
Товары в накладных. Можно определить близость товаров на основании их попадания в одну накладную (или чек). Чем чаще товары встречаются вместе — тем они ближе друг к другу. Близость товаров можно использовать для рекомендаций.
Слова и документы. Чем больше в двух документах одних и тех же слов, — тем ближе данные документы. В другую сторону тоже работает, — чем чаще два слова встречаются в одном и том же документе, — тем они ближе.
Буквы и слова. Чем чаще встречаются буквы в одном слове, — тем более эти буквы связаны.
Люди и фото. Чем чаще люди встречаются на общей фотографии, — тем они ближе.
Думаю, примеров достаточно. Во всех примерах присутствуют элементы двух множеств разного типа. При этом элементы каждого множества можно считать независимыми (несвязанными друг с другом). Сотрудники явно не связаны с другими сотрудниками, документы явно не связаны с другими документами. Это определенное упрощение, но оно не критично.
Поскольку есть связи, то очевидно, что будут и графы. И в самом деле в виду распространенности подобных связей для образуемых ими графов есть специальное название — двудольные. Две доли графа — это и есть два независимых множества, связанных между собой.
Часто (но необязательно) размер одной доли (множества) во много раз превосходит размер другой. Например, если количество сотрудников исчисляется десятками, то количество документов, в которых они отметились — может исчисляться сотнями или тысячами. Букв в русском алфавите 33, но слов, которые они образуют — тысячи.
Очевидно, что чем больше элементов в графе, — тем неудобнее его анализировать. Поэтому возникает задача «свертки связей», — надо преобразовать двудольный граф в однодольный (однородный), оставив только одно множество элементов (обычно это меньшая доля). Полученный однородный граф можно анализировать в более комфортных условиях.
Но как выполнить свертку связей наиболее обоснованно с точки зрения математики? Тут надо немного углубиться в метрические пространства.
Пространства и подпространства графов (*)
Вообще для того, чтобы использовать преобразование двудольного графа в однодольный, не требуется знаний о метрических пространствах. Поэтому данный раздел пометили звездочкой — он для любопытных.
Обычно про графы рассказывают в дискретной математике, а понятие пространств дают в линейной алгебре. В результате в голове графы находятся в одном месте, а пространства в другом. Надо сделать небольшое усилие, чтобы понять, что графы — это не только комбинаторика и алгоритмы. Граф (здесь и далее для простоты будем считать графы связными и ненаправленными) задает метрическое пространство. Вершины графа — это элементы базиса данного пространства. Расстояния между элементами (наличие которых и выделяет метрические пространства среди прочих) можно определить на основании связей вершин графа между собой.
В графе данные расстояния обычно называют резистивными. Почему «резистивными». Потому что, если в качестве графа выбрать электрическую сеть (где связь элементов — это величина, обратная сопротивлению между узлами), то значение резистивной дистанции совпадает со значением эффективного сопротивления между данными узлами. Чем больше расстояние — тем больше сопротивление. Вроде бы логично.
Математически резистивные дистанции соответствуют квадратам обычных (геометрических) расстояний. Величины связей и резистивных дистанций взаимно обратны. Можно определять расстояния на основе связей вершин, а можно наоборот, — величину связей между элементами на основании дистанций между ними.
Вернемся к долям. В связном графе можно рассчитать расстояния между любыми его вершинами. А раз так, то можно выделить из графа произвольное подмножество его вершин и найти такие связи между вершинами, которые бы обеспечили те же расстояния между ними, что и в исходном графе. Математически это преобразование означает переход от пространства к подпространству с сохранением скалярного произведения на элементах подпространства.
Таким образом можно преобразовать расстояния между элементами одной доли в значения связей между ними. Логика такая:
Исходный двудольный граф -> (задает) -> Расстояния между элементами доли -> (по которым можно рассчитать) -> Искомый однодольный граф.
На самом деле нет необходимости считать сами расстояния. Надо лишь найти такое преобразование графа в подграф, при котором резистивные расстояния между элементами подграфа не меняются. Это классическая задача отображения пространства в подпространство. Отметим, например, что известное преобразование «Треугольник-Звезда» является частным (и упрощенным) случаем такого преобразования.
Матрицы и тензоры
Итак, одна из долей нашего графа задает подпространство, которое мы хотим определить. «Определить» в данном случае — это значит построить матрицу смежности подграфа на основании матрицы смежности исходного графа.
В матрице смежности двудольного графа можно выделить четыре блока, соответствующие связям долей. Поскольку внутри каждой доли связи отсутствуют, то из всех блоков остается только два взаимно симметричных — связь элементов одной доли с элементами другой. Такой блок называют также матрицей бисмежности, подчеркивая, что тут связываются два независимых множества.
Вместо матриц лучше сразу использовать термин «тензоры» — это ближе к реляционным таблицам и базам данных, в которых, обычно и содержатся исходные данные. Тензор бисмежности — это просто таблица с двумя измерениями (индексами) «Откуда», «Куда» и одним ресурсом — «Вес связи». Для графа на рисунке тензор бисмежности будет таким:
Мы привели явный вид данного тензора, чтобы показать, — нет особой необходимости трактовать преобразования на языке графов и матриц. В конечном счете все сводится к операциям реляционной алгебры.
Элементы множества, связи между которыми хотим определить, будем обозначать как (и ), а все множество как .
Для элементов дополнительного к нему множества (доли) используем символы (и ). Это могут быть документы, в которых сотрудники оставляют комментарии, или товарные накладные, если ищем связи между товарами.
Тензор связей (матрица бисмежности) между множествами считается заданным.
Для каждого объекта (вершины графа) можно определить его степень. Это количество связей данного объекта. Например, для документов степень — это количество ссылок на него (сколько в нем всего комментариев или товаров), для слова — его длина (количество букв). Степени дополнительной доли обозначим , значения степеней равны сумме по колонкам матрицы смежности :
Здесь — свертка тензора по измерению . Эквивалентна произведению матрицы на кортеж из единиц .
Формула преобразования
В общем случае элементы доли могут быть тоже связаны (на рисунке такие связи обозначены пунктиром). Учтем это введением матрицы связей (смежности) . Если граф двудольный, то данные связи (и их матрица) равны нулю.
Искомую матрицу результирующих связей между элементами множества (доли) обозначим как .
Тогда справедливо следующее утверждение (лемма):
Величина результирующих связей между элементами множества равна сумме исходных и наведенных связей:
При этом матрица наведенных связей представляет собой следующую квадратичную форму (это и есть основная формула статьи):
Здесь — фундаментальная матрица, которая определяется как обращение минора матрицы-лапласиана:
Все приведенные выше формулы пригодны для любого (неориентированного) графа, как двудольного, так и нет. Они вытекают из формул обращения блочных матриц.
Фишка двудольных графов заключается в том, что минор лапласиана для доли графа представляет собой диагональную матрицу, составленную из степеней элементов (поскольку нет связей между элементами). Поэтому обращение данного минора сводится просто к обратным значениям степеней :
В итоге вместо затратной процедуры обращения матрицы здесь имеем дело с обычным делением. Если речь идет о тысячах элементов, то данный нюанс имеет значение. Собственно ради его подчеркивания мы и написали данную статью.
Подставляя обратные степени в (3), получаем формулу преобразования матрицы би-смежности в матрицу смежности заданной доли:
Если тензор бисмежности задан в виде реляционной таблицы, то выполнить преобразование (6) можно одним sql-запросом. Ну а в библиотеках типа python pandas данное преобразование может быть записано одной строкой действий над объектом dataframe.
Пример расчета
Для приведенного выше тензора бисмежности степени элементов будут такими: . Соответственно, диагональ фундаментальной матрицы будет равна обратным значениям: . Подставляя ее в формулу (6), получаем тензор наведенных связей (для удобства приводим целочисленные значения):
На этом все. В следующей статье рассмотрим, для чего все это нужно, и какую полезную информацию можно извлечь из полученного подграфа.
Более подробная математика преобразования пространства графа в подпространство приведена здесь.

