- Раскрашиваем фрактал на основании глубины.
- Применяем случайную вариативность на основе последовательности.
- Добавляем листья с отличающимся внешним видом.
- Реализуем провисание фрактала под воздействием «гравитации».
- Добавляем вариативности для поворота и иногда меняем его направление.
В этом туториале мы изменим фрактал так, чтобы он выглядет более органически, нежели математически.
Туториал сделан в Unity 2019.4.18f1.

Модифицированный фрактал, выглядящий органическиим.
Градиент цвета
Фрактал, созданный нами в предыдущем туториале, очевидно, является результатом применения математики. Он выглядит строгим, точным, формальным и однородным. Он не выглядит ни органическим, ни живым. Однако внеся некоторые изменения, мы можем заставить математическое выглядеть в определнной степени органическим. Для этого мы внесём вариативность и случайность, а также симулируем поведение органики.
Наиболее простой способ повышения вариативности фрактала — это замена однородного цвета диапазоном цветов, и проще всего привязать его к уровню каждого отрисовываемого экземпляра.
Переопределяем цвет
Наш поверхностный DRP-шейдер имеет свойство _Color, которое мы пока настраиваем изменением материала, но можем переопределять в коде. Для этого будем отслеживать его идентификатор во
Fractal. static readonly int
colorId = Shader.PropertyToID("_Color"),
matricesId = Shader.PropertyToID("_Matrices");Затем вызовем
SetColor для блока свойства в цикле отрисовки внутри Update. Сначала мы зададим белый цвет, умноженный на текущее значение итератора цикла и разделённое на длину буфера минус один. При этом первый уровень станет чёрным, а последний — белым. for (int i = 0; i < matricesBuffers.Length; i++) {
ComputeBuffer buffer = matricesBuffers[i];
propertyBlock.SetColor(
colorId, Color.white * (i / (matricesBuffers.Length - 1))
);
propertyBlock.SetBuffer(matricesId, buffer);
Graphics.DrawMeshInstancedProcedural(
mesh, 0, material, bounds, buffer.count, propertyBlock
);
}Чтобы придать всем промежуточным уровням оттенки серого это должно быть деление с плавающей запятой, а не целочисленное, не имеющее дробной части. Мы можем обеспечить его, сделав вычитание единицы в делителе вычитанием с плавающей запятой. Остальная часть вычислений тоже станет вычислениями с плавающей запятой.
propertyBlock.SetColor(
colorId, Color.white * (i / (matricesBuffers.Length - 1f))
);Чтобы это работало в графе шейдера URP, нам нужно убедиться, что для albedo используется _Color. Внутреннее имя свойства отображается в графе шейдера как имя Reference свойства на blackboard.
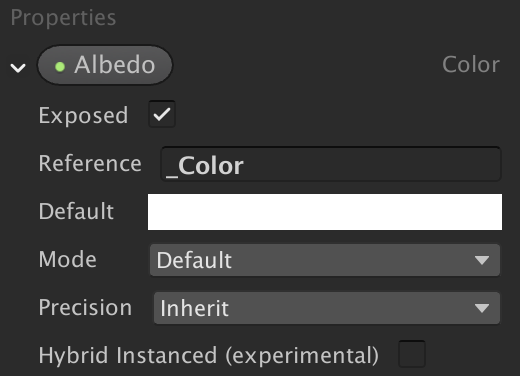
Внутреннее название Albedo — _Color.
В результате получается фрактал в градациях серого, идущий от чёрного цвета в корневом экземпляре до белого в экземплярах-листьях, как в DRP, так и в URP.

Фрактал в градиентных оттенках серого.
Обратите внимание, что вычитание единицы в делителе необходимо для получения белого на самом глубоком уровне. Но если глубина фрактала равна 1, то это приведёт к делению на ноль и к недопустимому цвету. Чтобы избежать этого, мы увеличим минимальную глубину до 2.
[SerializeField, Range(2, 8)]
int depth = 4;Интерполяция между цветами
Мы не ограничены только серыми или монохромными градиентами. Можно выполнять интерполяцию между двумя любыми цветами, вызывая статический метод
Color.Lerp с двумя цветами и коэффициентом, который мы ранее использовали в качестве интерполятора. Таким образом мы создадим в Update двухцветный градиент, например, от жёлтого к красному. propertyBlock.SetColor(
colorId, Color.Lerp(
Color.yellow, Color.red, i / (matricesBuffers.Length - 1f)
)
);
Фрактал в жёлто-красном градиенте.
Настраиваемый градиент
Мы можем сделать ещё один шаг и реализовать поддержку произвольных градиентов, имеющих больше двух настраиваемых цветов и неравномерное распределение. Это можно сделать при помощи типа
Gradient движка Unity. Используем его, чтобы добавить во Fractal настраиваемый градиент. [SerializeField]
Material material = default;
[SerializeField]
Gradient gradient = default;Свойство Gradient, которому заданы белый, красный и чёрный цвета.
Чтобы использовать градиент, заменим вызов
Color.Lerp в Update на вызов Evaluate градиента, снова с тем же значением интерполятора. propertyBlock.SetColor(
colorId, gradient.Evaluate(i / (matricesBuffers.Length - 1f))
);
Фрактал с настраиваемым бело-красно-чёрным градиентом.
Произвольные цвета
Раскрашенный градиентом фрактал выглядит интереснее, чем однородный, но заметно, что раскраска реализована по формуле. В органических объектах обычно присутствует некая вариативность цвета, кажущаяся случайной. В нашем случае это означает, что отдельные экземляры мешей должны демонстрировать вариативность цветов.
Функция цвета в шейдере
Чтобы одновременно выполнить работу и для поверхностного шейдера, и для графа шейдера, мы будем передавать цвет экземпляра через HLSL-файл FractalGPU. Начнём с объявления в нём поля свойства _Color, за которым следует функция
GetFractalColor, которая просто возвращает это поле. Разместим её над функциями графа шейдера.float4 _Color;
float4 GetFractalColor () {
return _Color;
}
void ShaderGraphFunction_float (float3 In, out float3 Out) {
Out = In;
}Затем удалим избыточное теперь свойство из поверхностного шейдера и вызовем
GetFractalColor внутри ConfigureSurface вместо прямого доступа к полю. //float4 _Color;
float _Smoothness;
void ConfigureSurface (Input input, inout SurfaceOutputStandard surface) {
surface.Albedo = GetFractalColor().rgb;
surface.Smoothness = _Smoothness;
}Мы больше не используем инспектор материалов для настройки albedo, поэтому можем удалить его из блока
Properties. Properties {
//_Color ("Albedo", Color) = (1.0, 1.0, 1.0, 1.0)
_Smoothness ("Smoothness", Range(0,1)) = 0.5
}Раскроем цвет фрактала нашему графу шейдера, добавив в функции графа выходной параметр, который мы для него создали.
void ShaderGraphFunction_float (float3 In, out float3 Out, out float4 FractalColor) {
Out = In;
FractalColor = GetFractalColor();
}
void ShaderGraphFunction_half (half3 In, out half3 Out, out half4 FractalColor) {
Out = In;
FractalColor = GetFractalColor();
}В самом графе шейдера мы сначала должны удалить свойство Albedo. Его можно удалить через контекстное меню, открытое правой клавишей мыши на её метке на blackboard.
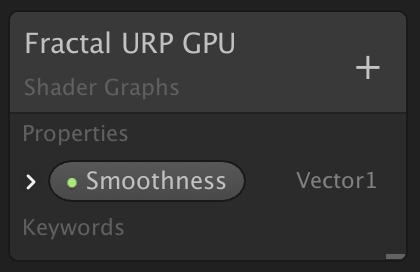
Осталось только свойство smoothness.
Затем добавим вывод к нашем ноду функции.
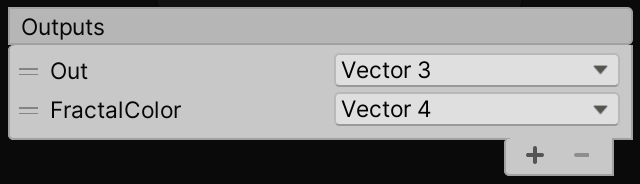
Дополнительный вывод FractalColor нашей функции.
И наконец соединим новый вывод с основным albedo.

Используем FractalColor в качестве albedo.
Привязываем цвет к идентификатору экземпляра
Чтобы добавить вариативность, зависящую от экземпляра, нам нужно каким-то образом привязать
GetFractalColor к идентификатору отрисовываемого экземпляра. Так как это целочисленное число, отсчёт которого ведётся с нуля, проще всего протестировать это можно, например, возвращая идентификатор экземпляра, уменьшенный на три порядка величин, что даст нам градиент в оттенках серого.float4 GetFractalColor () {
return unity_InstanceID * 0.001;
}Но теперь нам также нужно гарантировать, что мы выполняем доступ к идентификатору экземпляра только для вариантов шейдера, у которых включено процедурное создание экземпляров, как мы делали это в
ConfigureProcedural.float4 GetFractalColor () {
#if defined(UNITY_PROCEDURAL_INSTANCING_ENABLED)
return unity_InstanceID * 0.001;
#endif
}Разница в данном случае заключается в том, что нам всегда нужно что-то возвращать, даже несмотря на то, что это не имеет особого смысла. Поэтому мы просто будем возвращать для вариантов шейдера без создания экземпляров заданный цвет. Это реализуется вставкой директивы
#else перед #endif и возвратом между ними цвета. #if defined(UNITY_PROCEDURAL_INSTANCING_ENABLED)
return unity_InstanceID * 0.001;
#else
return _Color;
#endif
Раскраска по идентификатору экземпляра.
Это демонстрирует, что наше решение работает, хоть и выглядит ужасно. Мы можем сделать градиент более приятным, например, повторяя его через каждые пять экземпляров. Для этого мы используем остаток от деления идентификатора экземпляра на пять при помощи оператора
%. Это превращает ряд идентификаторов в повторяющуюся последовательность 0, 1, 2, 3, 4, 0, 1, 2, 3, 4,… Затем мы уменьшим их в четыре раза, чтобы интервал снизился с 0–4 до 0–1. return (unity_InstanceID % 5.0) / 4.0;
Раскраска делением с остатком на 5.
Получившаяся раскраска уже кажется на первый взгляд произвольной, даже несмотря на регулярную зацикленность градиента, потому что она не полностью совпадает с геометрической структурой фрактала. Заметный паттерн заключается в том, что центральный столбец всегда чёрный, потому что состоит из первого экземпляра каждого уровня. Это явление также проявляет себя на более глубоких уровнях, когда последовательность начинает совпадать с геометрией.
Мы можем изменить паттерн, меняя длину последовательности, например, увеличив её до десяти. Это добавляет больше вариативности и снижает повторяемость чёрных столбцов, хоть и выделяет их сильнее.
return (unity_InstanceID % 10.0) / 9.0;
Раскраска делением с остатком на 10.
Ряды Вейля
Немного иной способ создания повторяющегося градиента — это использование ряда Вейля. Если вкратце, то это ряды вида 0X поделить на 1 с остатком, 1X поделить на 1 с остатком, 2X поделить на 1 с остатком, 3X поделить на 1 с остатком, и так далее. Таким образом мы получаем только дробные значения из интервала 0–1, не включая 1. Если X — иррациональное число, то этот ряд будем равномерно распределён в данном интервале.
На самом деле нам не нужно идеальное распределение, только достаточная вариативность. В качестве X подойдёт случайное значение в интервале 0–1. Например, рассмотрим 0.381:
0.000, 0.381, 0.762, 0.143, 0.524, 0.905, 0.286, 0.667, 0.048, 0.429, 0.810, 0.191, 0.572, 0.953, 0.334, 0.715, 0.096, 0.477, 0.858, 0.239, 0.620, 0.001, 0.382, 0.763, 0.144, 0.525.
И мы получаем повторения почти трёхступенчатых, но иногда двухступенчатых возрастающих градиентов, каждый из которых немного отличается. Паттерн повторяется спустя 21 ступень, но со сдвигом на 0.001. При других значениях будут создаваться другие паттерны с другими градиентами, которые могут быть длиннее, короче или обратными.
В шейдере мы можем реализовать этот ряд простым умножением и передачей результата в функцию
frac. return frac(unity_InstanceID * 0.381);
Раскрашенный ряд, основанный на значении 0.381.
Случайный коэффициент и смещение
Результат использования дробного ряда выглядит приемлемо, но мы всё равно получаем эти чёрные столбцы. Можно избавиться от них, добавив к ряду различное смещение для каждого уровня, и даже использовать на каждом уровне свой ряд. Для этого добавим вектор свойства шейдера для двух чисел ряда, первое будет множителем, а второе смещением, а затем используем их в
GetFractalColor. Смещение должно прибавляться до изолирования дробной части значения, чтобы оно применило к ряду зацикленный сдвиг.float2 _SequenceNumbers;
float4 GetFractalColor () {
#if defined(UNITY_PROCEDURAL_INSTANCING_ENABLED)
return frac(unity_InstanceID * _SequenceNumbers.x + _SequenceNumbers.y);
#else
return _Color;
#endif
}Будем отслеживать идентификатор свойства шейдера в
Fractal. static readonly int
colorId = Shader.PropertyToID("_Color"),
matricesId = Shader.PropertyToID("_Matrices"),
sequenceNumbersId = Shader.PropertyToID("_SequenceNumbers");Затем добавим массив чисел ряда для каждого уровня, изначально приравненный к нашей текущей конфигурации, то есть к 0.381 и 0. Для этого мы используем тип
Vector4, потому что GPU можно передавать только четырёхкомпонентные векторы, даже если нам нужно меньше компонентов. Vector4[] sequenceNumbers;
void OnEnable () {
…
sequenceNumbers = new Vector4[depth];
int stride = 12 * 4;
for (int i = 0, length = 1; i < parts.Length; i++, length *= 5) {
…
sequenceNumbers[i] = new Vector4(0.381f, 0f);
}
…
}
void OnDisable () {
…
sequenceNumbers = null;
}Зададим число ряда для каждого уровня в цикле отрисовки в
Update, вызывая SetVector для блока свойств. propertyBlock.SetBuffer(matricesId, buffer);
propertyBlock.SetVector(sequenceNumbersId, sequenceNumbers[i]);Далее, чтобы сделать ряды произвольными и разными для каждого уровня, мы заменим постоянные заданные числа ряда случайными значениями. Для этого мы воспользуемся для этого
UnityEngine.Random, но этот тип конфликтует с Unity.Mathematics.Random, поэтому используем соответствующий тип явным образом.using quaternion = Unity.Mathematics.quaternion;
using Random = UnityEngine.Random;Затем для получения случайного значения просто заменим две константы на
Random.value, возвращающий значение в интервале 0–1. sequenceNumbers[i] = new Vector4(Random.value, Random.value);
Раскрашенные ряды со случайными коэффициентами и смещениями.
Два градиента
Чтобы скомбинировать случайный ряд с имеющимся градиентом, мы добавим второй градиент и будем передавать оба цвета GPU. Поэтому заменим одно свойство цвета свойствами для цветов A и B.
static readonly int
colorAId = Shader.PropertyToID("_ColorA"),
colorBId = Shader.PropertyToID("_ColorB"),
matricesId = Shader.PropertyToID("_Matrices"),
sequenceNumbersId = Shader.PropertyToID("_SequenceNumbers");Также заменим один настраиваемый градиент градиентами A и B.
[SerializeField]
Gradient gradientA = default, gradientB = default;Затем вычислим оба градиента в цикле отрисовки
Update и зададим их цвета. float gradientInterpolator = i / (matricesBuffers.Length - 1f);
propertyBlock.SetColor(colorAId, gradientA.Evaluate(gradientInterpolator));
propertyBlock.SetColor(colorBId, gradientB.Evaluate(gradientInterpolator));
Свойства двух градиентов.
Также заменим свойство одного цвета в FractalGPU на два.
//float4 _Color;
float4 _ColorA, _ColorB;И выполним интерполяцию между ними в
GetFractalColor при помощи lerp, взяв в качестве интерполятора результат ряда. return lerp(
_ColorA, _ColorB,
frac(unity_InstanceID * _SequenceNumbers.x + _SequenceNumbers.y)
);Для случая
#else просто будем возвращать цвет A. #else
return _ColorA;
#endif
Раскраска двумя градиентами.
Обратите внимание, что результат является не двоичным выбором из двух цветов на экземпляр, а смешением.
Листья
Распространённая особенность растений заключается в том, что их конечные части специализированы. Примерами этого являются листья, цветы и фрукты. Мы можем добавить эту особенность в наш фрактал, сделав самый глубокий уровень отличающимся от остальных. Теперь мы будем считать его уровнем листьев, хоть он и не представляет собой настоящие листья.
Цвета листьев
Чтобы сделать экземпляры-листья нашего фрактала отличающимися, мы придадим им другой цвет. Хоть мы и можем сделать это просто через градиент, удобнее будет настраивать цвет листа отдельно, оставив градиенты для ствола, ветвей и побегов. Поэтому добавим во
Fractal опции конфигурации для двух цветов листьев. [SerializeField]
Gradient gradientA = default, gradientB = default;
[SerializeField]
Color leafColorA = default, leafColorB = default;
Свойства цветов листьев.
В
Update определим перед циклом отрисовки индекс листа, который равен последнему индексу. int leafIndex = matricesBuffers.Length - 1;
for (int i = 0; i < matricesBuffers.Length; i++) { … }Затем внутри цикла непосредственно используем настроенные для уровня листьев цвета, и вычислим градиенты для всех остальных уровней. Кроме того, поскольку теперь мы завершаем градиент на один шаг раньше, то при вычислении интерполятора вычитаем из длины буфера не 1, а 2.
Color colorA, colorB;
if (i == leafIndex) {
colorA = leafColorA;
colorB = leafColorB;
}
else {
float gradientInterpolator = i / (matricesBuffers.Length - 2f);
colorA = gradientA.Evaluate(gradientInterpolator);
colorB = gradientB.Evaluate(gradientInterpolator);
}
propertyBlock.SetColor(colorAId, colorA);
propertyBlock.SetColor(colorBId, colorB);
Фрактал с отличающимися цветами листьев.
Обратите внимание, что это изменение заставляет нас ещё больше инкрементировать минимальную глубину фрактала.
[SerializeField, Range(3, 8)]
int depth = 4;Меш листа
Теперь мы обрабатываем самый нижний уровень отдельно, поэтому для его отрисовки можем использовать и другой меш. Добавим для этого поле конфигурации. Благодаря этому в качестве листьев можно использовать куб, ведь для всего остального мы используем сферы.
[SerializeField]
Mesh mesh = default, leafMesh = default;Свойству меша листа задан куб.
Используем соответствующий меш при вызове
Graphics.DrawMeshInstancedProcedural в Update. Mesh instanceMesh;
if (i == leafIndex) {
colorA = leafColorA;
colorB = leafColorB;
instanceMesh = leafMesh;
}
else {
float gradientInterpolator = i / (matricesBuffers.Length - 2f);
colorA = gradientA.Evaluate(gradientInterpolator);
colorB = gradientB.Evaluate(gradientInterpolator);
instanceMesh = mesh;
}
…
Graphics.DrawMeshInstancedProcedural(
instanceMesh, 0, material, bounds, buffer.count, propertyBlock
);
Кубы в качестве листьев.
Кроме того, что это выглядит интереснее, использование кубов в качестве листьев значительно повышает производительность, потому что большинство экземпляров теперь является кубами.
| Глубина | URP | DRP |
|---|---|---|
| 6 | 430 | 142 |
| 7 | 140 | 91 |
| 8 | 49 | 31 |
Smoothness
Кроме отличающегося цвета мы также можем придать листьям другую шероховатость (smoothness). На самом деле, мы можем варьировать smoothness так же, как варьируем цвет, на основании второго ряда. Чтобы настроить этот второй ряд нам достаточно заполнить в
OnEnable два оставшихся компонента вектора чисел ряда случайными значениями. sequenceNumbers[i] = new Vector4(
Random.value, Random.value, Random.value, Random.value
);Затем мы по отдельности интерполируем каналы RGB и A в
GetFractalColor на основании двух других заданных чисел для канала A.float4 _SequenceNumbers;
float4 GetFractalColor () {
#if defined(UNITY_PROCEDURAL_INSTANCING_ENABLED)
float4 color;
color.rgb = lerp(
_ColorA.rgb, _ColorB.rgb,
frac(unity_InstanceID * _SequenceNumbers.x + _SequenceNumbers.y)
);
color.a = lerp(
_ColorA.a, _ColorB.a,
frac(unity_InstanceID * _SequenceNumbers.z + _SequenceNumbers.w)
);
return color;
#else
return _Color;
#endif
}Мы делаем так, потому что теперь будем использовать канал A цвета для задания smoothness, что возможно благодаря тому, что мы не используем его для прозрачности. Это значит, что в нашем графе шейдера мы используем нод Split для извлечения альфа-канала из FractalColor и привязки его к основной smoothness. Затем удалим свойство smoothness из blackboard.
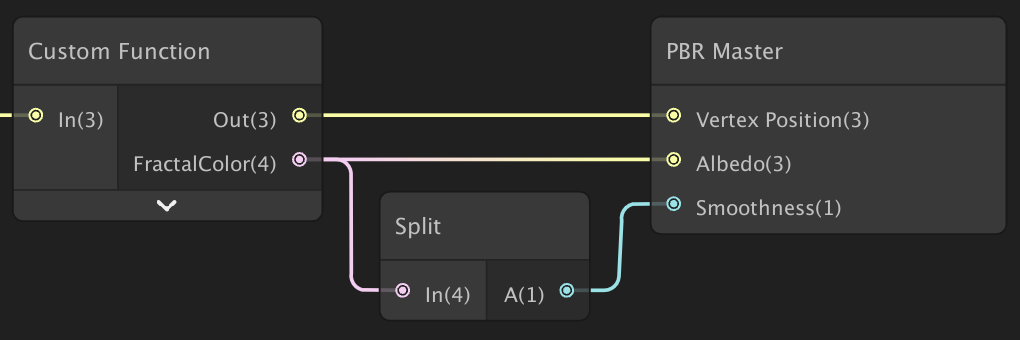
Полученная smoothness.
То же самое мы делаем в нашем поверхностном шейдере.
void ConfigureSurface (Input input, inout SurfaceOutputStandard surface) {
surface.Albedo = GetFractalColor().rgb;
surface.Smoothness = GetFractalColor().a;
}
Не должны ли мы повторно использовать результат одного вызова GetFractalColor?
Да, но мы уже и так делаем это. Компилятор шейдера распознаёт и оптимизирует дублируемую работу. Стоит заметить, что это всегда происходит в случае шейдеров, но обычно не происходит в обычном коде на C#.
Теперь мы можем удалить из поверхностного шейдера весь блок
Properties. //Properties {
//_Smoothness ("Smoothness", Range(0,1)) = 0.5
//}Так как теперь мы можем использовать альфа-канал цвета для управления smoothness, нужно настроить цвета, чтобы учитывать это. Например, я задал smoothness листа равной 50% и 90%. Обратите внимание, что smoothness выбирается вне зависимости от цвета, хотя они вместе настраиваются через одно свойство. Мы просто пользуемся уже существующим каналом, который пока не использовался.
Чёрные листья с варьируемой smoothness.
Тоже самое нужно проделать и с градиентами, для которых по умолчанию установлено 100% альфы. Я задал им 80–90 и 140–160 из 255. Также я настроил цвета, чтобы фрактал больше походил на дерево.


Фрактал раскрашен так, чтобы напоминать растение.
Эффект наиболее реалистичен, когда глубина фрактала установлена на максимум.

Та же раскраска с глубиной 8.
Провисание ветвей
Хотя наш фрактал уже выглядит намного органичнее, это относится только к его раскраске. Его структура по-прежнему жёсткая и идеальная. Проще всего увидеть это со стороны, когда окно сцены находится в ортографическом режиме, а вращение в
Update временно установлено на ноль. float spinAngleDelta = 0.125f * PI * Time.deltaTime * 0f;
Идеально жёсткая структура.
Органические структуры неидеальны. Кроме того, что они неравномерно добавляются в процессе роста, наиболее очевидным качеством растений является то, что они подвержены воздействию гравитации. Всё в растении хотя бы немного провисает под собственным весом. В нашем фрактале этого нет, но мы можем аппроксимировать это явление, изменив поворот каждой части.
Ось поворота провисания
Мы можем симулировать провисание, повернув всё так, чтобы элементы немного наклонились вниз. То есть нам нужно повернуть каждый экземпляр вокруг какой-то оси, чтобы локальная ось вверх казалась опущенной вниз. Значит, первым делом нам нужно определить направленную вверх ось элемента в мировом пространстве. Это ось, которая указывает в направлении, противоположном родительскому элементу. Мы найдём её, повернув вектор вверх на изначальный поворот элемента в мире. Это надо выполнять без учёта собственного предыдущего провисания элемента, в противном случае поворот будет накапливаться и всё достаточно быстро станет направленным ровно вниз. Поэтому мы выполняем поворот в начале
Execute на основании фиксированного локального поворота элемента и поворота его родителя в мировом пространстве, прежде чем изменять поворот элемента в мире. public void Execute (int i) {
FractalPart parent = parents[i / 5];
FractalPart part = parts[i];
part.spinAngle += spinAngleDelta;
float3 upAxis =
mul(mul(parent.worldRotation, part.rotation), up());
part.worldRotation = mul(parent.worldRotation,
mul(part.rotation, quaternion.RotateY(part.spinAngle))
);
…
}Если элемент не направлен прямо вверх, то его собственная ось вверх будет отличаться от оси вверх мира. Можно выполнить поворот от мировой оси вверх к оси вверх элемента, осуществив поворот вокруг ещё одной оси. Эту ось, которую мы назовём осью провисания, можно найти, взяв векторное произведение обоих осей при помощи метода
cross. float3 upAxis =
mul(mul(parent.worldRotation, part.rotation), up());
float3 sagAxis = cross(up(), upAxis);Результатом векторного произведения является вектор, перпендикулярный обоим его аргументам. Длина вектора зависит от относительной ориентации и длин исходных векторов. Так как мы работаем с единичными веторами, длина оси провисания равна синусу угла между операндами. Поэтому чтобы прийти к оси единичной длины, нам нужно отмасштабировать её до единичной длины, для чего можно воспользоваться методом
normalize. float3 sagAxis = cross(up(), upAxis);
sagAxis = normalize(sagAxis);Применяем провисание
Теперь, когда у нас есть ось провисания, мы можем создать поворот провисания, вызвав
quaternion.AxisAngle с осью и углом в радианах. Давайте создадим поворот на 45°, то есть на четверть ? радиан. sagAxis = normalize(sagAxis);
quaternion sagRotation = quaternion.AxisAngle(sagAxis, PI * 0.25f);Чтобы применить провисание, нам нужно базировать поворот элемента в мире не напрямую на повороте родителя. Мы введём поворот по новому основанию, применив поворот провисания к повороту родительского элемента в мире.
quaternion sagRotation = quaternion.AxisAngle(sagAxis, PI * 0.25f);
quaternion baseRotation = mul(sagRotation, parent.worldRotation);
part.worldRotation = mul(baseRotation,
mul(part.rotation, quaternion.RotateY(part.spinAngle))
);
Верхушка отсутствует.
Разница очевидна, но результат неверный. Наиболее важная ошибка заключается в том, что вершина фрактала как будто отсутствует. Так получилось, потому что когда элемент направлен ровно вверх, угол ним и мировой осью вверх равен нулю. Поэтому результат векторного произведения равен вектору нулевой длины, для которого нормализацию выполнить не удаётся. Мы исправим эту ошибку проверкой того, больше ли нуля величина вектора провисания (его длина). Если это так, то применяем провисание, а в противном случае напрямую применяем поворот родительского элемента. Это логично с точки зрения физики, потому что если элемент направлен вверх, то находится в равновесии и не будет провисать.
Длину вектора, также известную как его величина, можно найти с помощью метода
length. После этого вектору можно придать единичную длину, разделив его на его величину, что и делает normalize. //sagAxis = normalize(sagAxis);
float sagMagnitude = length(sagAxis);
quaternion baseRotation;
if (sagMagnitude > 0f) {
sagAxis /= sagMagnitude;
quaternion sagRotation = quaternion.AxisAngle(sagAxis, PI * 0.25f);
baseRotation = mul(sagRotation, parent.worldRotation);
}
else {
baseRotation = parent.worldRotation;
}
part.worldRotation = mul(baseRotation,
mul(part.rotation, quaternion.RotateY(part.spinAngle))
);
Вершина есть, но деформированная.
Фрактал всё равно деформирован, потом что теперь мы по сути применяем ориентацию каждого элемента дважды. Сначала при провисании и позже, когда смещаем при использовании провисания, а потом когда смещаем его в определённом направлении. Исправим это, всегда выполняя смещение вдоль локальной оси вверх элемента.
part.worldPosition =
parent.worldPosition +
//mul(parent.worldRotation, (1.5f * scale * part.direction));
mul(part.worldRotation, float3(0f, 1.5f * scale, 0f));
Равномерное провисание на 45°.
Обратите внимание — это значит, что нам больше не надо отслеживать вектор направления каждой части и мы можем удалить весь связанный с ним код.
struct FractalPart {
//public float3 direction, worldPosition;
public float3 worldPosition;
public quaternion rotation, worldRotation;
public float spinAngle;
}
…
//static float3[] directions = {
// up(), right(), left(), forward(), back()
//};
…
FractalPart CreatePart (int childIndex) {
return new FractalPart {
//direction = directions[childIndex],
rotation = rotations[childIndex]
};
}Модулированное провисание
Похоже, провисание работает, но важно наблюдать его, когда фрактал в движении, поэтому заставим его снова вращаться.
float spinAngleDelta = 0.125f * PI * Time.deltaTime; // * 0f;Исправленное провисание.
В целом это работает. Какой бы ни была ориентация элемента, кажется, что его тянет вниз. Но возникают случайные изменения направления. Это происходит, когда меняется направление провисания. Так как мы используем постоянный угол провисания, единственные варианты — провисать в положительном или отрицательном направлении, или не провисать совсем. Также это означает, что поворот распространяется на элементы, направленные почти прямо вниз, поднимая их вместо этого вверх.
Чтобы решить эту проблему, нужно сделать так, чтобы величина провисания зависела от угла между осью вверх мира и элемента. Если элемент направлен почти ровно вверх или вниз, то провисания почти не должно быть, а если элемент направлен в сторону под углом 90°, то провисание должно быть максимальным. Соотношение между величиной провисания и углом не должно быть линейным. На самом деле, хорошие результаты даёт синус угла. Это величина векторного произведения, которая у нас уже есть. Поэтому используем её для модуляции угла поворота провисания.
quaternion sagRotation =
quaternion.AxisAngle(sagAxis, PI * 0.25f * sagMagnitude);Модулированное провисание.
Так как провисание вычисляется в мировом пространстве, на него влияет ориентация всего фрактала. Поэтому немного повернув game object фрактала, мы можем заставить провисать и верхушку.
Фрактал, повёрнутый на 20° по оси Z.
Максимальный угол провисания
Теперь, когда провисание работает, сделаем его максимальный угол настраиваемым, снова добавив вариативности, раскрыв два значения для задания интервала. Для настройки этих углов мы воспользуемся градусами, потому что это легче, чем использовать радианы.
[SerializeField]
Color leafColorA = default, leafColorB = default;
[SerializeField, Range(0f, 90f)]
float maxSagAngleA = 15f, maxSagAngleB = 25f;
Максимальные углы провисания.
Добавим максимальный угол провисания в
FractalPart и инициализируем его в CreatePart вызовом Random.Range с двумя заданными углами в качестве аргументов. Результат можно преобразовать в радианы с помощью метода radians. struct FractalPart {
public float3 worldPosition;
public quaternion rotation, worldRotation;
public float maxSagAngle, spingAngle;
}
…
FractalPart CreatePart (int childIndex) {
return new FractalPart {
maxSagAngle = radians(Random.Range€(maxSagAngleA, maxSagAngleB)),
rotation = rotations[childIndex]
};
}
Обязательно ли угол A должен быть меньше угла B?
Хоть это и логично, но необязательно. Метод
Random.Range просто использует случайное значение для интерполяции между двумя его аргументами.Затем используем в
Execute максимальный угол провисания элемента вместо постоянных 45°. quaternion sagRotation =
quaternion.AxisAngle(sagAxis, part.maxSagAngle * sagMagnitude)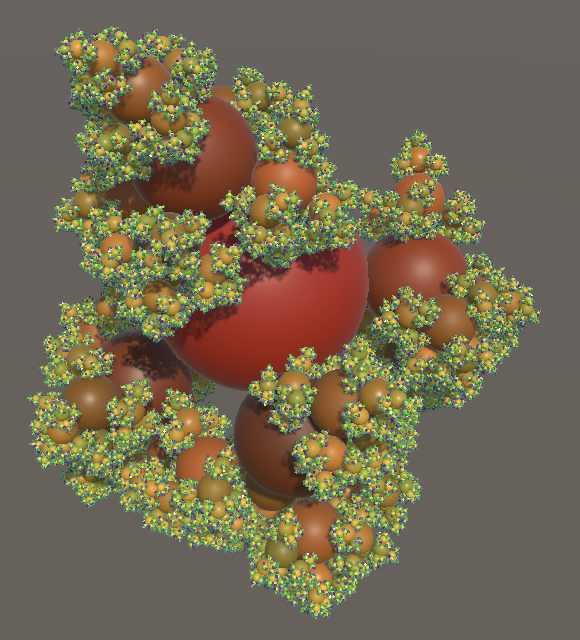
Переменный максимальный угол провисания 15–25, глубина 8.
Вращение
Мы уже модифицировали наш фрактал так, что он выглядит достаточно органическим. Последним усовершенствованием будет добавление вариативности вращению.
Переменная скорость
Как и в случае с максимальным углом провисания, добавим опции конфигурации для интервала скоростей вращения, задаваемых в градусах в секунду. Эти скорости должны быть равными или больше нуля.
[SerializeField, Range(0f, 90f)]
float maxSagAngleA = 15f, maxSagAngleB = 25f;
[SerializeField, Range(0f, 90f)]
float spinVelocityA = 20f, spinVelocityB = 25f;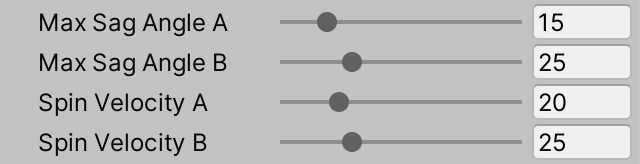
Скорости вращения.
Добавим в
FractalPart поле скорости вращения и случайным образом инициализируем его в CreatePart. struct FractalPart {
public float3 worldPosition;
public quaternion rotation, worldRotation;
public float maxSagAngle, spinAngle, spinVelocity;
}
…
FractalPart CreatePart (int childIndex) {
return new FractalPart {
maxSagAngle = radians(Random.Range€(maxSagAngleA, maxSagAngleB)),
rotation = rotations[childIndex],
spinVelocity = radians(Random.Range€(spinVelocityA, spinVelocityB))
};
}Затем избавимся от поля однородной дельты угла вращения в
UpdateFractalLevelJob, заменив её полем дельты времени. Затем применим собственную скорость вращения элемента в Execute. //public float spinAngleDelta;
public float scale;
public float deltaTime;
…
public void Execute (int i) {
FractalPart parent = parents[i / 5];
FractalPart part = parts[i];
part.spinAngle += part.spinVelocity * deltaTime;
…
}После этого изменим
Update так, чтобы в нём больше не использовалась однородная дельта угла вращения и вместо неё передавалась дельта времени. //float spinAngleDelta = 0.125f * PI * Time.deltaTime;
float deltaTime = Time.deltaTime;
FractalPart rootPart = parts[0][0];
rootPart.spinAngle += rootPart.spinVelocity * deltaTime;
…
for (int li = 1; li < parts.Length; li++) {
scale *= 0.5f;
jobHandle = new UpdateFractalLevelJob {
//spinAngleDelta = spinAngleDelta,
deltaTime = deltaTime,
…
}.ScheduleParallel(parts[li].Length, 5, jobHandle);
}Изменяемая в интервале от 0 до 90 скорость вращения.
Обратное вращение
Дополнительно мы можем реализовать смену направления вращения некоторых элементов. Это можно сделать, добавив возможность отрицательных скоростей вращения. Однако если мы захотим использовать и положительные, и отрицательные скорости, то два сконфигурированных значения должны будут иметь разные знаки. Следовательно, интервал будет проходить через ноль и невозможно будет избежать низких скоростей. Нельзя будет настроить фрактал так, чтобы его скорость, например, находилась в интервале 20–25, но с положительным или отрицательным знаком.
Решение заключается в отдельном задании скорости и направления. Для начала переименуем velocity в speed, чтобы обозначить, что скорость не имеет направления. Затем добавим ещё одну опцию конфигурации для вероятности обратного вращения, выраженного в виде вероятности, то есть значение будет находиться в интервале 0–1.
[SerializeField, Range(0f, 90f)]
float spinSpeedA = 20f, spinSpeedB = 25f;
[SerializeField, Range(0f, 1f)]
float reverseSpinChance = 0.25f;
…
FractalPart CreatePart (int childIndex) {
return new FractalPart {
maxSagAngle = radians(Random.Range(maxSagAngleA, maxSagAngleB)),
rotation = rotations[childIndex],
spinVelocity = radians(Random.Range(spinSpeedA, spinSpeedB))
};
}
Скорости и вероятность обратного вращения.
Мы можем выбирать направление вращения в
CreatePart, проверяя, меньше ли случайное значение вероятности обратного вращения. Если это так, то мы умножаем скорость на ?1, в противном случае на 1. spinVelocity =
(Random.value < reverseSpinChance ? -1f : 1f) *
radians(Random.Range(spinSpeedA, spinSpeedB))Разные направления вращения, скорость всегда равна 45°.
Обратите внимание, что теперь элементы фрактала могут казаться относительно неподвижными. Это происходит, когда противоположные скорости вращения обнуляют друг друга.
Производительность
Завершим мы снова изучением производительности после внесённых нами изменений. Похоже, время update увеличилось, приблизительно удвоившись для глубин 6 и 7, и увеличившись на 30% для глубины 8. Это не повлияло отрицательно на частоту кадров по сравнению с тем, когда мы измеряли её в последний раз.
| Глубина | MS | URP | DRP |
|---|---|---|---|
| 6 | 0.20 | 440 | 142 |
| 7 | 0.45 | 144 | 92 |
| 8 | 2.23 | 49 | 31 |

