28.05.2021 10:58
Shapelez 12 3500 Источник
Подсчёт количества элементов в потоке ограниченными средствами в представлении художника
Подсчёт количества элементов в потоке ограниченными средствами в представлении художника

Мы рады представить вашему вниманию заметку, написанную инженером Qrator Labs Дмитрием @dimak24 Камальдиновым. Если вы хотите быть частью нашей команды Core и заниматься подобными задачами — пишите нам на hr@qrator.net.

1 Введение

При реализации потоковых алгоритмов часто возникает задача подсчёта каких-то событий: приход пакета, установка соединения; при этом доступная память может стать узким местом: обычный n-битный счётчик позволяет учесть не более 2^n - 1событий. Одним из способов обработки большего диапазона значений, используя то же количество памяти, является вероятностный подсчёт. В этой статье будет предложен обзор известного алгоритма Морриса, а также некоторых его обобщений.

Другой способ уменьшить количество бит, необходимое для хранения значения счётчика, — использование распада. Об этом подходе мы рассказываем здесь, а также собираемся в ближайшее время опубликовать ещё одну заметку по теме.

Мы начнём с разбора простейшего алгоритма вероятностного подсчёта, выделим его недостатки (раздел 2). Затем (раздел 3) опишем алгоритм, впервые преложенный Робертом Моррисом в 1978 году, укажем его важнейшие свойства и приемущества. Для большинства нетривиальных формул и утверждений в тексте присутствуют наши доказательства — интересующийся читатель сможет найти их под спойлером. В трёх последующих разделах мы изложим полезные расширения классического алгоритма: вы узнаете, что общего у счётчиков Морриса и экспоненциального распада, как можно уменьшить ошибку, пожертвовав максимальным значением, и как эффективно обрабатывать взвешенные события.

2 Вероятностный подсчёт, проблемы тривиального подхода

Основная идея вероятностного подсчёта — учёт очередного события с некоторой вероятностью. Рассмотрим сначала пример с постоянной вероятностью обновления:

\begin{equation*} C_{n+1} = \left\{\begin{array}{ll} C_n + 1 & \textit{с вероятностью $p = const$} \\ C_n & \textit{с вероятностью $1-p$.} \end{array}\right. \end{equation*}

Где через C_nобозначено значение счётчика после n-ой попытки обновления. Несложно понять, что C_nзадаёт количество успехов среди nнезависимых испытаний Бернулли. Иначе говоря, C_nимеет биномиальное распределение:

\begin{align*} C_n \sim Bin(&n, p) \\ {\sf E} C_n = &np \\ {\sf D} C_n = &np(1-p). \end{align*}

В качестве оценки числа событий nестественно использовать \widehat{n}(C) := C/p. Ясно, что такая оценка несмещённая: {\sf E}\widehat{n}(C_n) = ({\sf E}C_n)/p = np/p = n.

Описанный подход имеет несколько недостатков: во-первых, он позволяет учесть лишь в 1/p = constраз больше событий по сравнению с простым инкрементальным счётчиком, чем заметно уступает счётчикам Морриса, как мы увидим далее. Во-вторых, относительная ошибка оценки велика при маленьких n. Например, при n=1она вообще равна 100%. Оценить относительную ошибку можно с помощью коэффициента вариации:

\begin{align*} {\sf CV}\widehat{n}(C_n) = \frac{\sqrt{{\sf D}\widehat{n}(C_n)}}{{\sf E} \widehat{n}(C_n)} = \sqrt{\frac{1-p}{pn}}. \end{align*}

3 Счётчики Морриса

Счётчик Морриса обновляется с вероятностью, зависящей от текущего значения: первое обновление происходит с вероятностью 1, следующее с вероятностью 1/2, потом 1/4 и т.д.:

\begin{equation*} C_{n+1} = \left\{\begin{array}{ll} C_n + 1 & \textit{с вероятностью $2^{-C_n}$} \\ C_n & \textit{с вероятностью $1 - 2^{-C_n}$.} \end{array}\right. \end{equation*}

Как по значению счётчика оценить, сколько было событий? Обновление счётчика с xна x + 1происходит в среднем за 2^xитераций, отсюда оценка числа событий:

\widehat{n}(C) := \sum_{i=0}^{C-1} 2^{i} = 2^C - 1.

Важнейшими свойствами этой оценки являются

  • её несмещённость, то есть значение оценки после nвероятностных обновлений в среднем равно n,

Доказательство
\begin{align*} {\sf E}\left(2^{C_n} | C_{n-1} = y\right) =& \underbrace{2^{y + 1} 2^{-y}}_{\textit{счётчик обновился}} + \underbrace{2^y (1 - 2^{-y})}_{\textit{значение не изменилось}} = 2^y + 1 \implies \\ {\sf E}\left(2^{C_n}|C_{n-1}\right) =& 2^{C_{n-1}} + 1 \implies {\sf E}2^{C_n} = {\sf E}2^{C_{n-1}} + 1 = {\sf E}2^{C_{n-2}} + 2 = \dots \end{align*}

В самом начале значение счётчика равно 0: C_0 = 0, тогда {\sf E}2^{C_0} = 2^{0} = 1, а значит {\sf E} 2^{C_n} = \dots = n + 1. Итого {\sf E}\widehat{n}(C_n) = {\sf E}2^{C_n} - 1 = n.

  • а также независимость её относительной ошибки от n.

Доказательство

Сначала посчитаем дисперсию \widehat{n}(C_n). Согласно известной формуле, {\sf D}\widehat{n} = {\sf E}\widehat{n}^2 - ({\sf E}\widehat{n})^2. Мы уже знаем, что {\sf E}\widehat{n}(C_n) = n. Осталось получить {\sf E}\widehat{n}(C_n)^2. Заметим, что

\begin{align*} {\sf E}\left(2^{C_n} - 1\right)^2 = {\sf E}2^{2C_n} - 2(n+1) + 1 = {\sf E}2^{2C_n} - 2n - 1. \end{align*}

Таким образом, остаётся узнать, чему равно {\sf E}2^{2C_n}.

\begin{align*} {\sf E}\left(2^{2C_n} | C_{n-1} = y\right) &= \underbrace{2^{2(y + 1)} 2^{-y}}_{\textit{счётчик обновился}} + \underbrace{2^{2y}(1 - 2^{-y})}_{\textit{значение не изменилось}} = \\ 3 \cdot 2^y +2^{2y} &\implies {\sf E}\left(2^{2C_n} | C_{n-1}\right) = 3 \cdot 2^{C_{n-1}} + 2^{2C_{n-1}} \implies \\ {\sf E} 2^{2C_n} = 3n &+ {\sf E}2^{2C_{n-1}} = 3n + 3(n-1) + {\sf E}2^{2C_{n-2}} = \dots = \sum_{i=1}^n 3i \end{align*}

Итого

\begin{equation*} {\sf D}\widehat{n}(C_n) = \frac{3n(n+1)}{2} - 2n - 1 - n^2 = \frac{n^2 - n - 2}{2} \end{equation*}\begin{equation*} {\sf CV}\widehat{n}(C_n) = \frac{\sqrt{{\sf D}\widehat{n}(C_n)}}{{\sf E}\widehat{n}(C_n)} = \sqrt{\frac{n^2-n-2}{2n^2}} \sim \frac{1}{\sqrt{2}}. \end{equation*}

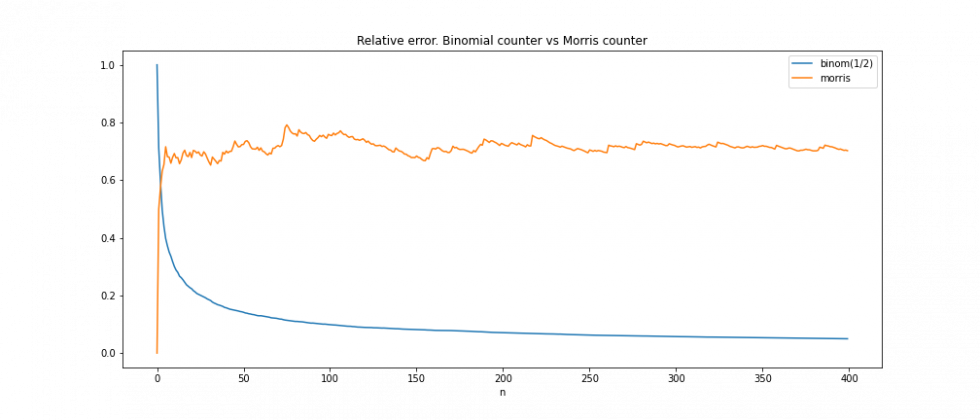
Таким образом, относительная ошибка оценки числа событий при использовании счётчика Морриса ограничена, примерно постоянна и почти не зависит от n.

Оценить вероятность больших отклонений от среднего можно с помощью неравенства Чебышёва:

\begin{align*} {\sf P}(|\widehat{n}(C_n) - n| \ge \varepsilon n) \le \frac{{\sf D}\widehat{n}(C_n)}{\varepsilon^2n^2} \sim \frac{1}{2\varepsilon^2}. \end{align*}

  • отметим здесь также, что покрываемый диапазон количества событий при использовании {\bf X}бит памяти будет 2^{2^{\bf X}} - 1. Иначе говоря, для учёта nсобытий достаточно \mathcal{O}(\log \log n)бит памяти!

Рис. 1: Относительная ошибка оценки числа событий при использовании биномиальных счётчиков и счётчиков Морриса (для построения графика sample_size=100 раз запускался процесс обновления счётчика, затем каждой точке n сопоставлялось среднее значение по этой выборке относительной ошибки после n обновлений)
Рис. 1: Относительная ошибка оценки числа событий при использовании биномиальных счётчиков и счётчиков Морриса (для построения графика sample_size=100 раз запускался процесс обновления счётчика, затем каждой точке n сопоставлялось среднее значение по этой выборке относительной ошибки после n обновлений)

4 Взвешенные обновления

Счётчики Морриса можно использовать для подсчёта взвешенных событий: например, для суммирования размеров приходящих пакетов. Простейший способ — обновление счётчика <вес события> раз — приводит к линейной по весу сложности обновления.

Заметим, что в каждый момент времени мы знаем, как распределено количество неудач до ближайшего изменения счётчика, — это геометрическое рапределение:

\begin{align*} {\sf P}(n_{fail} = k) = (1 - 2^{-C})^k 2^{-C} \implies n_{fail} \sim Geom(2^{-C}). \end{align*}

Учитывая этот факт, мы можем ускорить алгоритм, сразу пропуская все подряд идущие неудачные попытки обновления:

5 Распад

Часто возникает потребность учитывать самые новые события с большим весом. Например, при поиске интенсивных ключей в потоке интереснее понять, какой ключ интенсивен прямо сейчас, а не имеет высокую среднюю интенсивность за счёт своего бурного прошлого. В статье мы рассказывали о распадных счётчиках, спроектированных специально для решения этой задачи. Другой предпосылкой для некоего распада является то, что несмотря на суперэкономное использование памяти, когда-то и счётчик Морриса переполнится. Оказывается, счётчики Морриса тоже могут распадаться, причём очень похожим на EMA способом, но гораздо эффективнее.

Идея очень проста: будем периодически вычитать 1из счётчика. Напомним, что значение Cоценивает количество событий как

\sum_{i=0}^{C-1} 2^i = 2^C - 1 =: n_0.

Соответственно, после вычитания 1оценка станет2^{C-1} - 1 = \frac{1}{2}n_0 - \frac{1}{2}. Иначе говоря, вычитание 1уменьшает оценку в \sim 2раза! Мы можем добиться распада ровно в 2раза, обновив с вероятностью \frac{1}{2}счётчик сразу после вычитания 1:

6 Мантисса и экспонента

Рассмотрим следующее обобщение счётчика Морриса: вероятность обновления уменьшается в 2раза не на каждое успешное обновление, а на каждые {\bf X}. Возможной реализацией такого подхода будет разделение битов счётчика на две части: экспоненту, отвечающую за вероятность, и мантиссу, считающую количество успешных обновлений при текущей вероятности (чем-то похоже на представление чисел с плавающей точкой).

Рис. 2: разбиение битов счётчика на мантиссу (M=5 бит) и экспоненту (E=3 бит)
Рис. 2: разбиение битов счётчика на мантиссу (M=5 бит) и экспоненту (E=3 бит)

Введём обозначения для мантиссы и экспоненты:

\begin{align*} {\rm e}(C) &= C \gg {\bf M} \\ {\rm m}(C) &= C \& (2^{\bf M} - 1). \end{align*}

Теперь правило обновления и оценка числа событий записываются так:

\begin{align*} C_{n+1} &= \left\{\begin{array}{ll} C_n + 1, & \textit{с вероятностью $2^{-{\rm e}(C)}$} \\ C_n, & \textit{с вероятностью $1 - 2^{-{\rm e}(C)}$} \end{array}\right. \\ \widehat{n}(C) &= (2^{{\rm e}(C)} - 1)2^{\bf M} + 2^{{\rm e}(C)}{\rm m}(C). \end{align*}

Например, на рисунке 2 значение счётчика C = 89, мантисса и экспонента равны {\rm m} = 25и {\rm e} = 2соответственно. А значит число событий оценивается как \widehat{n} = (2^2 - 1) \times 2^5 + 2^2 \times 25 = 196.

При таком разбиении биты экспоненты будут отвечать за покрываемый диапазон количества событий, а биты мантиссы за точность оценки (далее мы поясним подробнее, что это значит). Наилучшее распределение битов счётчика зависит от задачи; мы предлагаем отдавать как можно больше мантиссе, но чтобы экспоненциальных битов хватало для покрытия интересующего диапазона значений.

Описанный вариант счётчиков Морриса обладает следующими свойствами:

  • покрываемый диапазон значений равен

\begin{align*} {\bf N}_{max} = 2^{2^{\bf E} + {\bf M}} - \left(2^{2^{\bf E} - 1} + 2^{\bf M}\right); \end{align*}
Доказательство

Покрываемый диапазон получить несложно, подставив в формулу для \widehat{n}максимальные возможные значения {\rm m} = 2^{\bf M} - 1и {\rm e} = 2^{\bf E} - 1:

\begin{align*} {\bf N}_{max} = \left(2^{2^{\bf E} - 1} - 1\right)2^{\bf M} + 2^{2^{\bf E} - 1}\left(2^{\bf M} - 1\right) = 2^{2^{\bf E} + {\bf M}} - \left(2^{2^{\bf E} - 1} + 2^{\bf M}\right) \end{align*}

  • новая оценка \widehat{n}также несмещённая: {\sf E}\widehat{n}(C_n) = n;

Доказательство

Аналогично доказательству утверждения для обычных счётчиков Морриса посчитаем условное матожидание {\sf E}(C_n | C_{n - 1} = y). Причём сделаем это отдельно для y \equiv -1 \pmod{2^{\bf M}}(вероятность обновления изменится в случае успеха) и y \not\equiv -1 \pmod{2^{\bf M}}.

\begin{align*} y \not\equiv -1 \pmod{2^{\bf M}} &\implies {\rm e}(y + 1) = {\rm e}(y), \quad {\rm m}(y + 1) = {\rm m}(y) + 1 \\ &\implies \widehat{n}(y + 1) = \widehat{n}(y) + 2^{{\rm e}(y)} \\ y \equiv -1 \pmod{2^{\bf M}} & \implies {\rm e}(y + 1) = {\rm e}(y) + 1,\\ &\phantom{\implies} \phantom{Z} {\rm m}(y) = 2^{\bf M} - 1, \quad {\rm m}(y + 1) = 0 \implies \\ \widehat{n}(y + 1) = \widehat{n}(y) &- 2^{{\rm e}(y)}\left(2^{\bf M} - 1\right) + 2^{{\rm e}(y) + {\bf M}} = \widehat{n}(y) + 2^{{\rm e}(y)} \end{align*}

В обоих случаях

\begin{align*} {\sf E}(2^{C_n} | C_{n-1} = y) &= \widehat{n}(y)\left(1 - 2^{-{\rm e}(y)}\right) + \left(\widehat{n}(y) + 2^{{\rm e}(y)}\right)2^{-{\rm e}(y)} = \widehat{n}(y) + 1. \end{align*}

  • коэффициент вариации (и относительная ошибка) становятся ещё меньше! Мы не знаем его точное значение, но имеется такая оценка (сравните её с аналогичной для классического счётчика Морриса):

\begin{align*} {\sf CV}\widehat{n}(C_n) \le 2^{-\frac{{\bf M} + 1}{2}}. \end{align*}
Рис. 3: Чтение и обновление счётчика Морриса с ненулевой мантиссой
Рис. 3: Чтение и обновление счётчика Морриса с ненулевой мантиссой

Алгоритмы взвешенных обновлений и распада тоже немного изменятся.

Аналогично подходу, описанному в разделе 4, чтобы эффективно выполнить взвешенное обновление, нужно понять, через сколько попыток обновления вероятность изменится. При отсутствии мантиссы вероятность меняется после каждого успешного обновления, теперь же после каждых 2^{\bf M}. А значит нам нужно распределение количества испытаний Бернулли (искомое число событий), среди которых ровно 2^{\bf M}успешных. Такое распределение называется отрицательным биномиальным.

Замечание. Существует несколько определений отрицательного биномиального распределения. Будем придерживаться написанного в русскоязычной википедии, где сказано, что это распределение задаёт не общее число событий, а число неудач. Тогда чтобы получить число событий, нужно к случайной величине добавить количество успехов:

\begin{align*} n \sim \underbrace{ NegativeBinomial\left(2^{-{\rm e}(C)}, 2^{\bf M} - {\rm m}(C)\right)}_{\textit{неудач}} + \underbrace{\left(2^{\bf M} - {\rm m}(C)\right)}_{\textit{успехов}}. \end{align*}

Чтобы не генерировать отрицательное биномиальное распределение, можно загрубить алгоритм, всегда выбирая среднее этого распределения:

Чтобы выполнить распад, будем вычитать 1из экспоненциальной части (иначе говоря, 2^{\bf M}из значения счётчика). Тогда

\begin{align*} \widehat{n}(C - 2^{\bf M}) = (2^{{\rm e}(C) - 1} - 1)2^{\bf M} + 2^{{\rm e}(C) - 1}{\rm m}(C) = 1/2\widehat{n}(C) - 2^{{\bf M} - 1}. \end{align*}

Заметим, что при {\bf M} > 0(а именно этот случай изучается в этом разделе) 2^{{\bf M} - 1} \in \mathbb{N}. Поэтому исправить оценку можно, вероятностно увеличив счётчик на 2^{{\bf M} - 1}:

7 Заключение

Счётчики Морриса — это очень круто! Пользуйтесь!

Последний раздел не содержит полезных на практике результатов, но...

8 Обобщённые вероятностные счётчики

В общем виде правило обновления счётчика определяется функцией вероятности F : C \mapsto [0, 1]:

\begin{equation*} C_{n+1} = \left\{\begin{array}{ll} C_n + 1 & \textit{с вероятностью $F(C_n)$} \\ C_n & \textit{с вероятностью $1 - F(C_n)$.} \end{array}\right. \end{equation*}

В случае счётчиков Морриса F(C_n) = 2^{-C_n}. При изучении вероятностных счётчиков мы попробовали взять линейную функцию вероятности:

F(C_n) = 1 - \frac{C_n}{C_{max}},

гдеC_{max}— некоторая константа, максимальное значение счётчика. Это привело к некоторым интересным результатам, которые будут кратко изложены в этом разделе.

Прежде чем представить эти результаты, напомним о двух математических сущностях. Полный однородный симметрический многочлен степени nот mпеременных x_1, \dots, x_m— это сумма всех возможных одночленов степени nот этих переменных с коэффициентами 1:

\begin{align*} \mathcal{H}_n(x_1, \dots x_m) = \sum_{\begin{array}{cc} & 0 \le i_j \le n \\ & i_1 + \dots + i_m = n \end{array}} x_1^{i_1} \cdots x_m^{i_m}. \end{align*}

Другая конструкция, которая нам понадобится, — число Стирлинга второго рода. Один из способов определить это число — комбинаторный: число Стирлинга второго рода \genfrac\{\}{0pt}{}{n}{m}— количество разбиений n-элементного множества на mнепустых подмножеств. Числа Стирлинга связаны с полными симметрическим многочленами:

\begin{align*} \genfrac\{\}{0pt}{}{n+m}{m} = \mathcal{H}_m(1, 2, \dots, m). \end{align*}

С помощью \mathcal{H}можно записать в общем виде вероятность того, что после nпопыток обновления значение счётчика равно m:

\begin{align*} {\sf P}(C_n = m) = \left[\prod_{k=0}^{m-1} F(k) \right] \mathcal{H}_{n-m}(1-F(1), \dots 1-F(m)). \end{align*}

Эту формулу легко доказать по индукции, но также она несложно следует из простых комбинаторных рассуждений: фактически в ней записано, что для того, чтобы получить значение m, нужны mуспешных обновлений: с 0до 1, с 1до 2и т.д., — за это отвечает множитель \prod_{k=0}^{m-1} F(k), и n - mнеудачных, которые разбиваются на mгрупп: i_1неудачных обновлений с 1до 2, i_2с 2до 3и т.д., что выражено \mathcal{H}_{n-m}.

Наконец, при использовании линейной функции вероятности F(C) = 1 - \frac{C}{C_{max}}вероятность принимает вид

\begin{equation*} {\sf P}(C_n = m) = \genfrac\{\}{0pt}{}{n}{m} \frac{C_{max}!}{(C_{max} - m)!C_{max}^n}. \end{equation*}

Это и есть анонсированный выше интересный результат. Мы заметили число Стирлинга в значении вероятности достаточно случайно и до сих пор не знаем, можно ли обосновать его присутствие комбинаторынми рассуждениями (опираясь на его комбинаторное определение). Другой вопрос — можно ли красиво записать аналогичную вероятность для счётчиков Морриса.

Математическое ожидание и дисперсия C_n(доказательства опускаем, но их несложно получить, используя формулу для {\sf P}и свойства чисел Стирлинга):

\begin{align*} {\sf E}C_n &= C_{max}\left(1 - \left(1 - \frac{1}{C_{max}}\right)^n\right) \\ {\sf D}C_n &= C_{max}^2\left(\frac{1}{C_{max}}\left(1 - \frac{1}{C_{max}}\right)^n + \left(1 - \frac{1}{C_{max}}\right)\left(1 - \frac{2}{C_{max}}\right)^n - \left(1 - \frac{1}{C_{max}}\right)^{2n}\right). \end{align*}

Оценить число событий можно по методу моментов:

\begin{equation*} \widehat{n}_{MM} := \frac{\ln \left(1 - \frac{C_n}{C_{max}}\right)}{\ln \left(1 - \frac{1}{C_{max}}\right)} \end{equation*}

или аналогично счётчикам Морриса, учитывая, что 1 + 1/2 + \dots + 1/n \sim \ln n:

\begin{equation*} \widehat{n} := C_{max}\ln \left(\frac{1}{1 - \frac{C_n}{C_{max}}}\right). \end{equation*}

Список литературы

[1] Morris, R.Counting large numbers of events in small registersCommunications of the ACM, 1978 21(10), 840-842.

[2] http://gregorygundersen.com/blog/2019/11/11/morris-algorithm/ ? хороший обзор счётчиков Морриса на английском языке

[3] https://habr.com/ru/company/qrator/blog/334354/ ? наша статья про EMA-счётчики

[4] https://habr.com/ru/post/208268/ ? сторонний материал про счётчики Морриса