
Введение
Представьте, что вы смотрите фильм с проектора. Если через луч проектора проходит человек, он создаёт тень, закрывая часть света. Зрители видят, что часть света от проектора закрывается, и понимают, что закрывает его какой-то человек (обычно это их раздражает). Зрители в данном случае повторяют действия телескопа «Кеплер», который обнаруживает вращающиеся вокруг звёзд планеты (экзопланеты), выявляя мельчайшие изменения в количестве света, поступающего от звезды, если планета проходит перед звездой. Такое явление называется транзитом. На основе данных о транзитных свойствах объектов при помощи машинного обучения возможно прогнозировать расположение экзопланет, в том числе похожих на Землю. К старту курса о машинном и глубоком обучении делимся немного реорганизованным переводом статьи о том, как тип модели ML может повлиять на качество прогнозирования. В конце статьи вы найдёте ссылку на репозиторий проекта с блокнотами Jupyter.
Всех нас интересует, есть ли жизнь во Вселенной. Проект «Кеплер» — важный шаг в поисках ответа на этот вопрос. Запуск телескопа «Кеплер» состоялся в 2009 году с целью обнаружения экзопланет, некоторые из которых могут находиться в так называемых «обитаемых зонах», где температура схожа с земной и, следовательно, может существовать вода в жидком виде и, возможно, жизнь.
Телескоп «Кеплер» движется по гелиоцентрической орбите, то есть вращается не вокруг Земли, а вокруг Солнца. В отличие от большинства других астрономических телескопов телескоп «Кеплер» в течение вот уже многих лет направлен на один участок неба и имеет широкий угол обзора — примерно 10х10°. Это примерно соответствует площади ночного неба, закрываемого человеческой ладонью на расстоянии вытянутой руки. В этой области находятся приблизительно 6,5 млн. звёзд, из которых примерно от 1 до 10 %, по всей видимости, имеют планеты, вращающиеся в плоскости, в которой их может обнаружить телескоп. За девять лет работы телескоп «Кеплер» обнаружил более 2600 планет за пределами Солнечной системы.
Что можно определить по освещённости?
Изменение уровня освещённости звезды, о котором говорилось выше, можно нанести на график, где будет отражён регулярный провал, соответствующий транзитной планете. Такой график называется фотоэлектрической кривой блеска, по нему можно получить важную информацию о планете. Анализируя изменение кривой блеска за длительный период, можно измерить продолжительность времени между транзитами и, соответственно, определить орбитальный период этой планеты, то есть время одного оборота планеты вокруг звезды. Также можно измерить глубину транзита, то есть показатель, отражающий степень «приглушения» планетой света звезды. По глубине транзита можно оценить размеры планеты: чем больше глубина транзита, тем крупнее планета, так как более крупный объект блокирует большее количество света. По кривой также можно судить о длительности транзита, то есть о времени, требуемом планете для осуществления транзита, о чём свидетельствует длительность провала в кривой блеска. Так можно получить информацию о расстоянии от планеты до звезды. При большем расстоянии планете потребуется больше времени для вращения по орбите вокруг звезды, а значит, длительность транзита также будет больше.
Какой набор данных использовался
Набор данных, используемый нами для этого проекта, очень сложен и характеризуется более чем 30 параметрами, но для понимания сути здесь мы перечислим только пять самых важных компонентов этого набора:
Идентификатор каждого объекта: выступает в качестве индекса набора данных.
Метка koi_pdisposition: содержит информацию о том, является ли данный кандидат экзопланетой или другим объектом.
Подмножество признаков: описывает транзитные свойства объекта (такие, как орбитальный период, расстояние от планеты до звезды и пр.).
Подмножество признаков: описывает событие транзитного пересечения (Transit Crossing Event, TCE) объекта (например, глубину транзита, количество планет в системе и т. д.).
Подмножество признаков: описывает параметры звезды (температуру поверхности, радиус, массу, возраст и пр.).
Ниже показана зависимость подмножества признаков от метки. Выбранные признаки были определены как наиболее важные с помощью метода анализа важности признаков, описанного в следующем разделе.
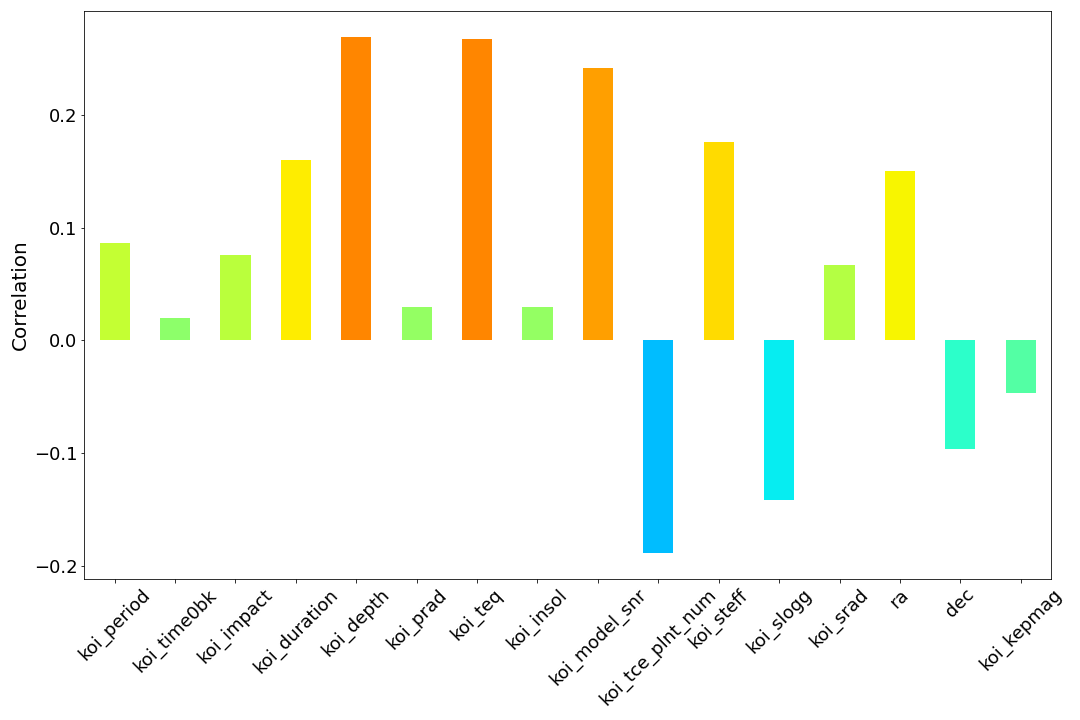
Дерево решений и важность признаков
Для фильтрации более 50 столбцов данных в наборе данных мы использовали атрибут Feature Importance (важность признака) классификатора Random Forest (Случайный лес). Случайный лес состоит из n деревьев решений, каждое из которых имеет собственные узлы и ветви. Для каждого отдельного дерева и каждой отдельной переменной рассчитывается значение "инородности", представляющее собой вероятность того, что при случайной выборке данный конкретный признак будет вычислен правильно. Важность признака рассчитывается как среднее таких значений инородности по всем деревьям, при этом наиболее важными считаются самые низкие значения инородности.

Полученные вначале наибольшие важности были довольно высокими, но это могло объясняться тем, что в признаках могла отсутствовать информация о метке классификатора, поэтому мы решили их исключить и рассчитать важность других признаков. Первоначальные расчёты показывали, что наибольшую важность имеет переменная koi_score — по сути, это вероятность того, что объект-кандидат является экзопланетой. Переменные flag и error относились, скорее, к собственному прогнозу телескопа «Кеплер», но ничего не говорили о фактических характеристиках планеты.
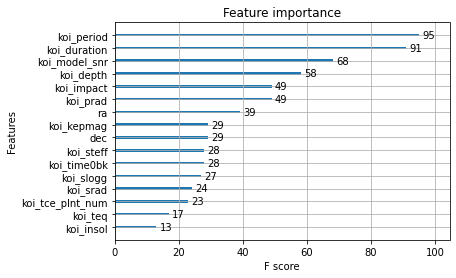
Исключив эти переменные, мы взяли за основу перечисленные выше признаки, которые затем использовали для создания собственных моделей классификации.
KNN
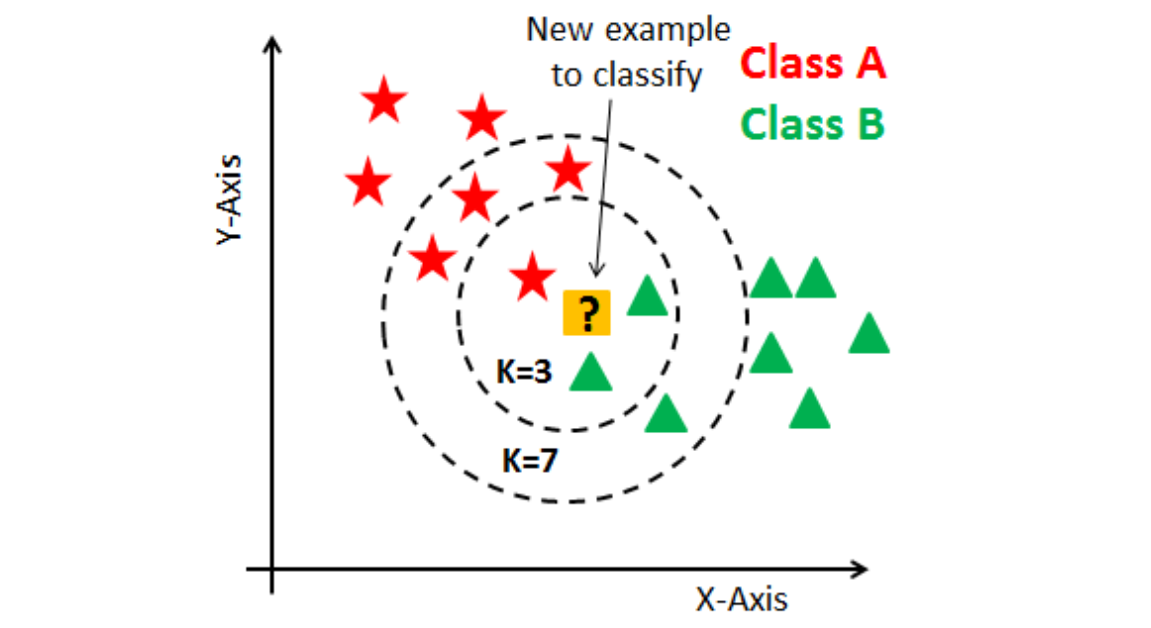
Алгоритм классификации k-ближайших соседей (K Nearest Neighbors, KNN) представляет собой модель, классифицирующую точки данных на основе меток k ближайших соседей для некоторого целого положительного числа k. Алгоритм обычно выполняется в три этапа:
Рассчитываются расстояния между точкой данных, которую необходимо классифицировать, и другими точками данных.
Находятся k ближайших соседей, исходя из того, какие точки данных находятся ближе всего к точке данных, которую необходимо классифицировать.
Посредством анализа частот других меток в k ближайших соседях определяется метка точки данных, которую необходимо классифицировать.
Мы хотим понять, являются ли интересующие нас объекты интереса миссии «Кеплер» либо кандидатами в экзопланеты, либо ложноположительными объектами. Несмотря на то что KNN считается довольно простой моделью классификации, она всё же способна выдавать очень приличные результаты. Используя наши данные, мы протестировали модель KNN при различных значениях k от 1 до 20 и выяснили, что максимальная точность на тестовых данных получается при k = 13 — 0,9289.
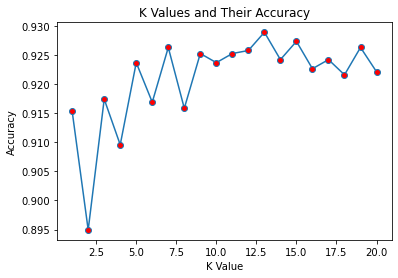
Это довольно высокая точность: с помощью алгоритма KNN можно правильно классифицировать ложноположительные объекты и выявлять кандидатов почти в 93 % случаев.

Более развёрнуто иллюстрирует результаты модели KNN матрица путаницы. Из неё следует, что алгоритм KNN даёт низкие коэффициенты обнаружения ложноположительных и ложноотрицательных объектов.
Эффективность модели KNN была нами проверена также с помощью метода k-кратной перекрёстной проверки [также метод называют k-блочной кросс-валидацией]. Этот метод перемешивает данные случайным образом и разбивает их на k групп. Для оценки эффективности модели в качестве тестовой выборки используется каждая группа, а все остальные группы используются в качестве тренировочной выборки. На каждой итерации измеряется и фиксируется точность модели. Процесс завершается, когда в качестве тестовой выборки хотя бы один раз были использованы все k групп.
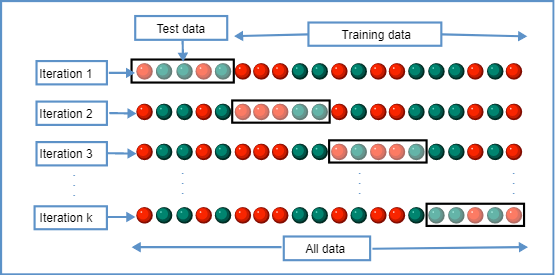
Метод k-кратной перекрёстной проверки используется для получения более точной оценки эффективности модели. При применении модели KNN мы получили точность 0,9231 после проведения k-проходной перекрёстной проверки при k = 5. В целом модель KNN показала очень высокую эффективность.
Наивный классификатор Байеса
В модели наивного байесовского классификатора (Naive Bayes) применяется теорема Байеса, позволяющая вычислять апостериорную вероятность на основе атрибутов данных. Апостериорная вероятность, обозначаемая P(c|x), представляет собой вероятность принадлежности элемента к классу с учётом его атрибутов.
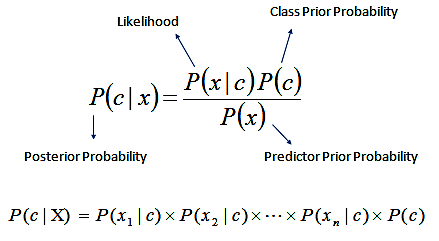
В приведённой выше формуле Байеса c означает класс, а x — атрибуты. P(c|x) — апостериорная вероятность, P(x|c) — вероятность признака с учётом класса, P(c) — вероятность класса, а P(x) — вероятность признака.
Для каждого элемента в наборе данных рассчитывается апостериорная вероятность для каждого класса, и результатом прогнозирования становится класс с наибольшей апостериорной вероятностью. Результат применения набора данных к модели наивного классификатора Байеса приведён ниже в матрице путаницы.
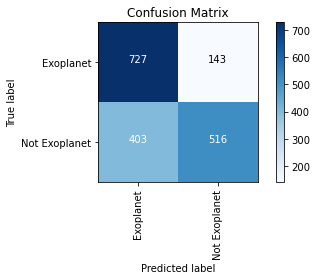
Общая точность этой модели составила 70,7 %, что является самым низким показателем среди четырёх моделей (XgBoost, KNN, Naive Bayes, SVM). Матрица неточностей показывает, что модель обнаруживает больше ложноположительных, чем ложноотрицательных, объектов, другими словами, было больше случаев, когда модель принимала объект за экзопланету, в то время как этот объект экзопланетой не являлся.
Метод опорных векторов
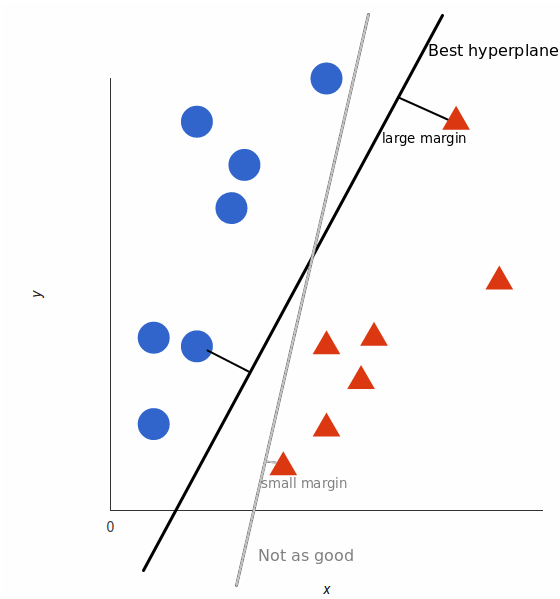
SVM расшифровывается как «метод опорных векторов» (support vector machine). Этот метод работает посредством итерационной подгонки гиперплоскости с целью разделения классов в наборе данных. Рассмотрим двухмерный пример. Различные классификации представлены различными фигурами, а границей принятия решения в данном случае является линия (в более высоких размерностях она называется гиперплоскостью). Измеряются расстояния между гиперплоскостью и ближайшими соседями из каждого класса (называемыми опорными векторами); для обеспечения большего запаса берётся максимальное расстояние.
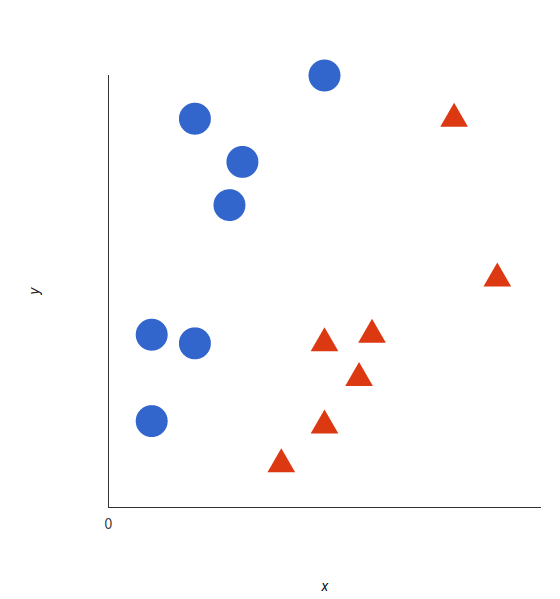
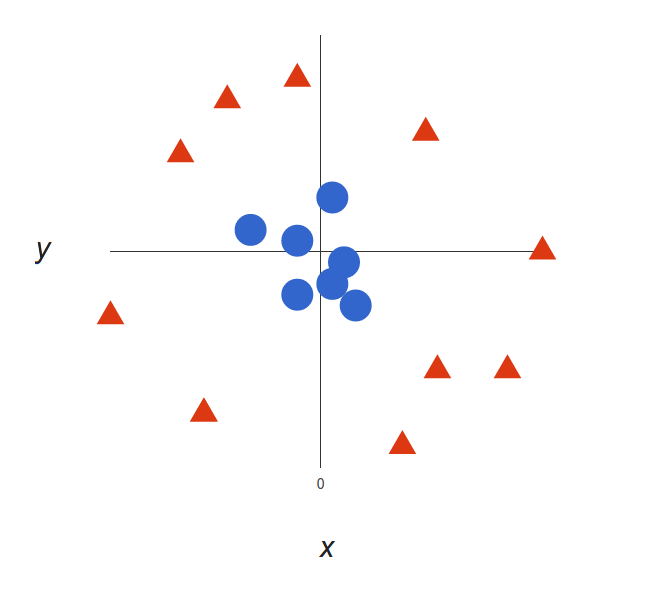
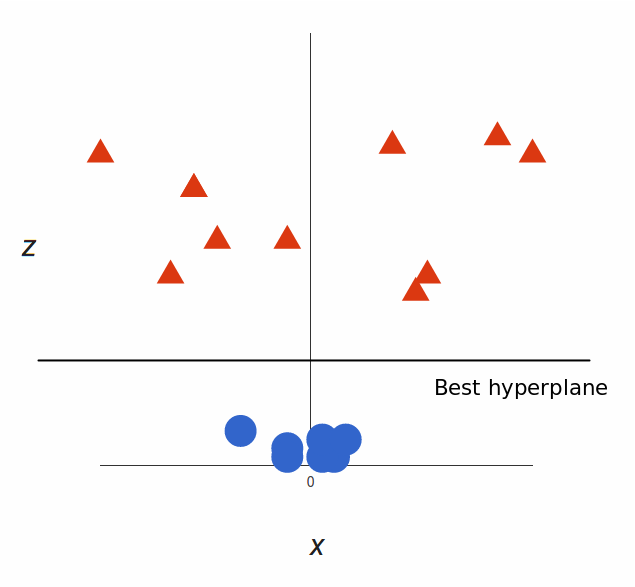
Метод также может применяться к данным, менее очевидно поддающимся разделению, например представленным ниже. Другой метод, называемый «ядра» (kernels), создаёт новую размерность как функцию существующих параметров (плоскость z). В более высокой размерности полученные данные уже легче поддаются разделению, для чего используется описанный выше метод.
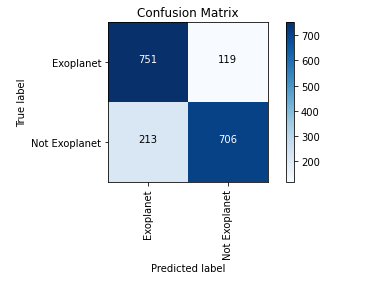
Применение модели SVM для классификации кандидатов в экзопланеты дало точность около 81,4 %. Ниже показана матрица неточностей, иллюстрирующая классификации, полученные в результате работы модели на тестовых данных.
Заключение
Анализируя данные с помощью простых статистических методов, мы смогли получить более чёткую картину важности признаков, используя алгоритм машинного обучения «случайный лес». Благодаря проведённому анализу мы смогли распознать признаки, «сливающие» данные о метке в классификатор и, по сути, содержащие ложную информацию, которую нельзя было включать в модели. После того как были выбраны наиболее важные признаки, не «сливающие» данные о метке в классификатор, мы загрузили их в ряд моделей машинного обучения и сравнили их эффективность.
Наиболее эффективной оказалась модель KNN (k ближайших соседей) — она показала точность около 92 % при использовании 13 соседей. Надёжность и стабильно высокая эффективность этой модели также была подтверждена 5-кратной перекрёстной проверкой. Второе по эффективности место заняла модель SVM (модель метода опорных векторов), её точность составила 81 %. Этот тип модели лучше всего работает с данными, относящимися к линейно-разделимому классу. Но модель KNN благодаря своей гибкости показала лучшие результаты. Ещё одна модель — наивный байесовский классификатор — проявила себя хуже всех, её точность составила около 71 %. Такая низкая эффективность, по всей видимости, объясняется тем, что базовое предположение о независимости признаков в этом наборе данных далеко от действительности.
Репозиторий проекта с блокнотами Jupyter вы найдёте по этой ссылке. В целом наша работа показала, что при использовании одного и того же набора данных эффективность машинного обучения может сильно варьироваться в зависимости от типа выбранной модели. Этот вывод подтверждает важность понимания данных и применения правильных моделей. Небольшое исследование может значительно повысить эффективность прогнозов (до 20 %) при решении таких задач бинарной классификации, как идентификация экзопланет с помощью телескопа «Кеплер».
Если вам, как и авторам статьи, интересно экспериментировать с моделями ML или вы уже многое понимаете и хотите выйти на новый уровень знаний в области машинного и глубокого обучения, то вы можете присмотреться к программе курса «Machine Learning и Deep Learning», где студенты работают с ИИ не только в практической плоскости, но также изучают всю теорию, необходимую, чтобы начать карьеру в сфере искусственного интеллекта.

Узнайте, как прокачаться и в других специальностях или освоить их с нуля:
Другие профессии и курсы
ПРОФЕССИИ
КУРСЫ

