Давайте разберемся на примере. Скажем, я хочу спрогнозировать зарплату специалиста по данным на основе количества лет опыта. Итак, моя целевая переменная (Y) — это зарплата, а независимая переменная (X) — опыт. У меня есть случайные данные по X и Y, и мы будем использовать линейную регрессию для прогнозирования заработной платы. Давайте использовать pandas и scikit-learn для загрузки данных и создания линейной модели.

import pandas as pd
from sklearn.linear_model import LinearRegression
sal_data={"Exp":[2,2.2, 2.8, 4, 7, 8, 11, 12, 21, 25], 
"Salary": [7, 8, 11, 15, 22, 29, 37 ,45.7, 49, 52]}
#Load data into a pandas Dataframe
df=pd.DataFrame(sal_data)
df.head(3)

from bokeh.plotting import figure, show, output_file
p=figure(title="Actual vs Predicted Salary", width=450, height=300)
p.title.align = 'center'
p.circle(df.Exp, df.Salary)
p.line(df.Exp, df.Salary, legend_label='Actual Salary', line_width=3, line_alpha=0.4)
p.circle(df.Exp, yp, color="red")
p.line(df.Exp,yp, color="red",legend_label='Predicted Salary', line_width=3, line_alpha=0.4)
p.xaxis.axis_label = 'Experience'
p.yaxis.axis_label = 'Salary'
show(p)

Из приведенного выше графика мы видим, что существует разрыв между прогнозируемыми и фактическими точками данных. Получается, что линейная функция не может достаточно хорошо описать наши данные. Исходя из жизненного опыта, мы так же можем предположить, что увеличение зарплаты сотрудника происходит не линейно, а в зависимости от опыта работы: чем больше опыт – тем больше повышение!

Статистически разрыв / разница между графиками называется остатками и обычно является ошибкой в RMSE и MAE.

Среднеквадратичная ошибка (RMSE) и средняя абсолютная ошибка (MAE) — это метрики, используемые для оценки работы модели регрессии. Эти показатели говорят нам, насколько точны наши прогнозы и какова величина отклонения от фактических значений.

Технически, RMSE — это корень среднего квадрата ошибок, а MAE — это среднее абсолютное значение ошибок. Здесь ошибки — это различия между предсказанными значениями (значениями, предсказанными нашей регрессионной моделью) и фактическими значениями переменной. По своей сути разница лишь в том, что RMSE из-за квадрата в формуле будет сильнее наказывать нас за ошибку, т.е. будет увеличивать вес / значение самой ошибки. Метрики рассчитываются следующим образом:

Yi – настоящее значение

Yp – предсказанное значение

n – кол-во наблюдений

Scikit-learn предоставляет библиотеку показателей для расчета этих значений. Однако мы будем вычислять RMSE и MAE, используя приведенные выше математические выражения. Оба метода дадут одинаковый результат.

import numpy as np
print(f'Residuals: {y-yp}')
np.sqrt(np.mean(np.square(y-yp)))  #RMSE
np.mean(abs(y-yp))  #MAE
#RMSE/MAE computation using sklearn library
from sklearn.metrics import mean_squared_error, mean_absolute_errornp.sqrt(mean_squared_error(y, yp))
mean_absolute_error(y, yp)

6.48
5.68

Давайте попробуем составить полиномиальное преобразование (X) и совершить предсказание с той же моделью, чтобы посмотреть, уменьшатся ли наши ошибки. Для этого используем Scikit-learn PolynomialFeatures

from sklearn.preprocessing import PolynomialFeatures
pf=PolynomialFeatures()     
#Linear Equation of degree 2
X_poly=pf.fit_transform(X) 
lm.fit(X_poly, y)
yp=lm.predict(X_poly)

То же действие можно сделать вручную и для любой степени полинома:

def generate_degrees(source_data: list, degree: int):
       return np.array([source_data**n for n in range(1, degree + 1)]).T

Вычисляем метрики:

#RMSE and MAE
np.sqrt(np.mean(np.square(y-yp)))
np.mean(abs(y-yp))

2.3974
1.6386

На этот раз они намного ниже. Давайте построим графики y и yp (как мы делали раньше), чтобы проверить совпадение:

Разрыв между двумя строками уменьшился, а метрики качества модели стали лучше!

Давайте разберем подобную задачу не на искусственных, а на реальных данных. Посмотрим на уже предобработанные данные по входам в систему онлайн трейдинга.

В переменной y_train хранится количество людей, зашедших во время x_train. Вполне обычная задача, решаемая линейной регрессией:

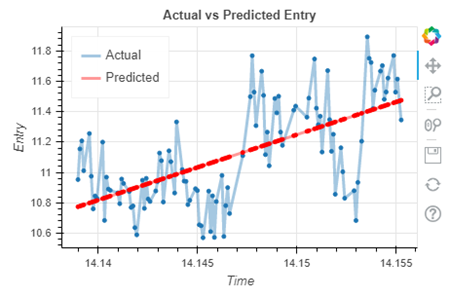
Модель отработала с ошибками MAE и RMSE в 0.602 и 0.616 соответственно. Такое высокое число ошибок связанно с тем, что данные имеют сильный разброс относительно линии регрессии. Однако, мы можем предположить, что для такого примера так же недостаточно лишь функции линейной регрессии. Давайте проверим эту гипотезу и попробуем применить полиномиальную регрессию и посмотреть метрики качества модели для полинома 2 степени:

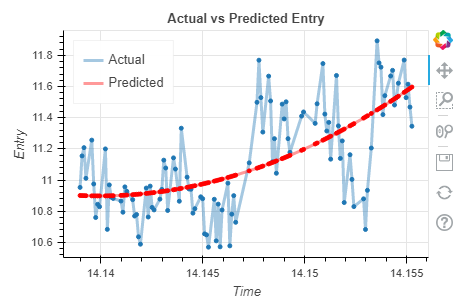
Данная же модель отработала с ошибками MAE и RMSE в 0.498 и 0.543 соответственно, и визуально мы можем интерпретировать, что наша модель лучше стала описывать данные.

Почему же не использовать функцию большего количества степеней, 3, 15, 100? Ведь тогда метрики качества модели будут лишь улучшаться! Но не все так просто. Конечно, модель лучше станет описывать наши данные, а при совсем большом количестве степеней график станет аналогичен изначальному графику, но обобщающая способность модели сильно снизится, и она будет работать хорошо только лишь в данном наборе данных и не сможет должным образом сделать predict новых значений.

Таким образом мы разобрались в основных метриках качества работы модели и на их примере показали, что использование полиномиальной регрессии зачастую дает лучшие результаты, чем линейная. Однако всегда нужно отталкиваться от поставленной задачи.

Хочу отметить, что повысить метрики качества модели MAE и RMSE можно и другими способами. Некоторые из методов, которые мы можем использовать, включают в себя:

• Функции преобразования / масштабирования

• Обработка выбросов (если их много)

• Добавление новых фичей

• Использование разных алгоритмов

• Настройка гиперпараметров модели