1 / 0

При освоении программирования встречается один смешной спор, начинать адресацию элементов в массиве с единицы или с нуля. С одной стороны, если у тебя один элемент в массиве, то и номер у него должен быть равен единице. С другой стороны, когда выбираешь куда поместить первый элемент, то надо подыскать место, равное количеству элементов до помещения — нулевое. То есть, чему равен адрес последнего элемента — количеству элементов до помещения или после? — Вот в чём здесь вопрос.

Но, как бы то ни было, для себя я просто разделили на два понятия: индекс и номер. Индекс относится уже не к элементу, а к его месту, к величине отступа, которая для элемента номер один равна нулю. Элемент с индексом ноль — первый. Всё просто.

Соревнование между нулём и единицей может быть описано более детально.


Исторически счёт принято начинать с единицы, и это оправдано, так как отводит нулю его место — то что было в самом начале, до начала счёта. И этим указывает, что такое сам счёт. Это нахождение элемента между предыдущим и предстоящим. «Предыдущий» в начале счёта ноль, «предстоящий» элемент тоже вполне определён. Основное действие — то что понимается под «предыдущим» меняется на то что получено, и счёт можно продолжать.
Предстоящий элемент в такой схеме счёта недостижим, и пессимистично называется «бесконечность».

После того как у нас получено два элемента можно решиться на нетрадиционное действие — оба полученных элемента применить как предыдущий и предстоящий. И таким образом пойти не вперёд, но и не назад, а «вглубь». Более того, даже с самого начала первый элемент можно использовать не как «предыдущий», а как «предстоящий», с повторным использованием в качестве «предыдущего» элемента ноля. И тогда элемент, полученный после единицы, будет не двойкой, а двойкой «обращённой».

Общий порядок, в котором из двух элементов один всегда больше другого, сохранится, но порядок счёта уже не всегда идёт в направлении возрастания. В целом, схема счёта сильно изменится, добавится выбор: полученный элемент ставить на место меньшего в следующем поиске, или на место большего. Схема счёта превратится в бинарное дерево — каждый элемент в нём содержит две возможности для движения дальше.

Каждая ветка такого счёта представляет собой аналог всего дерева — это самый древний и самый простой фрактал.

Самое интересное, что такой фрактал очень хорошо кодируется, каждый элемент обозначается двумя кодами, взятыми из прямого счёта. Для того чтобы закодировать текущее число, нужно сложить коды границ — для первого кода сложить первые, для второго сложить вторые. А коды для первоначальных границ это и .

На первом шаге получается . А после этого есть выбор: пойти либо в большую сторону, либо в меньшую, и для каждого следующего шага придётся выбирать. Можно было бы сказать, что эти два числа составляют дробь, но существует явное отличие: среди таких чисел никогда не встретится дробь, которую можно сократить. Просто потому, что первой при таком спуске встречается сокращённая дробь, а все последующие числа будут либо больше, либо меньше.

Кроме сокращения ничего не мешает дроби быть на этом дереве, и они там присутствуют все без исключения. Так что, любые два натуральных числа можно объединить в пару, от которой отделить общий множитель, и останется рациональное число, представляющее собой не просто пару чисел, а натуральное количество шагов, для каждого из которых сделан бинарный выбор. Либо просто единица, если без шагов.


Количество шагов без изменения направления напрямую отражается в элементах цепной дроби:

— Означает, для достижения этой дроби от единицы нужно пройти в большую сторону 3 раза, затем в меньшую сторону 7 раз, затем в большую сторону 15 раз.

Можно предположить, что при шаге от нуля тоже существовал выбор — идти в большую или меньшую сторону, этот выбор соответствует знаку числа. Две ветки могут образовывать одну такую линию, которая включает в себя ноль, а на всех остальных шагах выбирается максимальное отличие. Так и находятся все целые числа, .

При визуальном анализе, если расставить на плоскости элементы дерева по координатам, соответствующим кодам, то каждая точка будет иметь одну проекцию из точки ноль-ноль на линию, в которой числитель единица. Каждая проекция на этой линии всегда будет находиться строго между проекциями от границ своего выбора. И наоборот, каждой точке проекции будет соответствовать число.

А теперь можно сыграть в игру. Ведущий загадывает число, а игрок отгадывает. Представь, что ты игрок. Ведущий будет отвечать только «угадал» или «больше/меньше» — про отношение загаданного числа к твоему.


После множества последовательных «больше» и «меньше» у тебя может возникнуть ощущение, что ведущий не загадал никакого числа, что ты спускаешься по бинарному дереву, а он просто наугад говорит «больше» или «меньше». И ты прав, есть такой вариант. Но между собой варианты — загадал он или нет — ты не отличишь.

Даже при нескончаемых вопросах можно считать, что существуют иррациональные числа, которые содержат неограниченное число бинарных выборов, а ведущий просто загадал одно из них.

Что будет, если первым числом спросить о единице, а ведущий после этого в принципе не перестанет отвечать «меньше»? Окажется, что он загадал ноль. Но ты начал с единицы, и попался.

А если это будет настоящая угадайка, то узнать, угадал ты или нет, не получится, тоже надо будет угадывать. В такой игре достаточно обойти число, ведущему в момент угадывания рандомно сказать «больше/меньше», а затем всегда повторять противоположное. И в конце мы приблизимся к тому же результату. После этого никаких сомнений, что — это лишь мутный вариант единицы.

Конечно, это странная игра — в которой надо угадать, выиграл ты или нет. Но «угадай-ка» — она такая, кто начал играть, тот доверился ведущему.

Зря-зря

Если для иллюстрации шаги в большую сторону изображать линиями по одной диагонали, а шаги в меньшую сторону вдоль другой диагонали, начать с точки, обозначающей ноль (или единицу), и каждый раз уменьшая длину линии в два раза — мы получим вполне компактный рисунок в виде треугольника. В нём обозначенные числа чётко поделятся на лежащие на нижней линии и на расположенные выше.

То есть, числа чётко делятся на два вида, рациональные и иррациональные. Но в процессе игры всегда есть текущий шаг, и числа делятся на три вида, «уже угаданные на данном шаге», «пока что не угаданные» и «числа, которые не зная, не угадаешь».

Можно разделить на три вида совсем по-другому. На «угадываемые», «не угадываемые, но загаданные» и «вообще не загаданные». Ведь причина невозможности угадать может быть не только в бесконечной цепочке необходимых вопросов. Что если другой причины каждого ответа ведущего, кроме желания продолжить игру, нет? Он и сам не знает числа.

Объединяя, вместо двух типов чисел нужно отметить четыре типа. Рациональные делятся на обозримое число шагов и необозримое, а иррациональные делятся на чёткие и мутные. Для рациональных деление оставляет эти числа в рамках общей группы. А для иррациональных — нет, мутные числа исключаются из чисел. Но и после этого не стоит ожидать отсутствия подвоха, так как кто угодно может загадать мутное число, пользуясь тем, что угадывающий не может это распознать в принципе. Это, так сказать, троллинг, который возможен всегда и везде — в каждой игре.

Не зря утопили Гиппаса, сделавшего открытие о такой человеческой беспомощности. Ну, или зря.

Спуск

Количество шагов для такого угадывания числа я бы назвал уровнем погружения. У каждого рационального числа есть соответствующая характеристика, выражающаяся натуральным числом. Нулевой уровень будет у нуля (или у единицы, если выбор знака не считать уровнем).

Легко ли по обозначению числа в виде дроби узнать, в большую сторону или меньшую был первый шаг после единицы? Легко — достаточно сравнить эти обозначения, и если знаменатель меньше числителя, то определённо — шаг был в большую сторону.

Легко ли по обозначению узнать, в какую сторону был совершён последний шаг? Нет, последовательность выяснения направлений шагов по обозначению проста только от первого к следующему. Узнали, что числитель больше знаменателя — выяснили первый шаг. Затем от числителя можно отнять знаменатель, и тогда для новой дроби мы как будто исключили этот шаг из последовательности. И по тому, что будет у неё больше, числитель или знаменатель, можно будет узнать про второй шаг исходной дроби. И так далее.

Когда при такой цепочке расчётов мы придём к тому, что числитель равен знаменателю, это будет значить, что цепочка закончилась. Но если они ещё будут отличаться от единицы, значит исходная дробь могла быть сокращена. Число, на которое можно дробь сократить, правильно называть наибольший общий делитель числителя и знаменателя. Если два числа перемножить и поделить на наибольший общий делитель, то получится наименьшее общее кратное. В нём все три части: собственная для первого числа, собственная для второго числа и общая часть для обоих чисел при перемножении встречаются по одному разу.

Запомнить, что из этого что, очень просто: «наибольший...» всегда меньше, чем «наименьшее...».
«Л» — Логика.

Произведение:

На этом изображении умножение представлено как сложение степеней.

Деление как разница степеней:


Дерево рациональных чисел, о котором здесь было рассказано, называется «Дерево Штерна — Броко».

Для каждого рационального числа есть парное число — в котором уровней столько же, но значения выбора направления при погружении расположены в обратном порядке. И парные числа тоже можно организовать в дерево, «Дерево Калкина — Уилфа». В таком дереве для получения числа следующего уровня нужно на выбор, либо к числителю добавить знаменатель, либо к знаменателю числитель. И хотя порядок расположения элементов в этом дереве в поперечном направлении не сохраняет последовательность возрастания, очевидно, выяснять направление погружения здесь удобнее наоборот, начиная с последнего выбора.

В порядке возрастания:

Жаль, но для иррациональных чисел пары не найти — выбор у парного числа определяется начиная с последнего уровня, а у иррациональных чисел последнего уровня нет. Просто нет.

Простые числа

Все дроби входящие в дерево не сокращаются. Если среди дробей вида ни одна дробь не сокращается, то — простое число. Это даже видно на схеме. Пока Эратосфен придумывал своё решето, стопроцентная доля несокращаемых дробей на схеме дерева наглядно оставалась у простых чисел.

Если дробь принадлежит дереву, тогда число тоже принадлежит дереву, в виде . Особенность простых чисел в том, что если простое, то не надо проверять, сократится ли оно с или нет, так как если , то точно не сократится. Таким образом, часть рациональных чисел определяется не двумя, а одним натуральным числом.

Экономия.

Для таких дробей, как и для всех, которые не сокращаются, числитель и знаменатель можно возвести в любую натуральную степень, и она не сократится. Но для этой дроби можно возвести в любую степень отдельно :

И она тоже не сократится. Малая теорема Ферма состоит в том, что при будет

И значит при

То есть, остаток деления на простое число результата возведения в варьируемую степень — периодичен, и его период на единицу меньше этого простого числа — степень совпадает с единичной, а не с нулевой степенью.

Доказательство: При простом произведение при изменении одного только никогда не дублирует тот же самый остаток — иначе разница была бы кратна . Набор вариантов остатков будет повторять натуральные числа меньше . Значит, если мы перемножим все варианты , при заданном , пробежавшись от до , результат хоть и будет кратен , по остатку будет аналогичен произведению всех чисел меньше . Если мы остаток поделим на сам остаток, получится один, но это деление можно воспроизвести установив в каждом множителе в . Тогда мы рассматривали бы только остаток , так что он единица.



Числа и дают одинаковые остатки при делении на . Из-за этого при все натуральные числа можно разделить на два класса, один из которых означает, что можно как минимум двумя способами выразить , где — из того же набора . А числа из второго класса так выразить не получится. При простом количество чисел в обоих классах одинаково. То есть, относительно простого числа все целые числа делятся не на два, а на три типа. Вторых и третьих поровну.

Золотая середина

Каждый шаг спуска по дереву рациональных чисел может быть характеризован не только как шаг в большую или меньшую сторону, шаг начиная со второго либо повторяет направление предыдущего шага, либо его меняет. Из-за этого можно организовать спуск без сохранения предыдущих границ, достаточно сохранить предыдущее число. Каждый шаг в кодах будет вычисляться либо как повторное добавление разницы с предыдущим числом, либо как прямое сложение текущего и предыдущего, при развороте оно выступает в качестве границы.

В этой схеме можно выделить пару особых чисел — которые получены постоянной сменой направления. Это такое отношение, в котором периодически то к числителю добавляется знаменатель, то к знаменателю числитель, образуя значения из последовательности фибоначчи, и соответствуя золотому сечению.

Закодированная последовательность выбора:

Порядок для таких чисел легко обратить, даже при неизвестном результате вариантов обращения всего два — в соответствии того, каким в результате будет самый первый выбор.

Предыдущее и следующее

Для числа, полученного последовательным погружением, зная предыдущее число легко восстановить последовательность выборов в обратном порядке, у одного из вариантов отклонение меньше. Но даже если предыдущее число неизвестно, о его характеристиках кое-что можно сказать.

Для соотношения дробей из натуральных чисел

И условием и следствием является

Для начальных дробей . Все последующие дроби продолжают выполнять это соотношение, и сохраняется.

Это можно представить как учёт различия отношений числителей и знаменателей

А можно представить как изменение величины дроби. Так что, для дробей и , идущих при погружении последовательно, выполняется одно из двух равенств, в зависимости от направления смещения величины, но независимо от порядка дробей в последовательности:

Для двух шагов подряд формула выглядит симметричнее:

Прежде всего потому, что второй шаг может отменить первый.

Уровни

График разграничения уровней:



Рациональные числа одного уровня — для построения которых нужно сделать одинаковое количество бинарного выбора — изображены здесь как граница области одного цвета. Дроби, которые могут быть сокращены, представлены на этом графике местами, через которые не проходит граница цветовой области.

Если соответствующие места выделить, то график будет выглядеть так:



Выделены сокращающиеся дроби.

В этом представлении простым числам больше подходит название «бешенные числа» — они соответствуют такому удалению от центра, на котором на всей линии нет ни одного места, где бы цвет не переключился.

Дроби, в которых один из элементов ноль, могут быть сокращены на оставшийся элемент. Поэтому эти точки тоже можно отметить.



У таких дробей нет своего уровня, не смотря на то, что соответствующие точки лежат на границе области.

Вот ещё пара графиков, с чуть более различимыми соседними цветами:





Если нужно, вот ссылка на хайрез.

Что было до нуля

А что если ноль — это не начало цепочки выбора?

Можно использовать определение «достижимых» чисел, что каждое число связано с тремя другими без образования циклов — и это определение предельно симметрично. Для нуля — единица и минус единица являются вариантами выбора для шага вперёд. Осталось выяснить, что за элемент является для нуля возвратным.



Для того чтобы выяснить как это кодировать можно попробовать восстановить дерево в обратную сторону, исходя из свойства золотого сечения, ведь числа Фибоначчи можно рассчитать и обратно. Тогда схема дерева будет выглядеть так:



Видно, что для части обратных чисел кодирующие дроби имеют противоположный знак одновременно и у числителя и у знаменателя. Это можно поправить.

Посмотрите на здоровое дерево рациональных чисел и на дерево курильщика:

Деревья аналогичны, но во втором удалось завернуть «возвратную» часть всех чисел на половину ветки, считавшейся от ноля «вперёд». При завороте для отрицательных чисел сдвинулись коды, к знаменателю добавлена абсолютная величина числителя. Бесконечность при этом вошла в схему без различия в знаке, так же как ноль.

Так что, даже если добавить «возвратные» числа, они все поместятся в обычных кодах. Можно изобразить это дерево так:



Числа так же располагаются по сетке:



Самоподобие позволяет анимировать это дерево:



Существует несколько моделей для интерпретации числа обратного нулю.

В симметричной схеме можно выделить две ветки, между которыми нет выбора, они просто являются предыдущими друг для друга. Тогда будет: одна ветка рациональных чисел, с листками иррациональных, и такая же ветка обращённых по порядку чисел, в том числе «количественно максимальное» число.

Проблема этой схемы только в том, что в ней нет места «среднему» числу: хотя край веки от нуля идёт к «максимальному», а край ветки от «максимального» идёт в ноль, определить, где они пересекаются нельзя без введения такой же структуры чисел, наложенной на оригинальную структуру как бы накрест. Для получения средних от средних нужно будет опять добавлять веток.

Другая модель состоит в том, что возвратным к нулю является «осевое число», а в качестве возвратных к нему определены положительная и отрицательная середины между минимальным и максимальным количественным числом.

Для отражения максимального количественного числа нужно добавить такую же структуру, с тем же осевым числом, но с промежуточным расположением веток относительно веток первой структуры.

И от этого вместе с «максимумом» сразу появятся «середина до середины».

Так делить можно и дальше, построение средней ветки аналогично нахождению промежуточного числа. При дальнейшем делении ветки множатся, повторяя в своей структуре не только свою внутреннюю часть, но и самих себя. Даже последовательность число-ветка можно продолжить и брать порядок из самих чисел. Лишь бы порядок числа не догнал его самого.

Ветки можно от середины добавлять и в сторону возрастания и в сторону убывания, приближаясь либо к количественному максимуму, либо количественному минимуму. Добавление веток в сторону убывания происходит по порядку приближения к нулю, предел приведёт к самой ветке нуля. Точно так же как нет «соседних» чисел — предел приближения ведёт к самому числу — нет и «соседних» веток. Это иллюстрация, почему счётная и несчётная бесконечности различаются принципиально — это разные стороны предела приближения к такому месту, которого нет. Просто нет.

Вообще без нуля

Рациональное число кодируется ограниченной последовательностью бинарного выбора. Но теперь выбор можно определять и в обратную сторону. И теперь из двух рациональных чисел можно составить двойное число, в котором выбор от нуля происходит как вперёд, так и назад. В точке начала отсчёта будут соединены две последовательности.

Чтобы это число было не просто парой рациональных чисел, можно добавить, что точка соединения последовательностей не важна, и бинарный выбор может свободно перетекать из одной последовательности в другую. Рациональное число и его обращение, с обратным порядком выбора — объединяются в одно число, и становятся как две крайности в вариантах перетекания.

Для многих иррациональных чисел бинарный выбор повторяется циклически, такие числа тоже можно соединить со своим обращением. Тогда из-за неважности положения точки соединения в одно двойное число будет объединено сразу несколько чисел, количество которых равно размеру цикла выбора. Из-за этого объединения количество двойных чисел может казаться меньшим, чем пар одинарных.

Числа с неограниченным и не циклическим выбором тоже можно было бы представить как двойное число, но в одном таком двойном числе будет объединено неограниченное количество одинарных чисел, так что возникнет вопрос — в случае такого иррационального расширения не сильно ли двойных чисел будет меньше, чем пар из одинарных? Впрочем, какая разница.

Сравнивать на больше/меньше двойные числа можно только приведя начальную точку выбора к нулю, так как только выбор вперёд определяет увеличение или уменьшение числа, выбор назад не может определять направление различия. Неограниченные двойные числа нельзя привести к начальной точке отсчёта, поэтому их и нельзя сравнить на больше/меньше. Ну и ладно.

В целом получилось, что число задаётся двумя точками на двойном бинарном дереве. При этом важно только различие положений. При возможности выбора на бесконечном удалении получившиеся числа будет невозможно сравнить. Даже выяснить факт равенства двух таких чисел и то задача в общем случае неразрешимая. Стоп, приехали.

Троллинг, когда две бинарные бесконечные последовательности надо сравнить, не указывая точного соответствия позиций — достаточно тонкий. И выяснение факта конечного значения для разницы позиций это очень хорошее начало для определяющего эту идентификацию сравнения всей этой бесконечности вариантов выбора.

Пожалуй, лучше вернуть ноль на место начала отсчёта.

Часть вторая

Двойные функции

Это функции от двух аргументов, но с особенностью, что функция зависит от соотношения этих чисел, а не от них самих — иначе это были бы обычные функции двух аргументов. Но и от функции одного аргумента двойные функции отличаются, так как подставлять в такую функции вторым аргументом, аналогом знаменателя, ноль вполне допустимо. Недопустимо только чтобы оба аргумента были нули.

Определим две двойных функции от натуральных чисел и .

Ещё одно уточнение на счёт двойных функций: если функция нечётная, изменение знака у первого аргумента приводит к изменению знака значения, а вот изменение знака у второго аргумента может изменить значение совсем по-другому — потому что изменение знака второго аргумента приводит ко второму, независимому от первого, значению функции. Эти функции поэтому и «двойные», что у них на одно отношение в дроби существует два значения, в зависимости от комбинации знаков. Если один аргумент ноль, различие идёт по знаку другого аргумента.

Определим третью двойную функцию

Получилось, что она имеет параметр. При и повторяет одну из предыдущих функций. А при

Результат как бы совмещает два предыдущих определения функций в одном.

Все три функции потом будем использовать как идентификаторы для точек — чтобы разным комбинациям соответствовали разные значения. Другими словами, чтобы по значению можно было определить аргументы, с точностью до общего коэффициента.

Взаимосвязь координат в обращённом виде

Показывает, что при значение будет браться из второй части двойной функции.

Из

Можно вывести оба обратных пересчёта координат:

Видно, что для пересчёта нужно не только знать, какой из четырёх переходов используется, формула может для одного перехода иметь различный вид. Представлены три варианта.

Преобразование можно повторять по нескольку раз. Если первый шаг преобразования координат будет

То второй шаг приводит к:

Если шаг сделать раз, то коэффициенты будут биномиальные, как в разложении .

Если затем каждый шаг сократить в раз, то получится:

Теперь можно приравнять к нулю.

Вот это — поворот. Достижение соответствия координат теперь наступает раньше, чем достигает единицы — при .

Переопределение функции с изменением роли параметра со сдвига на вращение даёт одно преимущество: при нескольких последовательных преобразованиях с заданными параметрами результат получается такой же, как при одном преобразовании, с параметром, равным их сумме. Обратная сторона этого преимущества в том, что зависимость результата от параметра стала периодической. То есть, допускается неограниченное количество вариантов параметра с тем же результатом.

Из связи между этими двумя типами преобразования можно вывести равенство

Для произвольного угла значение коэффициента будет

Этот коэффициент — именно то что сокращается при уравнивании аргументов двойной функции.

Чтобы выразить параметры в обратную сторону, через , сначала выразим производную.



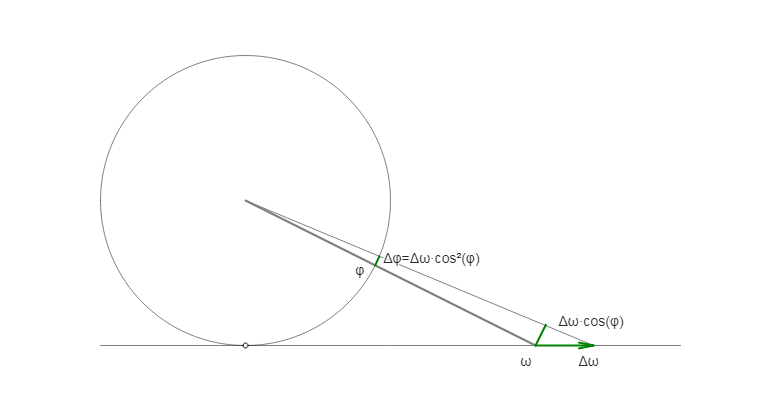
Различие направления и скорости приводит к произведению двух косинусов.

Так как , то

Прежде чем проинтегрировать эту производную, можно заметить что

Это преобразование при имеет смысл развернуть:

Мы на ограниченном участке значений обратили зависимость , которая в раскрытом виде выглядит как

Можно использовать для определения значения :

Двойные числа

Пока что была определена только взаимосвязь

Теперь можно эти функции определить.

— будет краткой записью двойной функции, когда второй аргумент единица.

Функцию можно наделить свойством нечётности.

Тогда

И ясно, что когда то . И всё это равно числу, у которого не важен знак. В общем-то, ноль сгодится.

Можно продолжить и добавить свойство функции

Тогда при :

— Немного рекуррентности. И конечно, теперь будет точно

Эти функции можно назвать характеристиками аргументов, совпадает со степенью аргумента, как одной дроби. По степени числа всегда можно определить само число. Да и у числа чаще всего можно определить степень.

Вычисляется степень как логарифм по выбранному основанию.

Теперь можно начать использовать двойные числа.

Комплексное число — это такое число, у которого степень числа характеризуется наряду с обыкновенной степенью, ещё и поворотом. А так как поворот периодичен, то поворотная часть степени позволят задавать одно число несколькими значениями степени, произвольная часть здесь обозначена . У самого числа тоже будет две части.

Составляющие называются реальной и мнимой частью. Мнимая часть может кодироваться как обычное число, степень которого изменена на повёрнутую, то есть, число будет умножено на единицу с поворотной степенью, она же половина от разворотной, четверть циклической.

Получается, функция определения степени — многозначна. Зато обратная функция, определения числа по степени, экспонента, однозначна. Точнее, если основание отрицательное, то выбрать главный результат решения нужно будет как минимум из двух вариантов, ну а если не отрицательное, тогда главный вариант, конечно, один.

Здесь выполняет соотношение и не влияет на результат.

Сравнение чисел на больше/меньше всегда говорит о действительных числах, так как направление различия комплексных чисел не ограничивается одним только знаком.

На число можно ввести условие , условие , и лучше, конечно, ему быть больше единицы. Значение можно определить исходя из желания сделать число целым.

Тогда .

Но можно сделать целым, оставив величину периода повтора у в .

Тогда нужно будет использовать в показателе константу

Поворотная степень вместо

Будет выглядеть как

Производная такой функции по убирает первое слагаемое, у других слагаемых понижает уровень — получается то же что и было, производная этой функции совпадает с ней самой.

Все эти единицы — значение производной соответствующего порядка. Любую функцию можно раскладывать на значения производных в нуле, а потом собирать обратно. Разложения двух функций, , довольно простые:

Но если из степенной функции отнять единицу, то получится ряды, которые начинаются одинаково, и продолжаются один — нулями, другой — единицами.

Их отношение имеет интересное разложение:

Вся это скачущая последовательность чисел приводит к тому, что функция с возрастанием приближается к нулю. А судя по нулям на чётных местах, функция , оказывается, чётная.



Разложение на коэффициенты сбора производных как будто показывают внутренности функций.

Обмен между аргументом и значением для функции будет натуральным логарифмом, с основанием :

Его производная

С обращением знака аргумента будет

Функция обратная к уменьшенной экспоненте раскладывается с отделением :

Вот что можно уже сейчас заметить: функция , оказывается, нечётная.



Развёртку дроби можно провести и над

Исходя из этого нечётность функции

Может быть выражена как

Получилась отличная троллинг-формула. Подтвердить её можно было бы только если реальная часть была бы и больше, и меньше нуля одновременно. Такой области значений нет. Если наоборот, и не больше и не меньше нуля, но и сам при этом не равен нулю, то последовательные суммы мнимых степеней описывают бесконечно повторяющиеся круги, сходящиеся, судя по формуле, на . Точнее, отклонения обеих частей в разные стороны от этого значения при суммировании были бы скомпенсированы. Впрочем, из-за симметрии, это действительно, плюс сокращаемая при сложении мнимая часть. Но области схождения рядов в скобках всё равно не пересекаются, формула не работает.

Если дроби не разворачивать в суммы, выражение симметрии остаётся верным

Развернуть можно только ту часть, которая сойдётся обратно. Обычно одна из частей точно сходится. Но при чисто мнимом не сходится ни одна.

Вот бы, наоборот, обе сходились. Центр любой окружности, которую образует в комплексном пространстве последовательность суммирования, лежит на линии , и условная сумма

Полностью согласуется с формулой вычисления конечной суммы, если допустить, что степень в числителе перестаёт влиять на результат.

Для того чтобы сумма сходилась её можно определить иначе, как специальная циклическая сумма.

Причём, даже если сумма является циклической и условно показывает где центр этого цикла, важно выделять из всего цикла первый шаг. Центр указывается относительно начала именно первого шага. Иначе всё циклическое приводило бы в сумме к нулю.

Если использовать развёртку

Соответствующее уравнение симметрии будет

А нарастающая сумма при не будет уходить из области , но при этом всё равно наматывает круги вокруг точки схождения.

Биномиальная свёртка

Функция по определению выполняет равенство

Если это равенство выразить через ряды производных, будет:

Добавим единицу в левый множитель правой части, изменив и левую часть.

В составе функции слагаемое порядка к заданному коэффициенту имеет множитель, все коэффициенты у экспоненты единичные, поэтому произведение может быть выражено как свёртка

Коэффициенты для отдельных степеней :

При умножении обоих сторон на справа получается биномиальный коэффициент.

Так как , то можно упростить, уменьшив диапазон.

Свёртка биномиальных коэффициентов с этими числами, называемыми числами Бернулли, даёт единицу только при .

По этому признаку и получается их вывести:



Доказать, что числа Бернулли с нечётным индексом, кроме первого, равны нулю можно так:

— Нечётная часть у функции даже в удвоенном виде не выше первой степени.

Если к аргументу добавить как множитель мнимую единицу, , реальная часть обратной функции будет просто .

У этой функции есть другой метод образования



На этой иллюстрации видно, что для того чтобы получить функцию на третьей строке можно перемножить не только те функции, которые расположены выше, но и те, которые расположены ниже, только таких будет неограниченное количество.

Для аргумента это станет

Это Формула Валлиса. Если вдруг захочется на ней применить корень, то возникнет борьба масштабов:

Здесь — обыкновенный двойной факториал. Чего только двойного не бывает.

Наверное, доказать, что раскладывается в произведение не просто. Но после этого можно обнаружить, что третье число (с индексом ) в разложении на производные, , если проследить соответствие по свёртке, получается из суммы

Что в более привычном виде выглядит как

Следующий коэффициент выражается так:

Что означает, что

Если не выбирать множители по порядку, а просуммировать все варианты, скомпенсировав повтор и различие порядка выбора, то суммирование будет

Как результат:

Расчёт разницы:

И так далее.

Происхождение чисел Бернулли

Одно из применений чисел Бернулли — суммирование степеней натуральных чисел.

Начнём с бинома Ньютона:

Можно раскрыть скобки и обозначить коэффициенты. И ещё перекинуть первое слагаемое налево.

Если зафиксировать и просуммировать такие разложения для всех , начиная с нулевого, то в результате в левой части останутся только крайние слагаемые, а в правой части вместо степеней будут суммы степеней.

Например:

Переписав с уменьшенным на единицу , и немного преобразовав, получим выражение одной суммы через другие, меньшей степени.

Если это рекуррентное соотношение выразить для , то мы получим набор чисел, свёртка которых с биномиальными коэффициентами будет равна нулю. Числа Бернулли.

— Выводит все коэффициенты из начального .

Якоб Бернулли получил названные в честь него числа проанализировав закономерности сумм степеней натуральных чисел, суммы прямо выражаются через эти числа.

Представим суммы как числа разложения для функции .

Двойная сумма может быть представлена двумя способами, в зависимости от того, какую из двух сумм убрать, а какую оставить. В начальном виде это просто разложение . А в преобразованном виде это сумма степенной функции, которую можно рассчитать как сумму геометрической прогрессии. Полученное выражение можно разделить на произведение двух функций, и вторую снова представить в виде разложения.

Разложение произведения функций это свёртка их разложений. Получается, суммы это свёртка с биномиальными коэффициентами, числами Бернулли и степенью числа, до которого считаем:

Развёрнутая формула для суммы:

Например

Вот так просто, оказывается, можно суммировать степени натуральных чисел.

По сравнению с интегралом здесь внимание идёт на разделение суммы на отдельные части, каждая с отдельным значением, что, как видно, представляется отдельными составляющими с коэффициентами из чисел Бернулли, начиная со второго. Результат может совпадать. Получается что-то, что можно назвать дискретизацией. Взаимосвязь и .

Откатная функция

Посмотрев на функцию, у которой ряд производных состоит из коэффициентов Бернулли — как она сходится к нулю, и как это обратно отражается на коэффициенты, можно заинтересоваться, как вообще устроена сходимость.

У любой функции, стремящейся к нулю, увеличение аргумента на шаг вперёд уменьшает функцию, и значит, шаг назад увеличивает. Можно задать свойство, что при уменьшении аргумента на единицу значение увеличивается на изначальный аргумент.

Такая функция в нуле и в единице совпадает, и можно приравнять её в этих точках к единице и после этого рассмотреть, какими будут значения в других местах.



Для целых положительных аргументов откат соберёт в одно произведение все промежуточные значения

Для целых отрицательных значение обнулено. Произведение функции и функции от аргумента взятого с обратным знаком из целых аргументов будет отличаться от нуля только в самом нуле.

Одна такая функция, которая из кратных аргументов имела единичное значение только в нуле, у нас уже была, это . И похоже, у нас появилось для неё третье определение.

Из такого равенства много информации о функции не получить:

Но одно новое значение ухватилось:

И для всех полуцелых аргументов могут быть получены тоже.

А как же остальные?

Хорошо, что есть более точное определение:

Сразу видно, при умножении на функцию с обращённым по знаку аргументом знаменатель сокращается, а при нуле и при единице значение функции — один.

Так как факториал может быть представлен через гамма-функцию, , то можно выразить через неё.

Постоянная Эйлера — это предел расхождения между суммой и интегралом , при том, что оба предела не имеют. В произведении у знаменателя в показателе накапливается сумма обратных степеней, общий коэффициент вне произведения прибавляет разницу, превращая это в интеграл. Здесь он встроен так, что полезен, не смотря на то, что расходится. Результат в виде гасит другое расхождение.

А в прямой форме интеграл может, наоборот, не давать сойтись к нулю:

Если заморочиться и совместить закономерности гамма-функции и синуса, то можно вывести прямую формулу с интегралом:

Конечно, — функция комплексная. Вот график её логарифма, демонстрирующий логарифм модуля в реальной части и фазу функции в мнимой.



Расширяя простую закономерность

Получим

Эта штука поинтереснее бинома Ньютона. Можно попробовать раскрыть.

Произведение чисел от одного до становится факториалом. А вот с первой степенью уже чуть сложнее: нужно сложить все варианты произведения, в каждом из которых исключено одно число. Но это тоже можно выразить через факториал.

Со второй степенью так же, суммируются варианты произведение всех скобок, но в каждом варианте две скобки исключены.

Только, общим порядком исключается вариант с совпадением чисел, а его исключать не надо, так как его и нет. Так что, такое исключение тут же само исключается — компенсируется. И затем выражение нужно поделить на два, так как двойная сумма даёт два варианта для одинакового выбора исключаемой скобки, в прямом и в обратном порядке.

Перенесём факториал влево, как общий множитель.

Эта формула похожа на допрос — что ещё можно сказать о функции, кроме того, что по натуральным аргументам она обратна факториалу?

Для лёгкости чтения обозначим суммы степеней как функцию

Для дальнейшего упрощения можно использовать уже известные закономерности:

Константа это средняя пропорция того, что остаётся от факториала, когда из него удаляют по одному множителю, не может быть больше единицы. При увеличении она стремится к нулю, но медленнее, чем возрастет , поэтому возрастает неограниченно.

При независимых параметрах сумма произведения это произведение сумм. Получается, двойная сумма это просто квадрат суммы. Так что можно записать:

Видна взаимосвязь с разложением функции в ряд производных:

С такой подсказкой уже легко подсчитать коэффициенты третьей степени : После расчёта всех вариантов компенсируется три варианта парного повторения, внутри этой компенсации скомпенсирован повтор параметров. И потом компенсируется общий тройной повтор.

Сильно вдумываться в построение коэффициентов не нужно, есть рекуррентная формула:

С раскрытием скобок разобрались. И тут обнаруживается, что это всё было про биномиальный коэффициент:

Особенность в том, что может уйти в бесконечность, а формула останется верной, будет представлена бесконечным рядом коэффициентов.

Сравнивая формулу с предельной формой можно увидеть: в знаменателе левой части и исчезли, будто сократились. Суммы внутри коэффициентов приняли своё предельное значение. При этом с первой суммой произошло что-то особенное: это был стремящийся к нулю коэффициент, умноженный на параметр стремления — и расходящаяся сумма, в виде всё же сошлась, к постоянной Эйлера-Маскерони, . Предельной формой стало .

Это даёт повод предполагать, что при некоторых условиях у предельных форм расходящихся сумм могут существовать определённые значения.

В этих условиях произведение вместо сокращения до сокращается до единицы. То есть, и в рамках аргумента функции отличаются не количественно, а качественно — сумма по результату не отличается от .

Пи

Если выразить число из определения , то получившаяся формула будет аналогична формуле Валлиса:

То же самое можно получить, перекинув в формуле Валлиса первый множитель на противоположную часть равенства и заново переразбив на пары.

Получилось три выражения через бесконечные произведения:

Интересно выглядят их соотношения:

Здесь чётные и нечётные множители в отдельном виде представляют собой .

Число , выраженное по другим определениям :

Можно сравнить с круглым распределением

Функция состоит не только из нулей

Если перемножить , то нули у получившейся функции будут совпадать с нулями самой . И вдобавок появится зависящий от множитель.

Для взаимосвязь будет и общая формула

Похоже, что в этом расширении нули функции ещё и имеют свой вес — когда умножением на добавляется ноль, для аналогичного результата нужно не только сдвинуть функцию, но и умножить её на некоторое число.

Чтобы разобрать на производные, можно отделить константный множитель и оставить множитель с зависимостью от .

При умножении на степенную функцию производная функции меняется и становится:

Если степенной множитель привести к натуральному основанию, то:

Для второй производной зависимость добавляемой части будет и от значения и от первой производной:

— Ещё одно выражение с биномиальными коэффициентами. А когда используется для внесения изменений в разложение — повторяет его рекуррентность. Разложение получается

Добавление параметра отражается на образование -функции:

На синус и косинус повлияло заменой на коэффициент:

Такое же расширение как для функции можно сделать и для гамма-функции:

Тогда балансирует аргумент:

Для того чтобы перейти от к нужно не только обратить функцию, но и ещё сдвинуть аргумент , поэтому полностью сбалансированный вид произведения балансирует и сдвиг аргумента:

Суммируя

Для того чтобы узнать значения для предельных форм расходящихся сумм есть один интересный трюк. Сумма делится на чётные и нечётные слагаемые, образуя как бы две суммы. Затем у суммы составленной из нечётных слагаемых меняется знак.

Если до этого обе суммы могли расходиться, то теперь общим результатом будет их разница, которая при этом имеет возможность сойтись. Разумеется, результат получится другой. Но если между суммами известно соотношение, то по этому результату можно восстановить значение предельной формы исходной суммы.

Таким образом можно получить условное значение бесконечной суммы из степеней натуральных чисел, для всех отрицательных степеней, за исключением . И для соответствующих комплексных степеней тоже. Для удобства знак аргумента изменён. Обозначается такая функция как . И называется Дзета-функция Римана. Например, в точке ноль она имеет значение

Это значение, хотя для его получения и использовалась циклическая сумма, различается с результатом вычисления циклической суммы напрямую, реальная часть там имеет положительный знак и в мнимой части бесконечность. Но всё же, некоторое сходство есть.

Значение равно второму числу Бернулли (с индексом один). Случайное совпадение? Нет, конечно. Все остальные числа Бернулли тоже отражены в функции.

Только, даже по этой формуле у нулевой точки должен был бы быть другой знак.

Зато, все равные нулю числа Бернулли прямо определяют соответствующие нули у Дзета-функции.

Со стороны положительных чисел значение тоже отражает числа Бернулли. Но отражает только не бывающие нулями чётные числа, и чередование знаков чисел скомпенсировано.

А вот эта формула уже даёт для нулевой точки правильное, полученное ранее, значение.



При сравнении двух формул, кроме разного обращения со знаками, разных сомножителей, разного участия значений с нечётными индексами, выявляется ещё одна разница: одна формула за ось берёт единицу, другая формула за ось берёт ноль. Причём, отсчёты идут навстречу друг другу — от нуля в большую сторону, а от единицы в меньшую. Тема противостояния нуля и единицы, поднятая в самом начале статьи, продолжает раскрываться.

Обе точки, ноль и единица, получается, особенные. Область определения функции как бы делится на три части, аргумент с отрицательной реальной частью, реальная часть между нулём и единицей, и реальная часть аргумента больше единицы. Можно сказать, что у функции сразу две оси.

Если бы у -функции нули были бы только в нечётных отрицательных аргументах, она бы совпадала с какой-нибудь из . Но она не совпадает, так что где-то нули точно есть ещё. Интересно, где?

Они не могут располагаться в области , так как в этом случае при сравнении по модулю сумма чётных слагаемых всегда меньше суммы нечётных слагаемых, и образовать ноль они не могут.

В области отрицательной реальной части аргумента можно попробовать компенсировать существующие нули и посмотреть, что останется. Так что, поделим на .

Жаль, этот вариант ничего не показывает: ряд в числителе при отрицательных значениях не сходится, сократить ничего не получится. Что ж. Тогда посмотрим другие определения функции.

Умножая

Сумму из ряда обратных степеней натуральных чисел можно шаг за шагом переложить в произведение с участием простых чисел

Так что у Дзета-функции при реальной части аргумента больше единицы два определения, развёрнутое и свёрнутое — такое, в котором участвуют не натуральные, а простые числа.

Напоминает формулу Валлиса, там , здесь .

Причём, в формула Валлиса частный случай определения , в котором диапазон произведения можно расширить вдвое.

А здесь диапазон расширить сложнее — разве существуют простые числа с отрицательным номером?

Почему в точке дзета-функция нулевая? Видимо, (пусть это и предположение о функции за рамками области определения по выбранной формуле)

Такое произведение всех чисел на единицу меньше простых и всех на единицу больше простых, проявляя безразличие к знаку, явно уходит в абсолютную бесконечность. Не простую, а ту которая делится на всё что угодно. Все чётные отрицательные аргументы дзета-функции тоже приводят к нулю, ведь, по совпадению, всё то же самое верно для любой натуральной степени простых чисел. Тривиальные нули дзета-функции не такие уж и тривиальные. Какие же тогда остальные?

Интересный, кстати, вопрос: что точнее, или ? С одной стороны, возведение двойки в положительное число обычно больше, чем это число, а с другой стороны, получившееся число не делится на три, да и на другие простые числа. Так что его до настоящей бесконечности ещё умножать и умножать. Кажется, знаменитый математик Эскобар на полях книги заметил, что решил это задачу, но не пояснил как.

Симметрия Дзеты

Здесь позволю себе брать формулы напрямую из статьи Римана. Подобно тому как откатная функция имеет определение через интеграл, Дзета-функция Римана тоже такое имеет, и очень похожее.

Как снова не вспомнить про числа Бернулли — под интегралом находится образующая их функция, с небольшим добавлением параметра. Похоже, не все нули при умножении на интеграл остаются нулями. Впрочем, область определения ограничена.

А дальше Риман обобщает, выводит

Вы, может быть, раньше думали, что одинаковые пределы интегрирования не используются? А как на счёт найти разницу интегралов от нуля до бесконечности по обе стороны нулевой мнимости ?

Риман это сделал запросто.

Спустя буквально один абзац объяснений про то как интегрировать при отрицательном аргументе у него появляется запись

А тут уже две Дзета-функции. Одна от , другая от .

В следующей строчке своей статьи (в моём пересказе) Риман замечает: отсюда со всей очевидностью следует, что

После этого вывести «функциональное уравнение» остаётся делом техники. Оказывается, есть симметричная форма, Кси-функция.

По этому равенству видно: если взять симметричную форму, понавтыкать нулей в чётных отрицательных аргументах, добавить полюс в единицу и умножить на корень из в степени аргумента, то получится обычная несимметричная форма Дзета-функции.

В области в симметричной форме столько же нулей, как в области — их нет. Так что, теперь ясно, что при отрицательной реальной части встречаются только тривиальные нули. Осталось разобраться с полоской между нулём и единицей.

Ось

Для получения значений на полосе достаточно простого суммирования

Рассматривая изменения комплексного значения на оси этой полоски можно увидеть, что оно сначала проходит мимо ноля, разворачивается, идёт дугой и чётко по нему попадает. Обходит сбоку и опять попадает, и потом ещё и ещё. Какая-то мания проходить ноль меняя мнимость только в одном направлении. При этом расстояние при обходе и угол захода варьируются в широких пределах.

Отдельно фаза этого перемещения:



У симметричной формы у расположенных на оси значений нет мнимой составляющей. Мы можем из коэффициента для получения симметричной формы взять только фазу, компенсировать фазу у Дзета-функции, и всё: никакого вращения, только колебания вверх-вниз.



Так что, эта мания — это стремление вернуться на другую сторону модуля при том что фаза переключается примерно с той же скоростью, только равномернее. Я бы поделил все нули на чередующиеся «восходящие» и «нисходящие». Тогда у функции стало бы три типа нулей.

Откуда там вообще нули?

Если выразить Дзета-функцию через интеграл с выделением оси, то получится

Интеграл, в котором присутствуют колебания с логарифмической зависимостью фазы от , с определением модуля через пару множителей.

Поделив на два диапазона

И применив закономерность выворота диапазона интеграла наизнанку

Получим равенство

Почему бы теперь начало диапазона снова не сделать нулём, ввернув вместо его экспоненту, и скомпенсировав равномерность интеграла коэффициентом.

Выравнивающий коэффициент это просто , поэтому норма — уровень, оказывающий одинаковое влияние на значение интеграла — это спадающая экспонента .

Визуальное сравнение коэффициентов:


После нормировки:



Один множитель с возрастанием гасится, становится меньше нормы, другой возрастает, и чем дальше тем больше. Под интегралом оба слагаемых имеют множители равномерного колебания, с частотой, определяемой аргументом , только у разных множителей различный знак частоты, и их значения комплексно-сопряжённые. Если бы не колебательные множители, интеграл бы расходился. Да он и расходится. Значение Дзета-функции при отсутствии колебаний , говорит об отрицательном значении интеграла, состоящего из положительных значений.

Интегралы с колебательным множителем аналогичны преобразованию Фурье. А в преобразовании Фурье, как было замечено в статье про волны, если проигнорировать расхождение интеграла, переполнение одной комплексной составляющей может влиять на другую комплексную составляющую. Здесь, видимо, хорошее такое переполнение — влияние идёт на саму же составляющую в обратную сторону.

После упрощения

Равенство напоминает уравнение симметрии.

С заменой развёртки дроби для получения троллинг-формулы на взятие интеграла. Стоит выделить главное отличие: интеграл позволяет подынтегральным слагаемым не быть нулевыми при нулевом общем значении.

При интегрировании множитель, вносящий колебания в каждое слагаемое, циклически сворачивает значения: нечётный полупериод такого цикла уменьшает величину, выросшую на чётном полупериоде. Только, как в нормальной троллинг-формуле, один из двух интегралов даже не смотря на это не сходится. Или сходится, но к каким-то непредсказуемым величинам.

Оба интеграла можно объединить в один

Вот это да! Что это за фокусы? Неожиданно для меня самого. Интегралы оказались равны:

И для этого вовсе не обязательно . Получилось ещё одно выражение для симметрии Дзета-функции. Я хотел получить хотя бы один нетривиальный ноль, с точным объяснением почему он такой.

— Получилось только это симпатичное равенство. Всё что оно показывает — что в интеграле, похожем на преобразование Фурье некоторой функции, для выбранной частоты, задаваемой мнимой частью , отрицательный и положительный диапазоны интеграла иногда могут компенсировать друг друга.

Давайте посмотрим на эту функцию.



— Функция, которая раскладывается на частоты. Результат деления на совсем немного отличается от . При проверке эта разница после преобразования Фурье и умножения на соответствует дзета-функции на оси. Видимо, у функции преобразование Фурье нулевое, и на результате отражается только разница.

А так сразу и не скажешь, что у этого бугорка выпадают частоты.

После небольшого обобщения получится, что когда в появляется реальная составляющая, то функция вместе с балансирующим слагаемым становится

Если у вас возникает вопрос, может ли при ненулевой сигме из такой функции выпасть частота, то вы не одиноки. Никто не может ответить, почему нет.

Логарифм бугорка в комплексном пространстве выглядит так:




Причём, он периодичен по мнимой составляющей аргумента. У модуля , у фазы .

Похоже на шнуровку ботинка:



Светлые точки соответствуют нулевому знаменателю первого слагаемого.

Тёмные точки соответствуют суммированию слагаемых в ноль.

По графику видно, что при сдвиге аргумента в мнимую сторону на компенсация перестаёт срабатывать, и компенсированный вид со сдвигом аргумента аналогичен нескомпенсированному без сдвига. Возможно, что у балансирующего слагаемого есть более полная форма, сохраняющая интеграл и при изменении знака у . Вот бы её тоже найти.

---

Числа скучные — статья развлекательная. Вместо рекламы здесь указание на существование возможности доната.