
Кадр из мультфильма «Over the Garden Wall» (2014)
Большое количество курсов по аналитике данных и питону создает впечатление, что «два месяца курсов, пандас в руках» и ты data science специалист, готовый порвать любую прямоугольную задачу.
Однако, изначально просто счёт относился к computer science, а data science было более широким и междисциплинарным понятием. В классическом понимании data scientist — «T-shape» специалист, который оцифровывает и увязывает административные и предметные вертикали/горизонтали компаний через математические модели.
Далее немного иллюстрирующих примеров.
Является продолжением серии предыдущих публикаций.
Задачки
Упомянем большую часть используемых ниже библиотек.
library(tidyverse)
library(lubridate)
library(magrittr)
library(akima)
library(data.table)
library(igraph)
library(stringi)Формирование иерархического списка работ
Задачка является классической в тематике управления проектами. Есть записи по выполненным работам в виде
Проектирование - Фаза 1 - Модуль А
Проектирование - Фаза 1 - Модуль Б
Релизация - Фаза 1 - Модуль А
Релизация - Фаза 2 - Модуль Б с дополнительным атрибутарным наполнением этих работ. Требуется построить иерархическую схему
WBS (Work breakdown structure). Т.е. создать прямоугольное представление со всеми этапами и подэтапами, как они встречаются в работах и с формированием цифровых иерархических идентификаторов для каждого элемента.

Вариант решения «в лоб»
Классический data.frame/pandas подход, который предлагают в первую очередь, на первый взгляд может показаться логичным и красивым.

df <- tibble(element = str_c("el", c(1, 1, 2, 2, 3)),
sublvl = str_c("obj", c(1, 2, 1, 1, 1)),
value = str_c("val", c(1, 1, 1, 2, 1)))
df %>%
mutate(across(everything(), parse_number, .names = "{.col}_num")) %>%
pivot_longer(cols = element:value, names_to = "type") %>%
mutate(id = case_when(
type == "element" ~ as.character(element_num),
type == "sublvl" ~ str_c(element_num, sublvl_num, sep = "."),
type == "value" ~ str_c(element_num, sublvl_num, value_num, sep = ".")
)) %>%
select(id, value, type)Но забыта одна маленькая вещь. Нумерация записей el1, el2… привнесена нами самостоятельно на этапе постановки задачи для большей ясности. Но в рельных планах работ такого не будет. Будут "Заливка бетона", "Разработка интеграционного адаптера", "Инструктаж" и т.д. И весь красивый концепт на парсинге и номеров проваливается. Да и текстовая иерархия не собрана.
Альтернативный вариант
Попробуем посмотреть на задачу иным образом. Один из способов — генерация графа (дерево является частным случаем) и анализ путей по графам для каждого терминального элемента. Можно, но будет не то чтобы просто.
Но есть и другой вариант.
Все это очень сильно напоминает автоматическую нумерацию заголовков при верстке текста. А точнее, это все идентично механизму нумерации заголовков в LaTeX, который там элегантно реализован через семейство иерархических счетчиков. Воспользуемся этим решением.
plain_df <- tribble(
~element, ~sublvl, ~value,
"el1", "obj1", "val1",
"el1", "obj2", "val1",
"el2", "obj1", "val1",
"el2", "obj1", "val2",
"el3", "obj1", "val1",
"el1", "obj1", "val3"
)
toc_dt <- plain_df %>%
rename(val1 = element, val2 = sublvl, val3 = value) %>%
# формируем счетчики заголовков (TOC_counter)
as.data.table() %>%
.[, idx := .I] %>%
.[, cnt1 := rleid(val1)] %>%
.[, cnt2 := rleid(val2), by = cnt1] %>%
.[, cnt3 := rowidv(val3), by = .(cnt1, cnt2)] %>%
# формируем все возможные комбинации оглавлений по иерархии
.[, {list(toc_num = c(cnt1,
paste(cnt1, cnt2, sep = "."),
paste(cnt1, cnt2, cnt3, sep = ".")),
toc_name = c(val1,
paste(val1, val2, sep = "."),
paste(val1, val2, val3, sep = ".")))}, by = idx] %>%
# оставляем только первое вхождение для каждого элемента оглавления
.[, head(.SD, 1), by = toc_num]
as_tibble(toc_dt)Получаем результат
# A tibble: 14 x 3
toc_num idx toc_name
<chr> <int> <chr>
1 1 1 el1
2 1.1 1 el1.obj1
3 1.1.1 1 el1.obj1.val1
4 1.2 2 el1.obj2
5 1.2.1 2 el1.obj2.val1
6 2 3 el2
7 2.1 3 el2.obj1
8 2.1.1 3 el2.obj1.val1
9 3 5 el3
10 3.1 5 el3.obj1
11 3.1.1 5 el3.obj1.val1
12 4 6 el1
13 4.1 6 el1.obj1
14 4.1.1 6 el1.obj1.val3Сшивка цепочек идентификаторов
Имеется фрейм в котором идет сопоставление идентификаторов id_1 и id_2, причем идут они в случайном порядке. Как можно это сделать?)
id_1 id_2
1 91 8213708
2 8802224 8213708
3 91 123764
4 123764 198237Требуется «выдернуть» меньший id и к нему присоединить все связанные.
id_1 id_2
1 91 8213708
2 91 8802224
3 91 123764
4 91 198237Вариант решения «в лоб»
Специфика задачи такова, что связи могут быть длинными, надо вытаскивать всех «друзей друзей». На примере это видно на идентификаторе 8802224, который напрямую не связан с идентификатором 91.
Какие обычно возникают мысли. Конечно же циклы или рекурсии с джойнами, при этом придется обрабатывать каждую строчку отдельно, поскольку неизвестно отношение между этими друзьями. Все что нам известно — привязываем к минимальному идентификатору (пример задачки — идентификаторы посылок при их консолидации или передаче партнерам).
Код с этими экспериментами приводить не буду — будет много и некрасиво. Важно учесть, что в реальной задаче число таких записей измеряется десятками миллионов.
Альтернативный вариант
Посмотрим на эту задачку с высоты птичьего полета. Что это напоминает? Да это же описание ребер графа!
И тогда задачка сводится к задаче связности, а именно к поиску всех нод, которые связаны с интересующей нас. Имеем одну строчку кода.
df <- data.frame(
from = c(91, 8802224, 91, 123764),
to = c(8213708, 8213708, 123764, 198237)
)
gr <- igraph::graph_from_data_frame(df, directed = FALSE)
plot(gr)
# достанем все ноды, которые доступны от заданной
igraph::dfs(gr, root = "91", unreachable = FALSE)$orderОтвет и графическая иллюстрация
+ 5/5 vertices, named, from adf663b:
[1] 91 123764 198237 8213708 8802224
Треугольная матрица
Существует функция $f(x,y)$ симметричная относительно перестановки $x$ и $y$, которую необходимо посчитать по очень мелкой сетке. Мелкой настолько, что время счета и объем этой матрицы становятся критичными. Самый тривиальный пример — сила притяжения между двумя объектами.
ff <- function(i, j){
sqrt(i^2 + j^2)
}Вариант решения «в лоб»
Будем считать функцию только для треугольной матрицу. Сэкономим лишь на времени вычисления, но не на памяти.
n_max <- 7
mm_v1 <- matrix(nrow = n_max, ncol = n_max)
for (i in 1:n_max){
for (j in 1:i){
# cat(paste0(i, ':', j, '\n'))
mm_v1[i, j] <- ff(i, j)
}
}Казалось бы, что это вполне неплохой результат. Но он таит один серьезный подвох. Если $f(x, y)$ достаточно сложная, а матрица большая, то время расчетов может составлять часы и дни. Попытка вручную распараллелить подобные вычисления может потерперь фиаско — сложно нарезать сбалансированные блоки для вычислителей, а отдельные языки, обладающие нужным функционалом под капотом, испытывают проблемы при оптимизации внутренней механики параллелизации.
Альтернативный вариант
Если посмотреть на эту задачу немного под другим углом, то вся «треугольность» матрицы окажется несколько надуманной. По сути, это просто контейнер для значений функции с хитрой двухпозиционной адресацией. Т.е. все это можно превратить в линейный массив (один непрерывный кусок памяти) со значениями функции с функцией разложения индекса массива на исходные $x$, $y$, требуемые для расчета функции.
Как это можно сделать? Да очень просто, мы имеем дело с тривиальной арифмитической прогрессией с шагом 1 и начальным значением 1.
$i$ — номер колонки, $j$ — номер строки, «треугольная» матрица пусть выглядит таким образом.
## X1 X2 X3 X4 X5
## [1,] "*" " " " " " " " "
## [2,] "*" "*" " " " " " "
## [3,] "*" "*" "*" " " " "
## [4,] "*" "*" "*" "*" " "
## [5,] "*" "*" "*" "*" "*"Тогда номер индекса (количество ячеек от начала) будет выражаться формулой.
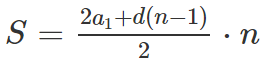
Приземляем на наши параметры, получаем $(j + 1) \cdot j = 2 S$.
Сделав подстановку $j = k — 1/2$ получаем $k^2 — 1/4 = 2S$.
$j$ составит целую часть корня, $i$ — остаток.
reIndex <- function(idx){
# можем и округлять
j <- as.integer(sqrt(2* idx + .25) - .5)
S <- j * (j + 1)/2
i = idx - S
if (i == 0) {
# попали в полное число полосок
i <- j
} else {
# строку уводим на полоску ниже, которая догоняется кусочком i
j <- j + 1
}
list(i = i, j = j)
}
mm_v2 <- matrix(nrow = n_max, ncol = n_max)
for(i in 1: (n_max * (n_max + 1) / 2)){
pt <- reIndex(i)
i <- pt$i
j <- pt$j
mm_v2[j, i] <- ff(i, j)
}
waldo::compare(mm_v1, mm_v2)Матрица в альтернативном варианте формируется исключительно для сравнения результатов. Но, если есть немного памяти, то можно задачу упростить еще сильнее. Идея в том, что мы генерируем полное представление индексов для итерирования и потом формуем его под нашу задачу. Получаем линейный массив, который потом хорошо отдается на параллельные вычисления. Фактически, формируем список заданий на вычисление, не обязательно «треугольное», можно и с вычетами.
df <- 1:10 %>%
{tidyr::expand_grid(i = ., j = .)} %>%
filter(i <= j) %>%
mutate(val = ff(i, j))Манипуляции с прямоугольными представлениями
Очень типичная задача, когда нужно провести некоторые линейные трансформации и с данными. И ведь вроде простая задача, но всегда можно копнуть чуть глубже.
Есть два вектора
c("1", "2", "3", "4")
c("a", "b", "c", "d")нужно получить
c("1", "a", "2", "b", "3", "c", "4", "d")Можно ли это сделать без циклов?
Вариант решения «в лоб»
Если не использовать циклы (сознательно пропустим это упражнение), то руки и память тут же подсовывает итераторы. Круто, но по своей сути это цикл, спущенный на уровень ниже. Способ решения задачи при этом никак не меняется. Манипуляции с памятью остаются в накладных. Кручу-верчу, вектор собрать хочу.
unlist(purrr::map2(
c('1', '2', '3', '4'),
c('a', 'b', 'c', 'd'),
function(x, y) c(x, y))
)Альтернативный вариант
Опустимся на железный уровень и вспомним, что такое массив и матрица и чем они отличаются от data.frame. Все просто. Массив и матрица — единый кусок памяти, запрошенный у ОС + атрибуты размерности + быстрый доступ к ячейке памяти по смещению от начала.data.frame — список указателей на массивы. Очевидно, что манипуляция с последним куда накладнее.
И вот получается альтернативное решение, если кто знает еще проще — пишите. Конструируем матрицу по горизонтали, собираем урожай по вертикали.

Квадратно-гнездовой метод посадки (аналогия из сельского хозяйства), прямой менеджмент памяти, (пандас, привет!).
a <- c('1', '2', '3', '4')
b <- c('a', 'b', 'c', 'd')
m <- matrix(c(a, b), nrow = 2, byrow = TRUE)
c(m)Подготовка time-series
Есть time series, содержащий данные сигналов с датчика влажности воздуха (время сигнала и влажность соответственно). Между сигналами в среднем 5 минут. Требуется вставить строки, если между сигналами больше 5 минут, причем строк нужно вставить столько, сколько кратно 5 минутому разрыву (т.е. разрыв в сигналах 16 минут требует вставки 3-х строк).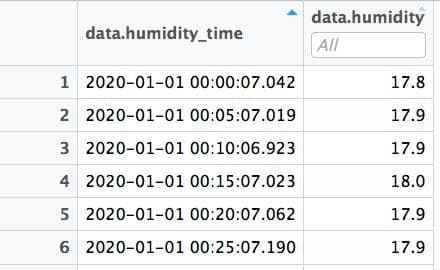
Вариант решения «в лоб»
Самый популярный вариант — вставка через циклы. Более элегантный вариант — попробовать притянуть различные пакеты для time-series, например функции pad_by_time, fill_gaps и т.д.
Какой-то результат можно получить, но это все грубо и некрасиво.
Следующий шаг — затащить артиллерию ML и начать говорить о missing data imputation с применение деревьев или еще чего-нибудь. Круто это все! Но может можно спуститься на землю?
Альтернативный вариант
Какие есть соображения?
- Опустимся на предметную область. Датчик влажности — вещь из физического мира. У него есть определенная инерционность и у среды, в которую он помещен, также эта инерционность есть. Почва это или помещение, в любом случае, 5 минут — много меньше характерного периода изменения влажности. Мы можем пропустить несколько периодов времени, но если уж пошел ливень, то сыро будет долго — все равно нам показания достанутся.
- Задачу надо переформулировать. Нам не вставку данных абы куда надо сделать, а привести к регулярной сетке с шагом в 5 минут. Регулярная сетка пригодится для множества последующих шагов.
Однако, некорректно делать округление времени, ошибки могут оказаться очень значимыми, особенно на производных.
Что делать? Да все давно уже придумано. Можно воспользоваться интерполяцией существующей точки сплайнами (привет, Corel Draw и Adobe Illustrator) по сформированной вручную регулярной сетке. Причем, в зависимости от предметной области, можно делать интерполяцию CDF, а потом считать производную.
library(tidyverse)
library(lubridate)
library(magrittr)
library(akima)
# создадим тестовый набор данных
time_grid <- seq(as.POSIXct("2021-05-01 8:00:00"),
as.POSIXct("2021-05-01 12:00:00"), by = "5 min")
df <- tibble(timestamp = time_grid) %>%
mutate(timestamp = timestamp + runif(n(), -1, 1),
value = rnorm(n(), mean = 20, sd = 5)) %>%
sample_frac(.6)
grid_df <- aspline(x = df$timestamp, y = df$value,
xout = time_grid, method = "original") %$%
tibble(timestamp = x, value = y)
ggplot(grid_df, aes(timestamp, value)) +
geom_point(data = df, colour = "blue", size = 4) +
geom_line() +
geom_point(colour = "red") +
theme_minimal()
В рамках альтернативного пути возникает еще несколько дорожек.
-
Для очистки регулярного time-series хорошо использовать методы и алгоритмы из цифровой обработки данных (DSP), в частности частотные фильтры с применением преобразования Фурье.
-
Можно time-series трансформировать так, что частота дискретизации подпадает под 44кГц — для всяких преобразований и фильтраций можно воспользоваться софтом для редактирования аудио (Audacity, например, или же коммерческое ПО). Масса всяких фильтров и трансформаций, как во временнОм представлении, так и в частотном. Визуальное представление результатов операций. Удобно. Популярный time-series по продажам товаров вполне неплохо трансформируются на шкалу 44 кГц.

Если уж идти дальше по такому пути, то и графические редакторы иногда бывают удобны для прототипирования визуализации. Механизм слоев позволяет визуально покрутить различные наложения, особенно в случае сложного пересечения тепловых карт или наложения на геоподложки. Не обязательно все крутить в стеке DS.
Комбинаторные задачки
Рассмотрим на примере школьной задачки, не погружаясь в enterprise пучины.
В заборе 7 досок. Каждую доску надо покрасить в один из 4-х цветов, причём соседние доски должны быть покрашены в разные цвета. Сколькими способами это можно сделать?

Вариант решения «в лоб»
Понятно, что эта задачка на комбинаторику. Но подобные задачки встречаются часто и в программировании. И тут начинаются страшные огороды. Можно использовать метод Монте-Карло для генерации комбинаций и потом попарно сравнивать элементы, с целью исключения запрещенных комбинаций. Семь досок, еще куда ни шло, можно написать все сравнения. 1 и 2, 2 и 3, 3 и 4 и т.д.
В лучшем случае что-то подобное.
library(tidyverse)
library(stringi)
df <- as.character(1:4) %>%
tidyr::crossing(d1 = ., d2 = ., d3 = ., d4 = ., d5 = ., d6 = ., d7 = .) %>%
filter(d1 != d2, d2 != d3, d3 != d4, d4 != d5, d5 != d6, d6 != d7)Конкретно в этой детской задаче решение выглядит компактным.
Но как поступать, когда этих досок 100+ или вообще неопределенное число?
Начинают предлагать итераторы, анонимные функции, вложенные циклы и т.д.
Тяжко, трудоемко и медленно!
Альтернативный вариант
- Очень нудно загонять все вручную в колонки. Иногда бывает неплохо посмотреть документацию и найти интересные функции, избавляющие от рутины.
purrr::cross(), например, вообще никому не известен. А зря. - Ну хорошо, сейчас сравниваем соседей. А потом надо через одну доску или через две… и их сотни… Что можно сделать? Да ведь у нас есть уже подобный механизм поиска — это регулярные выражения. Да-да, кодируем все в текст и пишем магическую фразу для движка регэкспов.
library(tidyverse)
library(stringi)
dt <- 1:7 %>%
purrr::map(~1:4) %>%
purrr::cross() %>%
data.table::rbindlist() %>%
.[, idx := .I] %>%
.[, .(set = stri_c(.SD, collapse = "")), by = idx] %>%
.[stri_detect_regex(set, r"((.)\1)") == FALSE]library(magrittr)
library(stringi)
wall <- 1:7 %>%
purrr::map(~1:4) %>%
purrr::cross() %>%
purrr::map_chr(stri_c, collapse = "") %>%
.[! stri_detect_regex(., r"((.)\1)")]Механизм перевода в текст и подключения регулярных выражений часто позволяет свернуть страницы мозголомного кода с ошибками свернуть в одну-две строки поиска по регуляркам. Используем модную конструкцию r"(...)
Числовая аннигиляция
Простая задача по наведению порядка в датафрейме.
Есть миллионы чисел в списке. Из этого списка нужно найти и исключать пары чисел $a$ и $b$, такие чтобы $a = -b$.
-1, 1, -2, -2, 2, -3, 3, 3, 3, -4, -4, 4, 4, 4
Вариант решения «в лоб»
Тут встречаются два варианта.
Первый — цикл в цикле. Два бегущих указателя, начинаем сравнивать каждое с каждым и исключать пары. О скорости и говорить нечего.
Второй — построить матрицу, аналогично матрице расстояний. Для десятка чисел может и ок, но для миллионов — полная тоска.
Альтернативный вариант
Вспомним детскую обучающую игру — взвешивание цифр.

По сути нам надо искать антиподов — одинаковый модуль, разный знак. Вот и будем «развешивать» разнознаковые числа на разные плечи весов. Что это означает в переводе на алгоритм? Считаем расстояние от 0 (ищем антиподов), поглощаем их с помощью суммы по группам удаленности. Всего две строки кода.
library(data.table)
dt <- as.integer(c(-1, 1, -2, -2, 2, -3, 3, 3, 3, -4, -4, 4, 4, 4)) %>%
data.table(num = .)
dropDups <- function(dt) {
# считаем расстояние от 0 (ищем антиподов),
# поглощаем их с помощью суммы по группам удаленности
# считаем количество таких непарных элементов, тут ведь как рычажные весы с грузиками
enum_dt <- dt[, dist := abs(num)][, .(n = sum(num)/dist), by = dist][n != 0]
# теперь разворачиваем
enum_dt[, .(val = rep.int(dist * sign(n), times = abs(n))), by = dist]
}
bench::mark(dropDups(dt))Парсинг полуструктурированного csv
Все мечтают получать на вход чистые прямоугольные данные. Но, как правило, приезжает вечно всякая ерунда. И начинаются всякие мучения по парсингу и последующему преобразованию в широкое/длинное представление, группировку/разгруппировку. Разве что данные изолентой не скручивают. Особо досадно бывает, когда данные вроде локально и структурированы, но глобально они свалены в кучу.
Вот типичный пример. Отлично, вроде как csv, только на этапе выгрузки перемешали строки из различных колонок. Никакой парсер съесть это не может.
input_text <- c("
cheсk;store;customer;
product_name;;count;product_price
3282;1 Маркса склад основной;1 Розничный покупатель;
NB 574, Хаки (44);;1;3600
Штаны Yeezy, Бежевый (S);;1;1900
Носки Champion Low;;1;100
NB 997 Sport, Бежевый Серый (42);;1;3300
Толстовка J, Серый (S);;1;1700
3335;1 Маркса склад основной;1 Розничный покупатель;
Подвеска Cactus Jack Cross;;1;500
Носки KAWS XX;;1;200
3384;1 Маркса склад основной;1 Розничный покупатель;
AF1 High, Черный (37);;1;3800
Носки Carhartt;;1;100
3263;1 Маркса склад основной;1 Розничный покупатель;
AF1 Low, Зеленый Белый (45);;1;3900
Футболка Н, Серый (XXL);;1;1100
3596;1 Маркса склад основной;1 Розничный покупатель;
LF1 Duckboot 16, Коричневый Черный (46);;1;4400
3645;1 Маркса склад основной;1 Розничный покупатель;
Носки Н High;;1;200
AF1 Low, Белый (37);;1;3900
3501;1 Гоголя склад основной;Продавец 1;
Патч, S.I.;;1;100
3457;1 Гоголя склад основной;1 Розничный покупатель;
M2K Tekno, Черный Белый (41);;1;3900
3631;1 Маркса склад основной;1 Розничный покупатель;
Носки JORDAN;;1;100
Джоггеры Sea Air, Черный (XL);;1;2500
Носки А Low;;1;100
Носки Авокадо Low;;1;100
Носки ASSC Высокие;;1;100
Носки Happy Socks;;1;100"
)Вариант решения «в лоб»
Взять Excel и руками привести файл в порядок. Выгрузку изменить нельзя, хорошо, что она есть хоть в таком виде.
Альтернативный вариант
Зададимся рядом вопросов.
- Кто сказал, что надо сразу гнать парсер?
- Почему мы не можем рассматривать данные как текст или частичный текст?
- Кто сказал, что парсер можно использовать только однократно?
Остановились, выдохнули, подумали.
Оказывается задача пустяковая, все решается в несколько строк (а выгрузка там немаленькая и регулярная). И не нужны разрабы, админы, базовики и прочие.
# считываем сырье и формируем предварительную табличку на разбор
raw_dt <- input_text %>%
readr::read_lines(skip = 3, locale = locale(encoding = "windows-1251")) %>%
tibble::enframe(name = NULL) %>%
setDT()
temp_dt <- raw_dt %>%
# расставляем маркеры начала записей по якорным словам
.[, line_start := stri_detect_regex(value,
pattern = "склад")] %>%
.[, idx := cumsum(line_start)] %>%
# разделяем на колонки и заполняем пустоты (делаем прямоугольное представление)
.[line_start == TRUE, part1 := value] %>%
.[line_start == FALSE, part2 := value] %>%
# для быстрой проливки строк можно делать группировки, locf и пр.
# выберем вариант data.table, проливаем первую строку по группам
.[, part1 := head(part1, 1), by = idx] %>%
# забираем только полезные данные
.[!is.na(part2)] %>%
.[, data := stri_join(part1, part2)]
# отправляем повторно на штатный парсер csv
df <- stri_c(temp_dt$data, collapse = "\n") %>%
readr::read_delim(
delim = ";",
col_names = c("cheсk", "store", "customer", "product_name", "none", "count", "product_price")
)
Еще немного задачек
В предыдущих публикациях проскакивали примеры подобного плана, дам просто списком:
- «R, Монте-Карло и enterprise задачи, часть 2»
- «Дети, математика и R»
- «R Markdown. Как сделать отчет в условиях неопределенности?»
- «'Оч.умелые ручки': делаем Tableau/Qlik из R и 'синей изоленты'»
Заключение
Примеров можно приводить множество, стоит только немного посмотреть по сторонам. Очень часто оказывается, что наточить пилу и топор куда полезнее и эффективнее, чем безудержно махать, вырабатывая нормочасы.
Предыдущая публикация — «process mining: 100 строк кода и генератор логов у нас в руках».


folal
Пытаюсь понять, при чем здесь хаб python?
i_shutov Автор
Что именно Вам непонятно? Попробуйте сформулировать мысль более конкретно и содержательно. Например, "я прочитал все и в п. X технические нюансы, которые касались R неприменимы в питоне, если используется такая то библиотека..."