"Генерация случайных чисел слишком важна, чтобы оставлять ее на волю случая" - Роберт Р. Кавью

Как-то поздним летним вечером мне пришлось разобраться, как устроены генераторы случайных чисел в Windows и Linux. Собственно, в этой статье я попробую привести саккумулированную информацию, и преподнести ее максимально простыми словами, без необходимости лезть в исходники, туториалы и статьи.

Генераторы псевдослучайных чисел

С развитием технологий и безопасности мы все больше и больше нуждаемся в действительно случайных числах, которые нельзя было бы предсказать извне. Почему? В первую очередь из-за шифрования, ведь с каждым годом растет количество пересылаемого трафика, и при этом хочется иметь достаточную степень безопасности наших данных. И вот в тот момент, когда нужно сгенерировать случайное число, у наших компьютеров возникают проблемы, поскольку они созданы быть максимально послушными, предсказуемыми и детерминированными для того, чтобы все результаты при одинаковых входных данных воспроизводились, иначе бы весь мир развалился.

Выход из данной ситуации нашелся и достаточно изящный - а давайте возьмем "предсказуемый" генератор псевдослучайных чисел (ГПСЧ) и будем его инициализировать случайными битами(пока не задумываемся откуда и как взятыми). Из небольшого числа действительно случайных событий мы сможем получить достаточно хорошие случайные числа в большом количестве. И пока "злоумышленник" не имеет доступа к внутреннему состоянию нашего компьютера, можно полагаться на сгенерированные последовательности таких чисел. Или же можно контролировать количество выданных бит и не позволять отдавать больше энтропии, чем есть в инициализирующем состоянии, тогда предсказать следующий бит будет невозможно.

Генератор псевдослучайных чисел - это функция, которая перемешивает входные биты, применяя к ним простые операции несколько раз, выдает наружу результат, который и является последовательностью случайных бит. Для примера рассмотрим алгоритм ChaCha20, применяемый в Linux, и SP800-90 AES-CTR-DRBG в Windows

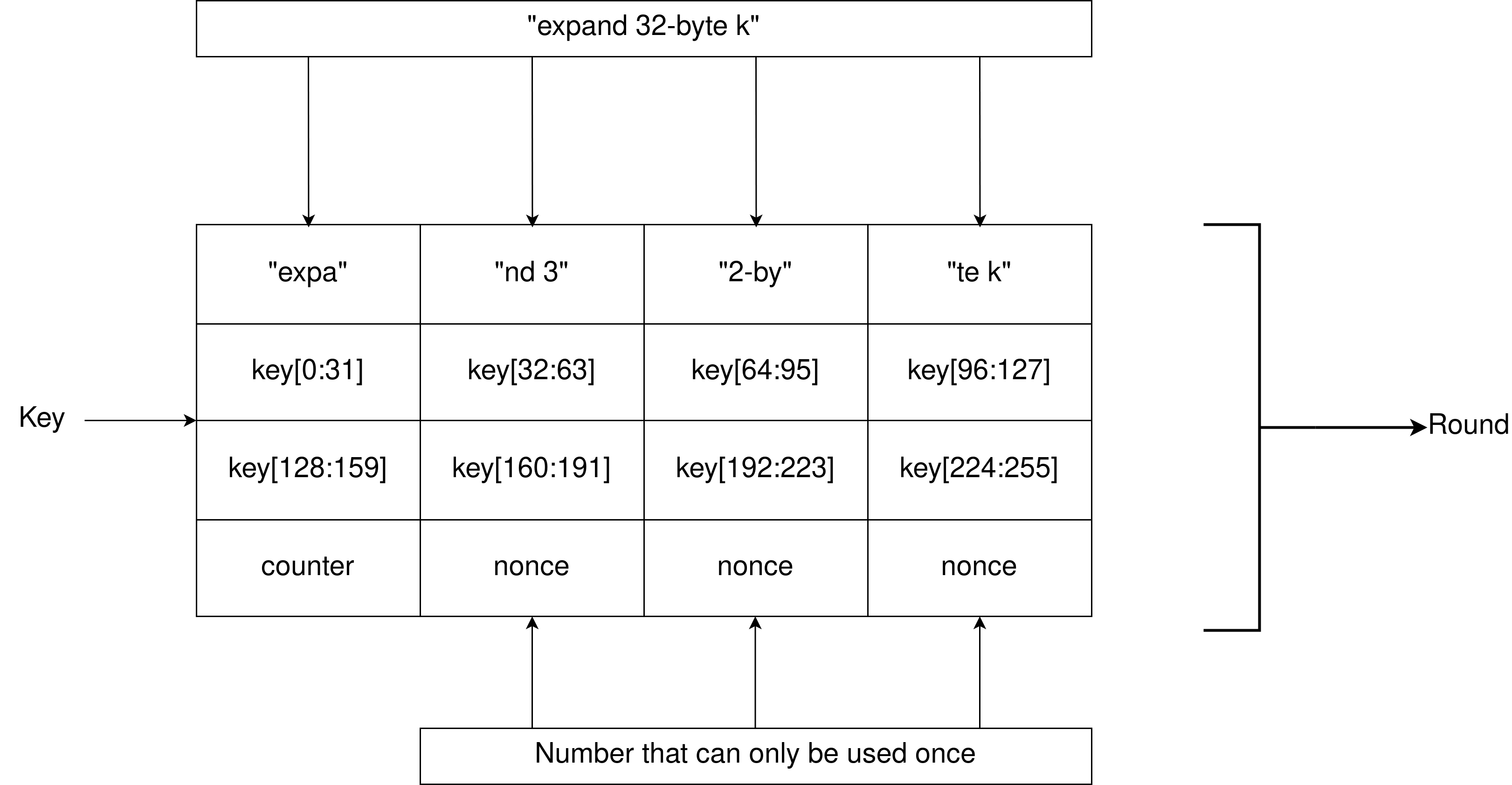
• ChaCha20 - это развитие алгоритма Salsa20. Он основан на комбинации операций: 32-битное сложение, XOR и побитовое вращение. Если кратко: матрица 4 * 4 заполняется особой константой, ключом, счетчиком и одноразовым числом для текущей итерации, а затем происходит перемешивание бит в течение 20 раундов алгоритма. При этом нечетные раунды отвечают за изменения бит по столбцам матрицы, а четные за изменения по диагоналям. Полученные на выходе биты и есть псевдослучайное число, которое к тому же является входным состоянием для следующего запуска генератора. Но, так как при таком подходе было бы очень легко предсказать все следующие числа, существует обязательная операция изменения ключа после каждого запроса;

// linux/lib/crypto/chacha.c
for (i = 0; i < nrounds; i += 2) {
// Odd round
    x[0]  += x[4];    x[12] = rol32(x[12] ^ x[0],  16);
    x[1]  += x[5];    x[13] = rol32(x[13] ^ x[1],  16);
    x[2]  += x[6];    x[14] = rol32(x[14] ^ x[2],  16);
    x[3]  += x[7];    x[15] = rol32(x[15] ^ x[3],  16);

    x[8]  += x[12];   x[4]  = rol32(x[4]  ^ x[8],  12);
    x[9]  += x[13];   x[5]  = rol32(x[5]  ^ x[9],  12);
    x[10] += x[14];   x[6]  = rol32(x[6]  ^ x[10], 12);
    x[11] += x[15];   x[7]  = rol32(x[7]  ^ x[11], 12);

    x[0]  += x[4];    x[12] = rol32(x[12] ^ x[0],   8);
    x[1]  += x[5];    x[13] = rol32(x[13] ^ x[1],   8);
    x[2]  += x[6];    x[14] = rol32(x[14] ^ x[2],   8);
    x[3]  += x[7];    x[15] = rol32(x[15] ^ x[3],   8);

    x[8]  += x[12];   x[4]  = rol32(x[4]  ^ x[8],   7);
    x[9]  += x[13];   x[5]  = rol32(x[5]  ^ x[9],   7);
    x[10] += x[14];   x[6]  = rol32(x[6]  ^ x[10],  7);
    x[11] += x[15];   x[7]  = rol32(x[7]  ^ x[11],  7);
// Even round
    x[0]  += x[5];    x[15] = rol32(x[15] ^ x[0],  16);
    x[1]  += x[6];    x[12] = rol32(x[12] ^ x[1],  16);
    x[2]  += x[7];    x[13] = rol32(x[13] ^ x[2],  16);
    x[3]  += x[4];    x[14] = rol32(x[14] ^ x[3],  16);

    x[10] += x[15];   x[5]  = rol32(x[5]  ^ x[10], 12);
    x[11] += x[12];   x[6]  = rol32(x[6]  ^ x[11], 12);
    x[8]  += x[13];   x[7]  = rol32(x[7]  ^ x[8],  12);
    x[9]  += x[14];   x[4]  = rol32(x[4]  ^ x[9],  12);

    x[0]  += x[5];    x[15] = rol32(x[15] ^ x[0],   8);
    x[1]  += x[6];    x[12] = rol32(x[12] ^ x[1],   8);
    x[2]  += x[7];    x[13] = rol32(x[13] ^ x[2],   8);
    x[3]  += x[4];    x[14] = rol32(x[14] ^ x[3],   8);

    x[10] += x[15];   x[5]  = rol32(x[5]  ^ x[10],  7);
    x[11] += x[12];   x[6]  = rol32(x[6]  ^ x[11],  7);
    x[8]  += x[13];   x[7]  = rol32(x[7]  ^ x[8],   7);
    x[9]  += x[14];   x[4]  = rol32(x[4]  ^ x[9],   7);
}

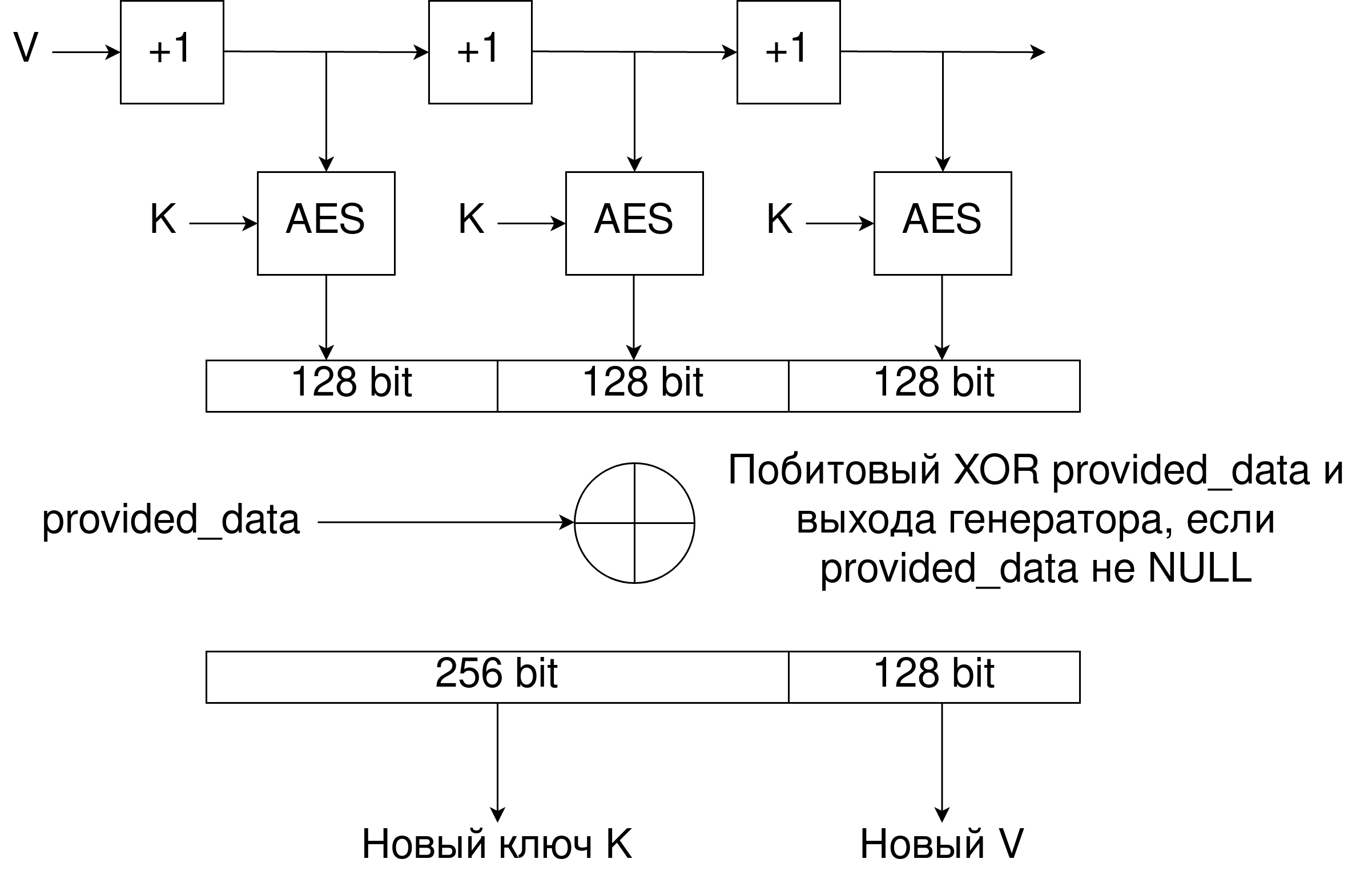
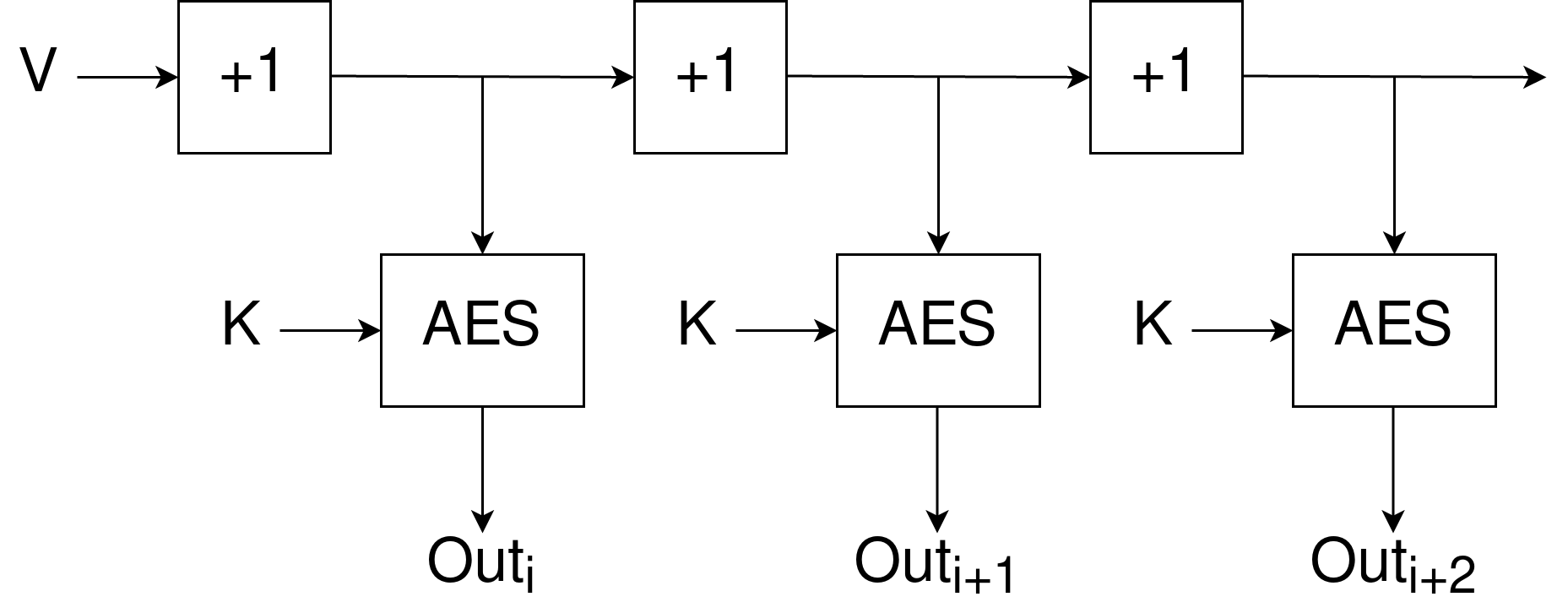
• SP800-90 AES CTR DRBG (англ.: CounTeR mode Deterministic Random Byte Generator) - это криптографически стойкий генератор псевдослучайных чисел, основанный на блочном шифровании AES (англ.: Advanced Encryption Standard) в режиме счетчика. Текущее состояние генератора описывается тремя объектами: ключ K, вектор V, который является счетчиком, и счетчик повторного заполнения counter. В упрощенном виде процесс создания выходной последовательности можно разбить на 2 части:

  • Создание ключа K и начального вектора V при помощи алгоритма обновления и дополнительных входных данных;

  • Создание необходимых псевдослучайных чисел, происходит шифрованием счетчика, при этом счетчик инкрементируется после каждого шага. Само шифрование происходит при помощи алгоритма AES с сгенерированным ключом. Таким образом этот алгоритм лишен необходимости дополнительного перемешивания начального состояния после каждого обращения, как это было в ChaCha.

Случайные события

Осталось разобраться с самым интересным - чем инициализировать ГПСЧ, чтобы получать действительно случайные числа? Кроме того, проблема состоит не только в инициализации, но и в постоянной переинициализации, которая необходима для предотвращения возможности предсказания следующего состояния. Вот тут и начинается самая интересная и важная работа по поиску случайности в событиях в системе.

Linux

Основные правила выбора событий, которые расцениваются как случайные. Во-первых, эти события должны быть недетерминированные. Во-вторых, их должно быть тяжело пронаблюдать извне. Эти случайные события добавляются в пул энтропии (просто массив чисел), перемешиваясь с его содержимым с помощью специальной CRC-подобной хэш-функции. Она выполняется быстро, чтобы ее можно было применять после каждого интересующего события в системе, и достаточно хороша, если предполагать, что случайные события заполняют пул не вредоносным образом. При этом при добавлении события в пул, происходит учет прибывшего количества энтропии.

В данный момент используется 4 типа источников случайных событий:

• Информация от устройств, которая должна быть разной на физически разных машинах, например MAC адрес сетевой карты. Фактически, это не добавляет энтропии системе, но позволяет в очень плохих случаях (запуск с одного образа) на разных устройствах получать разные состояния;

• Информация от таймера, прерывания, типа прерывания, значения;

• Время прерывания;

• Информация о времени поиска блока на диске. Однако на современных SSD это достаточно плохой источник случайности, так как у них время поиска сравнительно маленькое и примерно одинаковое всегда.

Чтобы инициализировать или переинициализировать ГПСЧ, необходимо из пула энтропии достать несколько случайных байт. Для этого, весь пул хэшируется алгоритмом SHA-1, а хэш-сумма выдается как случайный набор бит. При этом предпринимаются меры для обеспечения безопасности генератора в будущем. Во-первых, результат хэширования перемешивается с пулом, чтобы по выходному значению нельзя было восстановить текущее состояние. Во-вторых, происходит постоянная оценка оставшегося количества энтропии в пуле.

Из-за последнего существует 2 способа взаимодействия со случайными числами в Linux - /dev/random и /dev/urandom. Первый блокируется, когда оценка по количеству энтропии становится ниже нуля, а второй выдает числа всегда, даже если пул не пополняется случайными битами. При этом числа все еще могут оставаться достаточно случайными для требуемой задачи.

Стоит добавить, что на многих шагах, где это имеет смысл, в коде добавлены обращения к "железным" генераторам случайных чисел, которые работают быстрее и дают более качественную энтропию. Это, возможно, было бы не так важно, но Intel еще в Ivy Bridge добавили инструкции RDRAND и RDSEED, позже и AMD сделали это. Таким образом у многих современных компьютеров в CPU есть быстрый генератор случайных чисел. Почему это необходимо - будет объяснено в заключении.

Windows

В Windows процесс создания случайных чисел подчинен достаточно сложной древовидной структуре. Есть три типа источников энтропии, которые отличаются предназначением и качеством. Энтропия, получаемая из них, используется для инициализации и переинициализации корневого ГПСЧ - все случайные числа тем или иным образом получаются из него. Так как в современных многоядерных компьютерах было бы непозволительно медленно иметь только один генератор, то для каждого логического CPU, создается свой ГПСЧ, который инициализируется корневым. Далее, на каждый пользовательский процесс, заводятся и инициализируются свой ГПСЧ и его дочерние генераторы для каждого логического CPU. Таким образом мы получаем что-то вроде дерева генераторов.

Все генераторы, кроме корневого, переинициализируются, когда понимают, что их состояние устарело. Это происходит с помощью ведения и сравнения эпох. Счетчик инкрементируется каждый раз, когда корневой генератор переинициализируется. При этом каждый из его "потомков" в дереве локально запоминает состояние счетчика при его собственной переиницализации. Корневой генератор заполняется по расписанию - при загрузке системы, а далее с экспоненциально растущим периодом: 1, 3, 9, 27 секунд и т.д. Максимальное значение периода составляет 1 час.

В качестве источников энтропии в Windows используются:

• Время прерываний (основной источник) - при каждом прерывании берется отметка о времени с помощью чтения с TSC (англ.: TimeStamp Counter) и записывается в специальный массив на 256 байт компактным образом;

• TPM (англ.: Trusted Platform Module) - выдает 40 байт на старте и 64 байта при каждой переинициализации, но из-за ограничений, не может этого делать чаще, чем раз в 40 минут;

• RDRAND/RDSEED - "железные" генераторы, предоставляемые процессором;

• Seed файл - запись в реестре, которая создается ОС во время работы и используется во время следующей загрузки;

• Внешняя энтропия - запись в реестре, которая делается установщиком для первого запуска системы, но также может быть использована пользователем в будущем, чтобы влиять на процесс инициализации;

• ACPI-OEM0 - создается гипервизором Hyper-V и заполняет при каждом запуске гостевой ОС;

• Данные из драйверов - хэшируются и представляются как очень плохой источник энтропии, который, однако, позволяет по-разному инициализировать систему на разных физически машинах;

• UEFI - случайные числа из UEFI-драйвера;

• Отметка о времени старта системы - не очень хороший источник, но снижающий вероятность того, что, стартуя с одного образа системы, машины получат одинаковые состояния;

• Уникальное (не случайное) число от Hyper-V - помогает бороться с повторением состояния при запуске снапшота системы.

Во время старта системы данные с 7 источников (Seed файл, внешняя энтропия, TPM, RDRAND, ACPI-OEM0, UEFI и время старта) хэшируются SHA-512 и используются для инициализации SP800-90 AES-CTR-DRBG. Уже во время работы системы, данные предоставленные источником, помещаются в пул (за исключением первого раза, когда они идут сразу на переинициализацию корневого ГПСЧ).

Заключение

Как можно было заметить, многие источники случайных событий связаны с текущим состоянием машины, следовательно при виртуализации могут начаться проблемы. В Linux в комментариях к коду иногда открыто признается эта проблема. В Windows с Hyper-V (или другим гипервизором, "прикидывающимся" им) пытаются с этим бороться, но сама проблема все же иногда проявляется. Ситуация несколько облегчается, тем фактом, что в современных процессорах есть "железные" генераторы случайных чисел, а так же существуют виртуализированные генераторы, которые подсовывают случайные числа хостовой ОС гостевой. Ведь нельзя оставлять это на волю случая...

Литература

Linux
Windows
ChaCha20
SP800-90 AES-CTR-DRBG