06.12.2021 10:53
olegsmirnov_elbrus 9 5300 Источник

Привет, Хабр, я Олег, преподаватель Elbrus Bootcamp. Возможно, вы слышали о латинских квадратах. Раньше считали, что они защищают от зла и помогают в магических ритуалах, а теперь их используют в криптографии и играх.

В моем пет-проекте футошики латинский квадрат является игровым полем. Потребовалось генерировать такие квадраты быстро, не задерживая пользователя даже на 100 миллисекунд, но делать их непредсказуемыми и разнообразными. Оказалось, что генерация латинского квадрата — все еще проблема. Я погуглил и выяснил, что на русском языке информации о способах ее решения почти нет.

Решил исправить ситуацию: в этой статье расскажу об алгоритмах генерации и их ограничениях, и покажу, как реализовал один из алгоритмов на JavaScript. А еще объясню, почему магический и латинский квадрат — не одно и то же.

История латинского квадрата

Латинские квадраты — это такие квадратные таблицы, в которых символы не должны повторяться в каждой строке и в каждом столбце.

Первые находки, связанные с латинскими квадратами, датируют ещё 10-11 веком [1]. Тогда люди верили в то, что амулеты, содержащие латинские квадраты, защищают от зла и помогают в магических ритуалах для призыва демонов. Самая первая книга, содержащая латинские квадраты, опубликована примерно в 1200 году.

Может возникнуть ассоциация с другими квадратами, которые называются магическими. Но между этими двумя квадратами есть очень большая разница. Магические квадраты, в отличие от латинских, могут быть построены только для чисел и требуют, чтобы совпадала сумма всех элементов в каждой строке и столбце и на диагоналях, а сами числа не повторялись во всём квадрате. В латинских же квадратах набор чисел в каждой строке и столбце одинаковый, меняется только их порядок.

Одной из важнейших вех в развитии латинских квадратов стало исследование Эйлера. Именно он дал название латинским квадратам и первым описал их математически, а также применил для их исследования математические методы.

В современном мире латинские квадраты активно используются для протоколов шифрования, в планировании научных экспериментов, в коммуникационных протоколах для коррекции ошибок, в статистике и играх.

Первое практическое применение латинского квадрата было как раз для шифрования — полиалфавитный шифр Тритемия использовал простейший латинский квадрат. Но и в современной криптографии латинский квадрат используется часто. В 2005 году разработчики потокового шифра Edon80 использовали в своём алгоритме целый конвейер из 80-ти специально подобранных латинских квадратов. Кроме этого, латинский квадрат используется и в схемах разделения секрета.

Есть и совершенно неожиданные способы применения. Например, латинские квадраты использовались в агрономических исследованиях, для минимизации влияния разных экспериментов друг на друга.

И, конечно, нельзя не упомянуть использование латинских квадратов в других играх, кроме уже упомянутой футошики. Поле знаменитой игры «Судоку», конечно, является латинским квадратом, но добавляет к нему несколько новых правил, чтобы играть было интересно. Кстати, на занятиях в Elbrus Bootcamp студенты создают для нее автоматический решатель.

Алгоритмы генерации

Хотя правила латинского квадрата очень просты, а история их исследования насчитывает не одну сотню лет, всё ещё существует проблема генерации латинского квадрата. Разные задачи требуют разных характеристик алгоритма. Среди прочего важны:

  • Алгоритмическая сложность в зависимости от размера квадрата

  • Количество памяти, необходимое для генерации

  • Равномерность вероятности попадания каждой цифры в каждую ячейку квадрата

Квадрат характеризуется числом n— размером одной его стороны. Давайте рассмотрим некоторые из существующих алгоритмов генерации латинского квадрата [2].

Метод Косельни

Самым быстрым способом сгенерировать латинский квадрат является метод Косельни. Он создаёт новый квадрат на основе двух других, меньшего размера. Сложность этого алгоритма O(n^2) и это самый быстрый из известных алгоритмов. Большим минусом этого метода является то, что итоговый квадрат не будет равномерно распределённым, а потому не может быть использован в криптографии. Да и в игре его не особо используешь, готовые квадраты уж слишком похожи друг на друга.

Реализацию метода можно посмотреть здесь.

SeqGen с перегенерацией строки

Это единственный алгоритм, обладающий равномерной вероятностью попадания каждой цифры в каждую ячейку. К сожалению, это одновременно один из самых медленных методов. Вряд ли вы дождётесь окончания его работы для квадратов размером более 200, так как время его работы экспоненциально зависит от размера. Можем оценить его вычислительную сложность как O(e^n)

Реализацию метода можно посмотреть здесь.

SeqGen с графом замен

Этот алгоритм — нечто среднее между предыдущими двумя. С одной стороны, он достигает приемлемого равномерного распределения только на очень больших размерах квадратов, 256 и больше. С другой стороны, он способен сгенерировать квадраты такого размера за приемлемое время. Сложность этого алгоритма приближается к O(n^3)

Реализацию метода можно посмотреть здесь.

Метод Джейкобсона и Мэтьюза

Отличный выбор, если мы хотим как можно ближе приблизиться к равномерному распределению чисел при адекватной алгоритмической сложности. Этот алгоритм способен дать нам квадрат очень хорошего качества, но при этом работает строго за O(n^3), в отличие от предыдущего, который часто может закончить генерацию быстрее.

Реализацию метода можно посмотреть здесь.

Разбор алгоритма Джейкобсона и Мэтьюза

Хотя для моей задачи, для генерации совсем небольших квадратов, хватило бы и SeqGen с перегенерацией строки, я всё же выбрал именно алгоритм Джейкобсона и Мэтьюза. Он одновременно и достаточно быстрый, и даёт очень близкое к равномерному распределение. А еще он весьма интересен в реализации, что в итоге стало главным критерием. В отличие от всех предыдущих, этот алгоритм рассматривает латинский квадрат не как матрицу, а как трехмерный куб.

Куб инцидентности

Куб инцидентности — это альтернативное представление матрицы латинского квадарата. Он представляет собой куб размером n \times n \times n, где каждая ось соответствует строкам, колонкам и символам латинского квадрата.

Ячейка куба (a, b, c)содержит 1, если на пересечении строки a и колонки b находится символ c. В ином случае ячейка содержит 0.

\def\arraystretch{1.3} \begin{array}{|c|c|c|c|} \hline 0 & 1 & 2 & 3 \\ \hline 1 & 2 & 3 & 0 \\ \hline 2 & 3 & 0 & 1 \\ \hline 3 & 0 & 1 & 2 \\ \hline \end{array}

Для этого квадрата у нас будут следующие ненулевые ячейки:

\def\arraystretch{1.3} \begin{array}{|c|c|c|c|} \hline (0, 0, 0) & (1, 0, 1) & (2, 0, 2) & (3, 0, 3) \\ \hline (0, 1, 1) & (1, 1, 2) & (2, 1, 3) & (3, 1, 0) \\ \hline (0, 2, 2) & (1, 2, 3) & (2, 2, 0) & (3, 2, 1) \\ \hline (0, 3, 3) & (1, 3, 0) & (2, 3, 1) & (3, 3, 2) \\ \hline \end{array}

Соответствующий матрице куб инцидентности:

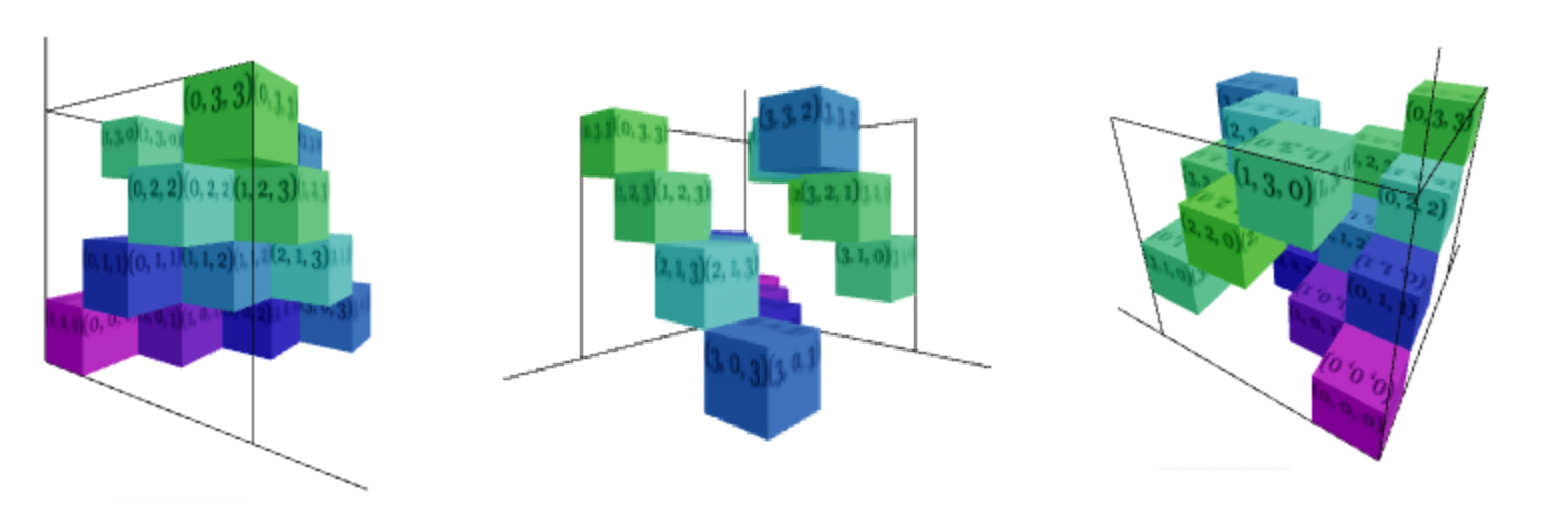
Куб инцидентности с разных сторон
Куб инцидентности с разных сторон

Описание шага

Шагом алгоритма мы будем называть добавление и вычитание единицы в некоторых ячейках куба таким образом, чтобы не изменять сумму элементов в каждой строке по всем трём осям куба. Эта сумма всегда должна быть равна 1. В процессе хода может образоваться ячейка, содержащая значение -1. Так как сумма строки обязана быть неизменной, в строке со значением -1 будет присутствовать две ячейки со значением 1.

Куб, содержащий ячейку со значением -1, мы будем называть незаконченным.

Будем различать два типа шагов: из законченного куба и из незаконченного куба.

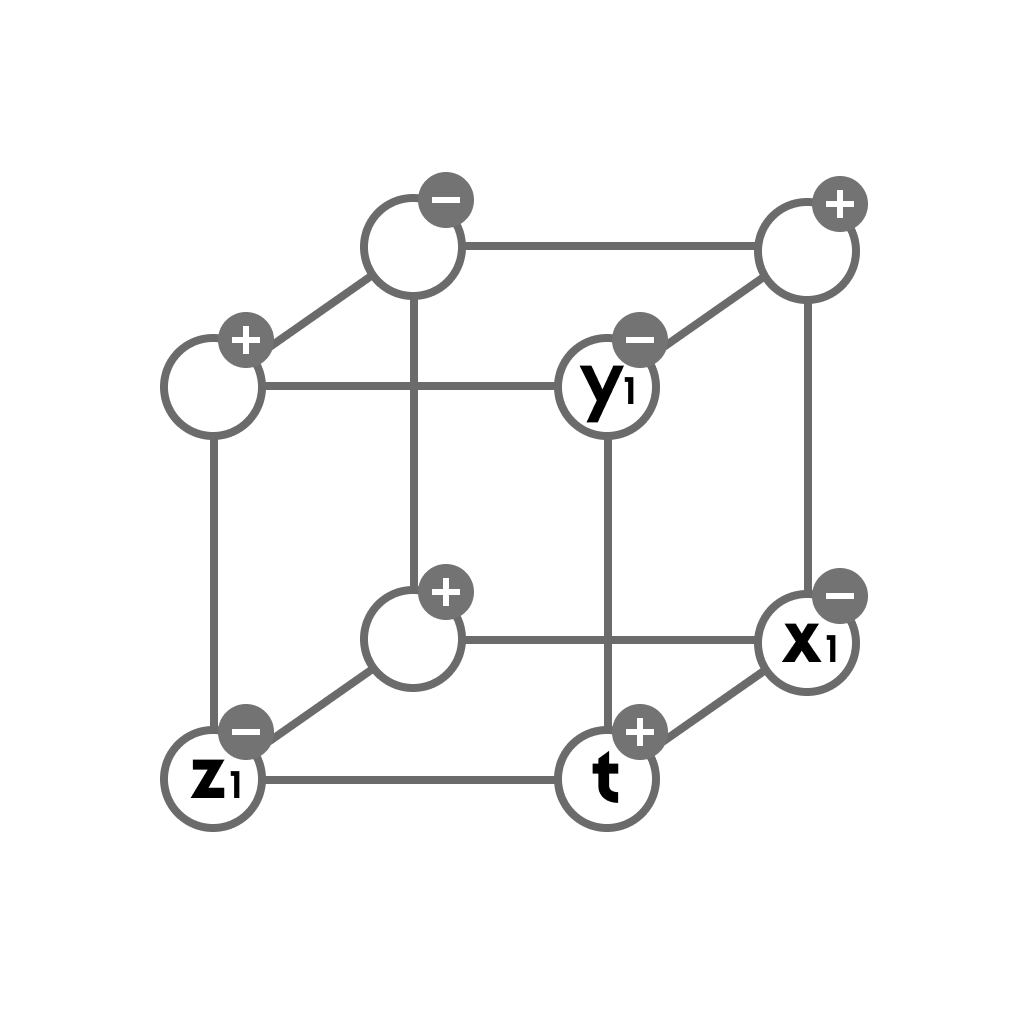
  1. Для шага из законченного куба мы выбираем из куба любую ячейку со значением 0. Назовём эту ячейкуt, её координаты будут (t.x, t.y, t.z)Эта ячейка связана с тремя строками в кубе, каждая из строк параллельна одной из осей и в каждой строке находится только одна ячейка со значением 1. Назовём координаты таких ячеек x_1, y_1и z_1соответственно. Таким образом мы получаем подкуб размером 2 \times 2 \times 2. Этот подкуб не обязательно будет состоять из соседних клеток. Шагом в таком случае будет добавление 1к(t.x, t.y, t.z)и вычитание 1таким образом, чтобы в каждой строке по каждой оси сумма всех ячеек осталась равна. Визуальное отображение шага показано выше. Если после совершения шага противоположная tячейка c координатами (x_1, y_1, z_1)содержит значение -1, то получившийся куб считается незаконченным. В ином случае куб законченный.

  2. Для шага из незаконченного куба алгоритм вычитания и добавления остаётся прежним, но меняется алгоритм вычисления tи координат x_1y_1и z_1. В качестве значения tмы берём ячейку со значением -1. Такая ячейка в кубе может быть только одна. В строке x, соответствующей координате t.xнаходится одна ячейка со значением -1 и две ячейки со значением 1. В качестве x_1выбираем любую из этих двух ячеек. Аналогично поступаем с y_1и z_1После этого хода мы точно так же можем получить как законченный, так и незаконченный куб.

Джейкобсон и Мэтьюз доказали [3], что любые два куба инцидентности связаны между собой конечным числом шагов. При этом таких шагов будет всегда не более 2(n-1)^3.

Получается, для генерации куба с максимально равномерным распределением необходимо соблюсти три ключевых условия:

  • для всех случайных значений нужно использовать качественный генератор случайных чисел;

  • необходимо повторить шаг алгоритма как минимум n^3раз;

  • только законченный куб можно преобразовать в корректный латинский квадрат.

Наивная реализация на JavaScript

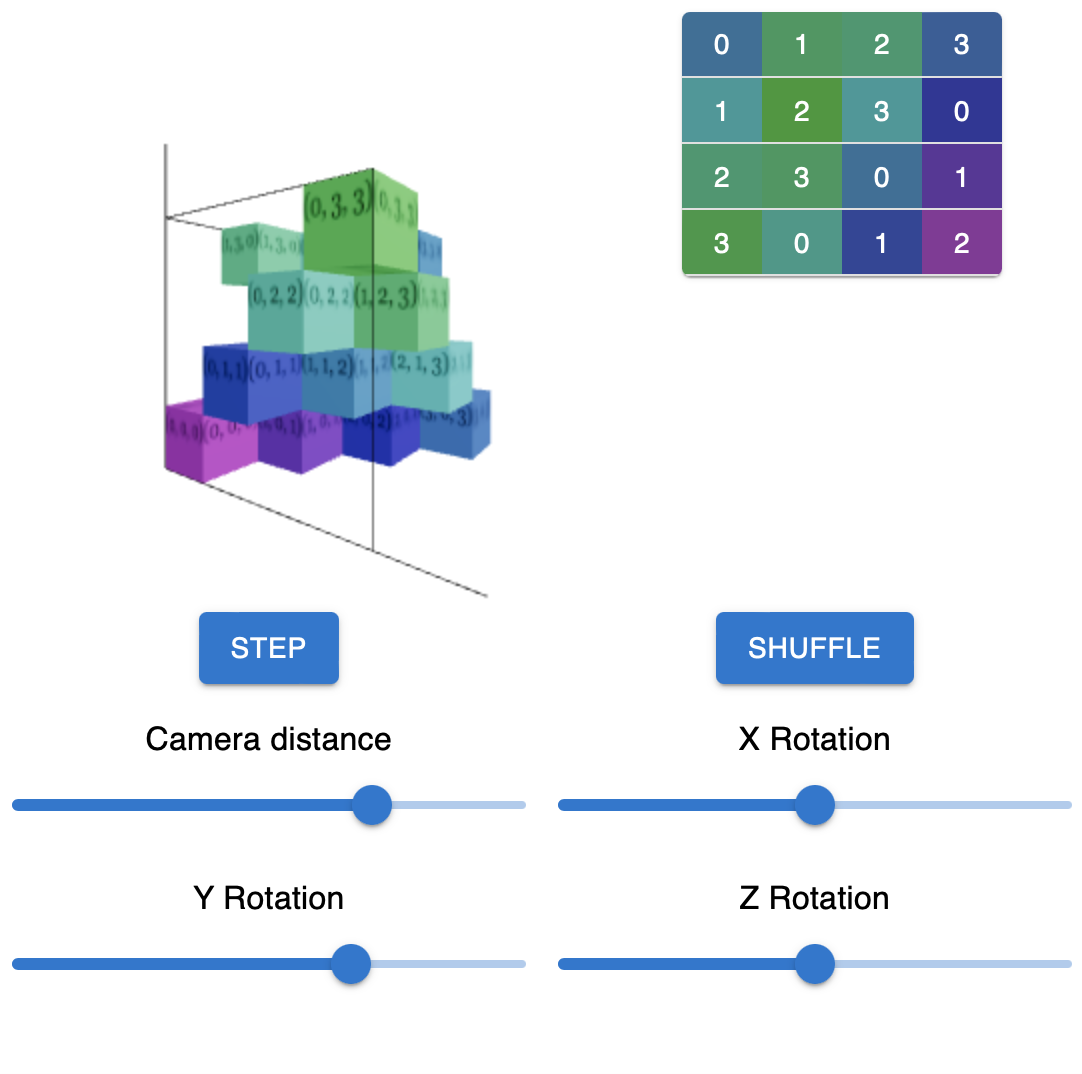
Я написал неэффективную, но легко читаемую реализацию алгоритма на JavaScript с визуализацией на React и Three.js, она доступна здесь. Вы можете вращать куб по всем осям с помощью соответствующих слайдеров, а также запускать алгоритм пошагово с помощью кнопки "Step" и запускать алгоритм целиком с помощью кнопки "Shuffle". Справа от куба отображается соответствующий ему латинский квадрат.

Реализация самого алгоритма находится в файле src/bl/IncidenceCube.js.

Что дальше?

Мы рассмотрели краткую историю латинских квадратов и варианты их применения, взглянули на уже известные подходы к генерации этих квадратов. Мы выяснили, что существующие алгоритмы очень сильно различаются по своим характеристикам, а потому должны подбираться в зависимости от конкретной задачи.

Мы взглянули на простейшую реализацию алгоритма Джейкобсона и Мэтьюза, которая, конечно, далеко не самая оптимальная. Сложность моего алгоритма — O(n^4)но его можно сократить как минимум до O(n^3)

Проблема текущей реализации состоит в том, что для каждого шага, зная x и y, мы можем очень долго искать местоположение ячейки, содержащей 1. В худшем случае это займёт O(n)Это можно значительно ускорить, например, сохраняя значения z-координат всех ячеек со значением 1 и, таким образом, сведя скорость поиска к O(1)Похожая оптимизация алгоритма Джейкобсона и Мэтьюза частично описана в работе Gallego Sagastume [4].

Код на JavaScript, представленный выше, генерирует квадрат 100 на 100 за 9 секунд. Слабо сделать на JS быстрее, чем за секунду?

Ссылки

  1. https://vbn.aau.dk/ws/portalfiles/portal/13649565/R-2007-32.pdf

  2. https://github.com/bluemontag/igs-lsgp

  3. https://onlinelibrary.wiley.com/doi/epdf/10.1002/(SICI)1520-6610(1996)4%3A6<405%3A%3AAID-JCD3>3.0.CO%3B2-J

  4. http://sedici.unlp.edu.ar/bitstream/handle/10915/42155/Documento_completo.pdf?sequence=1

Комментарии (9)


  1. mobi
    06.12.2021 11:18
    #23789889

    А не проще взять таблицу умножения для любой группы нужного порядка (проще всего, конечно, сгенерировать для циклической группы) и перетасовать столбцы/строки случайным образом?


    1. olegsmirnov_elbrus Автор
      06.12.2021 12:51
      #23790353
      +1

      На самом деле метод Джейкобсона и Мэтьюза в некоторой степени является вариацией того, что вы предложили :) Разница лишь в том, что в вашем предложении нет гарантий того, что вероятность попадания каждой цифры в каждую ячейку равномерна.

      Плюс, есть у меня такое ощущения, что таким образом у вас получится сгенерировать не каждый квадрат. Тут примерно как с кубиком Рубика, предложенные вами преобразования будут давать лишь подмножество множества всех корректных латинских квадратов. Хотя это надо отдельно доказывать, конечно.


      1. mobi
        06.12.2021 14:21
        #23790725

        Я имел в виду что-то такое (пример на питоне):


        import numpy

N = 10
idx1 = idx2 = numpy.arange(N)
numpy.random.shuffle(idx1)
numpy.random.shuffle(idx2)
A = numpy.fromfunction(lambda i, j: (idx1[i] + idx2[j]) % N, (N, N), dtype=int)


        1. olegsmirnov_elbrus Автор
          06.12.2021 17:15
          #23791401
          +1

          А, тогда это метод Косельни, только на основе двух массивов. Проблема та же самая что и у Косельни — итоговое распределение не равномерное. Особенно будет заметно на больших квадратах.

          Вообще нужно очень аккуратно складывать случайные значения. Хотя сами по себе они равномерно распределены, но по центральной предельной теореме у вас в итоге получится распределение, приближающееся к нормальному.

          В целом такой вариант мог бы использоваться для игр, я согласен :)


    1. samsergey
      08.12.2021 06:00
      #23797019

      Вот здесь есть подробная работа (диссертация) на тему перемешивания и генерации случайных латинских квадратов. Там показываются недостатки наивного метода (в первую очередь, проблемы с равномерностью распределения, во вторую -- с эффективностью) на больших квадратах. Метод Джекобсона-Мэтьюза один из оптимальных по своим характеристикам.

      А автору статьи спасибо за чудесную визуализацию метода!


      1. olegsmirnov_elbrus Автор
        08.12.2021 18:08
        #23799895
        +1

        Пытался найти эту информацию, но не смог. Спасибо за комментарий!


  1. mobi
    06.12.2021 18:44
    #23791793

    итоговое распределение не равномерное

    Почему?


    Вообще нужно очень аккуратно складывать случайные значения. Хотя сами по себе они равномерно распределены, но по центральной предельной теореме у вас в итоге получится распределение, приближающееся к нормальному.

    Если вас смутила запись (idx1[i] + idx2[j]) % N, то это просто компактная форма записи умножения для циклической группы. В этом месте можно было бы написать B[idx1[i], idx2[j]], где B — это таблица умножения некоторой группы соответствующего порядка. И, кстати, так как сложение происходит по модулю, то предельная теорема тут не применима.


    PS. Кстати, можно еще ввести третий случайный массив idx3 и перемешивать результат умножения lambda i, j: idx3[(idx1[i] + idx2[j]) % N]


    1. olegsmirnov_elbrus Автор
      06.12.2021 20:03
      #23792083
      +1

      Вы правы, моя ошибка.

      Убедили, я не вижу причин, почему бы распределение было бы неравномерным и ваш вариант теперь видится мне предпочтительным :)


  1. DaniilMisharev
    08.12.2021 15:57
    #23799275

    Статья супер! Спасибо!