Пролог:
Эта одна из статей серии "Производная как смысл жизни", сначала я хотел сделать одну огромную статью про почти все темы по дифференцированию, но я передумал и сделаю несколько статей, возможно так даже будет легче для людей которые пытаются найти конкретную для себя тему.
Начало
Для начала лучше ознакомиться со статьей о самой прозводной(скоро будет). Ну если вы ознакомились, или уже были ознакомлены то идем дальше.
Как мы уже знаем формула записи производной выглядит так:

-напоминаю, что Δx - приращение аргумента, Δy - приращение функции.
Мы должны понимать, что если мы уберем предел, то к f'(x) прибавиться коофициент, я ее называю "неточность".
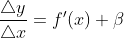
Так же вполне логично, что при Δx->0, β->0, так как чем меньше мы делаем разницу между x и x₀, тем меньше значение "неточности"(в статье о производной об этом подробнее рассказано).
Теперь выразим из этого равенства приращение функции(Δy):
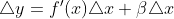
И на этом следует пока остановиться и рассмотреть график.
Смотрим дифференциалу в лицо
Расмотрим такой график:
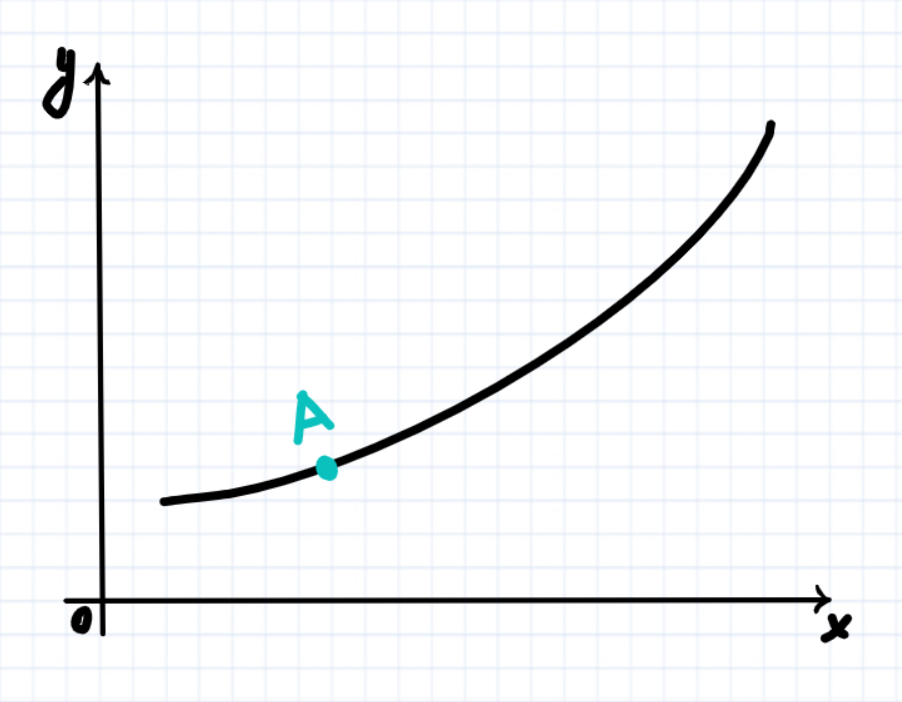
Как мы знаем производная в точке равняется значению тангенса угла в этой точке, то есть f'(x)=tg(α). Так что давайте обозначим производную, ну и приращения которыми она ограничена.

Как мы видим приращение функции(Δy) как бы разделено на две части: BC и CD.
И ведь по-сути нам ведь интересна именно та часть, которая показывает на сколько изменился у относительно касательной - то есть BC, а CD - это лишь та "погрешность" которая нам не особо интересна, поэтому введем понятие дифференциала:
Дифференциал(d) - это линейная часть приращения функции.
Дифференциал функции(dy) - это главная линейная часть приращения функции.
Зная это введем обозначение на графике:

Вернемся к равенству
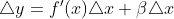
BD = Δy и мы знаем, что BD = BC + CD, а значит Δy = BC + CD, где BC мы назвали главной линейной частью приращения функции(dy), следовательно Δy = dy + βΔx.
Из формулы мы понимаем, что dy=f'(x)Δx.
Хорошо, мы определили чему равен дифференциал функции, а что же тогда является дифференциалом независимой пременной функции(аргумента).
Графически мы видим, что Δx никак не разделена касательной, то есть Δx это полное приращение функции, а значит dx = Δx.
Так же мы можем найти по формуле: dx = (x)'Δx = 1*Δx = Δx
И зная, что dy = f'(x)dx, мы можем выразить производную: f'(x)=dy/dx.
Немного пределов
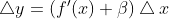
Добавим с левой части и с правой предел
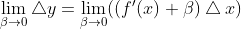
Тогда:

В самом начале мы сказали, что если β->0, то Δx->0 и наборот, а значит:

Зная, что f'(x)Δx = dy, мы делаем вывод, что:

Тогда так же мы можем сказать, что дифференциал функции - это приращения функции у которой приращение аргумента стремиться к нулю, ну и это следуется из того же графика.
В свою очередь dx по прежнему Δx
Комментарии (10)

belch84
08.12.2021 10:17Тогда так же мы можем сказать, что дифференциал функции — это приращения функции у которой приращение аргумента стремиться к нулю, ну и это следуется из того же графика.
Меня учили, что дифференциал — это главная линейная часть приращения функции при стремящемся к нулю аргументу
631052
08.12.2021 14:40+2это вообще очень интересная цитата.
дифференциал - это приращения функции
приращение стремиться
и из всего этого что-то там "следуется"

loginsin
08.12.2021 12:08+3Последняя формула вызывает большие сомнения. Если функция в точке x0 непрерывная и гладкая, то этот предел равен строго нулю.
PS: Не совсем понял, зачем писать свою вольную интерпретацию производной, которая достаточно строго и весьма внятно описана в школьных учебниках. Хабр молодеет?

itsoft
08.12.2021 12:39+5В заголовке кликбейт, в статье не увидел смысла жизни.
Статья начинается с формулы, а не с определения производной понятной крестьянину без всяких заумных значков. Именно так и портят мозги детям, что для них производная не скорость изменения функции, а вот эти закорючки.
Ничего не сказано про то, что производной может и не быть.
Ничего не сказано зачем нам производная.

631052
08.12.2021 14:43+2а еще там написано, что лучше начинать со статьи, которой тут еще нет.
кмк, немного странно

631052
08.12.2021 14:38может быть, есть смысл исправить опечатки? (и "ться" тоже)
еще вот написано, "я называю неточностью", в этой связи вопрос, кто еще ее так называет.

tarekd
09.12.2021 00:11Спасибо за статью. Как математику, сразу бросились в глаза несколько вещей
не определено в статье
затем появляется
Все же думаю что начинать нужно с формулы
а затем вводить объявления
. Иначе начинающие могут еще дальше запутаться.
Кстати, производная в этом случаем будет левая, и для гладких функций она будет совпадать с правой. Можно построить пример функции где они будут различны.

mayorovp
09.12.2021 00:57+1Э-э-э, а чего это производная левая будет?
У левой производной в формуле должно быть под знаком предела написано Δx→-0, у правой — Δx→+0. А у вас в комментарии написана формула обычной (двусторонней) производной.


Emelian
Чем-то напоминает книгу «Математические рукописи Карла Маркса», опубликованную советским академиком (точнее, членкорром) Рыбниковым. Правда, у дедушки Маркса эмоций было побольше, от модной, в то время, теории. Скажем, производной функции икс в квадрате он посвятил множество страниц, с какой только стороны ее не рассматривая, как же, даже в математике обнаружилось движение и диалектика! Хотя, для построения математической модели в «Капитале» ему хватило одной арифметики. Так что для школьников и студентов младших курсов, чтение матрукописей классика – самое оно!