На сегодняшний день случайность повсеместно используется в нашей жизни. Она есть в научных работах и исследовательских моделях, защитных алгоритмах и криптосистемах, в лотереях и азартных играх, системах автоматизации и математике. Сейчас я немного расскажу про ГСЧ и какие плюсы и минусы можно от них получить в той или иной сфере.

Как мы получаем последовательности случайных чисел?

Как уже было сказано выше, современный мир довольно сильно зависит от случайных чисел и нам необходимо как-то их получать. И сейчас мы имеем два способа генерации случайных последовательностей.

• Генератор истинно случайных чисел

Аппара́тный генера́тор случа́йных чи́сел (генератор истинно случайных чисел) — устройство, которое генерирует последовательность случайных чисел на основе измеряемых, хаотически изменяющихся параметров протекающего физического процесса.

Думаю, что данный вид генераторов является своего образа эталоном для получения случайных последовательностей, так как в своей работе они используют различные надежные источники энтропии. Но с другой стороны ГИСЧ имеют ряд недостатков: они громоздкие, дорогие в создании и настройке, а также медленнее программных алгоритмов.

• Генераторы псевдослучайных чисел

Генератор псевдослучайных чисел (ГПСЧ, англ. pseudorandom number generator, PRNG) — алгоритм, порождающий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному).

Наиболее распространенный тип генераторов в реальном мире. Они проще и дешевле, но имеют изъян в своей "псевдослучайности". Так что с развитием технологий человечеству приходится создавать новые ГПСЧ, которые защищены вычислительно сложной задачей от взлома машиной.

ГПСЧ

Конечно, как и любая технология, ГПСЧ должен обладать какими-то качествами. Согласно статье на Википедии, имеется 4 критерия:

• Достаточно длинный период, гарантирующий отсутствие зацикливания последовательности в пределах решаемой задачи. Длина периода должна быть математически доказана;

• Эффективность — быстрота работы алгоритма и малые затраты памяти;

• Воспроизводимость — возможность заново воспроизвести ранее сгенерированную последовательность чисел любое количество раз;

• Портируемость — одинаковое функционирование на различном оборудовании и операционных системах;

• Быстрота получения  элемента последовательности чисел, при задании элемента, для любой величины; это позволяет разделять последовательность на несколько потоков (последовательностей чисел).

Одним из первых ГПСЧ был линейный конгруэнтный генератор. Суть его заключалась в задании следующего числа последовательности с помощью предыдущего: . В данной формуле a, b, N и являются параметрами системы. Но у этого метода есть недостатки в виде небольшого периода, равного N, и зацикливаемости последовательности.

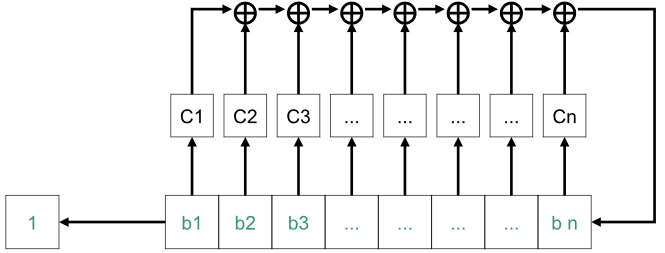
Также хочется сказать про РСЛОС (Регистр сдвига с линейной обратной связью). Данный генератор создает следующий бит производя операции умножения и сложения по модулю два над несколькими предыдущими значениями. Данный многочлен выдает период псевдослучайной последовательности не больший, чем

Описание РСЛОС

Рекуррентную формулу можно представить в виде:

где m - степень многолчена, а - коэффициенты многочлена.

"Вихрь Мерсенна" является одним из наиболее распространенных на данный момент ГПСЧ, а точнее его версия М19937, и реализован в стандартных библиотеках множества языков программирования. Этот алгоритм имеет большой период, равный и в нем тяжело выявить статистические закономерности.

Описание Вихря Мерсенна

Алгоритм генерирует двоичные слова размерностью w. Начальными значениями являются n векторов размерности w. Элемент n + p задается формулой:

где

• p, q, r - целые константы, p - степень рекуррентности, ;

• - w-битовое двоичное число;

• - двоичное число, полученное конкатенацией чисел и где первые w-r бит взяты из первого числа, а последние r бит из второго числа;

• - матрица размером определенная посредством

  Далее следует процедура "закалки", которая усиливает равномерность распределения векторов большой размерности.

Подробнее можно почитать [1] стр. 55-58.

Но данный генератор не используется в криптографии, так как не удовлетворяет условиям криптостойкого ГПСЧ (КСГПСЧ):

• КСГПСЧ должен удовлетворять "тесту на следующий бит": не должно существовать полиномиального алгоритма, который, зная первые k битов случайной последовательности, сможет предсказать k+1 бит с вероятностью, не равной ½;

• КСГПСЧ должен оставаться надежным, даже если известна часть внутренних состояний генератора. Если в алгоритме применяется дополнительный источник энтропии, то использовать значения данного источника для взлома генератора должно быть вычислительно невозможно.

Если говорить о примерах, то такие алгоритмы как ISAAC, алгоритм Yarrow или алгоритм Blum-Blum-Shub являются криптостойкими.

Использование ГПСЧ в нашей жизни

Разобравшись с понятием ГПСЧ, можно рассмотреть его область применения.

В основном, генераторы случайных чисел используются различных алгоритмах шифрования. К примеру, возьмем алгоритм RSA. Для его работы необходимо получать два больших случайных простых числа: p и q. И если эти два числа будут заданы не случайно, то не исключено возникновение проблем, связанных со взломом алгоритма.

Ещё случайные числа нашли свое место в науке при изучении различных явлений и моделей. Современная наука использует различные методы статистического анализа, в которых необходимо использование случайных чисел. В ещё большей степени ГСЧ необходимы при создании моделей реальных явлений. В случаях, когда требуется воспроизвести случайную последовательность, ГПСЧ имеет преимущество в виде начального значения, которое можно задать повторно и воспроизвести случайные числа.

В теории игр, где необходимо исследовать случайные комбинации предметов (шахматы, карты), и в теории вероятностей, которая изучает случайные величины.

Нельзя не сказать про азартные игры. ГСЧ нашли свое применение в лотереях и игровых автоматах, где необходима генерация случайных исходов. Также в компьютерных играх: раздача колоды карт, бросание костей или поведение неигровых персонажей. Везде, где можно использовать волю случая - используют машинную генерацию случайных чисел. А если знать внутреннее состояние ГПСЧ, то можно сорвать большой куш, предсказывая выходящие значения.

Заключение

Как мы видим, случайные числа прочно вошли в нашу жизнь и используются повсеместно. Но неслучайная случайность может наделать много проблем. Поэтому проверьте ваш ГПСЧ на соответствие всем стандартам вашей области прежде чем его использовать.

Список литературы

1. Слеповичев И.И. Генераторы псевдослучайных чисел

2. Википедия: ГПСЧ, ГИСЧ, ЛКГ, Вихрь Мерсенна, КСГПСЧ

3. Стандарты: NIST, ANSI, Росстандарт