Привет, Хаброжители! У нас вовсю продолжается распродажа «Старый Новый год».

Кто пытается арифметическими методами генерировать случайные числа, тот, конечно, живет во грехе. Поскольку, как указывалось уже неоднократно, нет такого феномена, как случайное число  —  есть только методы для получения случайных чисел.

– Джон фон Нейман

Генераторы случайных чисел (ГСЧ) – важнейшая составляющая разнообразных процессов, связанных с компьютерными программами, таких как криптография, моделирование, машинное обучение, игры, программирование, азартные игры, научные исследования – список можно продолжать. Но может возникнуть вопрос: как именно получить по-настоящему случайное значение, и почему это важно?

Оказывается, спонтанность — не самая сильная сторона компьютеров. Они
могут выполнять только те действия, на которые запрограммированы. Благодаря
ГСЧ, компьютеры приобретают способность генерировать уникальные неравномерно
распределенные числа. Иными словами, ГСЧ помогает компьютеру моделировать
непредсказуемость.

Два типа генераторов случайных чисел

Генераторы случайных чисел бывают двух разных типов: генераторы истинно случайных чисел (ГИСЧ) и генераторы псевдослучайных чисел (ГПСЧ) [1]. ГИСЧ считаются «истинными», так как используют в качестве источника энтропии внешний источник, расположенный за пределами компьютерной программы – например, погоду, атмосферные помехи или промежутки времени, в течение которых вы удерживаете клавиши на клавиатуре вашего компьютера.

Более строгие научные методы связаны с измерением радиоактивного распада атома [2]. Согласно квантовой теории, невозможно узнать наверняка, когда произойдет акт деления ядра, так что это, в сущности, «чистая случайность». Генерация истинно случайных чисел – это по-настоящему захватывающая тема, и мы посвятили ей целую статью, которая находится здесь.

ГИСЧ отлично подходят для создания подлинно случайных чисел, но работа таких генераторов зачастую отличается высокой вычислительной сложностью и не масштабируется, поскольку они зависят от внешних источников данных и от сенсоров.

Генераторы псевдослучайных чисел

Кажется, что ГПСЧ генерируют случайные числа, но на самом деле это только кажется [3]. Они сравнительно широко используются благодаря своей скорости и воспроизводимости результатов, поэтому они очень хорошо подходят для применения при моделировании и в играх. В сущности, ГПСЧ – это алгоритмы, использующие математические формулы или просто предвычисленные таблицы для выдачи последовательностей чисел [4]. Возьмем, к примеру, линейный конгруэнтный генератор (ЛКГ). В его составе используется начальное значение, множитель, инкремент и модуль.

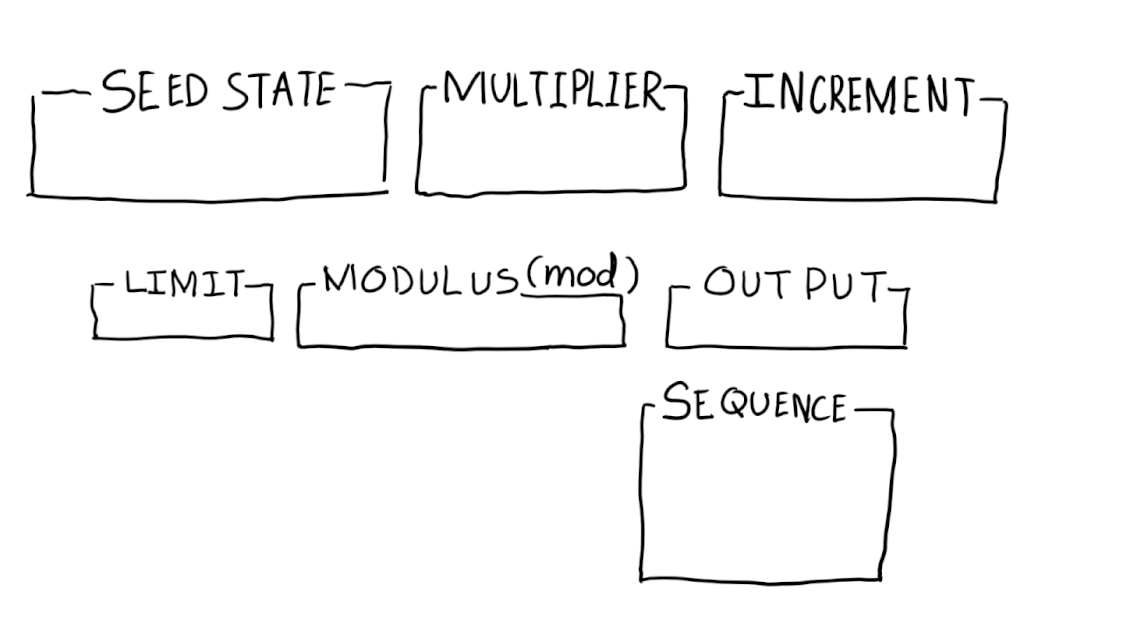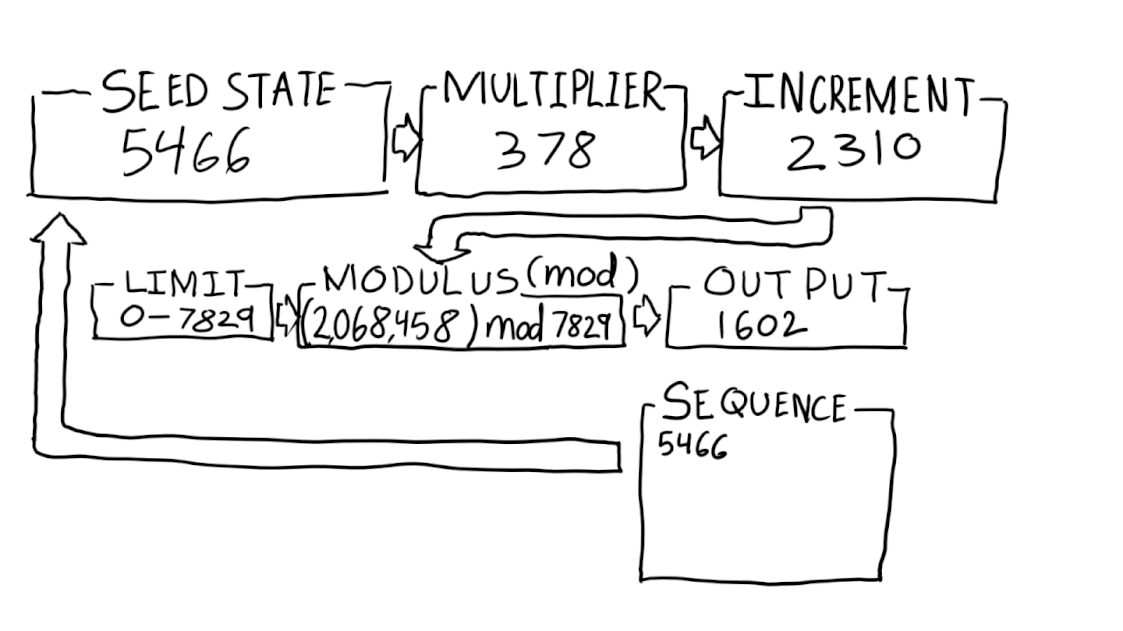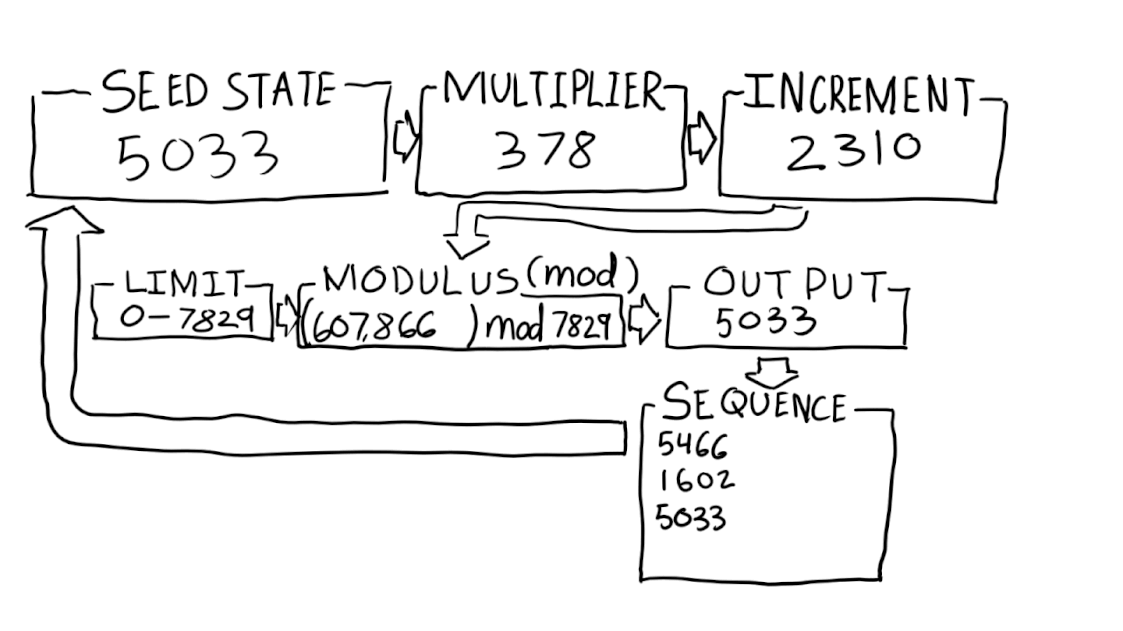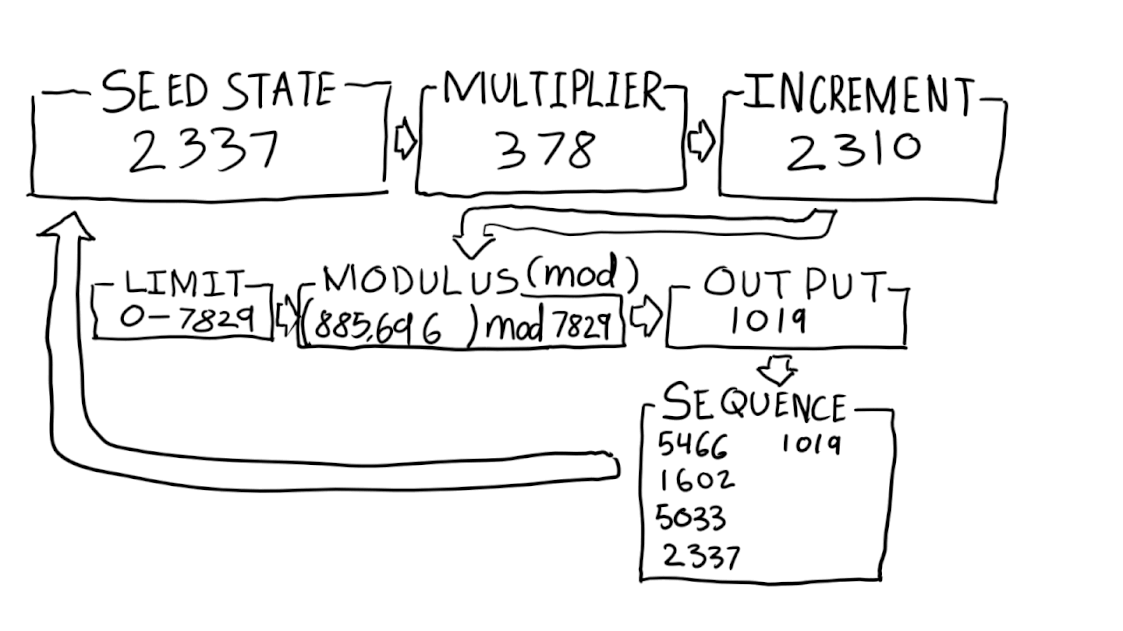
Рано или поздно, после некоторого количества попыток, последовательности начнут повторяться. Эта величина называется «период» и является мерой количества уникальных чисел в последовательности. ЛКГ не используются при шифровании, поскольку не обеспечивают достаточно надежной случайности. У них короткие периоды, а их паттерны равномерны.

В основе большинства ГПСЧ для шифрования лежит Вихрь Мерсенна. Этот генератор псевдослучайных чисел был разработан в 1997 году Макото Мацумото и Такудзи Нисимура и в настоящее время является наиболее распространенным неспециализированным ГПСЧ [5]. Назван он так потому, что имеет период 2¹⁹⁹³⁷− 1, такова длина простого числа Мерсенна. Вихрь Мерсенна по умолчанию используется во многих программных системах, в частности, в Microsoft Excel, MATLAB, Free Pascal, PHP, Python, R, Ruby и C++. Также он обычен в играх. К нему прибегают во многих системах, так как он позволяет быстро генерировать высококачественные псевдослучайные числа.

Способы использования игр

По мере того, как компьютерные игры становятся все реалистичнее, растет потребность и в более качественных генераторах случайных чисел. Сейчас ГПСЧ используются для создания геймплея, графики и обеспечения многих аспектов разработки игр. Когда ваш персонаж бьет противника, в игре требуется случайное число, чтобы аппроксимировать разброс нанесенного ущерба. В игре с ультрареалистичной графикой ГСЧ делегируется имитация отражений света, чтобы не перенапрягать процессор. В Minecraft случайное начальное значение используется для процедурной генерации мира вокруг вашего персонажа.

Игры такого типа, основанные на так называемой «процедурной генерации», в последние годы приобрели большую популярность. Причина проста: в них не приходится все делать вручную. Процедурный генератор – это система, использующая ГСЧ для создания целого мира по чисто случайному принципу [6]. В случае с “No Man’s Sky” в игре генерируется целая Вселенная. Процедурная генерация позволяет очень сильно экономить память, в то же время создавая почти неограниченное количество игровых локаций и персонажей. Без ГСЧ сделать это было бы просто невозможно, поскольку слишком сильно затрачивались бы ресурсы, и на большинстве устройств игра бы подвисала.

Конечно, здесь есть и недостатки. Для генерации каждой планеты в “No Man’s Sky” используется 64-разрядное начальное значение. Это число скармливается генератору биомов для создания ландшафта и других разнообразных атрибутов планеты. Но 64-разрядного числа в данном случае недостаточно, поэтому планеты не отличаются существенным разнообразием.

Порождающая последовательность запускается в игре всякий раз, когда вы входите в новую звездную систему [7]. Сначала вы видите большие разнообразные планеты с голубыми океанами и пышными зелеными лесами. Как только вы приступаете к исследованию планет, начинают вырисовываться различные варианты окружающей среды. Избыточные ландшафты и животные равномерно распределяются по поверхности планеты, и закономерности становятся очевидными.

С технической точки зрения, эти планеты получаются методом генерации случайных чисел, но ни одна из них не оставляет по-настоящему уникального впечатления. Игра может справляться только с небольшой вариативностью окружающей среды, отчасти из-за ограничений того ГПСЧ, который в ней используется. Чтобы справиться с такой дилеммой, нужен генератор случайных чисел с более длинным случайным значением. Если увеличить длину начального значения, получим больше переменных, но одного лишь этого будет мало. Один из атрибутов случайности заключается и в дисперсии чисел. Вы не хотите, чтобы одно и то же число попалось вам двенадцать раз подряд. Случайность получается и из того, насколько неравномерно распределены последовательности чисел. Вот почему фактор случайности так важен в играх.

Равномерность распределения псевдослучайных чисел можно проверить при помощи симуляции по методу Монте-Карло [8]. Методы Монте-Карло – это тип алгоритмов, которые раз за разом делают случайную выборку для получения численного результата. Их основная идея – в решении задач методом подбора случайных значений.

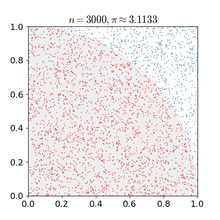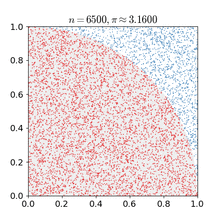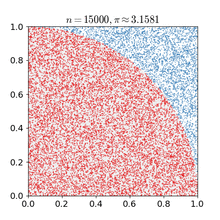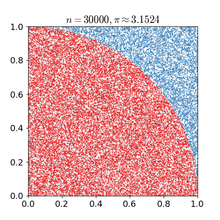
Обычно они используются для оценки неизвестных соотношений и областей. На рисунке выше метод Монте-Карло применяется для оценки значения числа Пи. Чтобы методы Монте-Карло были эффективны, в них не обязательно требуются истинно случайные числа. Часто при помощи детерминированных псевдослучайных последовательностей оказывается просто тестировать и повторно прогонять симуляции [9]. Рассмотрим, например, как робот-пылесос Roomba ориентируется по плану комнат в доме.

Роботы-уборщики наподобие Roomba используют для навигации безмодельный фреймворк машинного обучения [10]. Таким образом, они учатся методом проб и ошибок: вы формулируете роботу, какую цель нужно достичь, но не предоставляете ему конкретного плана действий.

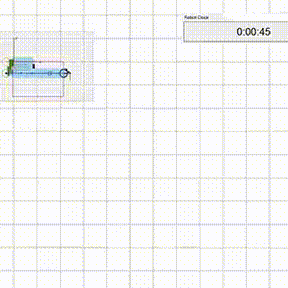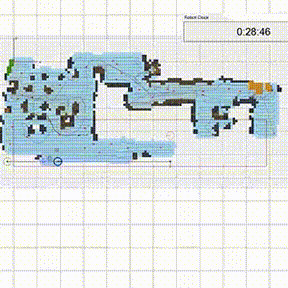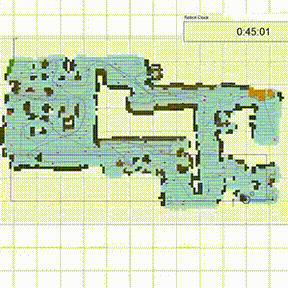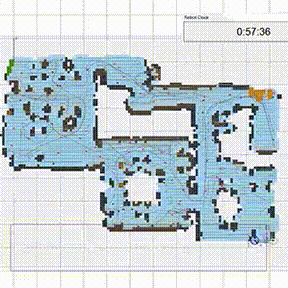
Tакой безмодельный фреймворк использует симуляцию по методу Монте-Карло, чтобы смоделировать планировку дома. Вместо того, чтобы просто покрывать всю возможную площадь дюйм за дюймом, он случайным образом выбирает точки, которые нужно найти, и так уточняет планировку. Входящие данные от сенсоров он использует, чтобы проверить, обошел ли уже весь пол. Закончив поиски, он возвращается в точку, которая соответствует началу координат.

Рандомизация домена (DR) – еще один способ использования случайности в машинном обучении. DR – это фреймворк машинного обучения, основанный на моделях. В нем применяется фиксированный набор правил, по которым учится ИИ [11]. Он используется в открытом проекте из области ИИ, связанном с моделированием ловкости рук.

Dactyl – это робот, обученный на множестве случайно подобранных симуляций, при помощи которых компьютер освоил естественные движения рук. Проект показал, что опыт обучения, заложенный в модель, составляет 100 лет. Машинное обучение такого рода было бы недостижимо, если бы учебные множества данных для него не генерировались при помощи ГСЧ.

Варианты использования в криптографии

Вы когда-нибудь задумывались, каковы механизмы шифрования в ваших полях с паролями и в браузере? Вы догадались: в основе цифрового шифрования лежат случайные числа [12]. Всякий раз, когда ваш браузер пытается обратиться за онлайновой информацией, она шифруется по методу SSL, что означает «слой защищенных сокетов».

Процесс начинается так:

• Сначала ваш браузер запрашивает идентификатор сервера.

• Затем веб-сервер направляет вашему браузеру в ответ на этот запрос SSL-сертификат.

• Браузер/сервер проверяют, можно ли доверять SSL-сертификату. Если можно, то на веб-сервер отправляется соответствующее сообщение.

• Веб-сервер отправляет обратно подтверждение, снабженное цифровой подписью и позволяющее начать сеанс, зашифрованный по технологии SSL.

• Зашифрованные данные совместно используются браузером/сервером с одной стороны и веб-сервером с другой стороны.

В принципе, именно так и происходит шифрование всех ваших данных, передаваемых онлайн.

История тайн

Использование фактора случайности для шифрования сообщений восходит ко временам древнего Рима. Римляне использовали шифр Цезаря, чтобы зашифровывать военные сообщения случайным ключом. В перемешивании для такого шифра использовалось всего 26 букв, поэтому вероятность взломать его составляла 1/26. Враг мог путем перебора попробовать все буквы латинского алфавита, и в таком случае на взлом кода ушло бы несколько часов, но к тому времени зашифрованные приказы уже были бы неактуальны.

По стандартам современной криптографии используется так называемая система одноразовых блокнотов. При использовании этого метода каждый символ в сообщении заменяется случайной буквой. Такой подход значительно снижает вероятность, что сообщение будет расшифровано. Допустим, вы хотите зашифровать имя “Alice”:

При рандомизации каждого символа в сообщении сложность его расшифровки возрастает экспоненциально. В случае с “Alice”, как в вышеприведенном примере, вероятность расшифровать это слово с первой попытки составляет около одного к 12 миллионам (26*26*26*26*26). Чем длиннее ключ, тем сильнее шифр.

Если вас интересует по-настоящему сложное шифрование, обратите внимание на SHA-256 [13]. SHA означает “Secure Hash Algorithm” (алгоритм криптографического хеширования). Он обычен в блокчейнах. Хеш-функция – это тип математической функции, преобразующей данные в отпечаток, именуемый «хеш-значением». Хеш-алгоритм – это функция, принимающая входные данные и преобразующая их в вывод фиксированной длины. Хеш-функция однонаправленная. Невозможно обратить данные из ее хеша; можно пройти путь от входных данных до хеша, но не наоборот.

У SHA-256 2^256 возможных исходов. Это число невероятно велико. Если бы все компьютеры на планете были задействованы для расшифровки всех возможных сигнатур этого сообщения, то на эту работу потребовался бы срок, в 37 раз превышающий возраст Вселенной. SHA-256 – основа защиты большинства блокчейнов, а также стандартный метод шифрования в АНБ и ЦРУ. Это одна из причин, по которым с технологиями блокчейна связаны такие большие ожидания.

Заключение

Истинная случайность непредсказуема, и ее сложно сгенерировать в компьютерных системах. В мире математики, где повсюду используются записанные данные и формулы для прогнозов, все сложнее найти что-то случайное. Но в этом и ценность. Люди, привыкшие искать паттерны, всегда будут ценить то, что не поддается предсказанию, особенно при защите приватности, которой сегодня уделяется такое внимание. Говорим ли мы о расчете при моделировании, о шифровании сообщений или о повышении фактора случайности в работе игровых автоматов, генераторы случайных чисел оказываются незаменимы в нашем обществе.

Источники

[1] Haahr, M. Introduction to Randomness and Random Numbers.

[2] John Walker, (1996). HotBits: Genuine random numbers, generated by radioactive decay.

[3] Christophe Dutang.,Diethelm Wuertz. (2009). A note on random number generation.

[4] Dave Ackley (2013). NMCS4ALL: Random number generators.

[5] Makoto Mastsumoto and Takuji Nishimura (1998).Mersenne Twister: A 623-dimensionally equidistributed uniform pseudorandom number generator.

[6] gregkwaste (2016). No Man’s Sky – Procedural Content.

[7] gkhan.(2015). A Short History of Randomness in Games (or “Why No Man’s Sky is just a pretty Pitfall!”).

[8] Dirk P. Kroese. (2011).Monte Carlo Methods.

[9] Will Knight. (2015).The Roomba Now Sees and Maps a Home.

[10] Vitchyr Pong. (2018). TDM: From Model-Free to Model-Based Deep Reinforcement Learning.

[11] Open AI.(2018). Learning Dexterity.

[12] Entrust(2005). Understanding Digital Certificates and Secure Sockets Layer (SSL).

[13] 3Blue1Brown. (2017).How secure is 256 bit security?