Введение
Математический анализ знает множество прекрасных функций с необычными свойствами. Среди них интегральные синус и логарифм
, также нельзя не отметить гамма-функцию
или очень известную дзета-функцию Римана
. Но сегодня я предлагаю читателю посмотреть на функцию W-Ламберта
Что такое W-функция Ламберта?
Для того, чтобы понять, что такое W-функция Ламберта, достаточно посмотреть на следующее равенство, которое по аналогии с основным тригометрическим тождеством предлагаю именовать "основное Ламбертово тождество":
Другими словами, функция Ламберта - обратная для . Однако после первых же исследований станет понятно, что
не инъективна, а именно одно и то же значение
достигается при двух разных аргументах, если
. Поэтому данное выше определение требует пояснений.
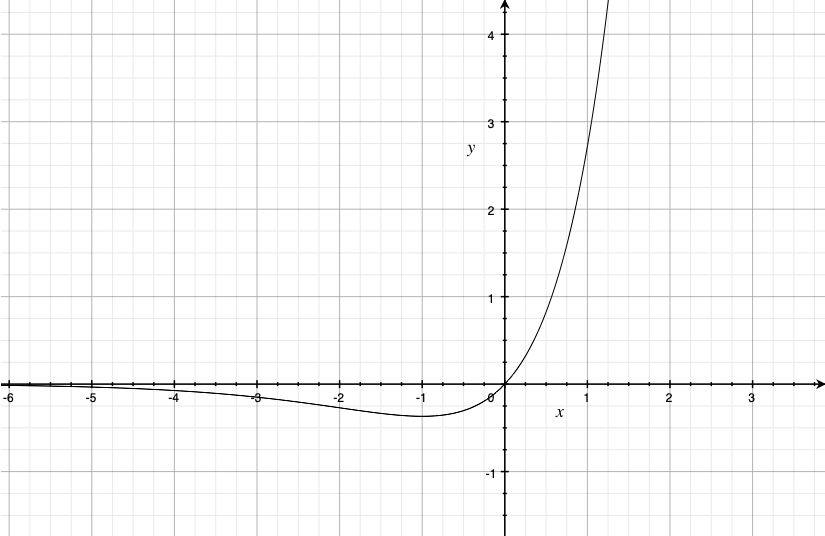
Исследовав производную функции , понимаем, что функция возрастает на
и убывает на
. Таким образом, давайте построим обратную функцию к данной на соответствующих промежутках монотонности.
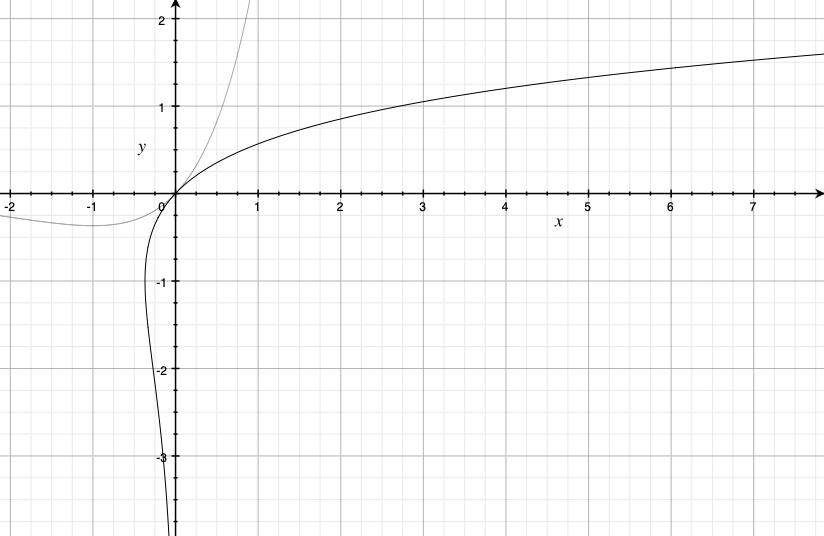
Ветвь, для которой , называется
, другая -
.
Постановка задачи
Задача. Научиться находить действительные корни уравнения следующего вида:
Как вы, наверное, уже догадались, для решения будем использовать W-функцию Ламберта. Итак, сначала возведем и левую, и правую часть в степень (это преобразование не является равносильным при четных целых
, а при нечетных нужно будет расширять множество значений
до всех действительных чисел, поэтому решаем задачу для указанных выше ограничений).
Теперь для того, чтобы воспользоваться основным Ламбертовым тождеством, нам нужно получить выражение с такое, как и в показателе степени экспоненты. Для этого поделим и левую, и правую часть на
.
И теперь мы можем воспользоваться основным Ламбертовым тождеством:
Откуда и получаем уже итоговую формулу для .
Вычисление W-функции Ламберта
Заметим, что при функция Ламберта дает два действительных значения: по одному на каждой из ветвей
и
соответственно. В этом случае у изначального уравнения будет 2 корня.
Вычисление W0. Будем использовать метод бинарного поиска по ответу. Мы можем так поступить, поскольку возрастает на
.
Левая граница бинарного поиска понятна и равна. Теперь возникает вопрос, как выбрать правую границу. Первая идея, которая приходит на ум: положить ее равной
, ибо верно неравенство
, причем равенство достигается только в нуле.
Однако для достаточно больших это может быть не лучшим вариантом. Поэтому давайте посмотрим на другой: выберем правую границу равной
.
Итого: при правой границей выбираем
, а при
берем
.
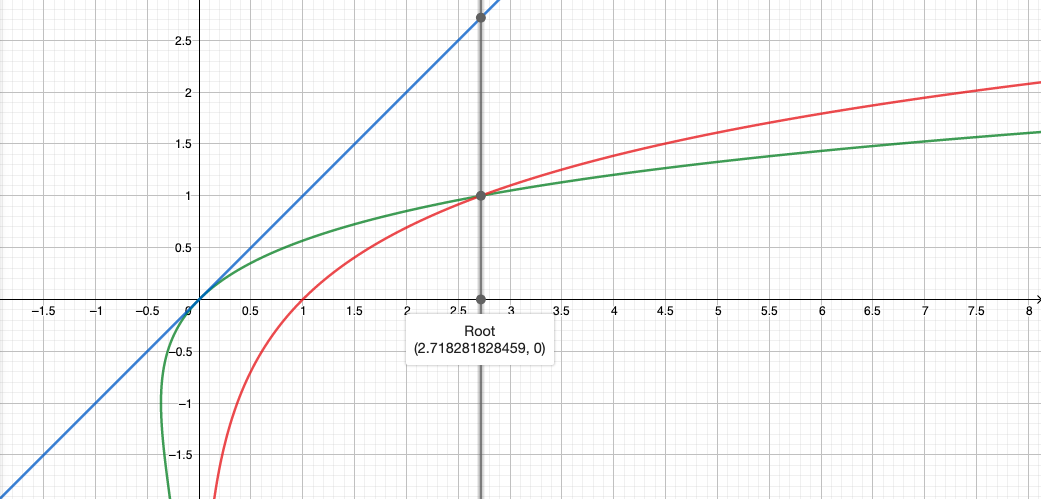
Ассимптотика: , prec - изначально выбранная точность (например, 10-12)
Вычисление W-1. Здесь будем использовать следующее бесконечное выражение для :
Чем глубже мы спускаемся, тем выше точность вычислений.
Реализация на Python
from math import *
def LambertW0(x):
left = -1
right = x if x <= e else log(x)
prec = 10**-12 # точность
# бинарный поиск
while right - left > prec:
mid = (right + left) / 2
if mid * exp(mid) > x:
right = mid
else:
left = mid
return right
def LambertW_1(x, t): # t - показатель точности
if t == 100:
return log(-x)
else:
return log((-x)/(-LambertW_1(x, t + 1)))
def sol(p, q):
s = q**(1/p) / p
if s < -exp(-1):
return "No real solutions"
ans = "Solutions: " + str(p * LambertW0(s)) + " "
if -exp(-1) < s and s < 0:
ans += str(p * LambertW_1(s, 0))
return ans
p = float(input())
q = float(input())
print(sol(p, q))Проверка
Уравнение 1.
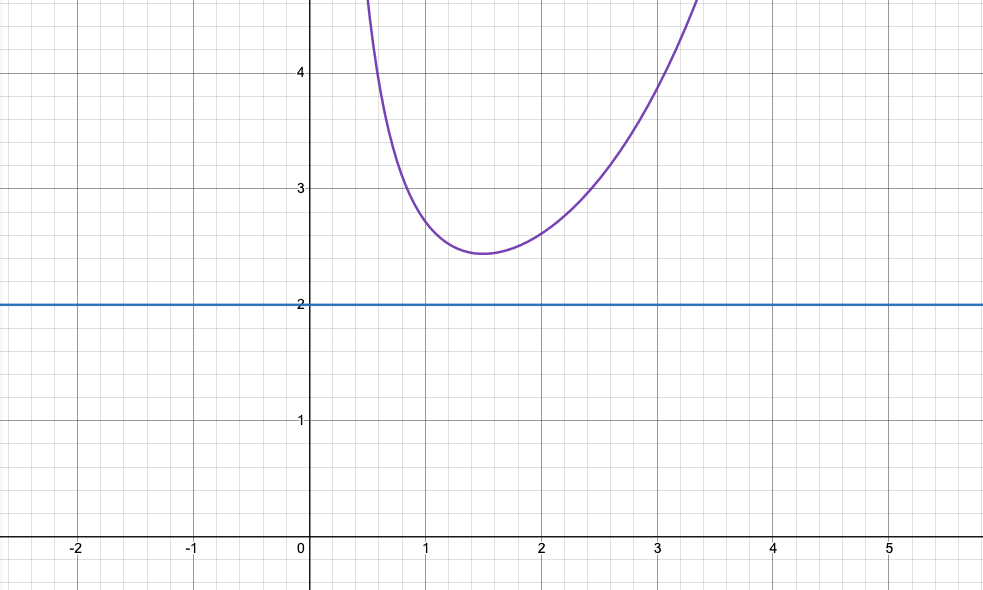
Уравнение 2.

Уравнение 3.


Заключение / выводы
Значения на 0 и -1 ветви W-функции Ламберта могут быть достаточно точно вычислены за короткое время, что делает возможным решение некоторых типов уравнений.
Комментарии (11)

belch84
14.05.2022 10:41+2Можно подойти к решению уравнения

немного иначе.
Функция Ламберта является решением обыкновенного дифференциального уравнения (ОДУ)
Если доступно средство для численного решения дифференциальных уравнений, можно найти его решение, и вычислить корень по приведенной в публикации формуле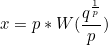
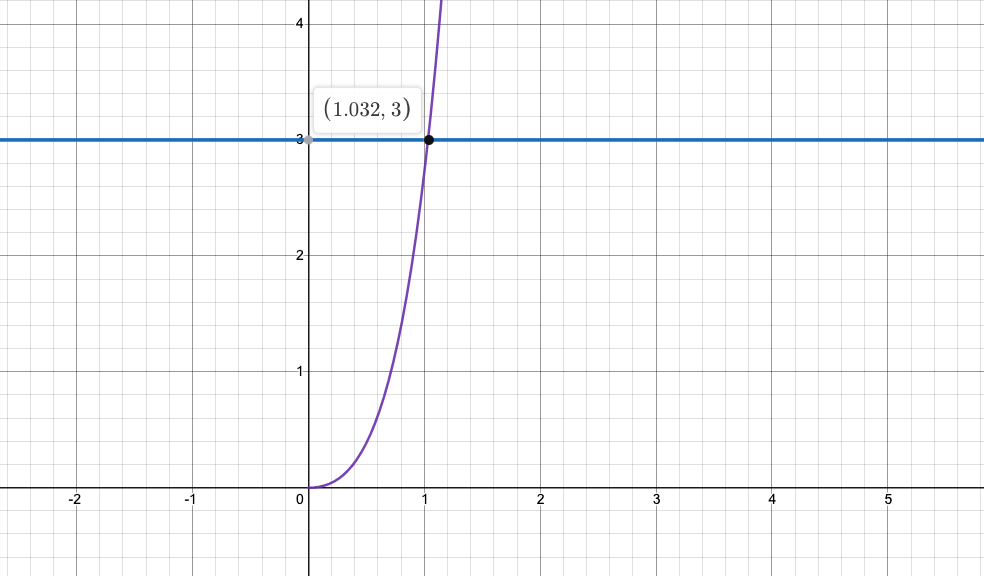
Конечно, численное решение дифференциального уравнения устроено намного сложнее, и при этом трудно достигнуть очень высокой точности, но при наличии готовой программы для решения ОДУ можно решить исходное уравнение совсем без программирования. Для уравнения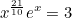
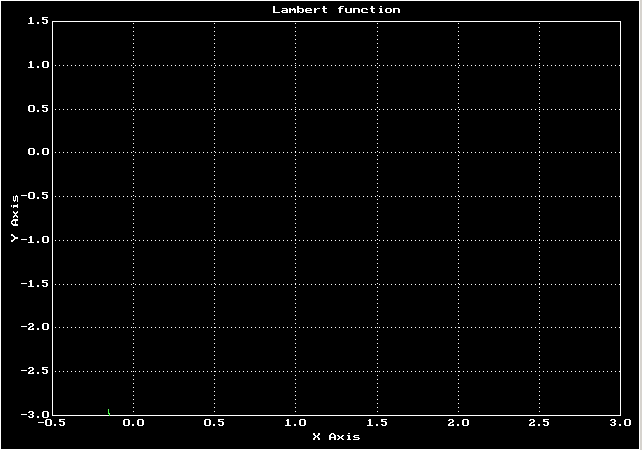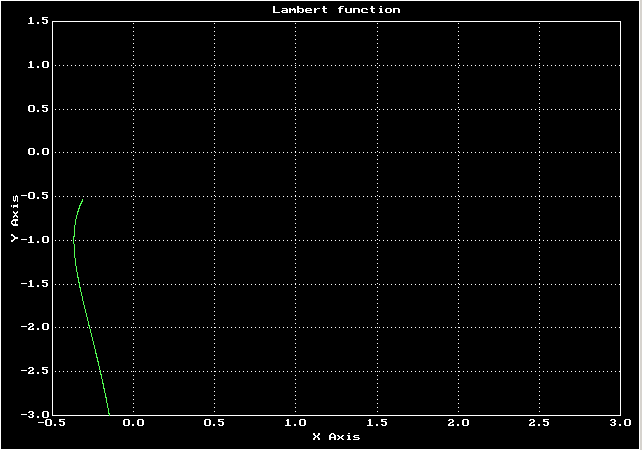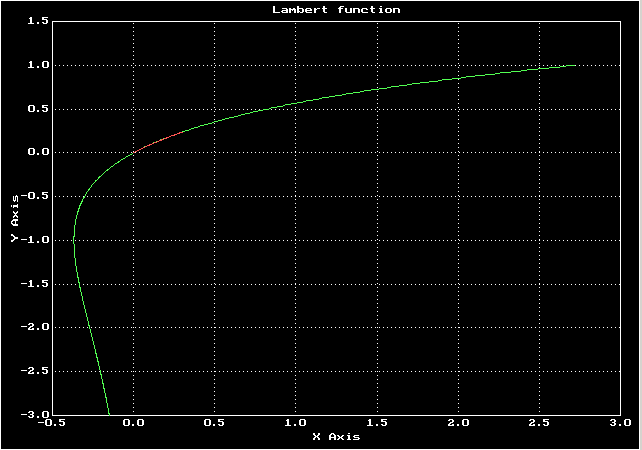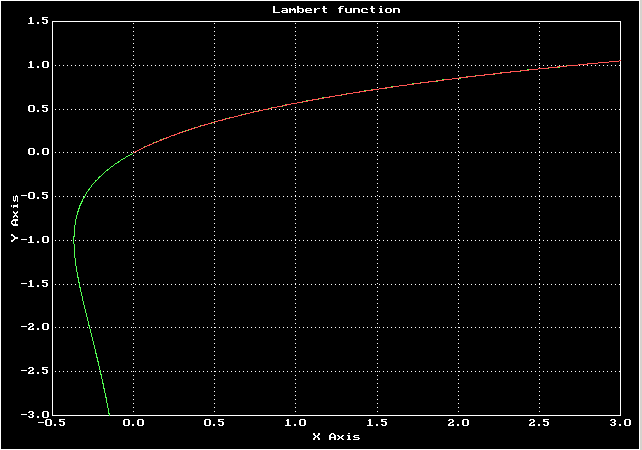
у меня получился корень 1.03215Сравнение точного графика ф-ции Ламберта и решения дифференциального уравнения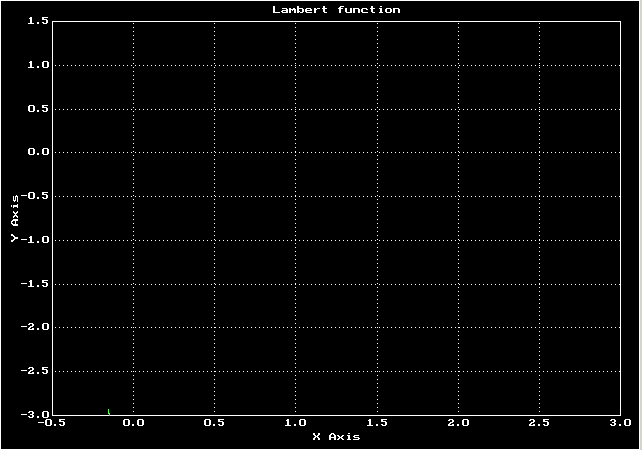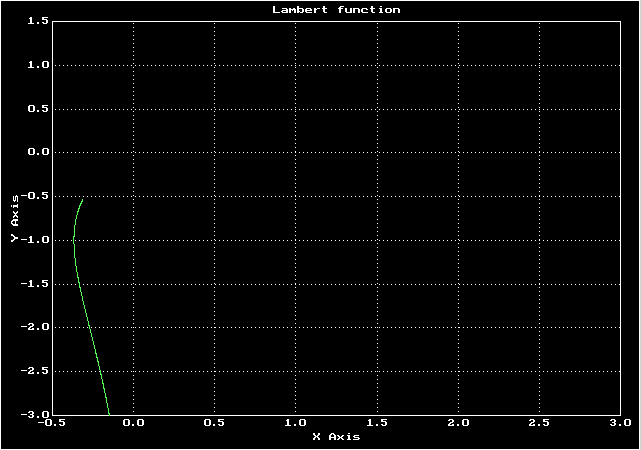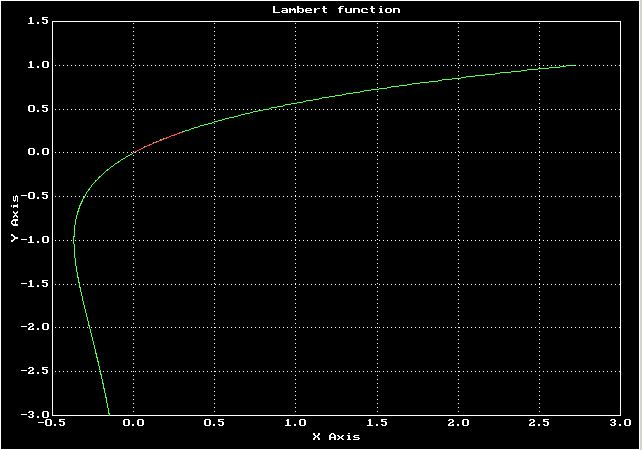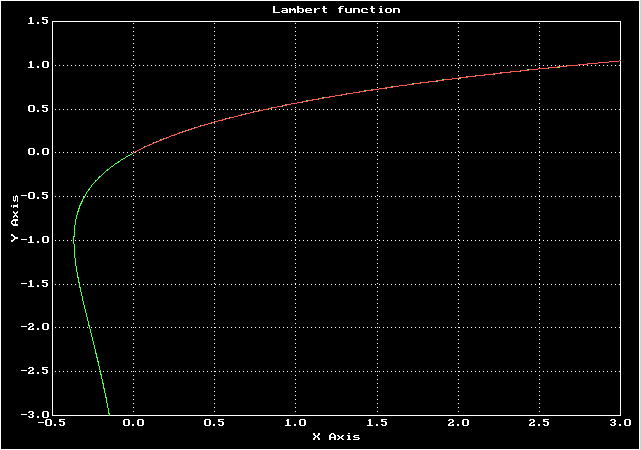
Зеленый — график функции Ламберта, красный — решение дифференциального уравнения






KvanTTT
В детстве в школе "изобрел" тетрацию или гипероператор-4 (только потом узнал как это называется). И только когда вырос, узнал, что некоторые уравнения с тетрацией решаются с использованием W-функции ламберта. Самое простое:
Так что эта функция вызывает у меня приятные ностальгические воспоминания :)
Разве не более эффективней раскладывать в ряд Тейлора и не использовать ни логарифмы, ни рекурсию? https://en.wikipedia.org/wiki/Lambert_W_function#Asymptotic_expansions
Sdima1357
x^x=x для х не равного 0 имеем х^(х-1) = 1 , имеет два вполне очевидных корня +1 и -1 или я что-то путаю?
KvanTTT
Извините, опечатался. Имел в виду
x ^ x = k, гдеk— константа. В решении написано правильно сk.e1vanov Автор
Доброй ночи! Я использую рекурсию и логарифмы при подсчете значений так называемой -1-ветви функции Ламберта, а разложение в ряд Тейлора дает значение 0-ветви в окрестности нуля
KvanTTT
Кстати, можно переписать функцию так, чтобы не использовать рекурсию, так эффективней, как-то так:
e1vanov Автор
Да, хороший вариант
KvanTTT
Если использовать тетрацию, то запись уравнения выглядела бы так:
x^^2 = k.alxndrlsn
любопытно... а меня с некоторых пор "тревожила" идея "мультипликата", в основе которой лежит предположение о том, что если для интегрируемой функции g(x) имеется ее первообразная G(x), то для функции f(x) представленной в виде экспоненты в степени g(x), тоже должна быть некая первообразная F(x) (и может даже только одна?), получаемая из f(x) некоторым преобразованием ("мультиплицированием"), которое соответствует интегрированию степени экспоненты (прошу прощения за невнятное пояснение, лучше взгляните на рисунок - осторожно! может быть заразно!):
Может быть, кто-то тоже переболел такими "фантазиями" и разрешился от них?