28.05.2022 01:42
xcont 14 4200 Источник
Продолжим тему бильярдных фракталов.



В статье присутствуют Gif (трафик!) и контрастные картинки. У эпилептиков может случиться эпилептический припадок.


Предыдущие части: 0, 1, 2.

Для начала вспомним, что за «бильярдные фракталы».

Бильярдные фракталы.



Есть у нас некоторая прямоугольная область («бильярд»), в которой движется бильярдный шар (или луч света).



Шар упруго отражается от стенок по законам оптики (угол отражения равен углу падения). При этом шар бесконечно мал (абстрактная «материальная точка» из физики) и при движении и отражении скорости не меняет (скорость нас вообще не интересует).

Когда шар касается одной из выбранных стенок (не важно, какую стенку выбирать, но для примера выберем верхнюю) — фиксируем, в какую сторону движется шар — в левую или в правую:





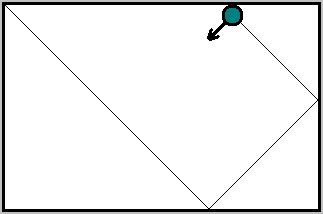
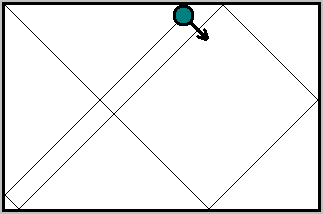
Для бильряда, соотношение сторон которого — иррациональное число, последовательность отражений — фрактальная (насколько этот термин применим к двоичным последовательностям). Или фракталообразующая. Если визуализировать такую последовательность с помощью черепашьей графики, мы получим фрактал.

В качестве примера можем использовать последовательность для бильярда, соотношение сторон которого равно $\sqrt {2}$.

Строить такие последовательность очень легко:

$Q_x=\lfloor x\sqrt {2} \rfloor \; (\textrm{mod} \; 2); \quad x=0,1,2,…$



Берем поочередно каждое целое число $x$, умножаем на $\sqrt {2}$, отбрасываем дробную часть и отмечаем четные целые части единицами, а нечетные — нулями.

JavaScript 
let a=[];
for(let x=0;x<100;x++) a[x]=Math.floor(x*Math.sqrt(2))%2;
console.log(a.join(''));



Первые 100 элементов этой последовательности:

0100110110010011001001101100110110010011011001101100100110010011011001001100100110110011011001001100

Визуализация этой последовательности с помощью черепашьей графики дает нам следующую фигуру:



Более подробно о том, откуда взялась эта формула и о визуализации последовательностей с помощью черепашьей графики, можно почитать во второй части — Фракталы в иррациональных числах

В реальном мире.



В реальном мире, такие последовательности встречаются гораздо чаще, чем может показаться на первый взгляд. Два примера.

Пример 1. Есть у нас два человека. Один побольше, второй — поменьше:



Эти два человека идут по улице. У высокого шире шаг, чем у низкого. Чтобы успевать за высоким, низкому приходится быстрее ногами двигать и больше шагов делать. В каждый момент времени, когда низкий ставит правую ногу на асфальт, фиксируем какая нога высокого находится в воздухе — левая или правая. Если частоты шагов низкого и высокого несинхронизированные — получим фрактальную последовательность.

Пример 2. Вокруг некоторой планеты вращается спутник:



Выбираем временной интервал $t$ произвольной длинны. Фиксируем в каком полушарии находится спутник в момент времени $t, 2t, 3t, ...$ — в южном или северном. Последовательность этих положений будет фрактальной, если соотношение длинны выбранного интервала с длинной интервала, за который спутник совершает полный оборот вокруг оси — иррациональное число.

Для наглядности, посмотрим на геометрическую интерпретацию бильярдных последовательностей.

Дискретизация линейной функции.





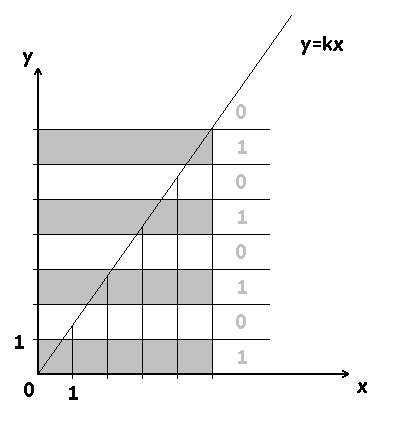
Для бильярда, соотношение сторон которого равно $k$, строим график функции $y=kx$. Целые числа, отмеченные на оси $y$, делят плоскость на чередующиеся полосы (поочередно помечаем полосы единицами и нулями). Целыми числами на оси $x$ отмечаем, через какую полосу проходит график функции — через полосу помеченную единицей или нулем.

Фактически, все что мы сделали, чтобы получить фрактальную последовательность — дискретизировали линейную функцию с иррациональным коэффициентом $k$. Если фрактальную последовательность можно получить дискретизацией линейной функции, первым делом напрашивается вопрос — а какую последовательность можно получить дискретизацией нелинейной функции?

Но прежде, чем переходить к нелинейным функциям, хотелось бы упомянуть об одном интересном наблюдении, сделанном в процессе написания статьи.

Об одном интересном наблюдении.



Дабы не нарушать структуру статьи...
Черепашья графика — не единственный способ визуализации двоичных последовательностей. Существует еще один способ, которому посвящена отдельная статья Фракталы в иррациональных числах. Часть 2. Вспомним этот способ.

Возьмем нашу последовательность:

$Q_x=\lfloor x\sqrt {2} \rfloor \; (\textrm{mod} \; 2); \quad x=0,1,2,…$



И построим из нее другую последовательность:

$a_x=\begin{cases}a_{x-1}+1, & \text{for } Q_x=1;\\a_{x-1}-1, & \text{for } Q_x=0;\end{cases}\; \quad x=0,1,2,…$



Первый элемент последовательности — произвольное число. Каждый следующий элемент — увеличиваем предыдущий элемент на 1, если соответствующий элемент первой последовательности ($Q$) равен 1, или уменьшаем на 1 — если соответствующий элемент равен 0.

JavaScript 
	let a=[50];
	for(let x=1;x<size;x++){
		if(Math.floor(x*Math.sqrt(2))%2==1)
			a[x]=a[x-1]+1;
		else
			a[x]=a[x-1]-1;
	}



После чего можем построить фрактальную кривую, отметив на графике точки с координатами $(x, a_x)$:

JavaScript 
	for(let x=0;x<size;x++){
		context.fillRect(x, a[x], 1, 1);
	}





Из этой же кривой можем получить фрактальную поверхность. Для каждой точки $(x, y)$ считаем $z=a_x+a_y$.

Дальше можем сделать срез плоскости по оси $z$:



Или отметить такие точки, для которых $z(\textrm{mod} \; 4)=0;$ или $z(\textrm{mod} \; 4)=1;$



Следующая картинка — чем больше $z$, тем ярче пиксель:



Можем немного изменить последовательность:

$a_x=\begin{cases}a_{x-1}+\{x\sqrt {2}\}, & \text{for } Q_x=1;\\a_{x-1}-(1-\{x\sqrt {2} \}), & \text{for } Q_x=0;\end{cases}\; \quad x=0,1,2,…$



Раскрыв скобки, получим:

$a_x=\begin{cases}a_{x-1}+\{x\sqrt {2}\}, & \text{for } Q_x=1;\\a_{x-1}+\{x\sqrt {2} \}-1, & \text{for } Q_x=0;\end{cases}\; \quad x=0,1,2,…$



Здесь $\{x\sqrt {2}\}$ — дробная часть, которую мы ранее отбрасывали.

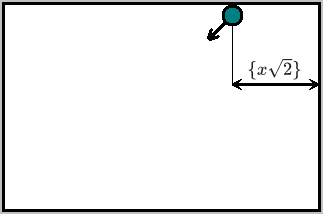
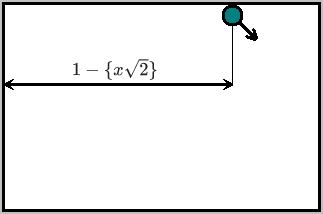
Как это выглядит в бильярдной модели? Мы увеличиваем предыдущий элемент последовательности на расстояние (по оси $x$) между правой границей и точкой касания шара верхней границы, если шар двигался влево. Или же уменьшаем на расстояние между левой границей и точкой касания шара верхней границы, если шар двигался вправо:





JavaScript 
	let c, arr=[0];
	for(let i=1;i<size;i++){
		c=i*Math.sqrt(2);
		if(Math.floor(c)%2){
			arr[i]=arr[i-1]+(c-Math.floor(c));
		}else{
			arr[i]=arr[i-1]-(1-(c-Math.floor(c)));
		}
	}

После раскрытия скобок:
	let c, arr=[0];
	for(let i=1;i<size;i++){
		c=i*Math.sqrt(2);
		arr[i]=arr[i-1]+(c-Math.floor(c));
		if(Math.floor(c)%2!=1){
			arr[i]--;
		}
	}


На самом деле...
Достаточно:
	let c, arr=[0];
	for(let i=1;i<size;i++){
		c=i*Math.sqrt(2);
		arr[i]=arr[i-1]+(c-Math.floor(c));
	}

В этом случае поверхность получится гладкой, а не фрактальной.



Делаем визуализацию тем же способом, который использовали выше. Для каждой точки $(x, y)$ считаем $z=a_x+a_y$. Получили поверхность. Раскрашиваем. Чем больше $z$, тем ярче пиксель:



До того, как мы изменили последовательность, все $z$ были целыми числами. Теперь — иррациональные. Сделать $z(\textrm{mod} \; 4)$ не получится. Но можем найти некоторую плоскость, которая находится на одинаковом расстоянии от максимальной и миниальной $z$ и посмотреть на точки, которые лежат ниже и выше этой плоскости:



Самое интересное получится, если мы отметим пиксели, для которых $\lfloor zk \rfloor \; (\textrm{mod} \; 2) =1;$. Другими словами, отмасштабируем $z$, умножив на некоторое число $k$, после чего отбросим дробную часть и проверим четность целой части. Для некоторых $k$:

478:


338:


Получаем замечательные круги. Примечательно, что круги получаем для $k$ равных числителю или знаменателю дроби, дающей приближенное значение $\sqrt{2}$

$\frac{478}{338}\approx\sqrt{2}$

Для других $k$:

144:


354:


Замечательные круги не получаем.

Здесь можно посмотреть в динамике, поводив мышкой по экрану.


Вернемся к дискретизации нелинейных функций.

Дискретизация нелинейной функции.



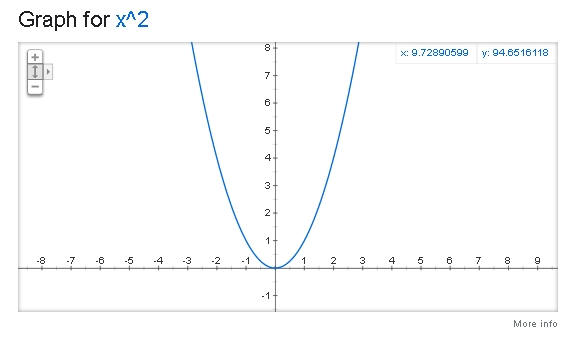
Например $y=kx^b$, где $b$ — действительное число. Самый простой пример — парабола ($y=kx^2$).



Строим последовательность:

$Q_x=\lfloor x^{2}\sqrt {2} \rfloor \; (\textrm{mod} \; 2); \quad x=0,1,2,…$



JavaScript 
let a=[];
for(let x=0;x<100;x++) a[x]=Math.floor(x*x*Math.sqrt(2))%2;
console.log(a.join(''));



Для целых аргументов $x$, записываем четность целой части (отбросив дробную) значения функции.

Первые 100 элементов этой последовательности:

0110010100111110000011000100010100000001010011010110001100101001010011111000000000100110111111111000

Визуализация этой последовательности с помощью черепашьей графики дает такую кривую:



Эта последовательность выглядит немного более хаотичной, чем последовательность, полученная дискретизацией линейной функции. Но это не так. Если где-то не видим закономерность — значит плохо смотрим. Можем сделать очень простую визуализацию. Запишем первые 1000 элементов последовательности в блокнот, включим перенос строк.



Можно разглядеть паттерн.

Для того, чтобы лучше разглядеть, единички заменяем на █, нолики — на ░:



Построим двухмерный график этой последовательности. На каждой следующей строчке $y$ последовательность сдвигается на $ky$ (где $k$ — целое число, константа) позиций влево. Перепишем $x^2$ как $(x+ky)^2$.

Для некоторых $ky$:

35:


661:


Больше примеров
64:


257:


274:


303:


443:


467:


468:


547:


548:


Мышкой по экрану


Для $(x+ky)^2$ можем раскрыть скобки, получим $x^2+2kxy+(ky)^2$. Получили уравнение поверхности.

Дискретизация поверхностей с ненулевой кривизной.



Для дальнейших экспериментов запишем уравнение в более общем виде:

$z=a(x^2+bxy+cy^2)^d$



Точно так же, как мы дискретизировали линейную функцию, мы можем дискретизировать поверхности второго порядка. Для этого считаем $z$ для каждого $x$ и $y$, после чего умножаем $z$ на иррациональное число, отбрасываем дробную часть, проверяем четность целой части — $\lfloor z\sqrt {2} \rfloor \; (\textrm{mod} \; 2)$

Для $b=0, c=1, d=1$ наше уравнение принимает вид:

$z=a(x^2+y^2)$



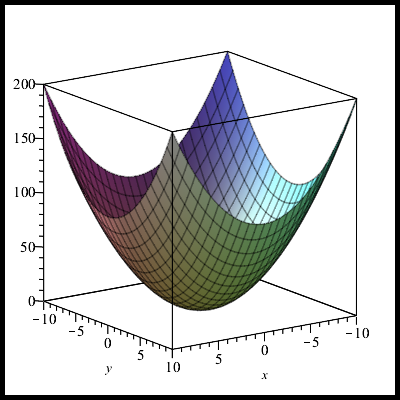
Это уравнение элиптического параболоида. Коэффициент $a$ определяет, насколько параболоид вытянут по оси $z$. Для $a=1$:



JavaScript 
for(var x=0;x<canvas.width;x++){
	xx=x-canvas.width/2;
	for(var y=0;y<canvas.height;y++){
		yy=y-canvas.height/2;
		z=a*(xx**2+b*xx*yy+c*(yy**2))**(d);
		if(Math.floor(z*Math.sqrt(2))%2) context.fillRect(x, y, 1, 1);
			
	}
}



Для $a=1/512$ получаем такой паттерн:



Можем этот же паттерн нарисовать недискретным. Вместо $\lfloor z\sqrt {2} \rfloor \; (\textrm{mod} \; 2)$ считаем $\sin(z\pi \sqrt {2})$. Значение функции масштабируем (прибавляем 1, умножаем на 128) и используем в качестве яркости пикселя:



Для $a=1/128$, дискретный и недискретный варианты:





При чем тут голография?
Паттерн, который мы получили — самая простая голограмма. Такой же паттерн мы получим, если сделаем срез сферической волны плоскостью. Или же срез плоской волны сферической поверхностью.



Коэффициент $c$ сжимает или растягивает паттерн по оси $y$. Для $c=2$ и $c=0.2$:





Коэффициент $b$ сжимает или растягивает паттерн по диагонали. Для $b=1.5$ и $b=-1.5$:





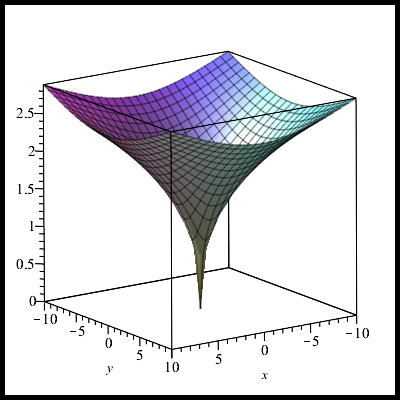
Дальше. Для $b=0, c=-1, d=1$ наше уравнение принимает вид:

$z=a(x^2-y^2)$



Это гиперболический параболоид — поверхность с отрицательной гауссовой кривизной:



Для $a=1/512$:



Для $a=1/128$:



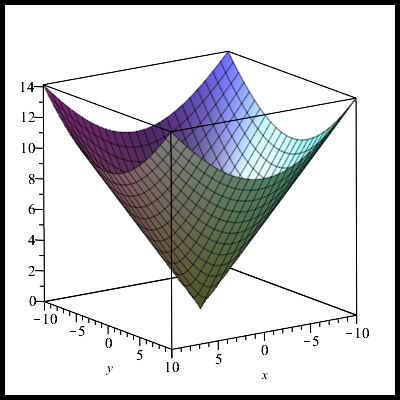
Попробуем поменять степень $d$. Для $b=0, c=1, d=1/2$ наше уравнение принимает вид:

$z=a\sqrt{x^2+y^2}$





Для $a=1/4$:



Для $a=2$:



Для $b=0, c=1, d=1/5$ наше уравнение принимает вид:

$z=a(x^2+y^2)^{1/5}$





Для $a=10$:



Для $a=100$:



Для $a=1000$:



Самые интересные паттерны получаются, если взять такое $d$, которое незначительно отличается от 1. Например для $b=0, c=1, d=1.01$:

Для $a=1/512$ паттерн похож на тот, что мы видели для элиптического параболоида:



Для $a=511/323$:



Еще несколько примеров:

$b=0, c=1, d=1.01, a=508/325$:



$b=0, c=1, d=1.01, a=389/489$:



$b=0, c=1, d=0.999, a=500/357$:



$b=0.01, c=1.01, d=1.01, a=159/202$:



$b=1.01, c=1.01, d=1.01, a=511/328$:



$b=1, c=1, d=1.01, a=459/291$:



Поиграться
В динамике — дискретные паттерны. Двигаем мышкой по экрану. Параметры $b, c, d$ вводим вручную. Параметр $a=x/y$ вычисляется из координат мышки.
В статике — можем посмотреть дискретный и недискретный паттерны.


Подводя итоги...



Мы попробовали дискретизировать линейную функцию и получили фрактал. Если сделать срез трехмерной плоской волны поверхностью с ненулевой кривизной — получим голографический паттерн. Интересно, что мы получим, если сделаем срез четырехмерной плоской волны пространством с ненулевой кривизной? Об этом поговорим в другой раз.

Комментарии (14)


  1. abcdsash
    28.05.2022 11:26
    #24385964
    +8

    ничего не понятно, но очень интересно )


  1. kovserg
    28.05.2022 11:55
    #24386028
    +1

    Вот такие формулы глаз радуют больше
    www.shadertoy.com/view/WsSBzh
    www.youtube.com/watch?v=8--5LwHRhjk


    1. amarao
      28.05.2022 18:24
      #24386690
      +3

      Стейк вкуснее ваших шейдеров.

      // аргумент примерно такого же уровня. Человек про одно, вы про совершенно что-то несвязное с этим.


  1. e-zig
    28.05.2022 14:01
    #24386256

    Прокрутка сих картинок весьма показательный тест частоты обновления экрана смарта. Между 60 и 120 Гц разница очень заметна.


  1. Browning
    28.05.2022 20:30
    #24386948

    Симпатично, но странно, что ни разу не прозвучало словосочетание "последовательность Битти".


  1. riky
    28.05.2022 22:03
    #24387180
    +2

    а еще вместо mod 2 можно сделать mod 256 и получить rgb картинки


    1. xcont Автор
      29.05.2022 10:31
      #24387978

      Достаточно сделать mod 3.

      После чего:

      if(z==0) context.fillStyle = 'rgb(255,0,0)';
if(z==1) context.fillStyle = 'rgb(0,255,0)';
if(z==2) context.fillStyle = 'rgb(0,0,255)';








      Здесь: rgb


      1. kovserg
        29.05.2022 10:48
        #24388008

        Картинки будут значительно красочнее если использовать не rgb а HSL


        1. xcont Автор
          29.05.2022 13:28
          #24388332

          Три варианта — дискретный (через mod 2), недискретный (через sin) и hsl:







          Здесь: hsl


          1. xcont Автор
            29.05.2022 13:39
            #24388356

            rgb с теми же параметрами:


  1. Chupaka
    28.05.2022 23:40
    #24387342

    Муар — это тоже фрактал, получается?

    З.ы. В заголовке как будто не хватает то ли "что" в начале, то ли "ничего" в конце...


    1. iShrimp
      30.05.2022 12:27
      #24391002

      Применительно к теме статьи, муар возникает в результате алиасинга - из-за того, что компьютер вычисляет функцию, имеющую высокие частоты, не во всех точках плоскости, а по дискретной сетке. Все эти кольца, кроме центральных, являются артефактами семплирования.

      В природе таких паттернов не существует, так как нет дискретных сеток, а есть сплошная непрерывная (до уровня молекул) среда. Если мы возьмём ту же функцию sin(a(x²+y²)) и построим её график со сглаживанием, то получим кольца Ньютона, которые на периферии, по мере удаления от центра, просто сливаются в однородный фон.


      1. Browning
        30.05.2022 12:54
        #24391122
        +1

        Зато на уровне молекул муар проявляется. Среди физиков, изучающих графен и другие двумерные кристаллы, в последние годы все очень интересуется муаром, потому что там происходит всякие неожиданные вещи.


  1. saduga
    30.05.2022 17:32
    #24392272

    Интересно написано про фракталы https://sunandstuff.com/mandelbrot/about/