Как оптимизировать данные с помощью TensorFlow

Чем больше данных, тем лучше, но слишком большое число признаков может оказаться неэффективным в плане повышения интерпретируемости или производительности. Материалом о возможном решении от доктора Роберта Кюблера делимся к старту флагманского курса по Data Science.
Посмотрите на код ниже:
import numpy as np
np.random.seed(0)
X = np.random.randn(1000, 900)
y = 2*X[:, 0] + 1 + 0.1*np.random.randn(1000)Здесь создаётся набор данных (X, y) из 1000 выборок и 900 признаков x₀, …, x₈₉₉ в каждой. Задача — установить истинность выражения y = 2x₀ + 1. Погрешность малая, а значит, линейная регрессия должна достигнуть значения r², близкого к 1. И вот что получается после перекрёстной проверки:
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score
print(cross_val_score(LinearRegression(), X, y))
# Output:
# [0.88558154 0.87775961 0.87564832 0.86230888 0.8796105 ]Значение r² на неохваченных данных равно ~0,87. Это довольно далеко от 1. Проблема ещё очевиднее, когда при таком же анализе модель ограничена первым десятком переменных:
print(cross_val_score(LinearRegression(), X[:, :10], y))
# Output:
# [0.99701015 0.99746395 0.99780414 0.99752536 0.99745693]Сокращение количества признаков повышает производительность модели до ~0,997%, а значит, признаки способны заполонить даже такой простой алгоритм, как линейная регрессия. И вот самые популярные способы уменьшить количество признаков:
простое удаление части признаков по некоторому правилу, например через одномерный анализ (корреляцию с целевым y) или оценка значимости (имеется в виду p-значение, важность признаков из древовидных алгоритмов, значения Шепли и т. д.);
метод главных компонент (далее — PCA), где с помощью специального линейного отображения (умножения матрицы данных X на другую матрицу W) данные преобразуются в пространство с меньшей размерностью. Обратите внимание: здесь не нужен
y.
Здесь рассмотрим ещё один способ, где PCA как будто обобщается — PCA на основе ядра. Конечно, я шучу! И говорю я об автоэнкодерах, хотя PCA на основе ядра — допустимый вариант.
Автоэнкодеры
Данные часто избыточны, но избыточность легко сокращается без больших потерь информации. Представьте набор данных с такими признаками:
высота в сантиметрах;
высота в метрах.
Оба признака содержат одну и ту же информацию, но если шум у признаков разный, то производительности модели это повредит, поэтому лучше выбрать только один признак.
Этот случай очевиден, но автоэнкодеры находят и сокращают и не столь очевидную избыточность: мы надеемся на то, что в информационном узком месте, в латентном пространстве, фильтруется только избыточная, а не важная информация. Проверить это можно просмотром ошибки восстановления между всеми x и x’.
Определение
Математическое определение автоэнкодера мне найти не удалось, но я помогу достаточно хорошо в нём разобраться. Автоэнкодер состоит из двух функций — это e — encoder и d — decoder:
e принимает наблюдение x из n признаков и сопоставляет его с вектором z размером m ≤ n. Вектор z называют скрытым вектором x.
d принимает скрытый вектор z и выводит x’ с размерностью n.
Нужно, чтобы x и x’ были близки, до x ≈ x’. Ошибка восстановления должна быть небольшой:
Необработанное наблюдение x в энкодере сокращается, а в декодере — распаковывается. При упаковке и распаковке сильного искажения x в среднем не должно быть:
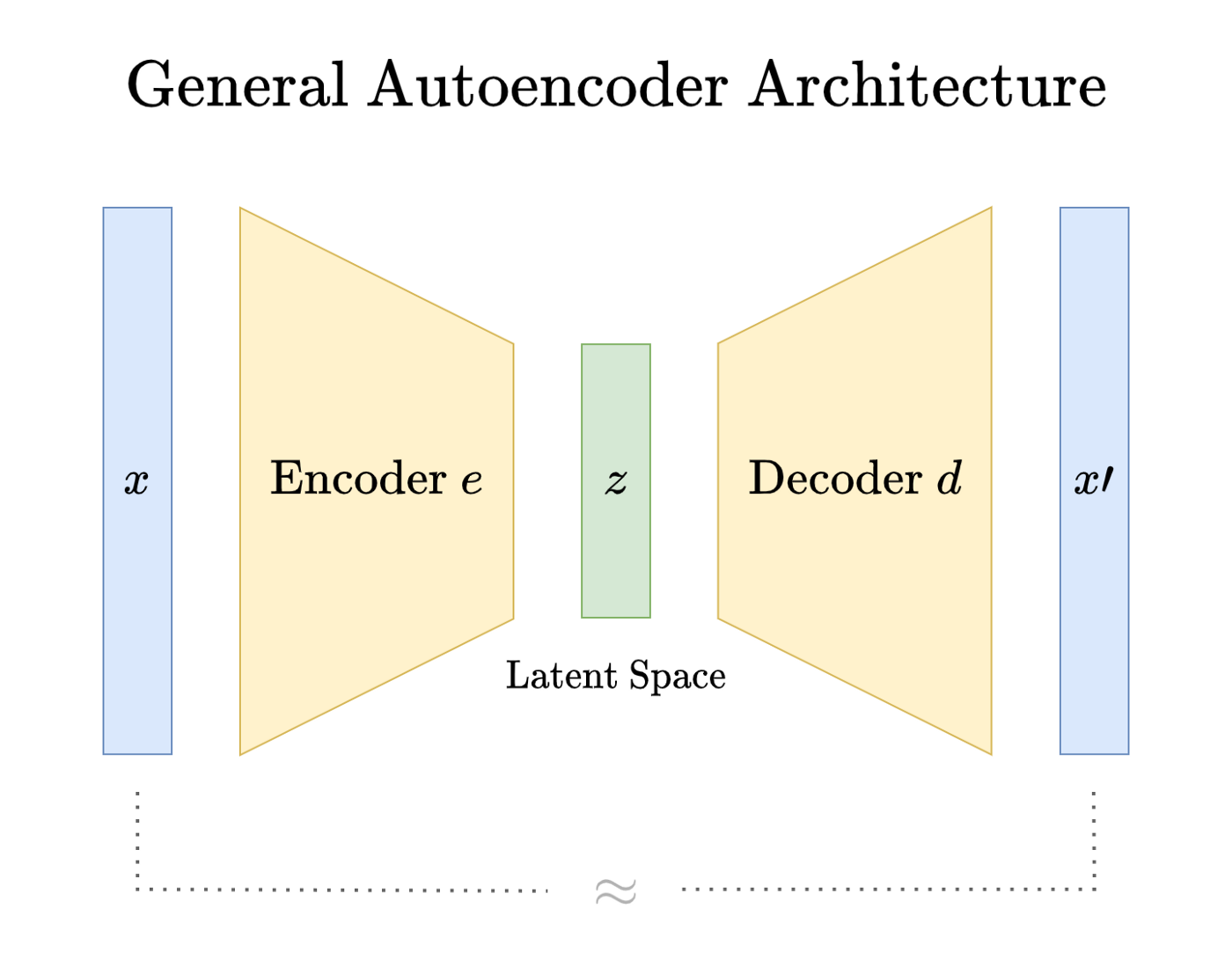
То же самое достигается в архивных форматах zip и rar, но с условием x = x’. Форматы сжатия jpeg и mp3 — с потерями, но они достаточно хороши, чтобы люди не видели разницы, по крайней мере, когда сжатие не очень агрессивное, т. е. не слишком мало значение m.
Зачем это нужно?
Итак, слишком много признаков — это, возможно, не всегда хорошо, а мы говорили о способности PCA сократить их количество. Но PCA — линейное преобразование, его выразительность ограничена. Вспомним, как работает метод.

Внизу слева показаны кодировки (вместо двух измерений здесь одно), а в нижнем правом — декодировки, в исходных двух измерениях. Оба верхних изображения показывают необработанные входные данные.
Если данные близки к линейному подпространству, то есть к линии, плоскости или гиперплоскости с размерностью m, то PCA с m компонентами работает очень хорошо.
Если это не так, в исходных данных теряется много информации:
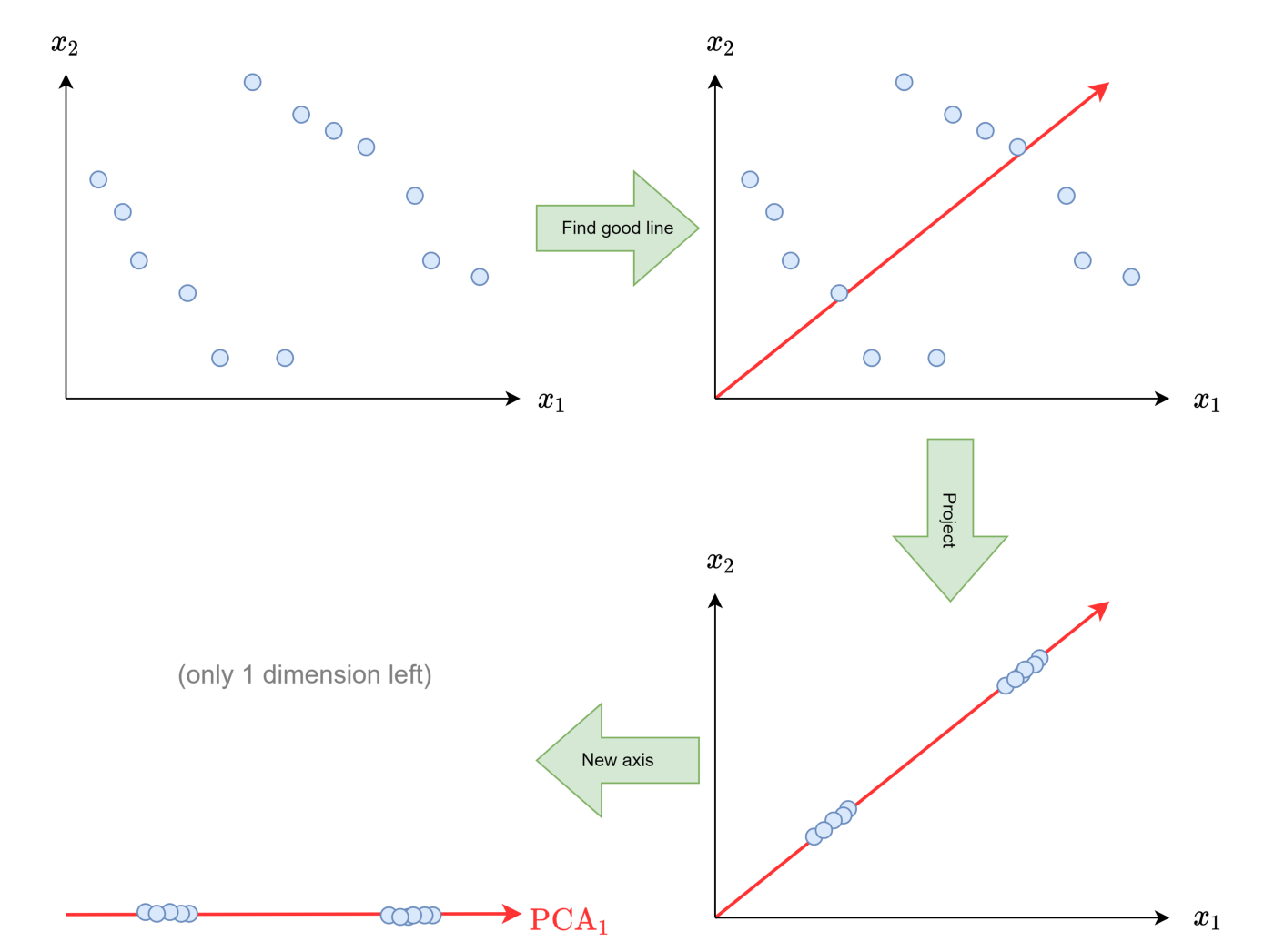
Если простота линейных преобразований — узкое место, то применим энкодеры и декодеры посложнее! Сделать это проще с помощью нейросетей.
Обычно речь идёт о нейросетевых автоэнкодерах, но ими выбор не ограничивается: с энкодерами и декодерами возможно всё. Например, по ссылке вы ознакомитесь с экзотическим автоэнкодером на основе деревьев решений, а здесь поработаем с традиционными автоэнкодерами.
Автоэнкодер на Tensorflow
Определим набор данных X с 4 признаками:
import tensorflow as tf
tf.random.set_seed(0) # keep things reproducible
Z = tf.random.uniform(shape=(10000, 1), minval=-5, maxval=5)
X = tf.concat([Z**2, Z**3, tf.math.sin(Z), tf.math.exp(Z)], 1)После этого возникают вопросы:
Как и до скольких измерений можно сократить X?
Что необходимо для восстановления X с меньшим числом признаков?
Здесь нужен единственный признак — это Z. X не содержит больше информации, чем Z, а получить признаки X можно после применения определённой функции к Z.
С помощью энкодера можно было бы понять, как найти обратный порядок функций, т. е. попасть из x = (z², z³, sin(z), exp(z)) в z. Декодер можно научить принимать число z и преобразовывать его обратно в x’ = (z², z³, sin(z), exp(z)).
Заметили вот это можно было бы? Это было бы очевидным решением, потому что мы знаем, как X генерируется из Z. Но в автоэнкодере это не очевидно; может быть найден другой способ сокращения данных, например x = (z², z³, sin(z), exp(z)) в z - 3. А декодер можно с тем же успехом научить декодировать это.
Теперь мы сможем создать работоспособный автоэнкодер с одним-единственным скрытым измерением:
class AutoEncoder(tf.keras.Model):
def __init__(self):
super().__init__()
self.encoder = tf.keras.Sequential([
tf.keras.layers.Dense(100, activation='relu'),
tf.keras.layers.Dense(100, activation='relu'),
tf.keras.layers.Dense(100, activation='relu'),
tf.keras.layers.Dense(1), # compress into 1 dimension
])
self.decoder = tf.keras.Sequential([
tf.keras.layers.Dense(100, activation='relu'),
tf.keras.layers.Dense(100, activation='relu'),
tf.keras.layers.Dense(100, activation='relu'),
tf.keras.layers.Dense(4), # unpack into 4 dimensions
])
def call(self, x):
latent_x = self.encoder(x) # compress
decoded_x = self.decoder(latent_x) # unpack
return decoded_x
tf.random.set_seed(0) # keep things reproducible
ae = AutoEncoder()
ae.compile(
optimizer=tf.keras.optimizers.Adam(learning_rate=0.0001),
loss='mse'
)
ae.fit(
X, # input
X, # equals output
validation_split=0.2, # prevent overfitting
epochs=1000,
callbacks=[
tf.keras.callbacks.EarlyStopping(patience=10) # early stop
]
)
# Output:
# ...
# Epoch 69/1000
# 250/250 [==============================] - 0s 1ms/step - loss: # 0.0150 - val_loss: 0.0276Модель можно обучить лежащей в основе цифр структуре! И проверить максимальную ошибку в автоэнкодере:
print(tf.reduce_max(tf.math.abs(X-ae(X))))
# Output:
# tf.Tensor(0.89660645, shape=(), dtype=float32)Неплохо, если учесть, что некоторые признаки исчисляются сотнями. А теперь сделаем кое-что поинтереснее.
Сжатие чисел
Возьмём MNIST — классический набор данных рукописных цифр:
(X_train, _), (X_test, _) = tf.keras.datasets.mnist.load_data()
X_train = X_train.reshape(-1, 28, 28, 1) / 255. # value range=[0,1]
X_test = X_test.reshape(-1, 28, 28, 1) / 255. # shape=(28, 28, 1)Изобразим несколько чисел:
import matplotlib.pyplot as plt
for i in range(3):
plt.imshow(X_train[i])
plt.show()

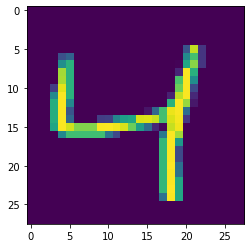
Набор данных состоит из рукописных цифр 28 x 28 пикселей. Каждый пиксель — признак, поэтому у нас набор данных 28 * 28 = 784 размерности. Это очень мало для набора данных с изображениями.
Теперь создадим для этого набора автоэнкодер. Но почему вообще он должен получиться Рукописные цифры — это очень малая часть всевозможных изображений размером 28 x 28 пикселей. У цифр весьма специфическая пиксельная конфигурация. Например, следующие изображения 28 x 28 — это никак не цифры:
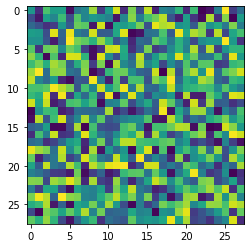
Но сколько измерений нужно, чтобы выразить MNIST? К сожалению, общего ответа на этот вопрос нет. Чтобы декодирование было достаточно хорошим, обычно стремятся к меньшей размерности. Создадим другой простой автоэнкодер прямого распространения, но со свёрточными слоями. Перейдём сразу к делу.
Обратите внимание: значения пикселей изображений варьируются от 0 до 1 — так обучение быстрее и стабильнее, а форма отдельного изображения (28, 28, 1) предназначена для работы свёрточных слоёв:
from tensorflow.keras import layers
class ConvolutionalAutoEncoder(tf.keras.Model):
def __init__(self):
super().__init__()
self.encoder = tf.keras.Sequential([
layers.Conv2D(4, 5, activation='relu'),
layers.Conv2D(4, 5, activation='relu'),
layers.Conv2D(1, 5, activation='relu'),
])
self.decoder = tf.keras.Sequential([
layers.Conv2DTranspose(4, 5, activation='relu'),
layers.Conv2DTranspose(4, 5, activation='relu'),
layers.Conv2DTranspose(1, 5, activation='sigmoid'),
])
def call(self, x):
latent_x = self.encoder(x)
decoded_x = self.decoder(latent_x)
return decoded_x
tf.random.set_seed(0)
ae = ConvolutionalAutoEncoder()
ae.compile(optimizer='adam', loss='bce')
ae.fit(
X_train,
X_train,
batch_size=128,
epochs=1000,
validation_data=(X_test, X_test),
callbacks=[
tf.keras.callbacks.EarlyStopping(patience=1)
]
)
# Output:
# ...
# Epoch 12/1000
# 469/469 [==============================] - 91s 193ms/step - loss: # 0.0815 - val_loss: 0.0813Посмотрим, насколько велико скрытое пространство:
print(ae.summary())Форма на выходе для первого слоя, энкодера (None, 16, 16, 1), означает выходные данные 16 * 16 * 1 = 256 размерности и может быть интерпретирована как изображение размером 16 x 16 пикселей с одним каналом.
В обучении применяется bce (бинарная кросс-энтропия), при которой в модели выводятся значения, близкие к 0 или 1. Поэтому в последнем слое декодера используется также сигмоидальная функция активации. Из-за применения MSE многие пиксели часто имеют значения около 0,5.
Прежде чем продолжить, проверим восстановление изображений вручную:
decoded_images = ae.predict(X_test[:10])
latent_images = ae.encoder(X_test[:10])
plt.figure(figsize=(20, 4))
for i in range(10):
ax = plt.subplot(3, n, i + 1)
plt.imshow(X_test[i])
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
ax = plt.subplot(3, n, i + 1 + n)
plt.imshow(latent_images[i] / tf.reduce_max(latent_images[i]))
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
ax = plt.subplot(3, n, i + 1 + 2*n)
plt.imshow(decoded_images[i])
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()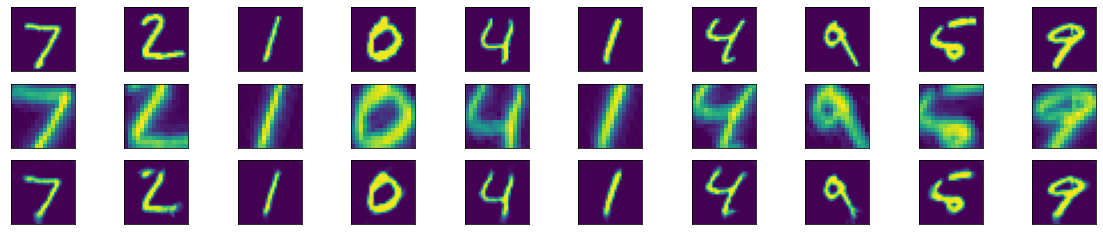
В целом выглядит прилично! Кое-где есть проблемы, например с двойкой, но сетевая архитектура может сделать её получше. Скрытые версии исходных изображений по-прежнему очень похожи на исходные цифры, только с разрешением: 16 x 16 пикселей, а не 28 x 28. Так случается не всегда. В автоэнкодере такое сжатие считается хорошим.
Я нахожу интересным обучение автоэнкодера тому, что границы изображений не содержат полезной информации: автоэнкодер просто увеличивает масштаб изображений цифр — так, что ими заполняется всё изображение. Как человек я, наверное, тоже сделал бы так, а здесь случилось небольшое совпадений.
Другие архитектуры
Мы видели классический и свёрточный автоэнкодеры. Наверное, вы уже догадались: меняя структуру автоэнкодера, также можно создавать автоэнкодеры долгой кратковременной памяти (LSTM) или автоэнкодеры типа «последовательность-в-последовательности», автоэнкодеры-трансформеры и многие другие.
Разреженные автоэнкодеры штрафуются при одновременном применении слишком большого числа скрытых измерений. Делается это за счёт добавления к слою (слоям) регуляризатора активности через activity_regularizer.
Но основная идея всегда одна и та же: уменьшить входные данные и снова сделать их как можно больше, как в криминальном сериале (это реально!):

Ещё один стóящий автоэнкодер, который мне очень нравится, — вариационный энкодер. Он способен не только восстанавливать, но и создавать данные:

Заключение
Данные могут обладать большой избыточностью, поэтому на их обработку требуется больше памяти и вычислительной мощности, а производительность моделей может снизиться. Дело часто ограничивается удалением части признаков или применением таких методов, как PCA.
Но эти методы могут оказаться слишком простыми, они не подходят для корректного извлечения информации из данных; эту проблему могут решить автоэнкодеры, где данные кодируются до нужной сложности.
Теперь вы можете сами изучать автоэнкодеры, экспериментировать, извлекать из них пользу для своих задач и делать это с удовольствием. Надеюсь, сегодня вы узнали что-то новое, интересное и полезное. Спасибо за внимание!
А мы поможем вам прокачать навыки или с самого начала освоить профессию, востребованную в любое время:
Выбрать другую востребованную профессию.


