В этой небольшой статье мы сравним следующие реализации быстрого преобразования Фурье (БПФ) для платформы .NET:
| Accord | Exocortex | Math.NET | NWaves | NAudio | Lomont | DSPLib | FFTW | |
| Версия: | 3.8.0 | 1.2 | 5.0 | 0.9.6 | 2.1 | 1.1 | (2017) | 3.3.9 |
| Лицензия: | LGPL | BSD | MIT | MIT | MIT | - | MIT | GPL |
| Сборки: | 3 | 1 | 1 | 1 | 1 | - | - | 1+1 |
| Размер: | 3.6 MB | - | 1.6 MB | 0.3 MB | 0.2 MB | - | - | 2.3 MB |
| NuGet: | да | нет | да | да | да | нет | нет | нет |
▍ Примечания об испытуемых
- Accord.NET – это фреймворк машинного обучения, включающий в себя обработку аудио и изображений. На данный момент его разработка прекращена.
- Проект Exocortex был запущен вначале существования .NET 1.0. Его копия, приведённая в этой статье, была обновлена под целевой стандарт .NET 2.0 и использование типа
Complexиз пространства имёнSystem.Numerics. - NAudio использует кастомную реализацию типа
Complexс действительной и мнимой частями одинарной точности. - DSPLib – это небольшая библиотека для применения БПФ к вещественным числам и спектрального анализа. Обратное преобразование в ней не реализовано.
- FFTW – это популярная нативная реализация БПФ. Она является, пожалуй, самым быстрым опенсорс решением, какое можно найти в сети, так что её сравнение с управляемым кодом будет не совсем честным. Но мне всё же было любопытно узнать, какой получится результат.
Исполняемые файлы FFTW к статье не прилагаются. Если вы захотите включить эту реализацию в бенчмарк, файлы fftw3.dll и fftw3f.dll нужно будет скачать вручную. Для получения свежей версии можете использовать Conda или посетить проект на GitHub.
▍ Ресурсы
▍ Бенчмарк
В особенности меня интересовало одномерное быстрое преобразование Фурье для вещественных входных значений (обработки аудио). Приведённый ниже интерфейс использовался для всех тестов. Если у вас есть собственная реализация БПФ, то вы вполне можете встроить её в бенчмарк, реализовав этот интерфейс и инстанцировав тест в методе
Util.LoadTests().interface ITest
{
/// <summary>
/// Получаем название теста.
/// </summary>
string Name { get; }
/// <summary>
/// Получаем размер теста БПФ.
/// </summary>
int Size { get; }
/// <summary>
/// Получаем или устанавливаем значение, указывающее, нужно ли запускать тест.
/// </summary>
bool Enabled { get; set; }
/// <summary>
/// Подготавливаем данные для обработки БПФ.
/// </summary>
/// <param name="data">Массив образцов.</param>
void Initialize(double[] data);
/// <summary>
/// Применяем к данным БПФ.
/// </summary>
/// <param name="forward">Если false, применяем обратное БПФ.</param>
void FFT(bool forward);
// Игнорируем бенчмарк (используется только для 'FFT Explorer', см. следующий раздел).
double[] Spectrum(double[] input, bool scale);
}Для лучшего понимания правильной реализации интерфейса взгляните на разные тесты в пространстве имён
fftbench.Benchmark проекта fftbench.Common.Exocortex, Lomont и FFTW имеют особые реализации для вещественных данных, и их код вполне может оказаться где-то вдвое быстрее стандартной реализации для комплексных чисел.
Accord.NET, Math.NET и FFTW поддерживают входные массивы любого размера (т.е. размер не должен быть кратным 2).
▍ Результаты
Ниже показан вариант вывода при выполнении консольного приложения fftbench. В первом столбце отражена относительная скорость в сравнении с Exocortex (real):
$ ./fftbench 10 200
FFT size: 1024
Repeat: 200
[14/14] Done
FFTWF (real): 0.2 [min: 1.29, max: 1.64, mean: 1.33, stddev: 0.03]
FFTW (real): 0.2 [min: 1.34, max: 1.60, mean: 1.43, stddev: 0.05]
FFTW: 0.5 [min: 2.86, max: 3.13, mean: 2.87, stddev: 0.03]
Exocortex (real): 1.0 [min: 5.72, max: 6.20, mean: 5.76, stddev: 0.05]
Lomont (real): 1.1 [min: 6.12, max: 8.04, mean: 6.26, stddev: 0.17]
NWaves (real): 1.5 [min: 8.44, max: 10.73, mean: 8.52, stddev: 0.24]
NWaves: 1.7 [min: 9.70, max: 11.90, mean: 9.79, stddev: 0.21]
Exocortex: 1.9 [min: 10.56, max: 12.93, mean: 10.71, stddev: 0.22]
Lomont: 1.9 [min: 10.58, max: 15.90, mean: 10.77, stddev: 0.38]
NAudio: 2.1 [min: 11.80, max: 14.17, mean: 12.03, stddev: 0.20]
AForge: 2.6 [min: 14.72, max: 15.90, mean: 14.93, stddev: 0.12]
DSPLib: 2.8 [min: 15.30, max: 22.10, mean: 15.91, stddev: 0.94]
Accord: 3.8 [min: 21.06, max: 29.19, mean: 21.69, stddev: 0.93]
Math.NET: 7.4 [min: 38.26, max: 73.53, mean: 42.74, stddev: 4.60]
Timing in microseconds.В этом тесте каждое БПФ по факту вызывается 50 * 200 раз (число повторений получается путём умножения второго аргумента командной строки, 200, на предустановленное число внутренних итераций, 50). Размер БПФ равен 2^10 (первый аргумент командной строки). Бенчмарк выполнялся на процессоре AMD Ryzen 3600.
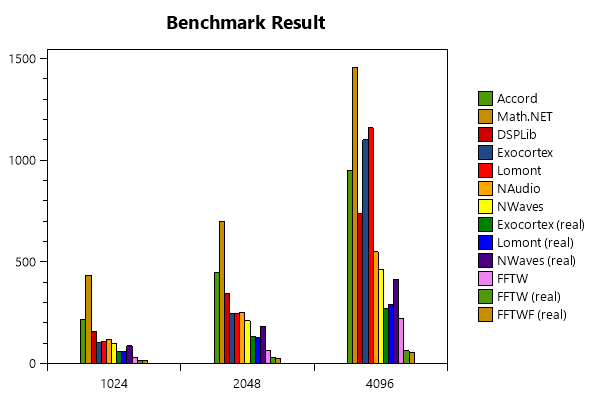
На диаграмме ниже показаны результаты теста для разных БПФ с размером 1024, 2048 и 4096. Здесь использовалось приложение fftbench-win с 200 повторениями:

▍ Интерпретация результатов
Приложение fftbench-win (проект WinForms включён только в скачиваемые ресурсы статьи, на GitHub его нет) содержит утилиту FFT Explorer. Для её запуска кликните по левой крайней иконке в окне бенчмарка.
FFT Explorer позволяет выбирать реализацию БПФ, входной сигнал и размер БПФ. На трёх графиках будет показан входной сигнал, вычисленный выбранным алгоритмом спектр и сигнал, полученный обратным преобразованием Фурье.
Рассмотрим пример сигнала, сгенерированного классом
SignalGenerator. Это простая синусоида с частотой 1Гц и амплитудой 20.0:public static double[] Sine(int n)
{
const int FS = 64; // частота дискретизации
return MathNet.Numerics.Generate.Sinusoidal(n, FS, 1.0, 20.0);
}Пусть размер кадра БПФ будет n = 256. При частоте дискретизации 64Гц наш периодический сигнал повторится в заданном окне ровно четыре раза. Имейте в виду, что все значения выбраны из соображения точной согласованности между периодом сигнала, частотой дискретизации и размером БПФ. Это сделано, чтобы избежать просачивания спектральных составляющих.
Каждый отсчёт (bin) вывода БПФ отделяется шагом частотного разрешения (частота дискретизации / размер БПФ), который в нашем случае составляет 64/256 = 0.25. Следовательно, мы ожидаем, что пик, соответствующий нашему сигналу 1Гц, будет находиться в отсчёте 4 (поскольку 1.0 = 4 * 0.25).

В силу специфики ДПФ спектр сигнала будет масштабирован на n = 256, поэтому при отсутствии дальнейшего масштабирования мы ожидаем значение 20.0 * 256 / 2 = 2560. На два мы делим, так как амплитуда распределяется между двух отсчётов. Второй отсчёт расположен по индексу 256 – 4 = 252 и будет иметь ту же величину, поскольку при вещественных входных сигналах вывод БПФ, оказывается, (сопряжён) симметричен (относительно n/2, отсчёта, соответствующего частоте Найквиста).
Фактическое значение пика не будет согласовываться между разными реализациями БПФ ввиду отсутствия общего соглашения о масштабировании. Если размер БПФ равен n, то некоторые реализации масштабируют БПФ на 1/n, другие масштабируют на 1/n обратное БПФ, третьи масштабируют оба БПФ на 1/sqrt(n), а некоторые вообще масштабирование не делают, например, FFTW.
В таблице показаны амплитуды, вычисленные разными реализациями БПФ для вышеприведённого примера:
| Accord.NET | Exocortex.DSP | Math.NET | NAudio | NWaves | Lomont | DSPLib | FFTW | |
| Значение: | 2560 | 2560 | 160 | 10 | 2560 | 160 | 10 | 2560 |
Здесь мы видим, что NAudio и DSPLib масштабируют на 1/n, а Math.NET и Lomont на 1/sqrt(n) (и Math.NET, и Lomont позволяют пользователю менять условия масштабирования; в бенчмарке использовались установки по умолчанию).
▍ Выводы
Вполне ожидаемо, что явным победителем стала FFTW. Так что, если использование нативной библиотеки под лицензией GPL вам подходит, то выбирайте её. В случае управляемого кода мы видим, что неплохо работает NWaves. И Exocortex, и Lomont отлично справляются с небольшими БПФ, но с увеличением размера производительность падает. А вот с обработкой вещественных сигналов те же Exocortex и Lomont справились вообще без проблем, даже при больших размерах.
▍ История
- 2016-05-15 – начальная версия;
- 2016-06-14 – добавлена информация, которую просили в комментариях;
- 2018-09-02 – обновлены библиотеки, включена DSPLib и исправлен бенчмарк (спасибо участнику I'm Chris);
- 2022-07-02 – обновлены библиотеки, добавлена NWaves и ссылка на проект SharpFFTW/fftbench.

Комментарии (10)

orland
09.07.2022 05:11+2А можно на КДПВ добавить подпись к оси Y или словами как-то сказать, что чем больше значение - тем хуже. Пришлось досмотреть до конца статьи, чтобы это понять. Или так задумано?

Chonkoacha
09.07.2022 05:12Я конечно не разбираюсь в тестах, но эти xml комментарии к каждому свойству по мне уж лишние

Aleshonne
09.07.2022 11:36Ни разу не возникало мысли ради простого одномерного БДПФ тянуть в проект новую зависимость. Алгоритм Кули - Тьюки реализуется в 20 строк, элементарным образом параллелится, а время его работы составляет несколько процентов от времени, необходимого для вывода результата работы на экран. Безусловно, самописная реализация на F# окажется несколько менее эффективной, чем библиотеки, написанные профессионалами на C++, но, в моём случае (обработка сейсмических сигналов) на это можно смело наплевать.
Зато нельзя наплевать на то, что число отсчётов в сейсмограмме очень велико (несолько миллионов отсчётов — обычное дело) и почти никогда не оказывается степенью двойки, а шаг по времени для некоторых сценариев записи непостоянный (чем выше амплитуда, тем меньше шаг). Могут ли библиотеки работать с таким сигналом и если могут — то как конкретно они это делают, почти никто не пишет.

wilcot
10.07.2022 10:46Так-то и быструю сортировку можно написать в 10-20 строчек, но так обычно не делают. А все потому, что на самом деле эффективный алгоритм - это далеко не «наколеночное» решение.
В случае с FFT, то тут целый простор для улучшений и реализаций, начиная от поддержки произвольных длин, заканчивая локальными оптимизациями, поддержкой команд SSE, AVX и т.д. Скорее всего в реальном проекте (не лабораторной работе для студентов) вы не захотите тратить время на это все, а подключите тот же FFTW.
Разница сортировки и FFT в том, что сортировка уже встроена в поставляемую стандартную библиотеку, а FFT нет. Но это не повод для написания собственных реализаций. Конечно, все зависит от ситуации.

Aleshonne
10.07.2022 21:45В том то и прикол, что реализация БПФ с параллельностью, поддержкой произвольных длин и непостоянного шага по времени у меня заняла минут 15-20, что сравнимо со временем на поиск и подключение библиотеки в обычных условиях и в несколько десятков раз меньше, чем в условиях доступности только корпоративной сети. Там, конечно, нет SSE/AVX/ассемблера, и, при желании, скорость работы можно повысить раза в 2, но сейчас, как я уже писал выше, отрисовка итогового графика является гораздо более ресурсозатратной частью программы. Если когда-то в будущем в проект придётся тянуть тот же Math.NET, то станет иметь смысл использовать реализацию оттуда, а пока живём с велосипедом.

Bright_Translate Автор
09.07.2022 15:51+1Размер указан в MB. А здесь под assemblies не сборки подразумеваются? Тогда что, подскажите?
Why some assemblies/projects are marked as .Noncommercial in their names?
Some assemblies, such as Accord.Math.Noncommercial are marked as Noncommercial because they include algorithms that have been shared under academic-only licenses, or that otherwise contain patented algorithms for which would be necessary to acquire a license to commercialize. If you would are using the framework and plan to commercialize your product, please avoid linking your project against those specific assemblies (note: the assembly shown as an example is different from the standard Accord.Math assembly, which is perfectly OK to use in commercial applications).Разве не о разных сборках речь?


DistortNeo
На самом деле, потенциал .NET и близко не раскрыт.
Во-первых, FFTW использует многопоточность, во вторых — SIMD (в .NET его завезли, кстати).
При нормальной реализации .NET будет оставать не более, чем в 2 раза.
Правда, зачем изобретать велосипед, когда можно не мучиться и дёргать вызовы из FFTW.