Привет, чемпион!
Ребята с «вышкой» всё время умничают, что в Data Science нужна «математика», но стоит копнуть глубже, оказывается, что это не математика, а вышмат.
В реальной повседневной работе Data Scientist'а я каждый день использую знания математики. Притом очень часто это далеко не «вышмат». Никакие интегралы не считаю, детерминанты матриц не ищу, а нужные хитрые формулы и алгоритмы мне оперативнее просто загуглить.
Решил накидать чек-лист из простых математических приёмов, без понимания которых — тебе точно будет сложно в DS. Если ты только начинаешь карьеру в DS, то тебе будет особенно полезно. Мощь вышмата не принижаю, но для старта всё сильно проще, чем кажется. Важно прочитать до конца!
Дисклеймер: Сам я — человек с высшим образованием. Закончил бакалавриат и магистратуру Физтеха (последнее с отличием). Не буду с кем-либо спорить о том, нужен ли вышмат в работе Data Scientist'a. Просто покажу вам реальный список математических приёмов, которые я действительно часто использую в работе. Вы удивитесь, но рассчитывать вероятность достать чёрный шар из корзины мне не приходится. Я не выступаю против того, чтобы знать много и лишь хочу, чтобы получаемые знания были актуальными.
▍ Разогреваемся на простой математике
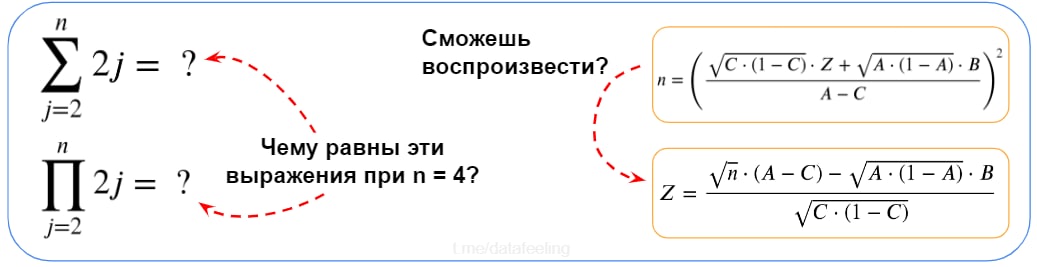
Если обозначения слева тебя не пугают и ты с лёгкостью расшифруешь их при чтении научных статей, а вывод справа ты воспроизведёшь даже с закрытыми глазами, то могу сказать, что ты уже на хорошем старте. Умение выражать одни переменные через другие и понимать математические обозначения — это базовый навык, без которого ты будешь часто застревать даже в рутинных задачах. Кстати, формулы редко бывают ещё сложнее, чем я привёл.
▍ Простые преобразования функций
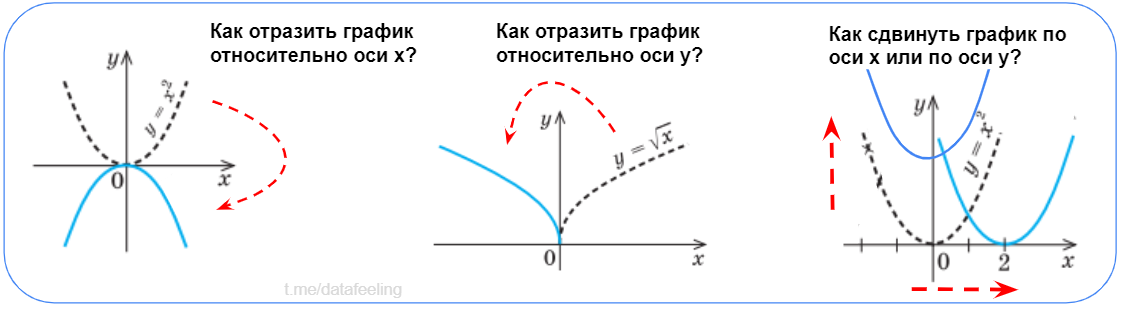
Если ты с ходу отвечаешь на эти вопросы, значит, ты точно не пропускал в школе уроки математики и легко умеешь отражать и смещать функции. Казалось бы, тут нет ничего сложного, но эти знания я часто использую при feature engineering'е или когда просто хочу понять, как ведёт себя некоторая функция.
▍ Сложные преобразования функций

Если не успело пройти и 5 секунд, а ты уже назвал в первом случае функцию логарифма, а во втором — сигмоиду в связке со сдвигом и растяжением, то ты точно уже на многое способен. Тогда различные преобразования данных в работе Data Scientist'а тебе покажутся детским лепетом.
▍ Нормирование данных
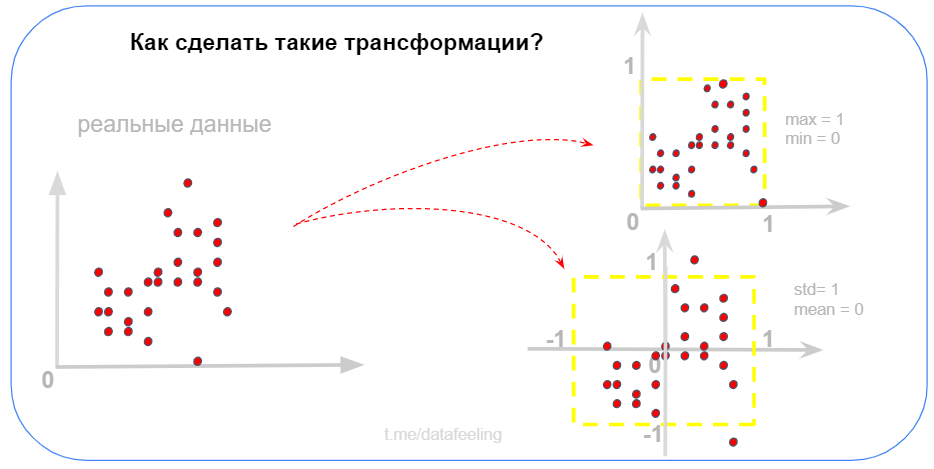
Пусть ты никогда и не слышал про Min-Max Scaling или Standart Scaling, но ты с ходу придумал, как превратить диапазон значений данных в интервал от 0 до 1, то я могу только сказать — «Браво!». А если ты при этом ещё и знаешь, как среднее выборки сделать нулём, а дисперсию — равной единице, то ты нереально хорош! Кстати, такие нормировки я делал ещё на уроках физики в школе, чисто на уровне логики. В реальной работе частенько приходится нормировать данные.
▍ Геометрия

Быстро ли ты вспомнил про Теорему Пифагора и формулу косинуса между двумя векторами?! Если для тебя не составило труда оперативно написать эти формулы, то смело прыгай в Data Science!
Казалось бы, зачем в Data Science знания из геометрии?! Однако, на практике эти знания дают тебе мощные инструменты и не только для информативного описания объектов новыми признаками, но и для понимания методов машинного обучения, таких как KNN, а с помощью формулы косинуса ты легко можешь решать такие задачи как face recognition или face verification и многие другие, где нужно сравнивать между собой многомерные объекты. В одном из соревнований по картинкам, мне очень пригодились эти знания.
▍ Ловим зависимости на фоне шума
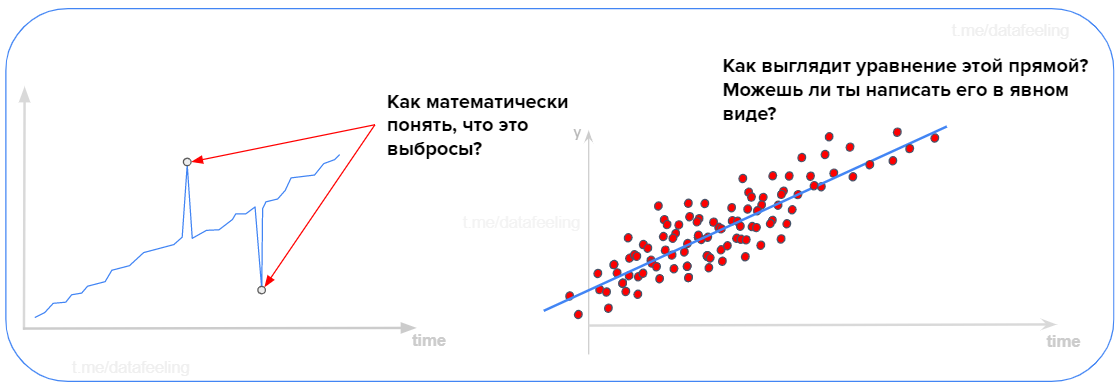
А в этот раз ты быстро справился? Пусть ты не знаешь ничего про p-value или что такое линейная регрессия, но если на этих вопросах у тебя как минимум закружилось в голове что-то про правило 3-х сигм или уравнение прямой а-ля y = kx + b, то поздравляю, у тебя есть хорошая начальная база. А вот если в твоей речи прозвучит ещё p-value и метод наименьших квадратов, то вряд ли бытовая рутина по очистке шумных данных в работе Data Scientist'а легко выбьет тебя из седла спокойствия.
▍ Статистики и распределения
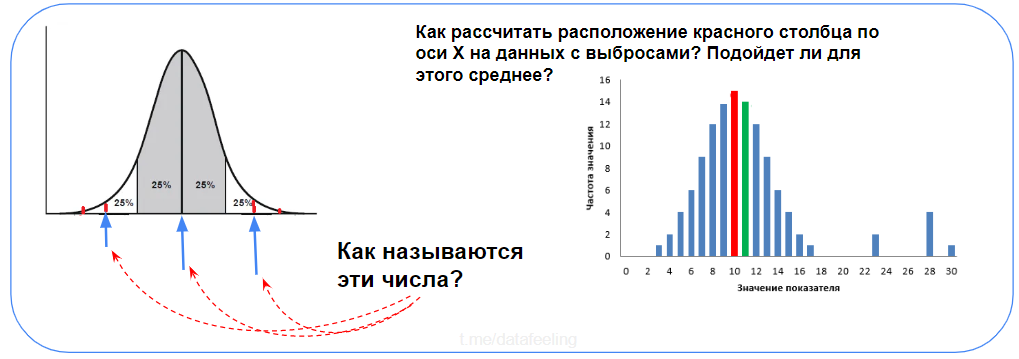
Опять лёгкие вопросы? Это хороший показатель!
Со школы я знал про медиану, но вот реальную её пользу почувствовал, только когда начал работать с реальными данными, в которых крайне редко нет выбросов или другого мусора. Чтобы понять её суть, достаточно вспомнить анекдот — «Когда Билл Гейтс заходит в бар, в среднем люди в баре становятся миллиардерами». Что касается квантилей и прочих статистик, они пригодятся тебе либо при работе со статистическими критериями и проверкой гипотез, либо, как минимум — при feature engineering’а на временных рядах, где такие квантильные фичи часто хорошо себя показывают.
▍ Виды распределений
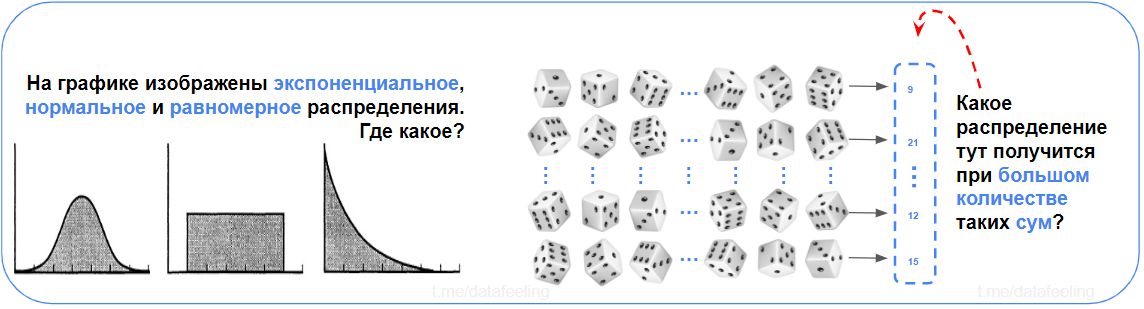
Просто? И ты даже не задумался и сразу выдал ответы? Нормальное распределение ты узнаешь из тысячи? А ЦПТ ты сформулируешь, даже если ночью разбудить? — Хорош, хорош!
Не помню, чтобы в школе или вузе случалось много опираться на распределения данных, но вот на реальных задачах в работе мне с таким сталкиваться приходится. Зная распределения и их свойства, твоя математическая интуиция при работе с реальными данными становится разрушительной силой. В вопросах проверок гипотез или уже пресловутого feature engineering'а тебе будет сильно проще.
▍ Преобразование распределений
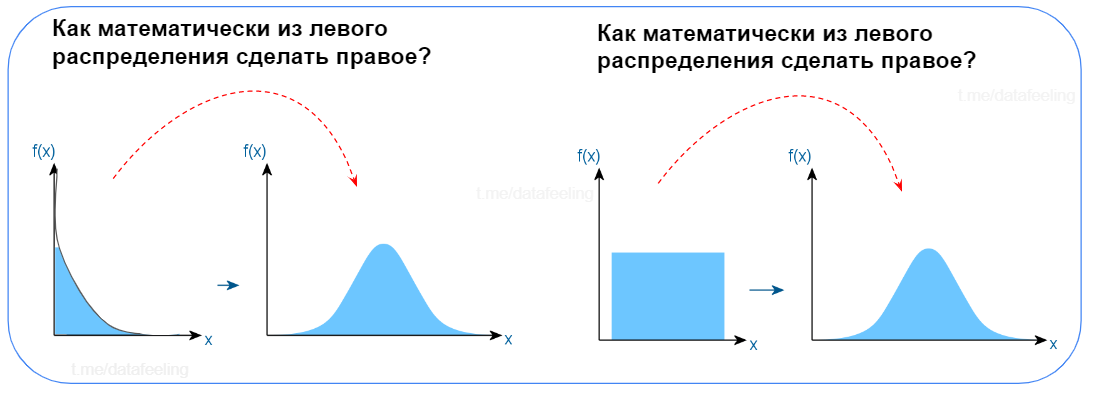
Легко? Или всё-таки задумался? Такими вопросами можно сбить с толку даже опытного Data Scientist'а. Вот тут даже мои коллеги задумаются, как провернуть такие математические финты. И если для левой ситуации многие предлагают логарифмирование, то правый случай запросто может вызвать синдром самозванца. А ведь это всё та же ЦПТ из предыдущего вопроса. В народе этот метод ещё называют бустрапом. Этот приём мне часто помогает при выравнивании распределений или увеличении чувствительности статистических критериев. Мощная штука. Бери на вооружение!
▍ Временные ряды
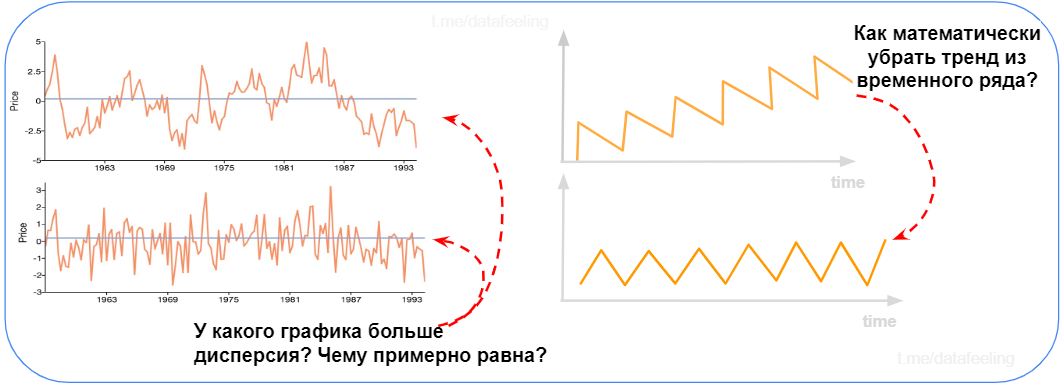
А как ты справился с этими задачами? Раз ты легко оперируешь такими понятиями, как дисперсия или квадратичное отклонение да ещё и визуально эти значения оцениваешь, то ты запросто осилишь и другие вещи по типу скользящих статистик и так далее. А чтоб убрать тренд в правом графике достаточно посчитать разницу между соседними точками ряда. При работе с временными рядами — это частая практика, до которой запросто догадаешься и без спец. курсов.
▍ Корреляция и зависимости
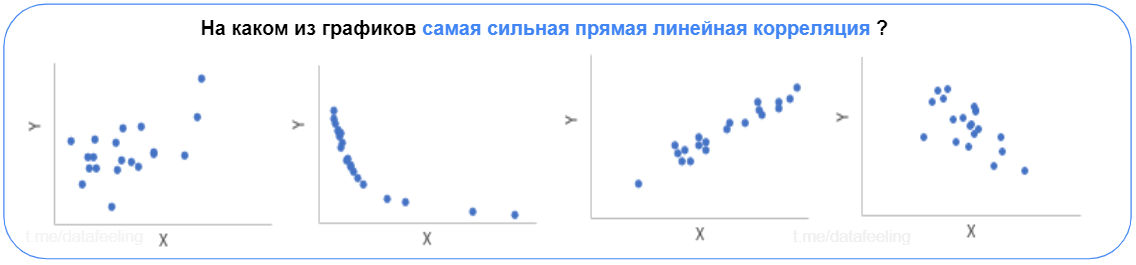
Ещё один навык, без которого тебе будет сложно — отделять “шумные” данные от “чистых”. «Шум» только мешает объяснить исследуемые эффекты или зависимости. Даже если ты не знаешь, что такое корреляция Пирсона и как её посчитать, но легко среди графиков выбираешь верный, то в целом — ты уже молодец. Ты сможешь без труда сориентироваться и объяснить, отчего в данных зависит целевая переменная. А разобраться в сложных формулах или заумных названиях это уже дело времени.
▍ Производные
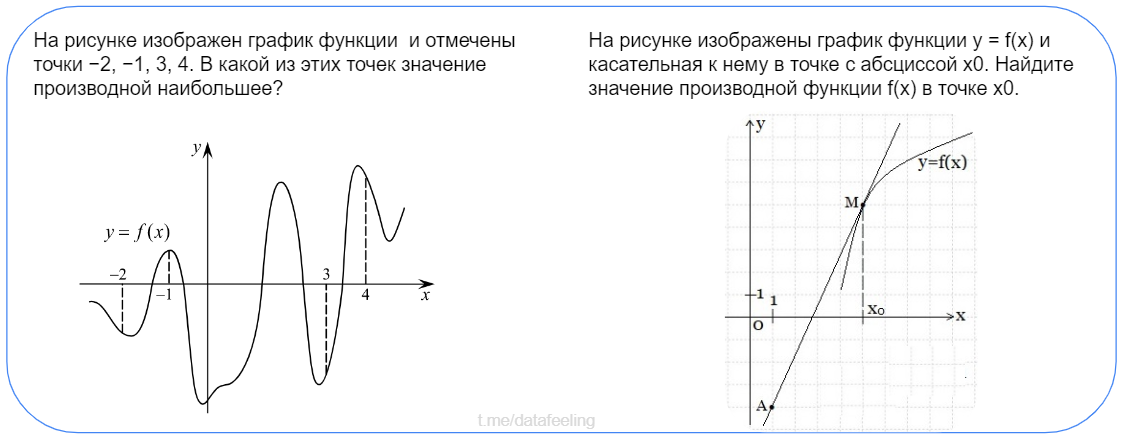
Тут уж, как бы я ни лукавил, в производных разобраться всё же надо бы. Займёт максимум один вечер, но зато на выходе сможешь сразу нырять в нейронки. И вообще, поймёшь, зачем и как минимизировать хотя бы простые функции. В случае многомерных функций, за тебя уже давно все написали и реализовали, надо только понять и выработать интуицию.
▍ Заключение и главный посыл статьи
В Data Science на практике нет неподъемной математики. Не надо тратить годы на изучение вышмата, чтобы просто начать работать в этой индустрии.
Да, без более глубокой базы — тебе будет иногда сложно что-то понять или пройти собеседование. Однако стажировки и соревнования имеют порог входа в разы ниже.
Да, соревноваться с лидерами индустрии или другими кандидатами с большим опытом будет поначалу непросто, но и у тебя рано или поздно при должном усердии накопится опыт и разовьются навыки.
Да, на высоких оборотах ресёрча надо глубоко погружаться в сложные вещи. А будешь ли ты вообще в реальности заниматься исследованиями, и руками имплементировать сложные математические концепции из статей? Что если тебе вообще больше подходит инженерный подход к анализу данных? Содрать модели с Hugging Face и закинуть в прод — это тоже не всегда просто и тут уж точно вышмат тебе не сильно потребуется. Может, ты реально захочешь быть ML engineer’ом? А что если твоё — это быть Data Engineer’ом? Зачем тебе вообще тогда глубокие знания математики?!
Вижу часто острую проблему, что люди боятся начать работать в сфере, потому что им всё время кажется, что они ещё недостаточно знают. TODO-лист необходимых курсов у этих людей растёт быстрее, чем они успевают их проходить. Хватит собирать бесконечное образовательное комбо! Лучше начать практиковаться сейчас!
В случае если ты только на пороге входа в DS, то советую как можно раньше начать практиковаться в решении реальных кейсов. Уже по ходу дела навёрстывать необходимые математические знания. Будучи в реальных боевых условиях на зарплате хотя бы «джуна», ты быстрее раскачаешься, чем сперва 4 года отучишься, а уже потом придёшь работать тем же джуном, но с бОльшим запасом знаний.
Если тебе понравилась статья и ты хочешь узнать больше прикольных кейсов из моего опыта, то подписывайся на канал!
Так же, спасибо за ревью статьи Марку!

Комментарии (65)

eimrine
12.07.2022 12:34+4Недавно занимался одной задачей из области Data Science, остановился на том что есть у меня гауссиана (колоколообразная кривая нормального распределения) и мне надо как-то вычислить длинну отрезка AB, где A — экстремум, а B — произвольная точка на кривой. Какие инструменты мне нужно, как гуглить или где читать? Посыпаю голову пеплом за то что профилонил все 4 семестра вышмата.

marsermd
12.07.2022 13:00+3Пусть плотность вашего распределения -- F, m -- координата медианы (экстремума), x -- координата точки B.
Тогда расстояние по теореме Пифагора
sqrt((m - x) ^ 2 + (F(m) - F(x))^2)Или ты что-то другое имел в виду?

eimrine
12.07.2022 13:07+2Имел в виду отрезок который лежит на кривой, не просто прямая линия между A и B.

vassabi
12.07.2022 13:30+3у вас же компьютер есть! Надо что-то сложное посчитать - аппроксимируйте это : разбиваете промежуток от А до Б по оси х на промежутки - и в каждом считаете ф(х) (а потом простым пифагором - длину прямой между точками (х1,ф1) и (х2,ф2) ),
чем больше промежутков и чем они короче - тем точнее результат (дисклаймер - будьте внимательны со ступенчатыми данными и функциями с разрывами. Не бойтесь экспериментировать с количеством шагов :) )
А если хватает аналитического аппарата - то посчитайте интеграл.

Refridgerator
12.07.2022 14:38Аналитически не решается, только численно (например). Однако этот интеграл можно аппроксимировать рациональным многочленом в том же Вольфраме и пользоваться уже им. Если на входе экспериментальные данные, то их нужно сначала аппроксимировать гауссианной с учётом масштабирования и смещения относительно нуля.

AlanRow
12.07.2022 12:35+1На картинке под заголовком "Разогреваемся на простой математике" под знаком суммы, наверное, должна быть j, а не i. Сначала, думал, что это какой-то подвох, но не найдя нигде i предположил, что опечатка

Aleron75 Автор
12.07.2022 12:36+2Нет разницы как обозначать индекс. Не баг, а фича!

vesper-bot
12.07.2022 12:54+5Если под суммой индекс другой, чем в выражении, которое суммируется, можно получить неожиданный результат. Скажем, сумма по i от 2 до 4 от 2*j равна 6*j, а не какому-то конкретному числу. Это как с «d/dx монстром, который съел e^y», только в обратную сторону.

vesper-bot
12.07.2022 12:50Там под суммой j, только у неё хвост обрезан кривоватым кропом. Видно потому, что у j низ сильно ниже baseline'a.

vtal007
12.07.2022 13:09Так, а если от школы/вуза помню только про нормальные распределения, моды-медианы, квартили-процентили и еще в SPSS считали что надо (корреляции и факторный анализ), то все, путь в дата-саентисты закрыт? (и не надо учить питон)

Aleron75 Автор
12.07.2022 13:24Я лишь привел в пример, что сам частно в реальных боевых задачах использую.
Твой путь может быть иным) Начни со стажировок

vassabi
12.07.2022 13:40Раздел "Преобразование распределений" - напомнило про рисование красками "как из ярких разных цветов получить серобурый" :)

Tyusha
12.07.2022 14:16+31Когда говорят "высшая математика", то понятно, что это фигня на палочке на уровне первого курса. Никто, действительно знакомый с математикой, так еë никогда не назовëт.
И вот только в аспирантуре по терфизу начинаешь что-то подозревать о настоящем содержании давно знакомыми со школы слов "алгебра" и "математика", ибо понимаешь, что ты ещё только поскрëбла их по поверхности. 6 лет Физтеха недостаточно даже, чтобы понять всю глубину своего невежества. Чтобы хотя бы посмотреть в бездну, нужен Мехмат.
Савватеев как-то рассуждал о пяти этажах математики: что первый этаж это выпускник вуза, сам Савватеев (дфмн) оценивает себя на третьем этаже, а пятый этаж — это вообще космос, он не понимает даже, о чëм они вообще говорят, там обитают Уайлс и Перельман.

artemisia_borealis
12.07.2022 16:19+5Именно. Помню, что посмотрев алгебраическую квантовую теорию поля, что сквозь эти тернии не продерусь никогда…
А ведь помимо дебрей математики, есть ещё метаматематика, там тоже своя вселенная, книги Чёрча, Клини, Карри, Тарского, Фейса,…

sergeaunt
12.07.2022 19:25+5Когда говорят "высшая математика", то понятно, что это фигня на палочке на уровне первого курса. Никто, действительно знакомый с математикой, так еë никогда не назовëт.
Точно-точно. Так назовет человек, у которого был курс "Высшая математика", а других математических курсов не было.

Paul4850
13.07.2022 14:17Великий Арнольд уже много лет назад говорил о том, каким уровнем знаний должен обладать человек, называющий себя математиком. Весьма любопытно.
http://www.ega-math.narod.ru/Arnold.htm
Весьма сомневаюсь, что тот же Савватеев осилит этот "математический тривиум".

Refridgerator
13.07.2022 14:47Задачи интересные, но наблюдается выраженный перекос в сторону дифференциальных уравнений и полное отсутствие задач в стиле «описать математически то-то и то-то». Те же дифференциальные уравнения не из воздуха берутся при решении реальных прикладных задач. Вычислить 100-ю производную, построить графики — элементарно в любом мат.пакете, а вот вывести функцию для механизма Чебышева — уже нет.

Tyusha
14.07.2022 16:36Манифест Арнольда 1991 года, никаких матпакетов ещё. И он там сильно ещё переживает об актуальных на тот момент несправедливостях на Мехмате. (Сейчас наверное не всем понятно, поэтому поясню, что речь об антисемитизме)

Refridgerator
14.07.2022 21:42В 91-м я графики ещё на спектруме рисовал, а первая версия Mathematica их даже в текстовом виде выводить умудрялась. Но дело не в этом, а в том, что в задачах такого типа думать особо не надо — надо просто точно следовать определённому алгоритму для их решения, потому их и стало возможным автоматизировать. Намного сложнее задачи обратного характера — не рисовать график, а наоборот, вывести функцию, которая соответствует этому графику. Не считать предел в точке — а наоборот вывести функцию, предел в точке которой равен заданным значениям. Не раскладывать функцию в степенной ряд — а наоборот, по заданным коэффициентам определить производящую функцию.

dee3mon
12.07.2022 14:21+2Интересуюсь в качестве саморазвития. А в DataScience не используются операторные преобразования типа Фурье, разложения по вейвлетам, фильтрация с окнами и прочие элементы теории систем сигналов? В списке в явном виде не нашел.

N-Cube
12.07.2022 14:47+12Смотря где… Порой нужна и намного более сложная математика. Учитывая, что преобразование Фурье это основа спектрального анализа, то следующим уровнем идет анализ полиспектральный (и двойственный к нему кумулянтный), и вот там еще больше интересного — можно находить фрактальные свойства, в казалось бы, случайных распределениях и так далее. Вот, скажем, рельеф местности фрактален - и имеет почти 100% корреляцию с космоснимками или гравитационным полем, а вы попробуйте это численно показать (подсказка - нужно сначала выделить одинаковые полосы пространственных частот). Далее, рудоносность привязана к изменению значения фрактальности (подсказка - гидротермальные рудные потоки движутся по трещинам, подходящие системы трещин выделяются по значению фрактальности территории), и это проявляется в спектрах высшего порядка (если спектральный анализ оценивает соотношения между парами компонент, смещенных во времени или пространстве, что достаточно для поиска гауссовых процессов, то биспектральный анализ оперирует уже триплетами и этого достаточно для анализа фрактальности). Аналогично можно находить и удалять невидимые облака и их тени на космоснимках и еще много всего. В университете на кафедре с помощью полиспектрального анализа звуковых записей на морской микрофон даже подлодки в океане за сотни километров удавалось опознавать по уникальным паттернам двигателей (все двигатели периодичны, это видно на спектре, а вот тонкие различия видны на биспектре). Я на хабре несколько статей обо всем этом писал, в том числе, про совмещение всей этой математики с машинным обучением.

dee3mon
12.07.2022 20:25Но ведь названные у вас методы это ведь просто несколько более продвинутые виды анализа сигналов.. Там основным идеям и теориям порядка 50 лет, если не больше. Проблема была только в том, что закрытые аналитические решения находятся для считанных случаев. А для моделирования хоть сколько нибудь значимых ситуаций не хватало вычислительных мощностей.

N-Cube
12.07.2022 21:50+1Сейчас существуют методы решения и моделирования, которые хоть на программируемом калькуляторе можно реализовать для очень широкого класса задач - например, оценка сигналов непосредственно по их спектрам (и мультиспектрам), улучшение и восстановление изображений по их сверткам (тоже спектрам, только посчитанным и преобразованным в матричной форме), решение обратных задач путем линейного преобразования спектров... Если мы со спектрам считаем регрессии и корреляции, очевидно, здесь применимы и другие методы машинного обучения, скажем, анализ пространственных спектров рельефа с гауссовым ядром поможет выделить геологические структуры, анализ с асимметричными ядрами - определить направленность структур и так далее. Да даже корреляция уже не та, что была двадцать лет назад, когда только линейные связи надежно определялись, это ограничением осталось в прошлом - к примеру, distance correlation находит нелинейные зависимости в многомерных данных (разной размерности!), а вычисляется не сильно сложнее корреляции Пирсона (быструю многопоточную реализацию я писал сам, потому что такой библиотеки еще просто нет). Если вы точно понимаете, как соотносятся старые аналитические решения с новыми быстрыми матричными методами типа сверток в нейросетях (и как добиться сходимости и нужной точности) - то для вас за последние лет двадцать изменилось очень многое.

alex50555
13.07.2022 10:54+1Применяются. К примеру Фурье это сейчас мейнстрим в обработке аудио. Переводят временной ряд с помощью Фурье в картинку-спектрограмму, потом ещё парочка преобразований, а потом свертками по ней проходятся.
Вот небольшая статья на русском:
https://vc.ru/newtechaudit/358176-sposoby-predstavleniya-audio-v-ml

Dark_Hobbit
15.07.2022 09:50Из того что знаю - ряды Фурье используются для прогнозирования временных рядов. Например, достаточно популярная библиотека FbProphet использует именно этот подход.

red_elk
12.07.2022 15:19+2В вопросе про медиану первая мысль была что красный столбец - это мода. Но медиану проще конечно посчитать.

0xd34df00d
12.07.2022 16:56+2Зачем какой-то бутстрап для того, чтобы сделать нормальное распределение из равномерного? Достаточно просто взять обратную функцию распределения: легко видеть (даже мне с отсутствующей интуицией теорвера), что если x = F-1(U), то x ~ F. И так можно получать не только нормальные распределения.

Aleron75 Автор
12.07.2022 17:41+1Интересно, откуда ты возьмешь функцию распределения на основе данных?
Можно апроксимировать распределение, но это тоже не всегда легко.
Будстап проще всего.
akhalat
12.07.2022 17:44+2Интересно, откуда ты возьмешь функцию распределения на основе данных?
А ещё интересней, что в вопросе явно сказано «математически» и явно дано равномерное распределение на отрезке.

akhalat
12.07.2022 17:42+2Зачем какой-то бутстрап для того,
Стильно, модно, молодежно…
В последние время уже не первый раз встречаю, как этот «бутстреп» пытаются везде запихнуть, без понимания где он нужен и не нужен. Видать очередной тренд.

nikolay_karelin
12.07.2022 19:10+4Из высшей математики больше всего нужны теория вероятности и математическая статистика. И конечно линейная алгебра. Мат анализ - в гораздо-гораздо меньшей степени.

Refridgerator
12.07.2022 19:50+1Ну вот тут человек выше захотел посчитать длину дуги гауссианы — и не смог. Ни теория вероятностей, ни математическая статистика, ни линейная алгебра в этом не помогут.

sci_nov
12.07.2022 22:04+1интересно, зачем это ему понадобилось? Ладно бы площадь под кривой... Длина даже в теории не используется, а на практике - большой вопрос...

N-Cube
13.07.2022 12:31Длина кривой по известному уравнению непрерывной кривой вычисляется элементарно через первую производную и определенный интеграл, это и есть матанализ. Вполне очевидно - считаем приращения (дифференциал) на единицу координаты и интегрируем по всему интервалу. Хотите тервер и матстатистику вместо матанализа - пожалуйста, и так можно, посчитайте случайные попадания случайной величины известного распределения в узких столбцах ниже и выше кривой и тоже получите ее длину. Линейная алгебра тоже даст ответ - используем конформное отображение гауссианы в круг, а длину окружности мы знаем. А если с помощью конформного отображения гауссианы построите оптимальное распределение случайной величины для оценки длины кривой методом Монте-Карло - то еще и считаться будет быстро с заданной точностью.

Red_Nose
12.07.2022 23:38+1Так тонко, как автор (почти), шутить не умею, но попробую :)
" Ребята с «вышкой» всё время умничают, что в Data Science нужна «математика», но стоит копнуть глубже, оказывается, что это не математика, а вышмат. " - ага, т.е. знания таблички умножений таки недостаточно :( Ладно будем осиливать дискриминант. Потом интригалы и вот эти всякие алгебры, кольца, группы, цепи, ... на начальном этапе. А потом (лет через 5-10) даже начинаешь понимать зачем это "фсьо" надо. Так и до чтения Бурбаки в качестве научпопа дойти можно :)
0xd34df00d
13.07.2022 00:33+5Там уже, правда, интерес к датасайенсу отваливается.

justPersonage
13.07.2022 10:01А к чему он появляется?

0xd34df00d
13.07.2022 17:20К тому, что поближе к этим всем Бурбаки.

Refridgerator
14.07.2022 09:20Известная шутка: ученик Бурбаки на вопрос «сколько будет 2+3» ответил: «3+2, так как сложение коммутативно».

DabjeilQutwyngo
13.07.2022 08:38А как вы отличаете ситуацию, когда действительно верно описали зависимость, от той, когда она вам показалась? Каким методом устанавливаете однородность эмпирических распределений, и требуется ли такое вообще в DS и зачем?

FedorDS
13.07.2022 15:41По-идее, качества на валидационной и тестовой выборках достаточно, если правильно понял вопрос

DabjeilQutwyngo
14.07.2022 02:43В целом, первый вопрос поняли в той степени, в которой сталкивались с этой проблемой, видимо. Он минимум с двумя подводными камнями: (а) зачем при нынешних вычислительных мощностях вообще описывать зависимость (распределение величин), (б) характер и объём данных может не позволять применить валидационную и тестовую выборки, например, когда каждый экземпляр единственен и уникален (например, химическое соединение, идентифицируемое формулой). А на второй вопрос ничего не написали, хотя он ещё более интересен.

FedorDS
13.07.2022 10:54Иногда, когда читаешь какие-то новые статьи с новыми моделями и новыми подходами - требуется хорошее понимание математики для того, чтобы разобраться, как это работает и как у себя можно такое заимплементить (думаю, что навык уметь воспроизводить статьи не считается чем-то совсем уже заоблачным и у джунов можно его просить). Если же статье 100000 лет - можно легко найти реализацию и не заморачиваться, поэтому, вопрос в том, насколько вы на острие науки.
PS, я не упомянул рисерчеров, которые эти новые подходы разрабатывают, потому что статья про то, что нужно для условного "джуна"

Daddy_Cool
13.07.2022 12:25На первом графике в формуле где A, B, C... зачем у вас точки? У вас нет скалярного произведения, вы не перемножаете числа, вы не пишете программу в Маткаде.

punhin
14.07.2022 16:13Эксперт - это тот, кто может точно и правдоподобно объяснить, почему не сбылся его прогноз. К сожалению, в наше время знания предметной области, общих и частных разделов математики не являются ни достаточным, ни даже необходимым условием для того, чтобы быть экспертом.



datacompboy
А если я умею вот так это засчитывается?
Aleron75 Автор
Да, сойдет. Заходи за зарплатой
Andy_U
А, кстати, где там плюс/минус у корня от n? Впрочем, и у автора нет.
Refridgerator
Так n там всегда положителен (для действительных аргументов).
Andy_U
Если n=x^2, то x=(+/-)sqrt(n). Т.е. правая часть (без квадрата) равно плюс/минус корень из n
Refridgerator
Wolfram Alpha и выдал два решения для Z.
Andy_U
А, теперь увидел. Я как-то больше к Maple привык. Значит, это претензия только к автору статьи. Thx.
Refridgerator
Решений может быть больше, чем два, поэтому Wolfram выдаёт их списком. Если решений бесконечно, Wolfram добавляет дополнительный (или дополнительные) целочисленный аргумент к функции.