Практически 10 лет и 50 статей назад, я набросал материал о моём знакомстве с замечательной системой компьютерной алгебры Maxima. Время шло, ничто не предвещало беды, но неожиданно я осознал, что дети имеют свойство взрослеть и скоро я не смогу решать школьные задачки в уме.

Пришло время сдуть пыль с "комплюхтера", установить себе Maxima и попутно еще раз напомнить сообществу о ней.

Сегодня не будем всё усложнять. Мы рассмотрим простейшие примеры для 6 и 7 классов по следующим темам:

• наименьшее общее кратное:

• наибольший общий делитель;

• операции с дробями;

• упрощение выражений с одночленами и многочленами;

• линейные уравнение;

• системы линейных уравнений;

• построение графиков функции;

Оглавление

• Немного о Maxima

• 6-й класс (НОД, НОК, дроби)

• 7-й класс (многочлены, уравнения, графики)

• Заключение

Немного о Maxima

Начать стоит как обычно с дисклеймера. Я не гуру в области компьютерной алгебры в целом и Maxima в частности, просто в счастливую институтскую пору ковырял её из любопытства, в надежде компенсировать свои слабые стороны в математике. Поэтому, всё в этой статье не является истинной в последней инстанции.

Maxima это система компьютерной алгебры с открытым исходным кодом, которая более-менее активно развивается. Максима позволяет решать задачи так как будто вы на уроке математики. Например, когда я пытался пройти курс по машинному обучению и застрял на том, что не могу найти частную производную, эта распрекрасная чудо-программа меня сильно выручила.

Maxima имеет аналоги, но мы сегодня не будем обсуждать, что лучше, а что хуже.

Лучше перейдем к установке приложения.

У Maxima есть сборки, под Windows, Linux, MacOS и даже под Android (но она с 2018 года не развивается). Скачать можно по ссылке. Если не хотите устанавливать, можно использовать одну из Web версий. В данной статье я использовал Maxima 5.46.0.

Вообще Maxima это консольное приложение:

Но я дальше буду использовать графическую надстройку WxMaxima, которая идет в комплекте с пакетом для Windows.

6-й класс (НОД, НОК, дроби)

Начнем с простейших задач и в процессе познакомимся с системой.

Если вы знакомы с современными языками программирования, скорее всего освоить азы Maxima вам не составит труда, вводим команды и аргументы, можно даже создавать свои функции и переменные.
А если вы стильный, модный, молодежный аналитик данных и видели, как выглядит Jupyter блокнот, то заметите "неуловимое" сходство.

В Maxima есть поля разного типа, которые, по сути можно поделить на вычисляемые и информационные (текстовые).

Еще одно важное примечание, чтобы не путать программные функции и математические, в данной статье я буду функции Maxima называть командами.

Давайте без промедлений найдем наименьшее общее кратное двух чисел с помощью команды lcm(). Если вдруг вы забыли, то наименьшее общее кратное это число которое поделиться без остатка на все числа, что мы укажем в аргументах функции lcm().

Как видите можно вводить больше двух аргументов.

lcm(12,15);
lcm(8,12);
lcm(6,12,18);

Чтобы побаловаться самостоятельно вставьте этот код в окно редактора и нажмите "зеленую стрелку" или shift+enter

Перейдем к наибольшему общему делителю. Напомню, что для двух чисел это наибольшее натуральное целое число, на которое эти числа делятся без остатка.

В Maxima для нахождения НОД мы используем команду gcd()

gcd(15,25);

К сожалению, использовать три аргумента в этой команде нельзя.

Действия с дробями.

С дробями можно проводить все привычные арифметические действия, а еще можно переводить десятичные дроби в обыкновенные командой rat().

При работе с дробями есть один недостаток если вы хотите написать смешанную дробь например:

То придется слегка "поплясать с бубном" (в интернете есть советы).

Код из примера:

1/2*3;
(5/7)+(11/12)-(9/14);
%;
%o67;
rat(0.25);

Обратите внимание в Maxima можно ссылаться на предыдущие результаты ввода данных и вывода.

Если просто вставить "%" вернется последний ответ.
А если написать "%o67" то вернется ответ конкретно из ячейки 67, даже если его не видно на экране (при условии что он был ранее рассчитан)

7-й класс (многочлены, уравнения, графики)

Чтобы не раздувать статью, дальше пойдём чуть быстрее.

Начнем с упрощения выражений.

Давайте в этот раз разберем каждый блок отдельно

(5*x^2+x)/x;

Я специально описал выражение отдельно, чтобы вы смогли посмотреть, как Maxima создает символьную форму записи для выражения.

rat(%);

команда rat() упрощает рациональные выражение (дроби). В данном случае мы подставляем в неё предшествующий ответ.

factor(2x^2+2x);

Вынесет нам общий множитель за скобки.

выраж:a^2+2ab+b^2;

factor(выраж);

В Maxima можно задать переменные с помощью записи имя_переменной:значение
Как видите можно использовать и русскоязычные переменные (хотя наверное все же не желательно).

ab:(a+b)*(a+b);

Создадим англоязычную переменную

И раскроем скобки командой expand(ab)

Кстати, можно получить справку о команде не выходя из Maxima, с помощью describe(команда).

Давайте перейдем к уравнениям.

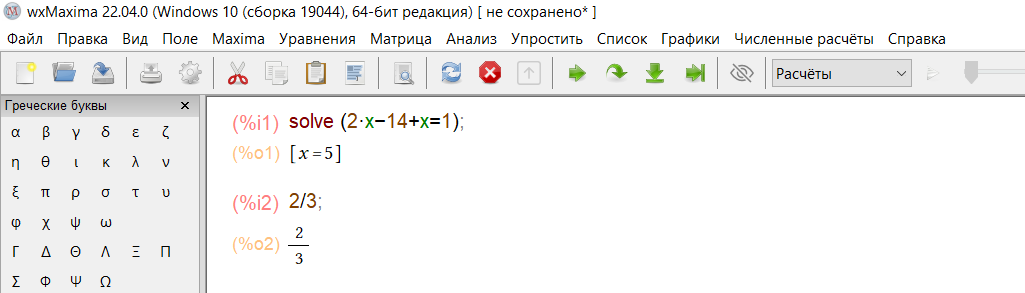
Уравнения и системы уравнений решает волшебная команда solve().

solve(2*x+2=11+x);

Решит наше простое уравнение.

eq1:x+2*y=9;
eq2:y=x+3;
solve([eq1,eq2]);

А вот тут уже интересней. В переменные мы задаем два уравнения, а потом передаем их в команду solve в качестве массива (в квадратных скобках через запятую).

Мы можем проверить решение уравнения, подставив в уравнение полученные значения.

ev([eq1,eq2],[%]);

В этом случае мы вставляем верный ответ.

ev([eq1,eq2],[y=3,x=2]);

А в этом взятые "с потолка" значения. Как видим правая и левая половины уравнения не сходятся.

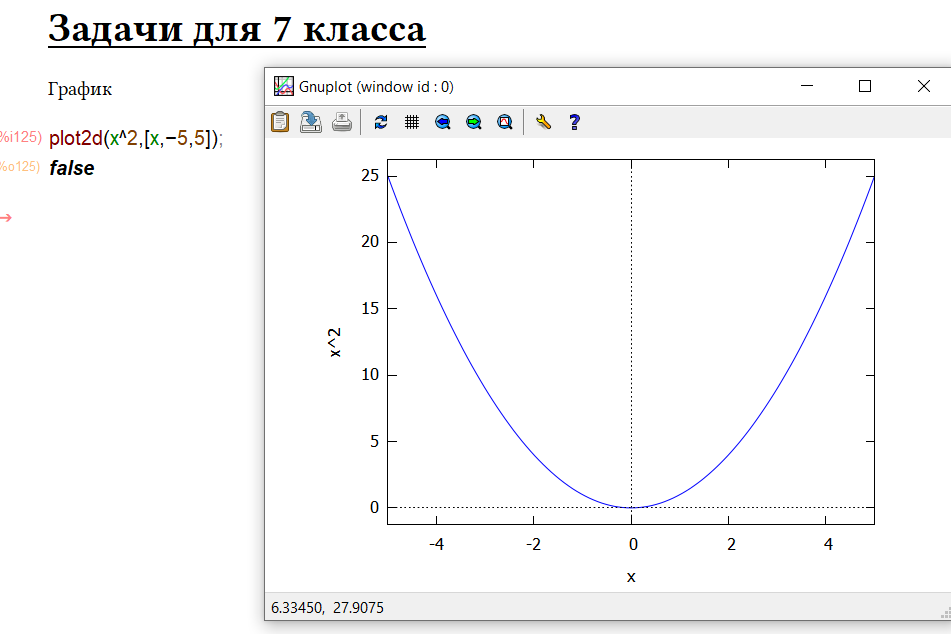
Ну и последнее, чисто для затравки это графики, я не буду разбирать подробно, оставлю на другой раз ибо много нюансов.
Просто продемонстрирую, что Maxima умеет рисовать графики (в данном случае двухмерный):

Заключение

На самом деле множество задач, что я показал в статье можно решить с помощью кучи альтернативных инструментов, Интернет просто пестрит сервисами как найти НОД и НОК онлайн, есть инструменты для построения графиков, есть SymPy для Python и так далее.
Но мне кажется, что знать о существовании Maxima полезно и взрослым, и школьникам.

Для решения базовых задач этот простой инструмент не требует навыков программирования, но при этом в будущем может стать первым шагом к освоению языков программирования и пониманию их изначальной связи с математикой.

Спасибо всем, кто дочитал до конца!

P.S. Если я пойму, что статья вам понравилась, то продолжу цикл для старших классов.