Данная статья в большей мере является уточнением моей предыдущей статьи по оптимизации перебора на шахматной доске с ферзями.
https://habr.com/ru/post/679200/
Оптимизация перебора в данной задаче, это не только лишь хардкорное скоростное решение на базе 64-битной арифметики и SIMD-стиля. Это внесение в алгоритм решений, позволяющее сократить само количество шагов перебора. Пока я представляю начальный позиционный анализ.
Уточнением к моей предыдущей статье, является то что я добавил позиционный анализ не только к столбцам, но и к строкам. Пришлось довольно долго помучится для наиболее эффектной реализации. Задача крылась в решении, как быстро просуммировать атаки в строке шахматной доски, если я базовое движение совершаю по столбцам. Перепробовав несколько вариантов с битовыми играми, я остановился на том чтобы во время маркировки атак, вести альтернативную шахматную доску повернутую так, что X и Y просто меняются местами (инверсия осей). Для этого потребовалось ввести только три дополнительные переменные.
Некоторые коллеги читавшие мою статью, видимо не уловили смысл происходящего и пытаются утверждать, что всё равно совершается полный перебор позиций на доске. Но это совершенно не так.
Оптимизирующий алгоритм выглядит сейчас так:
Перед установкой нового ферзя:
Проверить, что на доске стоит полный комплект ферзей. Если да, то рапортовать об успехе. Снять последнего установленного ферзя, шаг назад.
Определить есть ли такой столбец на ВСЕЙ доске, в котором нет ферзя, но все клетки этого столбца являются атакованными. Если такой столбец имеется, то прервать перебор, шаг назад
Определить есть ли такая строка на ВСЕЙ доске, в которой нет ферзя, но все клетки этой стоки являются атакованными. Если такая строка имеется, то прервать перебор, шаг назад.
Определить есть ли такой столбец на ВСЕЙ доске, в котором нет ферзя, но можно поставить только одного ферзя. Если такой столбец имеется, то поставить туда ферзя, перейти к пункту №1.
Определить есть ли такая строка на ВСЕЙ доске, в которой нет ферзя, но можно поставить только одного ферзя. Если такая строка имеется, то поставить туда ферзя, перейти к пункту №1.
Берем свободный столбец ближе к началу, определяем свободные места в нем, начинаем перебором ставить туда ферзей. Поставив очередного ферзя идем к пункту №1.
Для понимания практичности этого анализа приведу иллюстрации:

По классике базовое движение по столбцам A-H, выставляем перебором ферзей по строкам №1-8. Имеем трёх установленных ферзей A1,B3,C5. "Как бы" собираемся прогуляться перебором по столбцу D в котором осталось три свободные клетки: D2,D7 и D8.
Но тут "Как бы" выключается и включается мой механизм оптимизации перебора...
Когда приступаем к установке 4-го ферзя, обнаруживаем, что на доске образовался такой столбец, что в него можно поставить только одного ферзя. Это позиция F4. Эта позиция отстоит вперёд на два столбца, то есть не является следующей-очередной. Установка туда ферзя уже не засчитывается, как перебор, так как "очередной" столбец D имеет три свободные клетки. Внеочередную установку ферзя в F4 я называю - реверсом.

Установкой ферзя F4 - замечательным образом мы заодно выбьем клетку D2 с которой бы начался классический перебор на 4-го ферзя. Но тут уже видно, что следующим кандидатом на ферзя будет клетка H7, поскольку она осталась единственной в колонке H.

Проставив H7 мы атакуем клетку G6. И в следствии атаки на G6 возникает ситуация, что строка №6 не имеет ферзя, но все клетки строки №6 являются атакованными. В данном случае после установки пятого ферзя, выясняется, что данная комбинация не имеет продолжения, два ферзя F4 и H7 снимаются с доски, ферзь с C5 перемещается на C6.
На доске после 5-го ферзя остались "не перебранными" клетки: D8, E2, E8, G2
Как бы сказал шахматист, - поставив ферзей на A1+B3+C5 - мы получаем образно выражаясь - "мат в два хода".
Классические алгоритмы по расстановке ферзей обычно движутся строго линейно, и циклично осуществляют маркировки атак "вперед". В моём алгоритме все маркировки атак заготовлены заранее и предусматривают маркировку атак "назад".
Хардкорные битово-арифметические операции мне позволяют достаточно быстро производить анализ текущих атак. Новый листинг алгоритма прилагается.
using System;
//using System.Numerics.BitOperations;
using System.Runtime.InteropServices;
namespace Queen_8x8
{
delegate void Solution(int[] queens);
class Program
{
static Queen_8x8 task = new Queen_8x8();
static void Main(string[] args)
{
print("Hello Queens!");
print(":");
task.init(print_solution);
//task.init(null);
task.run();
print(":");
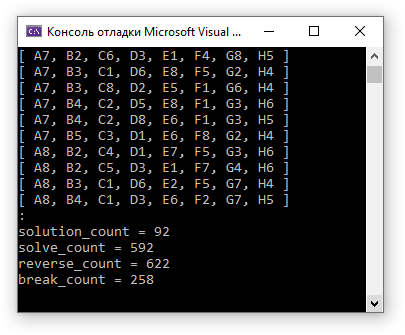
print("solution_count = " + task.solution_count);
print("solve_count = " + task.solve_count);
print("reverse_count = " + task.reverse_count);
print("break_count = " + task.break_count);
}
static void print(String s)
{
Console.WriteLine(s);
}
static void print_solution(int[] queens)
{
String s = "";
s += "[ ";
for (int i = 0; i < queens.Length; i++)
{
s += Char.ConvertFromUtf32(i + 65) + (queens[i] + 1).ToString();
if (i < (queens.Length - 1)) s += ", ";
}
s += " ]";
print(s);
}
}
class Queen_8x8
{
protected Solution solution = null;
public const int total_queens_count = 8;
public const int diag_count = total_queens_count * 2 - 1;
//public ulong markers = 0xFFFF_FFFF_FFFF_FFFF;
public int[] queens = new int[total_queens_count];
int current_queens_count = 0;
ulong[] diag_LR = new ulong[diag_count];
ulong[] diag_RL = new ulong[diag_count];
public ulong attacks_VT = 0; // атака по вертикали
public ulong attacks_VZ = 0;
public ulong attacks_HZ = 0; // атака по горизонтали
public ulong attacks_HT = 0;
public ulong attacks_LR = 0; // атака по диагонали BL-TR [\]
public ulong attacks_RL = 0; // атака по диагонали BR-TL [/]
// Инверсные атаки по диагоналям. X и Y меняются местами
// Введедены для последующего быстрого суммирования атак по строкам
public ulong attacks_LRZ = 0;
public ulong attacks_RLZ = 0;
// Statisticks
public int solution_count = 0;
public int solve_count = 0;
public int reverse_count = 0;
public int break_count = 0;
static void print(String s)
{
Console.WriteLine(s);
}
private int get_LR(int x, int y) { return x + y; }
private int get_RL(int x, int y) { return (total_queens_count - 1 - x) + y; }
private void reset()
{
solution_count = 0;
solve_count = 0;
reverse_count = 0;
break_count = 0;
current_queens_count = 0;
attacks_VT = 0;
attacks_HT = 0;
attacks_HZ = 0;
attacks_VZ = 0;
attacks_LR = 0;
attacks_RL = 0;
attacks_LRZ = 0;
attacks_RLZ = 0;
for (int i = 0; i < queens.Length; i++)
{
queens[i] = -1;
}
}
public void run()
{
reset();
solve();
}
public void init(Solution solution)
{
this.solution = solution;
for (int i = 0; i < diag_count; i++)
{
diag_LR[i] = 0;
diag_RL[i] = 0;
}
for (int x = 0; x < total_queens_count; x++)
{
for (int y = 0; y < total_queens_count; y++)
{
ulong mask = 1UL << ((x << 3) + y);
diag_LR[get_LR(x, y)] |= mask;
diag_RL[get_RL(x, y)] |= mask;
}
}
}
protected void step(int qx, int qy)
{
ulong a_VT = 0xFFUL << (qx << 3);
ulong a_HT = 0xFFUL << (qy << 3);
ulong a_VZ = 0x0101_0101_0101_0101UL << qx;
ulong a_HZ = 0x0101_0101_0101_0101UL << qy;
ulong a_LR = diag_LR[get_LR(qx, qy)];
ulong a_RL = diag_RL[get_RL(qx, qy)];
ulong a_LRZ = diag_LR[get_LR(qy, qx)];
ulong a_RLZ = diag_RL[get_RL(qy, qx)];
// Set Queeen
++current_queens_count;
queens[qx] = qy;
attacks_VT |= a_VT;
attacks_HT |= a_HT;
attacks_HZ |= a_HZ;
attacks_VZ |= a_VZ;
attacks_LR |= a_LR;
attacks_RL |= a_RL;
attacks_LRZ |= a_LRZ;
attacks_RLZ |= a_RLZ;
// Recurse
solve();
// Remove Queeen
attacks_VT &= ~a_VT;
attacks_HT &= ~a_HT;
attacks_HZ &= ~a_HZ;
attacks_VZ &= ~a_VZ;
attacks_LR &= ~a_LR;
attacks_RL &= ~a_RL;
attacks_LRZ &= ~a_LRZ;
attacks_RLZ &= ~a_RLZ;
queens[qx] = -1;
--current_queens_count;
}
protected void solve()
{
if (current_queens_count == total_queens_count)
{
++solution_count;
solution?.Invoke(queens);
return;
}
// Проверка по столбцам
ulong attacks_v = attacks_HZ | attacks_VT | attacks_LR | attacks_RL;
// Получаем в каждом байте 64-разрядного числа -
// сумму занятых мест по столбцам
// Каждый байт обозначает столбец таблицы и содержит число
// атак в интервале от 0 до 8
ulong sum_vec_8_columns = BitOp.popcnt64_bv(attacks_v);
// Проверка, что остались незаполненные столбцы
// Определяем что в каком либо столбце присуствует число 8
// Если в каком-либо столбце присутствует число 8,
// то общее значение теста станет ненулевым
ulong test = sum_vec_8_columns & 0x0808_0808_0808_0808UL; // Маскируем байты для обнаружения числа 8
test &= ~attacks_VT; // Отбрасывем столбцы (columns), где уже установлены ферзи
if (test != 0)
{
++break_count;
return; // Нашёлся столбец, куда невозможно установить ферзя
}
// Проверка по строкам
ulong attacks_h = attacks_HT | attacks_VZ | attacks_LRZ | attacks_RLZ;
// Получаем в каждом байте 64-разрядного числа -
// сумму занятых мест по строкам
// Каждый байт обозначает строку таблицы и содержит число
// атак в интервале от 0 до 8
ulong sum_vec_8_rows = BitOp.popcnt64_bv(attacks_h);
test = sum_vec_8_rows & 0x0808_0808_0808_0808UL; // Маскируем байты для обнаружения числа 8
test &= ~attacks_HT; // Отбрасывем строки (rows), где уже установлены ферзи
if (test != 0)
{
++break_count;
return; // Нашлась строка, куда невозможно установить ферзя
}
int qx, qy;
ulong column, row;
// Проверка, на то что есть столбцы, только с одим возможным ходом
// Поскольку мы отбросили вариант, что в столбцах присутствует число 8
// прибавляем к каждому столбцу единицу и опять проверяем все столбцы
// на наличие числа 8
// Если изначально в каком-либо столбце присутствовало число 7,
// то общее значение теста станет ненулевым
test = sum_vec_8_columns + 0x0101_0101_0101_0101UL;
test &= 0x0808_0808_0808_0808UL & ~attacks_VT;
if (test != 0)
{
++reverse_count;
qx = BitOp.bsr64((test >> 3)) >> 3;
column = (~attacks_v >> (qx << 3)) & 0xFFUL;
qy = BitOp.bsr64(column);
step(qx, qy);
return;
}
// Аналогичным образом, проверяем, что есть такая строка в которую можно
// поставить только одного ферзя
test = sum_vec_8_rows + 0x0101_0101_0101_0101UL;
test &= 0x0808_0808_0808_0808UL & ~attacks_HT;
if (test != 0)
{
++reverse_count;
qy = BitOp.bsr64((test >> 3)) >> 3;
row = (~attacks_h >> (qy << 3)) & 0xFFUL;
qx = BitOp.bsr64(row);
step(qx, qy);
return;
}
// Делаем перебор по столбцу
test = sum_vec_8_columns + 0x0202_0202_0202_0202UL;
test &= 0x0808_0808_0808_0808UL & ~attacks_VT;
if (test != 0)
{
qx = BitOp.bsr64((test >> 3)) >> 3;
}
else
{
qx = BitOp.bsr64(~attacks_VT) >> 3;
}
//--
column = (~attacks_v >> (qx << 3)) & 0xFFUL;
while (column != 0)
{
++solve_count;
qy = BitOp.bsr64(column);
column &= ~(1UL << qy);
step(qx, qy);
}
return;
}
}
class BitOp
{
// Просумировать все биты в байтах 64-разрядного числа
public static ulong popcnt64_bv(ulong value)
{
ulong result = value;
result = result - ((result >> 1) & 0x5555_5555_5555_5555UL); // Результат сумм по 2-а бита
result = (result & 0x3333_3333_3333_3333UL) + ((result >> 2) & 0x3333_3333_3333_3333UL); // Результат сумм по 4-е бита
result = (result + (result >> 4)) & 0x0F0F_0F0F_0F0F_0F0F; // Результат сумм по 8-ь бит
return result;
}
public static byte add64_bv(ulong value)
{
ulong result = value;
result += result >> 8; // Результат сумм по 16-ь бит
result += result >> 16; // Результат сумм по 32-ь бит
result += result >> 32; // Результат
return (byte)(result);
}
/*
* Подсчитать кол-во битов установленных в 1 в 64-разрядном числе
* Полностью эквивалентна машинной инструкции Intel x86/x64 - POPCNT
*/
public static byte popcnt64(ulong value)
{
ulong result = value;
result = result - ((result >> 1) & 0x5555_5555_5555_5555UL); // Результат сумм по 2-а бита
result = (result & 0x3333_3333_3333_3333UL) + ((result >> 2) & 0x3333_3333_3333_3333UL); // Результат сумм по 4-е бита
result = (result + (result >> 4)) & 0x0F0F_0F0F_0F0F_0F0F; // Результат сумм по 8-ь бит
result += result >> 8; // Результат сумм по 16-ь бит
result += result >> 16; // Результат сумм по 32-ь бит
result += result >> 32; // Результат
return (byte)(result);
}
public static byte popcnt8(byte value)
{
ulong result = value;
result = result - ((result >> 1) & 0x55); // Результат сумм по 2-а бита
result = (result & 0x33) + ((result >> 2) & 0x33); // Результат сумм по 4-е бита
result = (result + (result >> 4)) & 0x0F; // Результат сумм по 8-ь бит
return (byte)(result);
}
public static int bsr64(ulong value)
{
if (value == 0) return -1;
int bitpos = 0;
ulong mask = 0xFFFF_FFFF_FFFF_FFFFUL;
int step = 64;
while ((step >>= 1) > 0) // 6-итерационный проход
{
if ((value & (mask >>= step)) == 0)
{
value >>= step;
bitpos |= step;
}
}
return bitpos;
}
}
}
2056 ./ 592 = 3,5 - Сокращение вариантов перебора.
2056 - как говорилось в предыдущей статье, количество. шагов перебора без моего позиционного анализа.
Если двигать первого ферзя только по клеткам A1-A4, кол-во переборов уменьшается вдвое
592 / 2 = 296
Я предварительно для статьи пытаюсь убрать из алгоритма всё обрамление и мои исследования, чтобы осталась только чистая логика оптимизации.
P.S. Продолжение возможно последует...


alxndrlsn
Спасибо за труд! Любопытно даже стало, когда человек интуитивно расставляет ферзей не этим ли путем идет или использует какой-то более эффектный метод пространственной оптимизации?
п.с. человек все-таки воспринимает как минимум в 3D-пространстве, а это уже математика более высокого ранга...
nuzha Автор
Затрудняюсь тут ответить про 3D. Следующим уровенем оптимизации перебора - будут паттерны. Я пытался знакомых озадачить, по каким критериям первая картинка в статье не имеет дальнейшего решения, не рассматривая вариантов дальнейшего перебора. Пока мне никто не смог дать логичного ответа. А он - есть. Постановка ферзей на A1+B3+C5 не имеет дальнейшего решения, в этой комбинации уже имеется стоп-сигнал.
Это означает - что, смотрят, но не видят. Интуиция видимо срабатыаает, только тогда, когда мозг хорошо натренирован.