Казалось бы, что можно добавить на тему о популярной задачке о расстановке ферзей на шахматной доске стандартной размерности 8x8 клеток? Но как оказалось и тут можно внести свою толику программистской мысли.
Классически задача решается последовательным перебором ферзей на заданной линии и бонусом предлагается анализировать диагонали которые покрываются установкой ферзя в нужную клетку. Но те реализации алгоритмов, что я видел, установкой или снятием ферзя с маркировкой диагоналей, едва ли перекрывают по быстродействию расстановку ферзей по-принципу ладьи.
Как оказывается в алгоритм можно привнести существенные улучшения отказавшись от линейного обхода/перебора клеток и внеся понятие анализа состояния атак шахматной доски.
Я добавил два улучшающих принципа в алгоритм, которые позволяют снизить общее кол-во переборов в три раза.
Двигаемся по столбцам (A-H). В столбцах перебираем строки (1-8)
Установить ферзя, означает - промаркировать все атаки (горизонтальную и диагональные) и пометить столбец с ферзём, как занятый.
Снять ферзя, означает снять маркировку атак и пометить столбец, который он занимал, как свободный.
Проверить поставлены ли все ферзи во всех столбцах. Если да, то выдать удачный результат.
Вернуться на шаг назад в переборе (снять последнего установленного ферзя).
Рекурсивно переходим к пункту №1.Проверить, есть ли такой свободный столбец, в который нельзя поставить ферзя?. Если такой столбец имеется - шаг назад в рекурсивном обходе, дальнейшие ходы - бессмысленны.
Вернуться на шаг назад в переборе (снять последнего установленного ферзя).
Рекурсивно переходим к пункту №1.Проверить, есть ли такой свободный столбец в который можно поставить только одного ферзя? Если такой такой имеется, разумеется туда и ставим ферзя, жертвуя линейностью обхода. Рекурсивно переходим к пункту №1.
Находим ближайший к началу доски свободный столбец, выполняем в нем перебор всех не атакованных позиций. Устанавливаем ферзя в не атакованную позицию.
Рекурсивно переходим к пункту №1
Для реализации алгоритма я выбрал 64-х битную математику в арифметических и логических операциях. [ + - AND NOT XOR OR << >>].
Шахматная доска 8x8 в 64 клетки отлично ложится в 64-х битовую переменную.
Чтобы не использовать внутренние циклы для маркировки состояний по диагонали, я инициализирую их заранее. Есть три раздельных слоя для маркировки атак ферзя. Два диагональных слоя и один горизонтальный. В один слой все три атаки сливать нельзя, так как это не позволит восстановить предыдущее состояние шахматной доски.
Для демонстрации своего алгоритма я выбрал язык C#, как наиболее легкий и понятный. JS не содержит поддержки целочисленной 64-х битной арифметики, и чтобы не усугублять демо-пример кластеризацией на 32-х битную арифметику - я от него отказался.
Язык СИ несколько тяжелей, по тексту, но содержит поддержку нужных для ускорения работы алгоритма инструкций процессора - POPCNT и BSR в виде "intrinsics"-функций.
С JVM на момент написания этой статьи существуют некоторые неопределённости, о которых не будем распространяться.
В итоге выбран C# с дополнительным классом битовой логики, который пытливый программист сам может переложить на процессорную аппаратную поддержку.
Итак приступим!
Размещаем шахматную доску в 64-битную переменную следующим образом

Первого ферзя в алгоритме ставим на [A1] (x = 0, y = 0). Базовое движение делаем по X-оси (по столбцам), на каждой оси перебираем позицию Y (строки). Как видно из иллюстрации, каждый столбец представляет из себя байт (8-мь бит).
Теперь промаркируем диагонали:

Номер LR-диагонали считается по формуле: N = X+Y
Так например, для позиций (xy): 3:2 (26), 4:1 (33), 1:4 (12) - Номером диагонали будет - 5;
для позиций (xy): 7:4 (60), 5:6 (46), 4:7 (39) - Номером диагонали будет - 11;
Диагональ LR: (LEFT+BOTTOM : RIGHT+TOP)

Номер RL-диагонали считается по формуле: N = 7 - X+Y
Ну а дальше - дело техники:
Вводим массивы:
ulong diag_LR[15]
ulong diag_RL[15]
Массивы содержат шахматную доску где биты установленные в 1 означают атаку по диагонали. Предварительно инициализируем их. Данные массивы нужны для того, чтобы не вводить в основной цикл внутренние циклы для маркировки атак. Массив для горизонтальной атаки не нужен, поскольку легко накладывается 64-битным числомВводим переменную "ulong markers". Каждый байт markers содержит либо 0x00, либо 0xFF, чтобы обозначать доступен ли X-столбец для установки ферзя.
0xFF - доступен
0x00 - занятВводим три переменные (ulong): attacks_HZ, attacks_LR, attacks_RL, чтобы держать состояния атак по горизонтали и вертикалям. Чтобы получить полное состояние всех атак клетки, надо слить их по операции OR: attacks_HZ | attacks_LR | attacks_RL.
Для понимания работы алгоритма надо также понимать, что часть операций над 64-х разрядными числами можно совершать параллельно над байтами числа, если числа хранимые в байтах не вызывают арифметического переполнения относительно друг-друга. Например число 0x0303_0303_0303_0303 - можно рассматривать, как вектор из 8-ми байтов установленных в 3-и. Тогда операцией инкрементации вектора будет прибавление к числу - значения 0x0101_0101_0101_0101. Результатом будет - 0x0404_0404_0404_0404.
Ответом на вопрос - "В байт векторе присутствуют байты со значениями в диапазоне от 0 до 8. Есть ли в байт-векторе, хотя бы одно число 8?" - будет наложение на вектор маски - 0x0808_0808_0808_0808 операцией AND. Ненулевое значение означает, что байт-векторе есть такие числа.
0x0108_0304_0708_0506
AND
0x0808_0808_0808_0808 =
-----------------------------------
0x0800_0000_0008_0000 - ЕСТЬ (ненулевой результат)
0x0106_0304_0700_0506
AND
0x0808_0808_0808_0808 =
-----------------------------------
0x0000_0000_0000_0000 - НЕТ (нулевой результат)
Код прототипа:
Выражения предельно упрощены, для понимания логики происходящего, и для трассировки алгоритма в отладочном режиме
Алгоритм оптимизирован под инструкцию процессора BSR (Bit Scan Reverse), которая в прототипе дана, как функция "BitOp.bsr64()".
using System;
namespace Queen_8x8
{
delegate void Solution(int[] queens);
class Program
{
static void Main(string[] args)
{
print("Hello Queens!");
print(":");
Queen_8x8 task = new Queen_8x8();
task.smart_check = true;
task.init(print_solution);
task.run();
print("solution_count = " + task.solution_count);
print("solve_count = " + task.solve_count);
print("reverse_count = " + task.reverse_count);
}
static void print(String s)
{
Console.WriteLine(s);
}
static void print_solution(int[] queens)
{
String s = "";
s += "[ ";
for (int i = 0; i < queens.Length; i++)
{
s += Char.ConvertFromUtf32(i + 65) + (queens[i] + 1).ToString();
if (i < (queens.Length - 1)) s += ", ";
}
s += " ]";
print(s);
}
}
class Queen_8x8
{
protected Solution solution;
public const int queens_count = 8;
public const int diag_count = queens_count * 2 - 1;
public ulong markers = 0xFFFF_FFFF_FFFF_FFFF;
public int[] queens = new int[queens_count];
ulong[] diag_LR = new ulong[diag_count];
ulong[] diag_RL = new ulong[diag_count];
ulong attacks_HZ = 0; // атака по горизонтали
ulong attacks_LR = 0; // атака по диагонали BL-TR [\]
ulong attacks_RL = 0; // атака по диагонали BR-TL [/]
public bool smart_check = true;
// Statisticks
public int solution_count = 0;
public int solve_count = 0;
public int reverse_count = 0;
private int get_LR(int x, int y) { return x + y; }
private int get_RL(int x, int y) { return (queens_count - 1 - x) + y; }
public void init(Solution solution)
{
this.solution = solution;
solution_count = 0;
solve_count = 0;
reverse_count = 0;
markers = 0xFFFF_FFFF_FFFF_FFFF;
for (int i = 0; i < queens.Length; i++)
{
queens[i] = -1;
}
for (int i = 0; i < diag_count; i++)
{
diag_LR[i] = 0;
diag_RL[i] = 0;
}
for (int x = 0; x < queens_count; x++)
{
for (int y = 0; y < queens_count; y++)
{
ulong mask = 1UL << ((x << 3) + y);
diag_LR[get_LR(x, y)] |= mask;
diag_RL[get_RL(x, y)] |= mask;
}
}
}
public void run()
{
solve();
}
protected void step(int qx, int qy)
{
ulong q_CM = 0xFFUL << (qx << 3);
ulong a_HZ = 0x0101_0101_0101_0101UL << qy;
ulong a_LR = diag_LR[get_LR(qx, qy)];
ulong a_RL = diag_RL[get_RL(qx, qy)];
// Set Queeen
queens[qx] = qy;
markers &= ~q_CM;
attacks_HZ |= a_HZ;
attacks_LR |= a_LR;
attacks_RL |= a_RL;
// Recurse
solve();
// Remove Queeen
attacks_HZ &= ~a_HZ;
attacks_LR &= ~a_LR;
attacks_RL &= ~a_RL;
markers |= q_CM;
queens[qx] = -1;
}
protected void solve()
{
if (markers == 0)
{
solution_count++;
solution(queens);
return;
}
ulong attacks = attacks_HZ | attacks_LR | attacks_RL;
// Получаем в каждом байте 64-разрядного числа -
// сумму занятых мест по столбцам
// Каждый байт обозначает столбец таблицы и содержит число
// в интервале от 0 до 8
ulong sum_vec_8 = BitOp.popcnt64_bv(attacks);
// Проверка, что остались незаполненные столбцы
// Определяем что в каком либо столбце присуствует число 8
// Если в каком-либо столбце присутствует число 8, то общее значение теста
// станет ненулевым
ulong test = sum_vec_8 & 0x0808_0808_0808_0808UL;
test &= markers; // Отбрасывем столбцы (columns), где уже установлены ферзи
if (smart_check && test != 0)
{
return; // Есть столбец не занятый ферзем, но поставить в этот столбец ферзя - невозможно
}
// Проверка, на то что есть столбцы, только с одим возможным ходом
// Поскольку мы отбросили вариант, что в столбцах присутствует число 8
// прибавляем к каждому столбцу единицу и опять проверяем все столбцы на наличие числа 8
// Если изначально в каком-либо столбце присутствовало число 7, то общее значение теста
// станет ненулевым
test = sum_vec_8 + 0x0101_0101_0101_0101UL;
test &= 0x0808_0808_0808_0808UL;
test &= markers; // Отбрасывем столбцы (columns), где уже установлены ферзи
int qx;
int qy;
ulong column;
if (smart_check && test != 0)
{
reverse_count++;
qx = BitOp.bsr64((test >> 3)) >> 3;
column = (~attacks >> (qx << 3)) & 0xFFUL;
qy = BitOp.bsr64(column);
step(qx, qy);
return;
}
// Делаем перебор по столбцу
qx = BitOp.bsr64(markers) >> 3;
column = (~attacks >> (qx << 3)) & 0xFFUL;
while (column != 0)
{
solve_count++;
qy = BitOp.bsr64(column);
column &= ~(1UL << qy);
step(qx, qy);
}
return;
}
}
class BitOp
{
// Просумировать все биты в байтах 64-разрядного числа
public static ulong popcnt64_bv(ulong value)
{
ulong result = value;
result = result - ((result >> 1) & 0x5555_5555_5555_5555UL); // Результат сумм по 2-а бита
result = (result & 0x3333_3333_3333_3333UL) + ((result >> 2) & 0x3333_3333_3333_3333UL); // Результат сумм по 4-е бита
result = (result + (result >> 4)) & 0x0F0F_0F0F_0F0F_0F0F; // Результат сумм по 8-ь бит
return result;
}
public static byte add64_bv(ulong value)
{
ulong result = value;
result += result >> 8; // Результат сумм по 16-ь бит
result += result >> 16; // Результат сумм по 32-ь бит
result += result >> 32; // Результат
return (byte)(result);
}
/*
* Подсчитать кол-во битов установленных в 1 в 64-разрядном числе
* Полностью эквивалентна машинной инструкции Intel x86/x64 - POPCNT
*/
public static byte popcnt64(ulong value)
{
ulong result = value;
result = result - ((result >> 1) & 0x5555_5555_5555_5555UL); // Результат сумм по 2-а бита
result = (result & 0x3333_3333_3333_3333UL) + ((result >> 2) & 0x3333_3333_3333_3333UL); // Результат сумм по 4-е бита
result = (result + (result >> 4)) & 0x0F0F_0F0F_0F0F_0F0F; // Результат сумм по 8-ь бит
result += result >> 8; // Результат сумм по 16-ь бит
result += result >> 16; // Результат сумм по 32-ь бит
result += result >> 32; // Результат
return (byte)(result);
}
public static byte popcnt8(byte value)
{
ulong result = value;
result = result - ((result >> 1) & 0x55); // Результат сумм по 2-а бита
result = (result & 0x33) + ((result >> 2) & 0x33); // Результат сумм по 4-е бита
result = (result + (result >> 4)) & 0x0F; // Результат сумм по 8-ь бит
return (byte)(result);
}
public static int bsr64(ulong value)
{
if (value == 0) return -1;
int bitpos = 0;
ulong mask = 0xFFFF_FFFF_FFFF_FFFFUL;
int step = 64;
while ((step >>= 1) > 0)
{
if ((value & (mask >>= step)) == 0)
{
value >>= step;
bitpos |= step;
}
}
return bitpos;
}
}
}
Результат программы:

В консоли видно эталонное число найденных комбинаций равное 92, и количество переборов равное 672.
В прототипе присутствует флажок-переменная "smart_check". Установка его в FALSE приведет к отключению моей оптимизации. Тогда вывод в консоль станет классическим.

2056 ./ 672 = 3,05
Оптимизация на количестве переборов выше в 3-и раза.
P.S. Продолжение возможно последует...
UPDATE!!! 27/07/2022
P.P.S. Уже появилась уточненная версия алгоритма (1а), где дополнительно анализируются не только колонки, но и строки, на возможность поставить в них ферзя или поставить единственно возможного ферзя. На данный момент вывод результата выглядит, так:

Упало количество ходов перебора (-80) и реверс-шагов (-140).
Комментарии (29)

PahanMenski
27.07.2022 06:29+2В современном .Net есть класс BitOperations, имеющий методы PopCount и LeadingZeroCount. Если процессор поддерживает инструкции popcnt и lzcnt/bsr соответственно, то эти методы работают как интринсики и JIT компилирует их напрямую в соответствующие инструкции процессора.
Также можно вызывать данные интринсики напрямую, но BitOperations обеспечивает fallback на оптимизированную программную реализацию, если процессор их не поддерживает.

nuzha Автор
27.07.2022 12:29Увы! Мне не удалось подключить BitOperations на момент написания прототипа. Итоговый вариант будет дополнительно сопровождаться исходником на MS C++. Я выбрал C# для быстрого прототипирования. На данный момент, код уже подвергся сильной модифакации, по сравнению с данным исходником.

kipar
27.07.2022 14:08+1Доска симметричная, так что можно искать только решения где в первом столбце ферзь стоит на клетках от a1 до a4, а дальше удвоить результат (отразив доску по вертикали мы получим столько же решений для ферзя от a5 до a8).
Аналогично, можно потребовать чтобы после первых 4 столбцов в 1 строке оказался ферзь, а потом удвоить число решений отразив доску по горизонтали.а нет, не так всё просто. Ведь эти два критерия не независимы.
nuzha Автор
27.07.2022 14:20Я это знаю. И в первом наброске - это присутствовало (A1-A4). Я удалил этот код. Кол-во переборов по схеме A1-A4 равняется 592/2=296 по алгоритму 1а.
Я достиг своего начального предположения, что кол-во шагов перебора не будет превышать 300. Теперь надо постараться снизить и это количество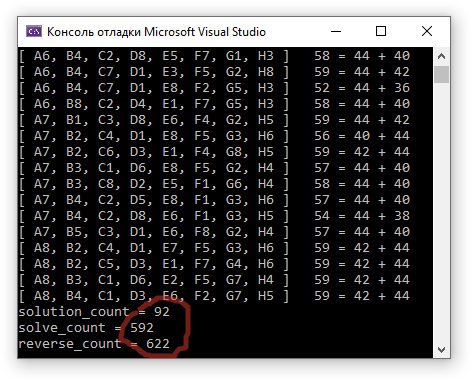
Алгоритм 1а

ShashkovS
27.07.2022 14:58+2Что-то у вас получилось очень сложно. Обычный перебор с возвратом работает здесь очень хорошо: идём по столбцам, храним позиции ферзей в предыдущих столбцах, а также занятые строки и диагонали. Бонусом в первом столбце ферзя ставим только в верхней половине доски, что ускоряет код в два раза.
Код на медленном cPython: доска 8×8 за 0.000655с, доска 12×12 за 0.302с, доска 14×14 за 10 секунд на cPython и за 2 секунды на PyPy.
У вас есть возможность запустить ваш код на досках 12×12? Какое время работы?Код на питонеfrom time import perf_counter def queens(n, cur_column=None, all_positions=None, pos_in_prev_columns=None, used_rows=None, used_diags1=None, used_diags2=None): # При стартовом вызове заполняем все необходимые массивы if cur_column is None: cur_column = 0 all_positions = [] # Список всех найденных позиций pos_in_prev_columns = [] used_rows = [False] * n # Список ферзей в предыдущих столбцах (True=занято) used_diags1 = [False] * (2 * n - 1) # Список занятых диагоналей первого типа used_diags2 = [False] * (2 * n - 1) # Список занятых диагоналей второго типа # В первом столбце перебираем только верхнюю половину доски, дальше по симметрии. Ускоряет в 2 раза if cur_column == 0: check_rows_in_this_column = (n + 1) // 2 else: check_rows_in_this_column = n for row_num in range(check_rows_in_this_column): # Если горизонталь или диагональ заняты, идём дальше if used_rows[row_num] or used_diags1[row_num + cur_column] or used_diags2[row_num - cur_column]: continue # Если дошли до конца, то это победа! elif cur_column == n - 1: all_positions.append(pos_in_prev_columns + [row_num]) # При необходимости добавляем симметричный вариант if pos_in_prev_columns[0] < n // 2: all_positions.append([n - 1 - x for x in all_positions[-1]]) else: # Стандартный перебор с возвратом. Ставим нового ферзя, запускаем рекурсию, откатываемся used_rows[row_num] = used_diags1[row_num + cur_column] = used_diags2[row_num - cur_column] = True pos_in_prev_columns.append(row_num) queens(n, cur_column + 1, all_positions, pos_in_prev_columns, used_rows, used_diags1, used_diags2) pos_in_prev_columns.pop() used_rows[row_num] = used_diags1[row_num + cur_column] = used_diags2[row_num - cur_column] = False return all_positions n = 8 st = perf_counter() all_pos = queens(n) en = perf_counter() print(f'Всего {len(all_pos)} позиций для доски {n}×{n}') print('time:', '{:.3}'.format(en - st)) for pos in sorted(all_pos): print(', '.join('ABCDEFGHIJKLMNOP'[col_n] + str(row_n + 1) for col_n, row_n in enumerate(pos)))

nuzha Автор
27.07.2022 16:06-1Получилось у меня достаточно просто, для людей разбирающихся в целочисленной арифметике. Ведь я ввел в алгоритм первичный позиционный анализ.
Целью исследования является сокращения числа переборов, так называемая "оптимизация перебора". Также целью публикации является акцентировать внимание читателя на так называемой "битовой магии". Битовой магией владе/ли/ют достаточно известные личности - Брезенхем, Кармак, Абраш...
Я не закончил еще с оптимизацией 8×8. Я на данный вижу несколько новых возможностей для оптимизации перебора.
Как закончу исследования переключусь на доски других размерностей. Для этого просто потребуется кластеризация 64-битной арифметики на N-битную. Ожидается стократный выигрыш перед Pyton (как минимум), ведь все состоит из элементарных процессорных инструкций с минимумом обращений по памяти.

ShashkovS
27.07.2022 16:29Ну ок, для доски 8×8 у вас какое время работы?
Просто битовая «магия» (когда она не нужна сама по себе) хорошо работает, когда чисел много и они не лезут в кеш процессора. Тогда битовые маски, сжатие и т.п. отлично работают. Здесь же хоть и перебор большой, но чисел и bool'ов в любой момент очень мало.
nuzha Автор
27.07.2022 17:27Я по своему огромному опыту знаю, что на C/C++ - всё будет очень угарно. А ведь задачу можно еще и распределить на множестве ядер/процессоров. Можно её и видюху сунуть и в FPGA. Так что вопрос замера скорости у меня пока не возникал.
Еще раз, - первоочередная цель - "оптимизация перебора". И демонстрация целочисленной арифметики, как средства наилучшей реализации по-скорости.

ShashkovS
27.07.2022 17:49Какой смысл в «распределить на множестве ядер/процессоров» и «и видюху сунуть и в FPGA», если нормальный алгоритм на одном ядре на тормозном питоне с доской 8×8 работает за 0.650мс?
Запустил ваш код вот здесь, получается 30мс, что в 10 раз медленнее питона на том же onlinegdb.
Уж не знаю, что вы там оптимизировали, но получилось медленно.
nuzha Автор
27.07.2022 17:57Это потому-что, алгоритм нацелен на C/C++ с применением intrinsic и forceinline. Здесь в статье дан прототип на C#. В этом прототипе идут вызовы функций, которые выделены намеряно демонстративно! Для лучшего понимания читателем.
Каким образом буферизируется вывод на консоль C# и Python? А это время не зависящее от работы алгоритма. Для правильных замеров надо в тестах убирать вывод на консоль. Надо делать оптимизацию "A1-A4". Надо убирать лишние вызовы функций. Надо делать 1000-кратные вызовы алгоритма, и в моем случае не вызывать постоянно функцию init().
Когда я говорил про видюху и FPGA - то естественно подразумевались решения на доске типа 1000x1000 и более.

nuzha Автор
27.07.2022 19:05-1Не может язык с динамической типизацией (Python) работать быстрее, чем алгоритм, где каждая операция представляется соответствующей инструкцией процессора, да еще и однотактной или полутактной(U+V Pipes). Исходник на C++ будет по завершению статьи.

ShashkovS
27.07.2022 19:55+1Так я вообще о другом.
Более эффективный алгоритм на Python'е может быть в 100 раз быстрее неудачного алгоритма на C++ с intrinsic'ами и чем угодно.
ИМХО, ваша реализация неудачная, и даже версия на C++ не обгонит Python.
А на большие доски она вообще очень тяжело масштабируется. А pypy обсчитывает доску 14х14 за 2 секунды.
nuzha Автор
27.07.2022 20:38В чём эффективность Вашего алгоритма? В лобовом переборе? В маркировке атак, через массив? Я маркирую атаки в ЕДИНОМ 64-битном числе и не затрачиваюсь на циклы для установки/снятия атак во время выполнения алгоритма.
Дождитесь версии на C++ пожалуйста, прежде чем делать выводы. Я много раз повторил уже - это прототип для ознакомления с логикой. Я планировал 3 публикации сделать, на эту тему.

nuzha Автор
27.07.2022 21:22
1мс 
Вы меня порядком вымучили сегодня! 0-1мс у меня на процессоре от 2011 года. Вывод в консоль отключен. Перестаньте уже пожалуйста!

ShashkovS
27.07.2022 23:39Ну, я просил время работы 5 сообщений назад.
Я не знаю C#, чтобы не разбираться и оценить алгоритм, хорошо было бы понять хоть что-то про время. Я много раз встречал ситуацию, когда «умный велосипед» работает в 100 раз медленнее обычного.
Пришлось разобраться с запуском C#.
Сделал везде 100000 вызовов без вывода в консоль.
На одну итерацию у меня получается:
C# — 0.1013ms
cPython — 0.6469ms
PyPy — 0.1005ms
Rust — 0.0269ms (клон python-решения)
Вот теперь понятен масштаб и уже интересно, до чего можно оптимизировать.
Только вот лучше на доске 12×12 или 14×14. Иначе получается сравнение 0-1ms и 0-1ms.

heone
27.07.2022 21:24Я ещё в конце 90х, на Паскале на I386SX, находил все комбинации за 12сек, против 4минут на вложенных циклах. Применялся 3D массив 8*8*8, при поиске не угрожающих комбинаций. Сейчас не помню, шагов перебора по моему было 284. Если расстановка предыдущих ферзей не создавала угроз, они копировались на слой выше. Если получалась угроза, опускалось на слой ниже и последний ферзь перемещался на следующую клетку. Конец поиска осуществлялся при достижении верхнего слоя без угроз . Потом найденные комбинации поворачивались на 90, 180 и 270 градусов.

nuzha Автор
27.07.2022 21:39-1Ну... трудно что-либо сказать, если Вы "по памяти" говорите. За основу и меня взята установка ферзей в не угрожающие позиции. Это 2056 вариантов перебора. Я добавил в алгоритм позиционный анализ, что сократило число шагов перебора до 592. Если первого ферзя двигать в пределах [A1-A4] - это 592 / 2 = 296. Все атаки фиксируются битами в 64-битном числе.
Тест выполнения дает 0мс на процессоре от 2011 года. Было бы интересно, если бы восстановили свой алгоритм.

ARad
28.07.2022 05:54+1Не мучайте автора, он оптимизирует алгоритм только для доски 8x8.
Он не собирается писать быстрый алгоритм для других размеров доски.
Там его оптимизации просто не будут работать.
nuzha Автор
28.07.2022 18:03-1На доске 8x8 я хотел изложить концепты. Оптимизации будут работать и на досках другой мерности. Но код будет достаточно огромный, чтобы его размещать в статье. Неужели - это непонятно? Я уже изъял из кода много вещей для статьи, чтобы не загромождать концепт и был подвержен различным замечаниям и полезным советам.
Для других мерностей потребуется кластеризация арифметики. Можно оптимизировать по быстродействию определенные из них. Но данная задача настолько синтетическая и не приносящая практической пользы, что непонятно зачем устраивать вообще весь этот трудоёмкий цирк.
Для супер-мерностей можно прибегнуть к распараллеливанию, шейдерам, FPGA. Только объясните, зачем весь этот балаган нужен?
Эффектов SIMD-байт-вектора хватит до мерности N=127. Для мерностей некратных 8-ми потребуется просто прибавить довесок к числу. Дальше идет переход на слова(2 байта).
ARad
28.07.2022 20:28+1Ваши оптимизации основаны на обработке всех клеток за одну операцию. При других размерах это работать не будет.
И самое главное, у вас полный перебор остался, а значит время поиска растет очень быстро.
Насчет супер-мерностей ничего не понял. Тут нет никаких супер-мерностей, доска всегда двумерна, меняется только ее размер.

nuzha Автор
28.07.2022 22:13-1Вы абсолютно невнимательно смотрели!
1. У меня не осталось полного перебора. Я ввел первичный позиционный анализ. И число переборов значительно сократилось. Я прерываю перебор и делаю реверс-шаги по доске. Реверс-шаг это установка ферзя в единственно возможную позицию на доске. И я обнаруживаю такие ситуации на столбцах и строках. и это собственно моё нововведение/ноухау. Я прерываю линейное прохождение и это отображается в переменной reverse_count. А при помощи 64-разрядной арифметики и SIMD-стиля я делаю это очень быстро. Реверс-ситуация уже может случиться после установки 3-го ферзя. Уже первых три ферзя своими атаками могут образовать строку или столбец, куда можно поставить только одного ферзя.
2. Мои переменные работают в SIMD-стиле. И довольно странно слышать утверждение о том, что они не будут работать на повышенной мерности. Это практически, аналогично как работают MMX/SSE. А они и создавались для обработки больших векторов
Супер-мерности - это доски с очень большим размером. Я только это и имел ввиду. Например 1000x1000
Доска с размером 27 - уже имеет 234,907,967,154,122,528 решений
Вроде и возраст у вас солидный, но каждое высказывание - АХИНЕЯ. Как будто вы сюда потроллить зашли. Абсолютно во всем царит упоротое непонимание. Вы не видите, что написано и сделано. Вы придумываете себе тезисы - и с ними и проводите спор. Ну а я то, тут причём спрашивается. Спорьте сам-с-собой в другом месте.
ARad
29.07.2022 13:59Переход на оскорбления и личности пока игнорирую.
Извиняюсь, что написал про полный перебор, конечно же у вас перебор с отсечениями. У вас сейчас отсечения только когда осталась одна клетка в стороке/столбце, возможно на больших досках будет работать хуже...
Искать строку/столбец с минимальным количеством свободных клеток думаю будет работать несколько лучше на больших досках. Возможно вам надо попробовать такую оптимизацию (ускоряет она алгоритм или замедляет для больших досок надо проверять). Думаю ускорит. Насколько она будет быстрее вашего отсечения тоже надо проверять на больших досках.Может вам сразу писать алгоритм для досок любого размера? И использовать System.Runtime.Intrinsics для ускорения с помощью SIMD инструкций? Иначе я не верю, что ваш код будет полезен при переходе от частного случая.
Также для измерения производительности думаю будет полезно заменить вывод в консоль чем нибудь быстрым... Тогда будет легче сравнивать производительность разных хитростей.
В любом случае пока для решения этой задачи существуюь только алгоритмы переборов. Поэтому их сложность быстро растет даже с отсечениями.
nuzha Автор
29.07.2022 15:08Я пытался объяснить в комментариях под этой статьей, почему я выбрал C# и почему работаю на стандартной доске 8x8.
Если бы я начал делать, как говорите/предлагаете Вы, то сложность бы листинга многократно возросла, что привело бы читателя к "закипанию мозгов". И в таком формате "лишь только немногие" могут прочитать код. А дальше - будет ещё намного сложнее.
Я выбрал формат для наиболее популярного изложения замысла и реализации. Естественно в итоге я построю реализацию на C++ с интринсиками и в том числе для разноразмерных досок.
Из-за ограниченности процессорных инструкций приходится прибегать к различным ухищрениям и дополнением, которые даны в новом алгоритме.
Тут все предельно упростилось бы при помощи FPGA на простейшей и элементарной перекоммутации сигналов (Массово переставить биты в числах), но обычный читатель наверно этого бы не понял.
И дальше будут продолжения по теме "оптимизации перебора".
Так как акцент именно на оптимизации/отсечении!
https://habr.com/ru/post/679738/
Не вникнув в первую версию реализации, еще труднее вникнуть в версию 1a







spirit1984
Смущает то, что даже когда флаг отключен, все равно test вычисляется, т.е. по идее нужно сравнивать два решения - классическое, которое не выполняет хитрые манипуляции с битами, и Ваше. А у Вас получается, что классическое все равно прогоняет вычисления. И да, эти вычисления фактически скрывают в себе проверки, для которых потребовалось бы бегать циклом.
Кроме того, не забывайте, что задача о n-ферзях является NP-полной https://habr.com/ru/post/406423/ - т.е. по сути, как с битами не ухищряйся, кардинально снизить сложность так не получится (поскольку битовые манипуляции по сути заменяют обычный цикл, сделанный типа за одну инструкцию процессора).
nuzha Автор
Со
smart_check так сделано по причине, чтобы не усугублять вложенность блоков (отступ) для демо-примера. По идее нужны две функции с "классикой" и моей оптимизацией. Учту при последующих продолженияхnuzha Автор
BSR-инструкция - не заменяет обычный цикл! Я привел прототип на 64-битной арифметике. Примерно также, BSR-инструкция реализована на вентилях процессора (развернутый цикл из 6 операций)
nuzha Автор
Уже есть второй шаг. Надо аккуратно его прописать. Кол-во переборов и реверсов - снизилось ещё
solution_count = 92
solve_count = 592
reverse_count = 622
Надеюсь будет и 3-й шаг. Заключительный, так сказать