Автор статьи — Иван Морозов, выпускник курса OTUS по Machine Learning.

Всем привет!

Любите ли вы задачи кластеризации? Лично я — да. Они хорошо поддаются визуализации, понятны людям, далеким от математики, и зачастую оказывают быстрое влияние на бизнес процессы.

Однако, при решении задач кластеризации мы можем столкнуться с рядом проблем. Среди которых может быть:

• большая размерность вектора признаков

• отсутствие данных на подмножестве фичей

• зашумленность значений / выбросы и т.д.

В случае, если количество объектов небольшое (и увеличить их естественным образом невозможно), то при неблагоприятном стечении обстоятельств мы можем столкнуться с серьезными проблемами в качестве нашей кластеризации.

Но если количество объектов достаточно большое, возникают вычислительные проблемы, такие как: нехватка ресурсов, скорость выполнения и т.д.

Разберём на примере

Рассмотрим пример, в котором проблема проявляется более наглядно. Допустим, у вас есть некий регион, состоящий из нескольких стран, экономический анализ которых вы хотите провести.

В качестве примера я выбрал страны Центральной Азии. Их немного и новые вряд ли появятся в ближайшее время.

Итого мы имеем 4 страны: Казахстан, Кыргызстан, Узбекистан, Таджикистан.

(*Я намеренно убрал из этого списка Туркменистан. Во-первых, это весьма специфическая страна закрытого типа с нерыночной экономикой и многолетней авторитарной системой правления. Доверять данным, которые предоставляют официальные источники, сложно. К тому же данных, которые имеются в открытом доступе довольно мало и они плохо описаны — Прим. автора*)

Конечно, страны этого региона понятны многим жителям постсоветского пространства и нужды применять математику нет. В таком случае вы можете держать в голове, что работаете с чем-то совсем вам неизвестным. Например, японскими провинциями VIII века.

Данные

В качестве данных я взял официальные данные The World Bank Group. Они включают в себя экономические, социальные и демографические индикаторы по каждой стране за различный период времени в разбивке по годам.

В сыром виде имеем 1445 индикаторов с 1960 по 2021 г.

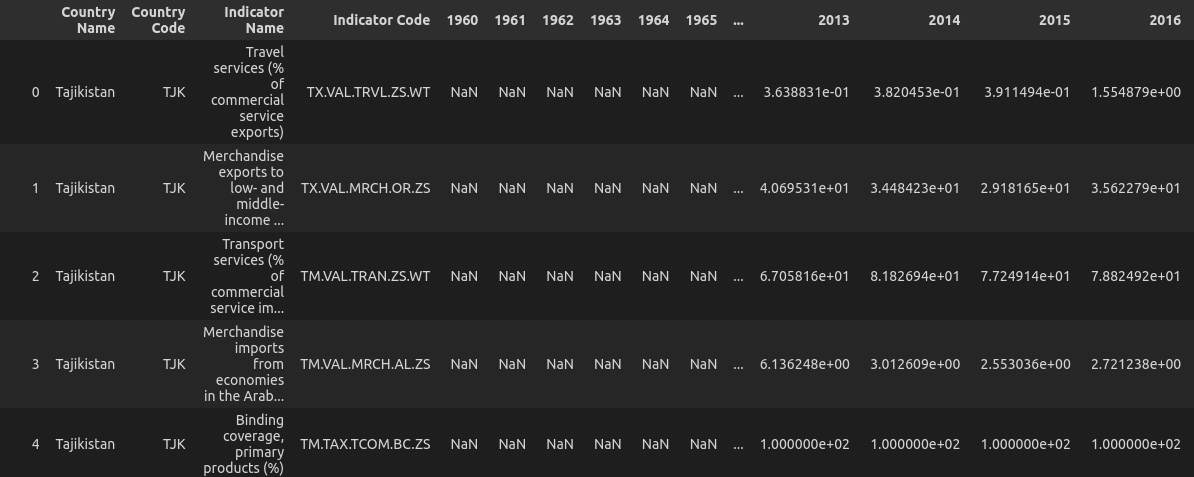
Подготовка нашего датасета будет состоять из несложных правил:

• Рассматриваем данные с 1991 г. (обретения независимости). Получаем 30 значений на один индикатор.

• Не более 5 отсутствующих значений (~16.7% nan).

• Значения индикатора с учетом этих правил должны присутствовать по каждой стране.

Также важно заметить, что наши 5 отсутствующих значений могут присутствовать в какой угодно комбинации: находиться в случайном порядке или подряд, быть в начале ряда или в конце.

*Чуть позже мы увидим, что требования к пропуску в данных могут быть еще ниже, однако на данный момент остановимся на том, что есть.*

У нас получилось 402 индикатора:

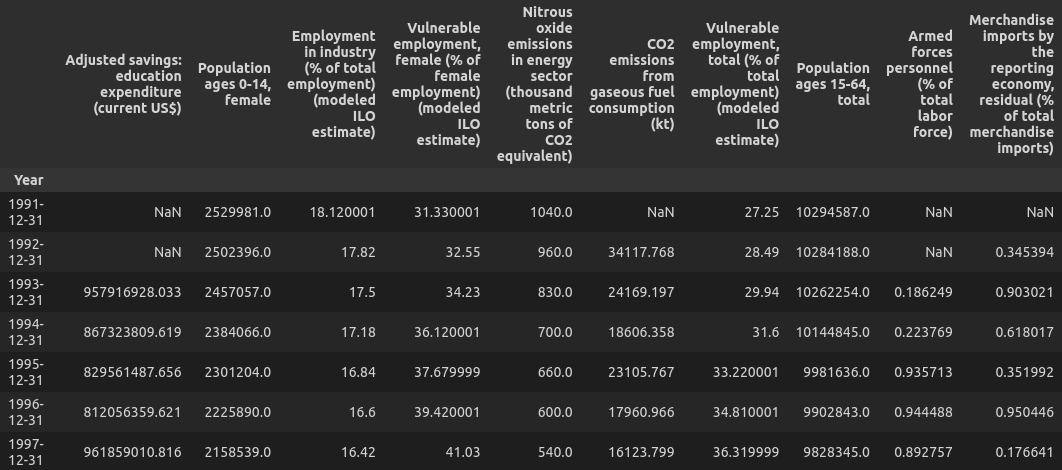
Пропущенные значения я заменил на 0, но как мы увидим позже — это никак не повлияет на результат моделирования.

Давайте визуализируем наши индикаторы:

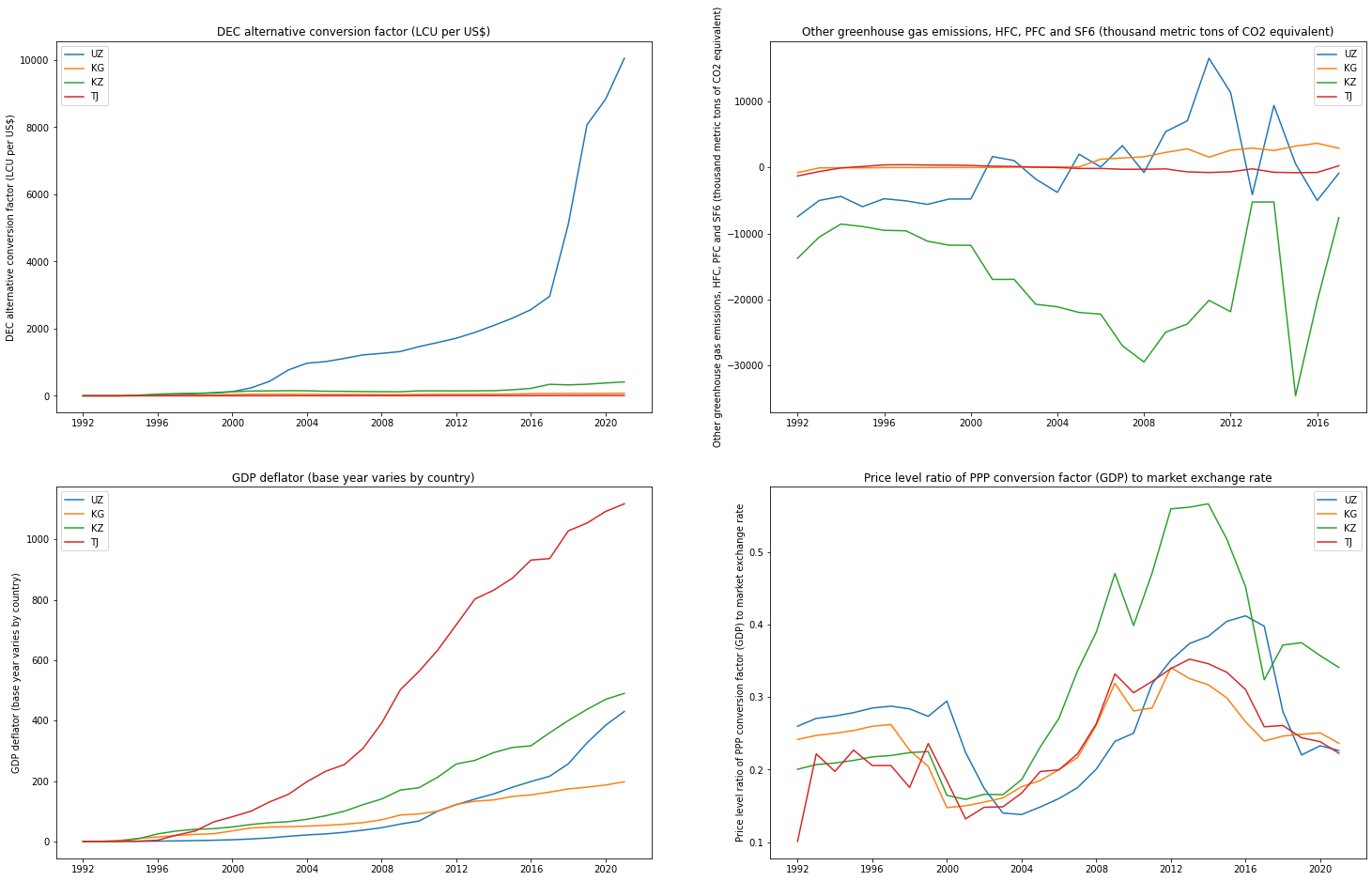
Выглядит как каша, в которой сложно разобраться. Это нам и нужно.

Подходы к решению

Итак, проблема ясна, количество и качество данных тоже.

Прежде чем сформулировать гипотезу, которая нас интересует, давайте взглянем на различные подходы к решению этой задачи и попытаемся выявить скрытые пробелемы, которые за этим стоят.

Экспертная оценка

С одной стороны, мы могли бы прийти с этой задачай к экономисту, эксперту в данной области и попросить его ответить на все наши вопросы. Однако на этом этапе мы встречаем несколько сложностей:

1. Далеко не всегда эксперты едины во мнении относительно того или иного вопроса

2. Стоимость работы эксперта очень высока и хотелось бы использовать его более эффективно. Например, помочь разобраться в причинах выявленных нами явлений (т.к. они могут лежать в иной плоскости)

3. Для ряда проблем существует очень небольшое количество экспертов, а в некотором случае их может не быть вовсе.

Как видим, применение этого варианта существенно зависит от конкретной проблемы и ее специфики.

Экономические

Если экспертная оценка не подходит — почему бы нам не выделить один ключевой индикатор и анализировать четыре временных ряда по одному параметру?

Первое, что может помешать — очень сложно выделить ведущий индикатор. Один отражает экономику, но не качество здравоохранения, другой не учитывает уровень счастья граждан, третий — коррупцию и т.д.

Предположим, что мы могли бы выделить такой индикатор. Пусть это будет ВВП.

Однако даже один индикатор имеет большую специфику расчета, что позволяет получить абсолютно противоречащие друг другу результаты.

В качестве примера:

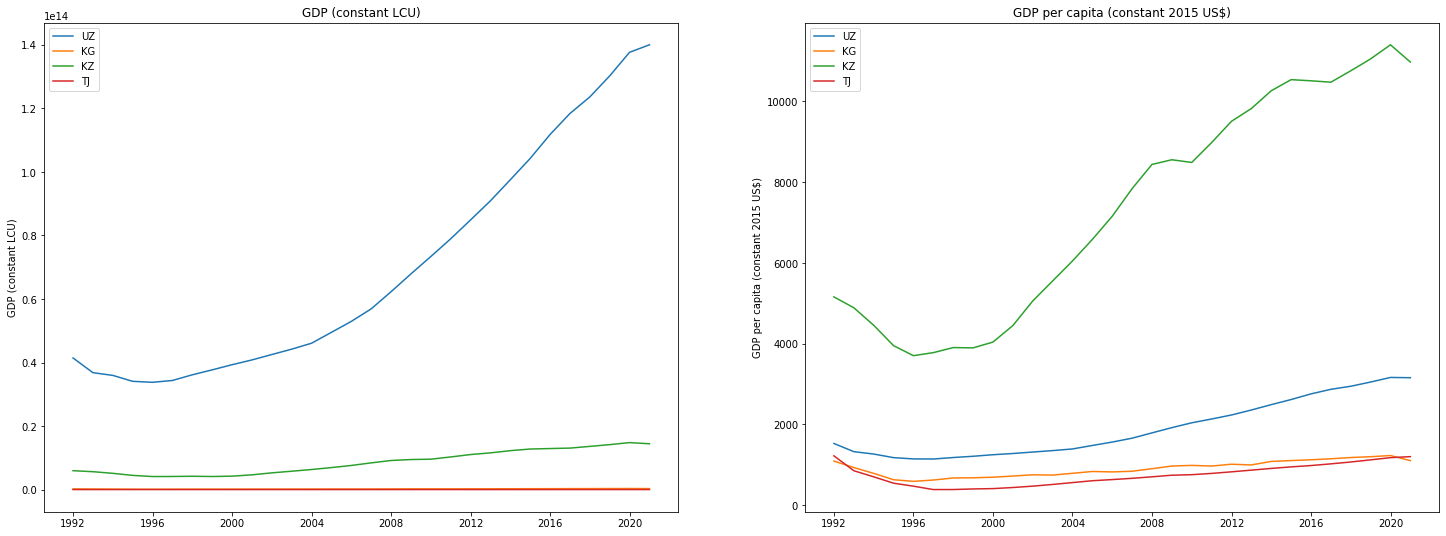
Пример немного высосан из пальца, но он хорошо показывает риски такого подхода.

Математические

Что ж, возможно, нам могут прийти на помощь коробочные решения машинного обучения. Склеив все индикаторы в один вектор размерности 12060 по каждой стране соответственно.

При помощи PCA попробуем сократить размерность до 2 и визуализировать:

Кыргызстан и Таджикистан образуют единый кластер, Казахстан и Узбекистан равноудалены от него и друг друга. Прекрасно!

Попробуем посмотреть на аналогичную визуализацию, сделанную через KMeans

Кыргызстан и Таджикистан снова очень близки друг к другу, Узбекистан максимально удален.

Но как быть с Казахстаном? Он представляет собой отдельный кластер? Относится к паре «Кыргызстан, Таджикистан»? Разумеется, при необходимости можно подобрать параметры под любой желаемый ответ.

Как видим, подобный подход может внести небольшую ясность (например, понятно, какие страны очень близки друг к другу). Однако, остаются вопросы, при решении которых хотелось бы получить большую уверенность. А может быть, задача вообще нерешаемая?

Попробуем описать имеющиеся проблемы:

• Противоречивые результаты не тольо в зависимости от выбора метода анализа, но даже внутри одного и того же.

• В большинстве случаев результаты не интерпретируемые (тот же PCA).

• Низкое количество векторов, высокая размерность (в нашем случае всего 12к, но что если будут миллионы?)

• Высокая чувствительность к данным, шумам, nan и т.д.

• Низкая уверенность в полученных результатах.

Формализуем проблему

Теперь, зная, откуда произрастает проблема и основные трудности, мы можем формализовать ее таким образом, чтобы выдвинуть гипотезу, которую можно однозначно проверить.

Итак: Пусть имеется набор векторов v_1, v_2, ... v_n c размерностью n, где n>>2. Тогда кластеризацию векторов можно заменить на ансамблирование кластеризаций подмножеств их признаков.

Опишем идею еще раз. У нас есть очень большие векторы, которые мы хотим кластеризовать. В таком случае мы можем взять случайное подмножество признаков, кластеризовать их, запомнить результаты кластеризации. Повторив эту операцию определенное количество раз, мы сможем посчитать самый частый случай и считать его итоговой правильной кластеризацией наших объектов (несмотря на то, что все объекты целиком не рассматривались).

Анализ литературы

Фактически, мы только что сформулировали бэггинг для задачи кластеризации. Но можно ли так делать? Приведет ли подобный метод к решению?

К счастью, эта идея была рассмотрена до нас.

Теоретические основы и устойчивость таких разбиений были подробно исследованы в работах *Cristian Hennig*:

1. Hennig, C. (2008) Dissolution point and isolation robustness: robustness criteria for general cluster analysis methods. Journal of Multivariate Analysis, 99, 1154-1176.

2. Hennig, C. (2007) Cluster-wise assessment of cluster stability. Computational Statistics and Data Analysis, 52, 258-271.

Несомненно, наш случай — кластеризация векторов состоящих из временных рядов — является частным случаем рассмотренных задач. Тем не менее, она заслуживает отдельного рассмотрения, обладая рядом особенностей, которые важные для интерпретируемости в прикладных задачах:

• Разбиение вектора возможно исключительно на конкретные подмножества (только по границам индикаторов);

• Bootstrap-техники невозможны, так как они исключают интерпретируемость (за 2016 год возьмем ВВП, за 2017 — безработицу и т.д.);

• Упорядоченность значений внутри разбиения (особенности временных рядов).

Особенности нашей задачи

Таким образом, можно определить специфику и особенности нашего конкретного случая:

• Разбиение на непересекающиеся подмножества (индикаторы)

• Каждое подмножество одинаковой длины (30)

• Кластеризация каждой итерации абсолютна интерпретируема

Также важно заметить, что в данном случае я не ограничиваю количество кластеров, может быть что угодно — 1 vs 3, 2 vs 2 и т.д.

Запускаем эксперимент

Алгоритм действий

Для начала проговорим еще раз, что мы буем делать:

1. Выбираем экономический индикатор (суть временной ряд) из тех, которые еще не анализировали.

2. Кластеризуем наши 4 вектора.

3. Записываем, кто в каком кластере оказался.

4. Повторяем до тех пор, пока не закончатся индикаторы.

5. По итогам считаем, как были кластеризованы наши вектора чаще всего.

Разумеется, мы учитываем не сами метки кластеров, а общую ситуацию.

Посмотрим на результат

Важно заметить, что в 4 случаях я работал с данными, как с временными рядами, используя предобработку таким образом, чтобы учесть варианты, к которым временные ряды особенно чувствительны. Но даже использование классического KMeans, который ничего не знал о характере данных, привел ровно к тому же результату.

*На самом деле я гораздо больше игрался, комбинируя различные варианты, однако всегда получал одну и ту же картину. Единственное, что требует осторожности при использовании t-SNE, т.к. данный алгоритм имеет определенные особенности, касающиеся сохранения исходных расстояний при определенных гиперпараметрах и количестве итераций.*

Отлично, мы увидели, что такой подход весьма устойчив к алгоритмам предобработки и кластеризации. Но как быстро он сходится к итоговому решению, которое будет «усточиво»?

Устойчивость решения

Для этого слегка модифицируем эксперимент — будем брать индикаторы в случайной последовательности и после каждой итерации смотреть на долю каждого варианта (для удобства я взял 3 самых частых).

Если нам повезет, то кластеризация пройдет максимально чисто и «красиво»:

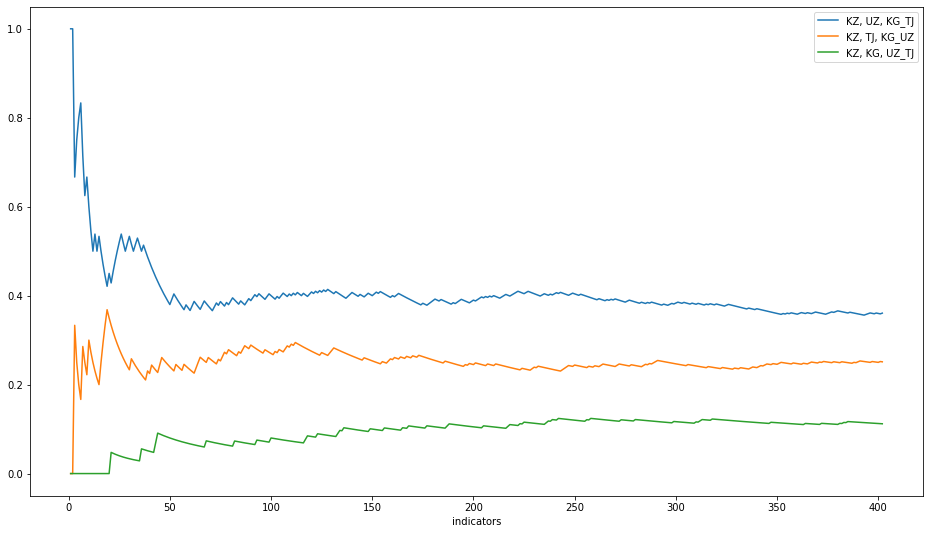
Но, скорее всего, потребуется набрать определенное количество итераций, чтобы быть уверенными:

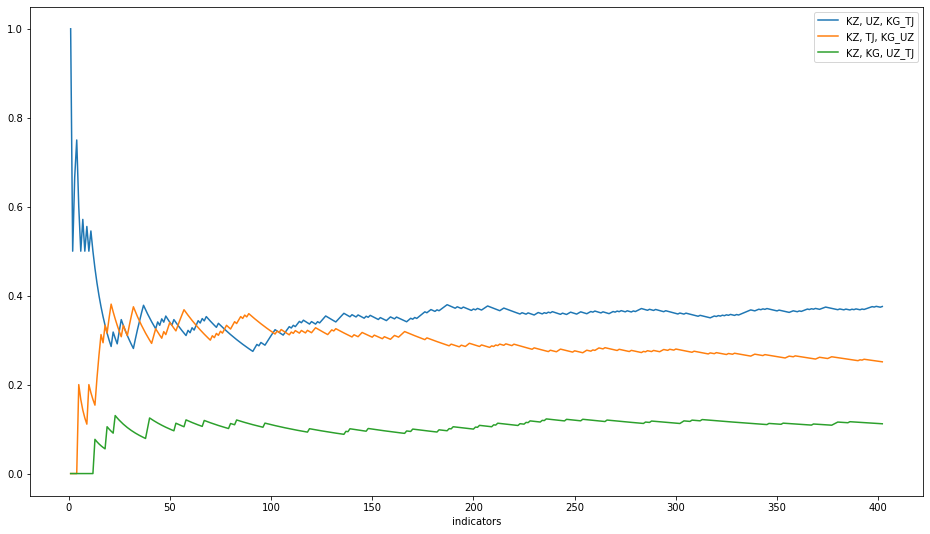
Какими методами определять, что решение устойчиво — каждый может решить самостоятельно, благо их достаточное количество и каждый имеет свои плюсы и минусы.

Разумеется, выбор алгоритма может повлиять на худший случай. Однако, я не смог получить ни одного случая, когда разделение не было бы устойчивым после 150 итераций (37.3%). При небольшом исследовании и грамотном подходе это число сократится до ~20-22%.

Это значит, что мы можем допустить ~62.7% - 80% невалидных значений (пропуски, шумы и т.д.) для того, чтобы уверенно кластеризовать наши объекты.

Проверим результаты

В качестве проверки, верны ли наши результаты, обратимся к экспертным оценкам и профильным журналам. Я взял несколько из них, стараясь выбирать объективные. Материалы статей в открытом доступе, желающие могут с ними ознакомиться самостоятельно.

1. «Экономика центральной азии»; исследовательская компания BRIF Research Group.

2. «Почему на экономику Центральной Азии нужно взглянуть по-новому»; Евгений Винокуров, главный экономист Евразийского банка развития и Евразийского фонда стабилизации и развития.

3. «Таджикистан и Кыргызстан: традиции добрососедства и перспективы миростроительства»; Central Asian Bureau for Analytical Reporting.

От себя лишь скажу, что данные статьи сделанны людьми, корошо знающими регион, полностью подтверждают полученные нами результаты.

Выводы

Подходя к финальной части статьи, хотелось бы выделить основные плюсы данного подхода:

• Сокращение количества «фичей» для кластеризации;

• Снижение требований к качеству данных (в нашем случае до 80% данных могут отсутствовать);

• Повышение скорости кластеризации для огромных векторов;

• Уменьшение использования ресурсов;

• Интерпретируемость результатов.

Приглашаем всех желающих на открытое занятие «Пишем свою первую нейронную сеть». На занятии мы рассмотрим основные этапы создания и обучения своей первой нейронной сети и попробуем решить известную задачу классификации MNIST полносвязной и сверточной нейронными сетями на примере фреймворка PyTorch. Регистрация доступна по ссылке.

Также в середине августа состоится бесплатный двухдневный интенсив, посвященный ансамблированию моделей — крайне популярной технике ML, позволяющей построить сильные модели на основе простых базовых алгоритмов. В 1ый день участники познакомятся с методами Bagging и Random forest и применят их на практике. Во 2ой день день — познакомятся с градиентным бустингом и попробуют на практике этот один из наиболее популярных алгоритмов Kaggle. Запись на интенсив.