Постановка задачи

При статистическом анализе зависимостей между количественными переменными возникают ситуации, когда представляет интерес расчет и анализ такого показателя как корреляционное отношение (η).

Данный показатель незаслуженно обойден вниманием в большинстве доступных для пользователей математических пакетов.

В данном разборе рассмотрим способы расчета и анализа η средствами Python.

Не будем углубляться в теорию (про η достаточно подробно написано, например, в [1, с.73], [2, с.412], [3, с.609]), но вспомним основные свойства η:

1. η характеризует степень тесноты любой корреляционной связи (как линейной, так и нелинейной), в отличие от коэффициента корреляции Пирсона r, который характеризует тесноту только линейной связи. Условие r=0 означает отсутствие линейной корреляционной связи между величинами, но при этом между ними может существовать нелинейная корреляционная связь (η>0).

2. η принимает значения от 0 до 1; при η=0 корреляционная связь отсутствует, при η=1 связь считается функциональной; степень тесноты связи можно оценивать по различным общепринятым шкалам, например, по шкале Чеддока и др.

3. Величина η² характеризует долю вариации, объясненной корреляционной связью между рассматриваемыми переменными.

4. η не может быть меньше абсолютной величины r: η ≥ |r|.

5. η несимметрично по отношению к исследуемым переменным, то есть η_XY ≠ η_YX.

6. Для расчета η необходимо иметь эмпирические данные эксперимента с повторностями; если же мы имеем просто два набора значений переменных X и Y, то данные нужно группировать. Этот вывод, в общем-то, очевиден - если предпринять попытку рассчитать η по негруппированным данным, получим результат η=1.

Группировка данных для расчета η заключается в разбиении области значений переменных X и Y на интервалы, подсчет частот попадания данных в интервалы и формирование корреляционной таблицы.

Важное замечание: особенности методики расчета корреляционного отношения, особенно при форме связи, близкой к линейной, и η близком к единице, могут привести к результатам, в общем-то абсурдным, например:

• когда нарушается условие η ≥ |r|;

• когда r окажется значим, а η нет;

• когда нижняя граница доверительного интервала для η окажется меньше 0 или верхняя граница - больше 1.

Это нужно учитывать при выполнении анализа.

Итак, перейдем к расчетам.

Формирование исходных данных

В качестве исходных данных рассмотрим зависимость расхода среднемесячного расхода топлива автомобиля (л/100 км) (FuelFlow) от среднемесячного пробега (км) (Mileage).

Загрузим исходные данные из csv-файла (исходные данные доступны в моем репозитории на GitHub):

fuel_df = pd.read_csv(
    filepath_or_buffer='data/fuel_df.csv',
    sep=';',
    index_col='Number')
dataset_df = fuel_df.copy()    # создаем копию исходной таблицы для работы
display(dataset_df.head())

Загруженный DataFrame содержит следующие столбцы:

• Month — месяц (в формате Excel)

• Mileage - месячный пробег (км)

• Temperature - среднемесячная температура (°C)

• FuelFlow - среднемесячный расход топлива (л/100 км)

Сохраним нужные нам переменные Mileage и FuelFlow в виде numpy.ndarray.

X = np.array(dataset_df['Mileage'])
Y = np.array(dataset_df['FuelFlow'])

Для удобства дальнейшей работы сформируем сформируем отдельный DataFrame из двух переменных - X и Y:

data_XY_df = pd.DataFrame({
    'X': X,
    'Y': Y})

Настройка заголовков отчета (для дальнейшего формирования графиков):

# Общий заголовок проекта
Task_Project = "Расчет и анализ корреляционного отношения средствами Python"
# Заголовок, фиксирующий момент времени
AsOfTheDate = ""
# Заголовок раздела проекта
Task_Theme = "Анализ расхода топлива автомобиля"
# Общий заголовок проекта для графиков
Title_String = f"{Task_Project}\n{AsOfTheDate}"
# Наименования переменных
Variable_Name_X = "Среднемесячный пробег (км)"
Variable_Name_Y = "Среднемесячный расход топлива автомобиля (л/100 км)"

Визуализация и первичная обработка данных

Предварительно отсеем аномальные значения (выбросы). Подробно не будем останавливаться на этой процедуре, она не является целью данного разбора.

mask1 = data_XY_df['X'] > 200
mask2 = data_XY_df['X'] < 2000
data_XY_df = data_XY_df[mask1 & mask2]

X = np.array(data_XY_df['X'])
Y = np.array(data_XY_df['Y'])

Описательная статистика исходных данных:

data_XY_df.describe()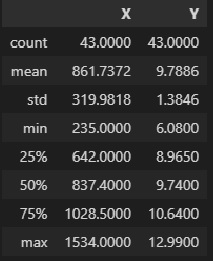

Выполним визуализацию исходных данных:

fig, axes = plt.subplots(figsize=(297/INCH, 210/INCH))
fig.suptitle(Task_Theme)
axes.set_title('Зависимость расхода топлива от пробега')
data_df = data_XY_df
sns.scatterplot(
    data=data_df,
    x='X', y='Y',
    label='эмпирические данные',
    s=50,
    ax=axes)
axes.set_xlabel(Variable_Name_X)
axes.set_ylabel(Variable_Name_Y)
#axes.tick_params(axis="x", labelsize=f_size+4)
#axes.tick_params(axis="y", labelsize=f_size+4)
#axes.legend(prop={'size': f_size+6})
plt.show()
fig.savefig('graph/scatterplot_XY_sns.png', orientation = "portrait", dpi = 300)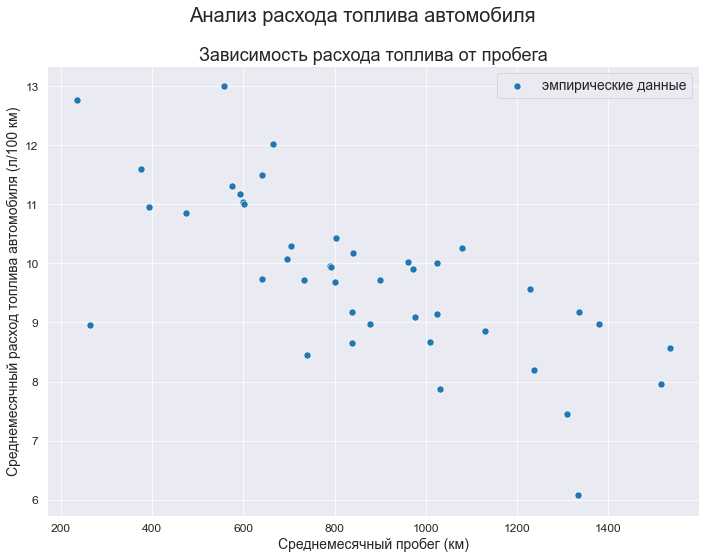

Для визуальной оценки выборочных данных построим гистограммы и коробчатые диаграммы:

fig = plt.figure(figsize=(420/INCH, 297/INCH))
ax1 = plt.subplot(2,2,1)
ax2 = plt.subplot(2,2,2)
ax3 = plt.subplot(2,2,3)
ax4 = plt.subplot(2,2,4)
fig.suptitle(Task_Theme)
ax1.set_title('X')
ax2.set_title('Y')

# инициализация данных
data_df = data_XY_df
X_mean = data_df['X'].mean()
X_std = data_df['X'].std(ddof = 1)
Y_mean = data_df['Y'].mean()
Y_std = data_df['Y'].std(ddof = 1)
bins_hist = 'sturges'    # выбор числа интервалов ('auto', 'fd', 'doane', 'scott', 'stone', 'rice', 'sturges', 'sqrt')

# данные для графика плотности распределения X
xmin = np.amin(data_df['X'])
xmax = np.amax(data_df['X'])
nx = 100
hx = (xmax - xmin)/(nx - 1)
x1 = np.linspace(xmin, xmax, nx)
xnorm1 = sps.norm.pdf(x1, X_mean, X_std)
kx = len(np.histogram(X, bins=bins_hist, density=False)[0])
xnorm2 = xnorm1*len(X)*(xmax-xmin)/kx

# данные для графика плотности распределения Y
ymin = np.amin(Y)
ymax = np.amax(Y)
ny = 100
hy = (ymax - ymin)/(ny - 1)
y1 = np.linspace(ymin, ymax, ny)
ynorm1 = sps.norm.pdf(y1, Y_mean, Y_std)
ky = len(np.histogram(Y, bins=bins_hist, density=False)[0])
ynorm2 = ynorm1*len(Y)*(ymax-ymin)/ky

# гистограмма распределения X
ax1.hist(
    data_df['X'],
    bins=bins_hist,
    density=False,
    histtype='bar',    # 'bar', 'barstacked', 'step', 'stepfilled'
    orientation='vertical',   # 'vertical', 'horizontal'
    color = "#1f77b4",
    label='эмпирическая частота')
ax1.plot(
    x1, xnorm2,
    linestyle = "-",
    color = "r",
    linewidth = 2,
    label = 'теоретическая нормальная кривая')
ax1.axvline(X_mean, color='magenta', label = 'среднее значение')
ax1.axvline(np.median(data_df['X']), color='orange', label = 'медиана')
ax1.legend(fontsize = f_size+4)

# гистограмма распределения Y
ax2.hist(
    data_df['Y'],
    bins=bins_hist,
    density=False,
    histtype='bar',    # 'bar', 'barstacked', 'step', 'stepfilled'
    orientation='vertical',   # 'vertical', 'horizontal'
    color = "#1f77b4",
    label='эмпирическая частота')    
ax2.plot(
    y1, ynorm2,
    linestyle = "-",
    color = "r",
    linewidth = 2,
    label = 'теоретическая нормальная кривая')
ax2.axvline(Y_mean, color='magenta', label = 'среднее значение')
ax2.axvline(np.median(data_df['Y']), color='orange', label = 'медиана')
ax2.legend(fontsize = f_size+4)

# коробчатая диаграмма X
sns.boxplot(
    #data=corn_yield_df,
    x=data_df['X'],
    orient='h',
    width=0.3,
    ax=ax3)

# коробчатая диаграмма Y
sns.boxplot(
    #data=corn_yield_df, 
    x=data_df['Y'], 
    orient='h', 
    width=0.3, 
    ax=ax4)

# подписи осей 
ax3.set_xlabel(Variable_Name_X)
ax4.set_xlabel(Variable_Name_Y)

plt.show()
fig.savefig('graph/scatterplot_boxplot_X_Y_sns.png', orientation = "portrait", dpi = 300)

Перед тем, как приступать к дальнейшим расчетам, проверим исходные данные на соответствие нормальному закону распределения.

Выполнять такую проверку нужно обязательно, так как только для нормально распределенных данных мы можем в дальнейшем использовать общепринятые статистические процедуры анализа: проверку значимости корреляционного отношения, построение доверительных интервалов и т.д.

 Для проверки нормальности распределения воспользуемся критерием Шапиро-Уилка:

# функция для обработки реализации теста Шапиро-Уилка
def Shapiro_Wilk_test(data):
    data = np.array(data)
    result = sci.stats.shapiro(data)
    s_calc = result.statistic    # расчетное значение статистики критерия
    a_calc = result.pvalue    # расчетный уровень значимости
    
    print(f"Расчетный уровень значимости: a_calc = {round(a_calc, DecPlace)}")
    print(f"Заданный уровень значимости: a_level = {round(a_level, DecPlace)}")
    
    if a_calc >= a_level:
        conclusion_ShW_test = f"Так как a_calc = {round(a_calc, DecPlace)} >= a_level = {round(a_level, DecPlace)}" + \
            ", то гипотеза о нормальности распределения по критерию Шапиро-Уилка ПРИНИМАЕТСЯ"
    else:
        conclusion_ShW_test = f"Так как a_calc = {round(a_calc, DecPlace)} < a_level = {round(a_level, DecPlace)}" + \
            ", то гипотеза о нормальности распределения по критерию Шапиро-Уилка ОТВЕРГАЕТСЯ"
    print(conclusion_ShW_test)

# проверка нормальности распределения переменной X
Shapiro_Wilk_test(X)

# проверка нормальности распределения переменной Y
Shapiro_Wilk_test(Y)

Итак, гипотеза о нормальном распределении исходных данных принимается, что позволяет нам в дальнейшем пользоваться статистическим инструментарием для интервального оценивания величины η, проверки гипотез и т.д.

Переходим собственно к расчету корреляционного отношения.

Переходим собственно к расчету корреляционного отношения.

Расчёт и анализ корреляционного отношения

1. Выполним группировку исходных данным по обоим признакам X и Y:

Создадим новую переменную matrix_XY_df для работы с группированными данными:

matrix_XY_df = data_XY_df.copy()

Определим число интервалов группировки (воспользуемся формулой Стерджесса); при этом минимальное число интервалов должно быть не менее 2:

# объем выборки для переменных X и Y
n_X = len(X)
n_Y = len(Y)

# число интервалов группировки
group_int_number = lambda n: round (3.31*log(n_X, 10)+1) if round (3.31*log(n_X, 10)+1) >=2 else 2

K_X = group_int_number(n_X)
K_Y = group_int_number(n_Y)
print(f"Число интервалов группировки для переменной X: {K_X}")
print(f"Число интервалов группировки для переменной Y: {K_Y}")

Выполним группировку данных средствами библиотеки pandas, для этого воспользуемся функцией pandas.cut. В результате получим новые признаки cut_X и cut_X, которые показывают, в какой из интервалов попадает конкретное значение X и Y. Полученные новые признаки добавим в DataFrame matrix_XY_df:

cut_X = pd.cut(X, bins=K_X)
cut_Y = pd.cut(Y, bins=K_Y)

matrix_XY_df['cut_X'] = cut_X
matrix_XY_df['cut_Y'] = cut_Y

display(matrix_XY_df.head())

Теперь мы можем получить корреляционную таблицу с помощью функции pandas.crosstab:

CorrTable_df = pd.crosstab(
    index=matrix_XY_df['cut_X'],
    columns=matrix_XY_df['cut_Y'],
    rownames=['cut_X'],
    colnames=['cut_Y'])

display(CorrTable_df)

# проверка правильности подсчета частот по интервалам
print(f"sum = {np.sum(np.array(CorrTable_df))}")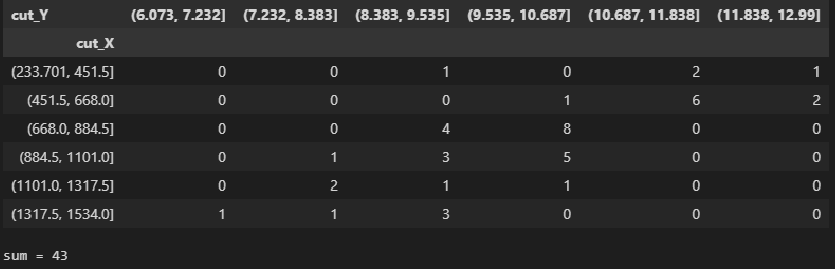

Функция pandas.crosstab также позволяет формировать более ровные и удобные для восприятия границы интервалов группировки путем задания их вручную. Для расчета η это принципиального значения не имеет, но в отдельных случаях может быть полезно.

Например, зададим вручную границы интервалов группировки для X и Y:

bins_X = pd.IntervalIndex.from_tuples([(200, 400), (400, 600), (600, 800), (800, 1000), (1000, 1200), (1200, 1400), (1400, 1600)])
cut_X = pd.cut(X, bins=bins_X)

bins_Y = pd.IntervalIndex.from_tuples([(6.0, 7.0), (7.0, 8.0), (8.0, 9.0), (9.0, 10.0), (10.0, 11.0), (11.0, 12.0), (12.0, 13.0)])
cut_Y = pd.cut(X, bins=bins_Y)

CorrTable_df2 = pd.crosstab(
    index=pd.cut(X, bins=bins_X),
    columns=pd.cut(Y, bins=bins_Y),
    rownames=['cut_X'],
    colnames=['cut_Y'])
display(CorrTable_df2)

# проверка правильности подсчета частот по интервалам
print(f"sum = {np.sum(np.array(CorrTable_df2))}")

Есть и другой способ получения корреляционной таблицы - с помощью pandas.pivot_table:

matrix_XY_df.pivot_table(
    values=['Y'],
    index='cut_X',
    columns='cut_Y',
    aggfunc=len,
    fill_value=0)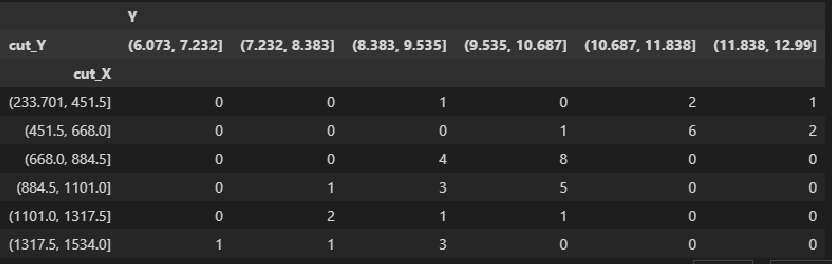

2. Выполним расчет корреляционного отношения:

Для дальнейших расчетов приведем корреляционную таблицу к типу numpy.ndarray:

CorrTable_np = np.array(CorrTable_df)
print(CorrTable_np, type(CorrTable_np))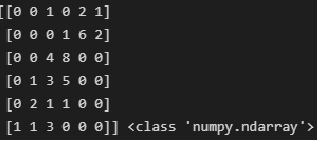

Итоги корреляционной таблицы по строкам и столбцам:

# итоги по строкам
n_group_X = [np.sum(CorrTable_np[i]) for i in range(K_X)]
print(f"n_group_X = {n_group_X}")

# итоги по столбцам
n_group_Y = [np.sum(CorrTable_np[:,j]) for j in range(K_Y)]
print(f"n_group_Y = {n_group_Y}")

Также нам необходимо получить среднегрупповые значения X и Y для каждой группы (интервала). При этом нужно помнить, что функция pandas.crosstab при группировании расширяет крайние диапазоны на 0.1% с каждой стороны, чтобы включить минимальное и максимальное значения.

Для доступа к данным - границам интервалов, полученным с помощью pandas.cut - существуют методы right и left:

# Среднегрупповые значения переменной X
Xboun_mean = [(CorrTable_df.index[i].left + CorrTable_df.index[i].right)/2 for i in range(K_X)]
Xboun_mean[0] = (np.min(X) + CorrTable_df.index[0].right)/2    # исправляем значения в крайних интервалах
Xboun_mean[K_X-1] = (CorrTable_df.index[K_X-1].left + np.max(X))/2
print(f"Xboun_mean = {Xboun_mean}")

# Среднегрупповые значения переменной Y
Yboun_mean = [(CorrTable_df.columns[j].left + CorrTable_df.columns[j].right)/2 for j in range(K_Y)]
Yboun_mean[0] = (np.min(Y) + CorrTable_df.columns[0].right)/2    # исправляем значения в крайних интервалах
Yboun_mean[K_Y-1] = (CorrTable_df.columns[K_Y-1].left + np.max(Y))/2
print(f"Yboun_mean = {Yboun_mean}", '\n')

Находим средневзевешенные значения X и Y для каждой группы:

Xmean_group = [np.sum(CorrTable_np[:,j] * Xboun_mean) / n_group_Y[j] for j in range(K_Y)]
print(f"Xmean_group = {Xmean_group}")

Ymean_group = [np.sum(CorrTable_np[i] * Yboun_mean) / n_group_X[i] for i in range(K_X)]
print(f"Ymean_group = {Ymean_group}")

Общая дисперсия X и Y:

Sum2_total_X = np.sum(n_group_X * (Xboun_mean - np.mean(X))**2)
print(f"Sum2_total_X = {Sum2_total_X}")

Sum2_total_Y = np.sum(n_group_Y * (Yboun_mean - np.mean(Y))**2)
print(f"Sum2_total_Y = {Sum2_total_Y}")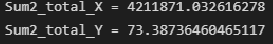

Межгрупповая дисперсия X и Y (дисперсия групповых средних):

Sum2_between_group_X = np.sum(n_group_Y * (Xmean_group - np.mean(X))**2)
print(f"Sum2_between_group_X = {Sum2_between_group_X}")

Sum2_between_group_Y = np.sum(n_group_X * (Ymean_group - np.mean(Y))**2)
print(f"Sum2_between_group_Y = {Sum2_between_group_Y}")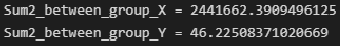

Внутригрупповая дисперсия X и Y (возникает за счет других факторов - не связанных с другой переменной):

print(f"Sum2_within_group_X = {Sum2_total_X - Sum2_between_group_X}")
print(f"Sum2_within_group_Y = {Sum2_total_Y - Sum2_between_group_Y}")

Эмпирическое корреляционное отношение:

corr_ratio_XY = sqrt(Sum2_between_group_Y / Sum2_total_Y)
print(f"corr_ratio_XY = {corr_ratio_XY}")

corr_ratio_YX = sqrt(Sum2_between_group_X / Sum2_total_X)
print(f"corr_ratio_YX = {corr_ratio_YX}")

Итак, мы получили результат - значение корреляционного отношения.

Оценим тесноту корреляционной связи по шкале Чеддока, для удобства создадим пользовательскую функцию:

def Cheddock_scale_check(r, name='r'):
    # задаем шкалу Чеддока
    Cheddock_scale = {
        f'no correlation (|{name}| <= 0.1)':    0.1,
        f'very weak (0.1 < |{name}| <= 0.2)':   0.2,
        f'weak (0.2 < |{name}| <= 0.3)':        0.3,
        f'moderate (0.3 < |{name}| <= 0.5)':    0.5,
        f'perceptible (0.5 < |{name}| <= 0.7)': 0.7,
        f'high (0.7 < |{name}| <= 0.9)':        0.9,
        f'very high (0.9 < |{name}| <= 0.99)':  0.99,
        f'functional (|{name}| > 0.99)':        1.0}
    
    r_scale = list(Cheddock_scale.values())
    for i, elem in enumerate(r_scale):
        if abs(r) <= elem:
            conclusion_Cheddock_scale = list(Cheddock_scale.keys())[i]
            break
    return conclusion_Cheddock_scale

Шкала Чеддока изначально предназначалась для оценки тесноты линейно корреляционной связи (на основе коэффициента корреляции Пирсона r), но мы ее применим и для корреляционного отношения η (не забывая про свойство η ≥ r!). В выводе функции Cheddock_scale_check можно указать символ, обозначающий величину - аргумент name=chr(951) выводит η вместо r.

В современных исследованиях шкала Чеддока теряет популярность, в последние годы все чаще применяется шкала Эванса (в психосоциальных, медико-биологических и др.исследованиях) ( более подробно про шкалы Чеддока, Эванса и др. - см.[4]). Оценим тесноту корреляционной связи по шкале Эванса, для удобства также создадим пользовательскую функцию:

def Evans_scale_check(r, name='r'):
    # задаем шкалу Эванса
    Evans_scale = {
        f'very weak (|{name}| < 0.19)':         0.2,
        f'weak (0.2 < |{name}| <= 0.39)':       0.4,  
        f'moderate (0.4 < |{name}| <= 0.59)':   0.6,
        f'strong (0.6 < |{name}| <= 0.79)':     0.8,
        f'very strong (0.8 < |{name}| <= 1.0)': 1.0}
    
    r_scale = list(Evans_scale.values())
    for i, elem in enumerate(r_scale):
        if abs(r) <= elem:
            conclusion_Evans_scale = list(Evans_scale.keys())[i]
            break
    return conclusion_Evans_scale    

print(f"Оценка тесноты корреляции по шкале Эванса: {Evans_scale_check(corr_ratio_XY, name=chr(951))}")

Итак, степень тесноты корреляционной связи может быть оценена как высокая (по шкале Чеддока), сильная (по шкале Эванса).

3. Проверка значимости корреляционного отношения:

Рассмотрим нулевую гипотезу:

H0: ηXY = 0
H1: ηXY ≠ 0

Для проверки нулевой гипотезы воспользуемся критерием Фишера:

# расчетное значение статистики критерия Фишера
F_corr_ratio_calc = (n_X - K_X)/(K_X - 1) * corr_ratio_XY**2 / (1 - corr_ratio_XY**2)
print(f"Расчетное значение статистики критерия Фишера: F_calc = {round(F_corr_ratio_calc, DecPlace)}")
# табличное значение статистики критерия Фишера
dfn = K_X - 1
dfd = n_X - K_X
F_corr_ratio_table = sci.stats.f.ppf(p_level, dfn, dfd, loc=0, scale=1)
print(f"Табличное значение статистики критерия Фишера: F_table = {round(F_corr_ratio_table, DecPlace)}")
# расчетный уровень значимости
a_corr_ratio_calc = 1 - sci.stats.f.cdf(F_corr_ratio_calc, dfn, dfd, loc=0, scale=1)
print(f"Расчетный уровень значимости: a_calc = {round(a_corr_ratio_calc, DecPlace)}")
print(f"Заданный уровень значимости: a_level = {round(a_level, DecPlace)}")
# вывод
if F_corr_ratio_calc < F_corr_ratio_table:
    conclusion_corr_ratio_sign = f"Так как F_calc = {round(F_corr_ratio_calc, DecPlace)} < F_table = {round(F_corr_ratio_table, DecPlace)}" + \
        ", то гипотеза о равенстве нулю корреляционного отношения ПРИНИМАЕТСЯ, т.е. корреляционная связь НЕЗНАЧИМА"
else:
    conclusion_corr_ratio_sign = f"Так как F_calc = {round(F_corr_ratio_calc, DecPlace)} >= F_table = {round(F_corr_ratio_table, DecPlace)}" + \
        ", то гипотеза о равенстве нулю корреляционного отношения ОТВЕРГАЕТСЯ, т.е. корреляционная связь ЗНАЧИМА"
print(conclusion_corr_ratio_sign)

4. Доверительный интервал для корреляционного отношения:

# число степеней свободы
f1 = round ((K_X - 1 + n_X * corr_ratio_XY**2)**2 / (K_X - 1 + 2 * n_X * corr_ratio_XY**2))
f2 = n_X - K_X
# вспомогательные величины
z1 = (n_X - K_X) / n_X * corr_ratio_XY**2 / (1 - corr_ratio_XY**2) * 1/sci.stats.f.ppf(p_level, f1, f2, loc=0, scale=1) - (K_X - 1)/n_X
z2 = (n_X - K_X) / n_X * corr_ratio_XY**2 / (1 - corr_ratio_XY**2) * 1/sci.stats.f.ppf(1 - p_level, f1, f2, loc=0, scale=1) - (K_X - 1)/n_X
# доверительный интервал
corr_ratio_XY_low = sqrt(z1) if sqrt(z1) >= 0 else 0
corr_ratio_XY_high = sqrt(z2) if sqrt(z2) <= 1 else 1
print(f"{p_level*100}%-ный доверительный интервал для корреляционного отношения: {[round(corr_ratio_XY_low, DecPlace), round(corr_ratio_XY_high, DecPlace)]}")

Важное замечание: при значениях η близких к 0 или 1 левая или правая граница доверительного интервала может выходить за пределы отрезка [0; 1], теряя содержательный смысл (см. [1, с.80]). Причина этого - в аппроксимационном подходе к определению границ доверительного интервала. Подобные нежелательные явления возможны, и их нужно учитывать при выполнении анализа.

5. Проверка значимости отличия линейной корреляционной связи от нелинейной:

Оценим величину коэффициента линейной корреляции:

corr_coef = sci.stats.pearsonr(X, Y)[0]
print(f"Коэффициент линейной корреляции: r = {round(corr_coef, DecPlace)}")

print(f"Оценка тесноты линейной корреляции по шкале Чеддока: {Cheddock_scale_check(corr_coef)}")
print(f"Оценка тесноты линейной корреляции по шкале Эванса: {Evans_scale_check(corr_coef)}")

Проверим значимость коэффициента линейной корреляции:

# расчетный уровень значимости
a_corr_coef_calc = sci.stats.pearsonr(X, Y)[1]
print(f"Расчетный уровень значимости коэффициента линейной корреляции: a_calc = {a_corr_coef_calc}")
print(f"Заданный уровень значимости: a_level = {round(a_level, DecPlace)}")
# вывод
if a_corr_coef_calc >= a_level:
    conclusion_corr_coef_sign = f"Так как a_calc = {a_corr_coef_calc} >= a_level = {round(a_level, DecPlace)}" + \
        ", то гипотеза о равенстве нулю коэффициента линейной корреляции ПРИНИМАЕТСЯ, т.е. линейная корреляционная связь НЕЗНАЧИМА"
else:
    conclusion_corr_coef_sign = f"Так как a_calc = {a_corr_coef_calc} < a_level = {round(a_level, DecPlace)}" + \
        ", то гипотеза о равенстве нулю коэффициента линейной корреляции ОТВЕРГАЕТСЯ, т.е. линейная корреляционная связь ЗНАЧИМА"
print(conclusion_corr_coef_sign)

Теперь проверим значимость отличия линейной корреляционной связи от нелинейной. Для этого рассмотрим нулевую гипотезу:

H0: η² - r² = 0
H1: η² - r² ≠ 0

Для проверки нулевой гипотезы воспользуемся критерием Фишера:

print(f"Корреляционное отношение: {chr(951)} = {round(corr_ratio_XY, DecPlace)}")
print(f"Коэффициент линейной корреляции: r = {round(corr_coef, DecPlace)}")
# расчетное значение статистики критерия Фишера
F_line_corr_sign_calc = (n_X - K_X)/(K_X - 2) * (corr_ratio_XY**2 - corr_coef**2) / (1 - corr_ratio_XY**2)
print(f"Расчетное значение статистики критерия Фишера: F_calc = {round(F_line_corr_sign_calc, DecPlace)}")
# табличное значение статистики критерия Фишера
dfn = K_X - 2
dfd = n_X - K_X
F_line_corr_sign_table = sci.stats.f.ppf(p_level, dfn, dfd, loc=0, scale=1)
print(f"Табличное значение статистики критерия Фишера: F_table = {round(F_line_corr_sign_table, DecPlace)}")
# расчетный уровень значимости
a_line_corr_sign_calc = 1 - sci.stats.f.cdf(F_line_corr_sign_calc, dfn, dfd, loc=0, scale=1)
print(f"Расчетный уровень значимости: a_calc = {round(a_line_corr_sign_calc, DecPlace)}")
print(f"Заданный уровень значимости: a_level = {round(a_level, DecPlace)}")
# вывод
if F_line_corr_sign_calc < F_line_corr_sign_table:
    conclusion_line_corr_sign = f"Так как F_calc = {round(F_line_corr_sign_calc, DecPlace)} < F_table = {round(F_line_corr_sign_table, DecPlace)}" + \
        f", то гипотеза о равенстве {chr(951)} и r ПРИНИМАЕТСЯ, т.е. корреляционная связь ЛИНЕЙНАЯ"
else:
    conclusion_line_corr_sign = f"Так как F_calc = {round(F_line_corr_sign_calc, DecPlace)} >= F_table = {round(F_line_corr_sign_table, DecPlace)}" + \
        f", то гипотеза о равенстве {chr(951)} и r ОТВЕРГАЕТСЯ, т.е. корреляционная связь НЕЛИНЕЙНАЯ"
print(conclusion_line_corr_sign)

Создание пользовательской функции для корреляционного анализа

Для практической работы целесообразно все вышеприведенные расчеты реализовать в виде пользовательских функций:

• функция corr_coef_check - для расчета и анализа коэффициента линейной корреляции Пирсона

• функция corr_ratio_check - для расчета и анализа корреляционного отношения

• функция line_corr_sign_check - для проверка значимости линейной корреляционной связи

Данные функции выводят результаты анализа в виде DataFrame, что удобно для визуального восприятия и дальнейшего использования результатов анализа (впрочем, способ вывода - на усмотрение каждого исследователя).

# Функция для расчета и анализа коэффициента линейной корреляции Пирсона
def corr_coef_check(X, Y, p_level=0.95, scale='Cheddok'):
    a_level = 1 - p_level
    X = np.array(X)
    Y = np.array(Y)
    n_X = len(X)
    n_Y = len(Y)
    # оценка коэффициента линейной корреляции средствами scipy
    corr_coef, a_corr_coef_calc = sci.stats.pearsonr(X, Y)
    # несмещенная оценка коэффициента линейной корреляции (при n < 15) (см.Кобзарь, с.607)
    if n_X < 15:
        corr_coef = corr_coef * (1 + (1 - corr_coef**2) / (2*(n_X-3)))
    # проверка гипотезы о значимости коэффициента корреляции
    t_corr_coef_calc = abs(corr_coef) * sqrt(n_X-2) / sqrt(1 - corr_coef**2)
    t_corr_coef_table = sci.stats.t.ppf((1 + p_level)/2 , n_X - 2)
    conclusion_corr_coef_sign = 'significance' if t_corr_coef_calc >= t_corr_coef_table else 'not significance'
    # доверительный интервал коэффициента корреляции
    if t_corr_coef_calc >= t_corr_coef_table:
        z1 = np.arctanh(corr_coef) - sci.stats.norm.ppf((1 + p_level)/2, 0, 1) / sqrt(n_X-3) - corr_coef / (2*(n_X-1))
        z2 = np.arctanh(corr_coef) + sci.stats.norm.ppf((1 + p_level)/2, 0, 1) / sqrt(n_X-3) - corr_coef / (2*(n_X-1))
        corr_coef_conf_int_low = tanh(z1)
        corr_coef_conf_int_high = tanh(z2)
    else:
        corr_coef_conf_int_low = corr_coef_conf_int_high = '-'    
    # оценка тесноты связи
    if scale=='Cheddok':
        conclusion_corr_coef_scale = scale + ': ' + Cheddock_scale_check(corr_coef)
    elif scale=='Evans':
        conclusion_corr_coef_scale = scale + ': ' + Evans_scale_check(corr_coef)
    # формируем результат            
    result = pd.DataFrame({
        'notation': ('r'),
        'coef_value': (corr_coef),
        'coef_value_squared': (corr_coef**2),
        'p_level': (p_level),
        'a_level': (a_level),
        't_calc': (t_corr_coef_calc),
        't_table': (t_corr_coef_table),
        't_calc >= t_table': (t_corr_coef_calc >= t_corr_coef_table),
        'a_calc': (a_corr_coef_calc),
        'a_calc <= a_level': (a_corr_coef_calc <= a_level),
        'significance_check': (conclusion_corr_coef_sign),
        'conf_int_low': (corr_coef_conf_int_low),
        'conf_int_high': (corr_coef_conf_int_high),
        'scale': (conclusion_corr_coef_scale)
        },
        index=['Correlation coef.'])
        
    return result        

# Функция для расчета и анализа корреляционного отношения
def corr_ratio_check(X, Y, p_level=0.95, orientation='XY', scale='Cheddok'):
    a_level = 1 - p_level
    X = np.array(X)
    Y = np.array(Y)
    n_X = len(X)
    n_Y = len(Y)    
    # запишем данные в DataFrame
    matrix_XY_df = pd.DataFrame({
        'X': X,
        'Y': Y})
    # число интервалов группировки
    group_int_number = lambda n: round (3.31*log(n_X, 10)+1) if round (3.31*log(n_X, 10)+1) >=2 else 2
    K_X = group_int_number(n_X)
    K_Y = group_int_number(n_Y)
    # группировка данных и формирование корреляционной таблицы
    cut_X = pd.cut(X, bins=K_X)
    cut_Y = pd.cut(Y, bins=K_Y)
    matrix_XY_df['cut_X'] = cut_X
    matrix_XY_df['cut_Y'] = cut_Y
    CorrTable_df = pd.crosstab(
        index=matrix_XY_df['cut_X'],
        columns=matrix_XY_df['cut_Y'],
        rownames=['cut_X'],
        colnames=['cut_Y'])
    CorrTable_np = np.array(CorrTable_df)
    # итоги корреляционной таблицы по строкам и столбцам
    n_group_X = [np.sum(CorrTable_np[i]) for i in range(K_X)]
    n_group_Y = [np.sum(CorrTable_np[:,j]) for j in range(K_Y)]
    # среднегрупповые значения переменной X
    Xboun_mean = [(CorrTable_df.index[i].left + CorrTable_df.index[i].right)/2 for i in range(K_X)]
    Xboun_mean[0] = (np.min(X) + CorrTable_df.index[0].right)/2    # исправляем значения в крайних интервалах
    Xboun_mean[K_X-1] = (CorrTable_df.index[K_X-1].left + np.max(X))/2
    # среднегрупповые значения переменной Y
    Yboun_mean = [(CorrTable_df.columns[j].left + CorrTable_df.columns[j].right)/2 for j in range(K_Y)]
    Yboun_mean[0] = (np.min(Y) + CorrTable_df.columns[0].right)/2    # исправляем значения в крайних интервалах
    Yboun_mean[K_Y-1] = (CorrTable_df.columns[K_Y-1].left + np.max(Y))/2
    # средневзевешенные значения X и Y для каждой группы
    Xmean_group = [np.sum(CorrTable_np[:,j] * Xboun_mean) / n_group_Y[j] for j in range(K_Y)]
    Ymean_group = [np.sum(CorrTable_np[i] * Yboun_mean) / n_group_X[i] for i in range(K_X)]
    # общая дисперсия X и Y
    Sum2_total_X = np.sum(n_group_X * (Xboun_mean - np.mean(X))**2)
    Sum2_total_Y = np.sum(n_group_Y * (Yboun_mean - np.mean(Y))**2)
    # межгрупповая дисперсия X и Y (дисперсия групповых средних)
    Sum2_between_group_X = np.sum(n_group_Y * (Xmean_group - np.mean(X))**2)
    Sum2_between_group_Y = np.sum(n_group_X * (Ymean_group - np.mean(Y))**2)
    # эмпирическое корреляционное отношение
    corr_ratio_XY = sqrt(Sum2_between_group_Y / Sum2_total_Y)
    corr_ratio_YX = sqrt(Sum2_between_group_X / Sum2_total_X)
    try:
        if orientation!='XY' and orientation!='YX':
            raise ValueError("Error! Incorrect orientation!")
        if orientation=='XY':
            corr_ratio = corr_ratio_XY
        elif orientation=='YX':
            corr_ratio = corr_ratio_YX
    except ValueError as err:
        print(err)
    # проверка гипотезы о значимости корреляционного отношения
    F_corr_ratio_calc = (n_X - K_X)/(K_X - 1) * corr_ratio**2 / (1 - corr_ratio**2)
    dfn = K_X - 1
    dfd = n_X - K_X
    F_corr_ratio_table = sci.stats.f.ppf(p_level, dfn, dfd, loc=0, scale=1)
    a_corr_ratio_calc = 1 - sci.stats.f.cdf(F_corr_ratio_calc, dfn, dfd, loc=0, scale=1)
    conclusion_corr_ratio_sign = 'significance' if F_corr_ratio_calc >= F_corr_ratio_table else 'not significance'
    # доверительный интервал корреляционного отношения
    if F_corr_ratio_calc >= F_corr_ratio_table:
        f1 = round ((K_X - 1 + n_X * corr_ratio**2)**2 / (K_X - 1 + 2 * n_X * corr_ratio**2))
        f2 = n_X - K_X
        z1 = (n_X - K_X) / n_X * corr_ratio**2 / (1 - corr_ratio**2) * 1/sci.stats.f.ppf(p_level, f1, f2, loc=0, scale=1) - (K_X - 1)/n_X
        z2 = (n_X - K_X) / n_X * corr_ratio**2 / (1 - corr_ratio**2) * 1/sci.stats.f.ppf(1 - p_level, f1, f2, loc=0, scale=1) - (K_X - 1)/n_X
        corr_ratio_conf_int_low = sqrt(z1) if sqrt(z1) >= 0 else 0
        corr_ratio_conf_int_high = sqrt(z2) if sqrt(z2) <= 1 else 1
    else:
        corr_ratio_conf_int_low = corr_ratio_conf_int_high = '-'    
    # оценка тесноты связи
    if scale=='Cheddok':
        conclusion_corr_ratio_scale = scale + ': ' + Cheddock_scale_check(corr_ratio, name=chr(951))
    elif scale=='Evans':
        conclusion_corr_ratio_scale = scale + ': ' + Evans_scale_check(corr_ratio, name=chr(951))
    # формируем результат            
    result = pd.DataFrame({
        'notation': (chr(951)),
        'coef_value': (corr_ratio),
        'coef_value_squared': (corr_ratio**2),
        'p_level': (p_level),
        'a_level': (a_level),
        'F_calc': (F_corr_ratio_calc),
        'F_table': (F_corr_ratio_table),
        'F_calc >= F_table': (F_corr_ratio_calc >= F_corr_ratio_table),
        'a_calc': (a_corr_ratio_calc),
        'a_calc <= a_level': (a_corr_ratio_calc <= a_level),
        'significance_check': (conclusion_corr_ratio_sign),
        'conf_int_low': (corr_ratio_conf_int_low),
        'conf_int_high': (corr_ratio_conf_int_high),
        'scale': (conclusion_corr_ratio_scale)
        },
        index=['Correlation ratio'])
    
    return result        

# Функция для проверка значимости линейной корреляционной связи
def line_corr_sign_check(X, Y, p_level=0.95, orientation='XY'):
    a_level = 1 - p_level
    X = np.array(X)
    Y = np.array(Y)
    n_X = len(X)
    n_Y = len(Y)    
    # коэффициент корреляции
    corr_coef = sci.stats.pearsonr(X, Y)[0]
    # корреляционное отношение
    try:
        if orientation!='XY' and orientation!='YX':
            raise ValueError("Error! Incorrect orientation!")
        if orientation=='XY':
            corr_ratio = corr_ratio_check(X, Y, orientation='XY', scale='Evans')['coef_value'].values[0]
        elif orientation=='YX':
            corr_ratio = corr_ratio_check(X, Y, orientation='YX', scale='Evans')['coef_value'].values[0]
    except ValueError as err:
        print(err)
    # число интервалов группировки
    group_int_number = lambda n: round (3.31*log(n_X, 10)+1) if round (3.31*log(n_X, 10)+1) >=2 else 2
    K_X = group_int_number(n_X)
    # проверка гипотезы о значимости линейной корреляционной связи
    if corr_ratio >= abs(corr_coef):
        F_line_corr_sign_calc = (n_X - K_X)/(K_X - 2) * (corr_ratio**2 - corr_coef**2) / (1 - corr_ratio**2)
        dfn = K_X - 2
        dfd = n_X - K_X
        F_line_corr_sign_table = sci.stats.f.ppf(p_level, dfn, dfd, loc=0, scale=1)
        comparison_F_calc_table = F_line_corr_sign_calc >= F_line_corr_sign_table
        a_line_corr_sign_calc = 1 - sci.stats.f.cdf(F_line_corr_sign_calc, dfn, dfd, loc=0, scale=1)
        comparison_a_calc_a_level = a_line_corr_sign_calc <= a_level
        conclusion_null_hypothesis_check = 'accepted' if F_line_corr_sign_calc < F_line_corr_sign_table else 'unaccepted'
        conclusion_line_corr_sign = 'linear' if conclusion_null_hypothesis_check == 'accepted' else 'non linear'
    else:
        F_line_corr_sign_calc = ''
        F_line_corr_sign_table = ''
        comparison_F_calc_table = ''
        a_line_corr_sign_calc = ''
        comparison_a_calc_a_level = ''
        conclusion_null_hypothesis_check = 'Attention! The correlation ratio is less than the correlation coefficient'
        conclusion_line_corr_sign = '-'
    
    # формируем результат            
    result = pd.DataFrame({
        'corr.coef.': (corr_coef),
        'corr.ratio.': (corr_ratio),
        'null hypothesis': ('r\u00b2 = ' + chr(951) + '\u00b2'),
        'p_level': (p_level),
        'a_level': (a_level),
        'F_calc': (F_line_corr_sign_calc),
        'F_table': (F_line_corr_sign_table),
        'F_calc >= F_table': (comparison_F_calc_table),
        'a_calc': (a_line_corr_sign_calc),
        'a_calc <= a_level': (comparison_a_calc_a_level),
        'null_hypothesis_check': (conclusion_null_hypothesis_check),
        'significance_line_corr_check': (conclusion_line_corr_sign),
        },
        index=['Significance of linear correlation'])
    
    return result

display(corr_coef_check(X, Y, scale='Evans'))
display(corr_ratio_check(X, Y, orientation='XY', scale='Evans'))
display(line_corr_sign_check(X, Y, orientation='XY'))

Сделаем выводы по результатам расчетов:

1. Между величинами существует значимая (a_calc<0.05) корреляционная связь, корреляционное отношение η = 0.7936 (т.е. связь сильная по Эвансу).

2. Линейная корреляционная связь между величинами также значимая (a_calc<0.05), отрицательная, коэффициент корреляции r = -0.7189 (связь сильная по Эвансу); линейная корреляция между переменными объясняет 51.68% вариации.

3. Гипотеза о равенстве корреляционного отношения и коэффициента корреляции отвергается (a_calc<0.05), то есть отличие линейной формы связи от нелинейной значимо.

ИТОГИ

Итак, мы рассмотрели способы построения корреляционной таблицы, расчета корреляционного отношения, проверки его значимости и построения для него доверительных интервалов средствами Python. Также предложены пользовательские функции, уменьшающие размер кода.

Исходный код находится в моем репозитории на GitHub (https://github.com/AANazarov/Statistical-methods).

ЛИТЕРАТУРА

1. Айвазян С.А. и др. Прикладная статистика: исследование зависимостей. - М.: Финансы и статистика, 1985. - 487 с.

2. Айвазян С.А., Мхитарян В.С. Прикладная статистика. Основы эконометрики: В 2 т. - Т.1: Теория вероятностей и прикладная статистика. - М.: ЮНИТИ-ДАНА, 2001. - 656 с.

3. Кобзарь А.И. Прикладная математическая статистика. Для инженеров и научных работников. - М.: ФИЗМАТЛИТ, 2006. - 816 с.

4. Котеров А.Н. и др. Сила связи. Сообщение 2. Градации величины корреляции. - Медицинская радиология и радиационная безопасность. 2019. Том 64. № 6. с.12–24 (https://medradiol.fmbafmbc.ru/journal_medradiol/abstracts/2019/6/12-24_Koterov_et_al.pdf).