13.04.2023 23:18
ANazarov 15 1500 Источник

АКТУАЛЬНОСТЬ ТЕМЫ

В предыдущих обзорах (https://habr.com/ru/articles/690414/, https://habr.com/ru/articles/695556/) мы рассматривали линейную регрессию. Пришло время переходить к нелинейным моделями. Однако, прежде чем рассматривать полноценный нелинейный регрессионный анализ, остановимся на аппроксимации зависимостей.

Про аппроксимацию написано так много, что, кажется, и добавить уже нечего. Однако, кое-что добавить попытаемся.

При выполнении анализа данных может возникнуть потребность оперативно построить аналитическую зависимость. Подчеркиваю - речь не идет о полноценном регрессионном анализе со всеми его этапами, проверкой гипотез и т.д., а только лишь о подборе уравнения и оценке ошибки аппроксимации. Например, мы хотим оценить характер зависимости между какими-либо показателями в датасете и принять решение о целесообразности более глубокого исследования. Подобный инструмент предоставляет нам тот же Excel - все мы помним, как добавить линию тренда на точечном графике:

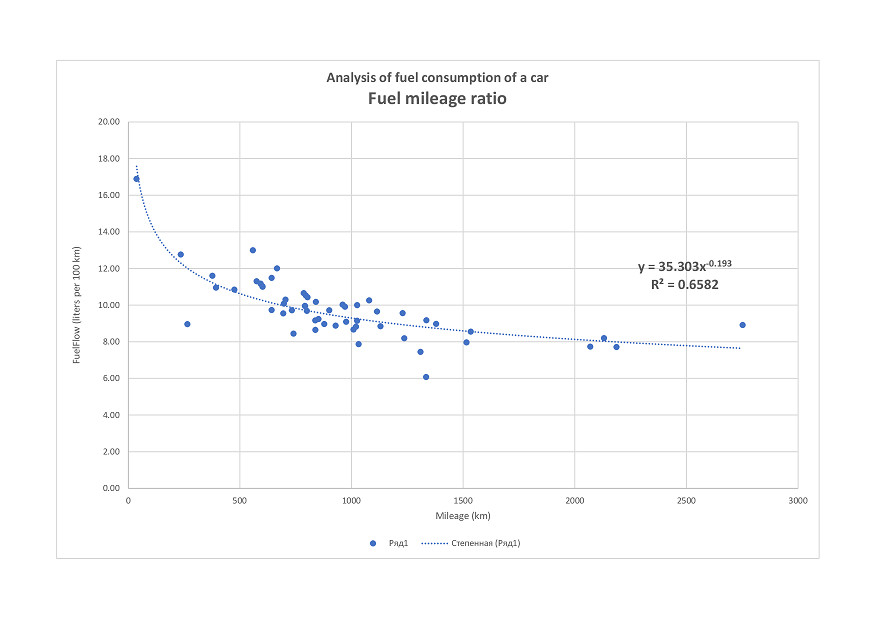
Такой же инструмент необходим и при работе в Python, причем желательно, сохранив главное достоинство - оперативность и удобство использования, избавиться от недостатков, присущих Excel:

  • ограниченный набор аналитических зависимостей и метрик качества аппроксимации;

  • невозможность построения нескольких зависимостей для одного набора данных;

  • невозможность установления ограничений на значения параметров зависимостей;

  • невозможность устранить влияние выбросов.

Использованием подобных инструментов мы и рассмотрим в данном обзоре.

Применение пользовательских функций

Как и в предыдущих обзорах, здесь будут использованы несколько пользовательских функций для решения разнообразных задач. Все эти функции созданы для облегчения работы и уменьшения размера программного кода. Данные функции загружается из пользовательского модуля my_module__stat.py, который доступен в моем репозитории на GitHub (https://github.com/AANazarov/MyModulePython).

Вот перечень данных функций:

  • graph_lineplot_sns - функция позволяет построить линейный график средствами seaborn и сохранить график в виде png-файла;

  • graph_scatterplot_sns - функция позволяет построить точечную диаграмму средствами seaborn и сохранить график в виде png-файла;

  • regression_error_metrics - функция возвращает ошибки аппроксимации регрессионной модели;

Пользовательскую функцию simple_approximation мы создаем в процессе данного обзора (она тоже включена в пользовательский модуль my_module__stat.py).

ИСХОДНЫЕ ДАННЫЕ

В качестве примера в данном обзоре продолжим рассматривать задачу нахождения зависимости среднемесячного расхода топлива автомобиля (л/100 км) (FuelFlow) от среднемесячного пробега (км) (Mileage) и среднемесячной температуры (Temperature) (этот же датасет я использовал в своих статьях: https://habr.com/ru/post/683442/, https://habr.com/ru/post/695556/).

# Общий заголовок проекта
Task_Project = "Analysis of fuel consumption of a car"

# Заголовок, фиксирующий момент времени
AsOfTheDate = ""

# Заголовок раздела проекта
Task_Theme = ""

# Общий заголовок проекта для графиков
Title_String = f"{Task_Project}\n{AsOfTheDate}"

# Наименования переменных
Variable_Name_T_month = "Monthly data"
Variable_Name_Y = "FuelFlow (liters per 100 km)"
Variable_Name_X1 = "Mileage (km)"
Variable_Name_X2 = "Temperature (°С)"

Загрузим исходные данные из csv-файла. Это уже обработанный датасет, готовый для анализа (первичная обработка данных выполненная в отдельном файле Preparation of input data.py, который также доступен в моем репозитории на GitHub).

Столбцы таблицы:

  • Month — месяц (в формате Excel)

  • Mileage - месячный пробег (км)

  • Temperature - среднемесячная температура (°C)

  • FuelFlow - среднемесячный расход топлива (л/100 к

dataset_df = pd.read_csv(filepath_or_buffer='data/dataset_df.csv', sep=';')

Сохранение данных

Сохраняем данные в виде отдельных переменных (для дальнейшего анализа).
Среднемесячный расход топлива (л/100 км) / Fuel Flow (liters per 100 km):

Y = np.array(dataset_df['Y'])

Пробег автомобиля за месяц (км) / Mileage (km):

X1 = np.array(dataset_df['X1'])

Среднемесячная температура (°С) / Temperature (degrees celsius):

X2 = np.array(dataset_df['X2'])

Визуализация

Границы значений переменных (при построении графиков):

(X1_min_graph, X1_max_graph) = (0, 3000)
(X2_min_graph, X2_max_graph) = (-20, 25)
(Y_min_graph, Y_max_graph) = (0, 30)

Построение графика:

graph_scatterplot_sns(
    X1, Y,
    Xmin=X1_min_graph, Xmax=X1_max_graph,
    Ymin=Y_min_graph, Ymax=Y_max_graph,
    color='orange',
    title_figure=Title_String, title_figure_fontsize=14,
    title_axes='Dependence of FuelFlow (Y) on mileage (X1)', title_axes_fontsize=16,
    x_label=Variable_Name_X1,
    y_label=Variable_Name_Y,
    label_fontsize=14, tick_fontsize=12,
    label_legend='', label_legend_fontsize=12,
    s=80)

ОСНОВЫ ТЕОРИИ

Кратко остановимся на некоторых теоретических вопросах.

Инструменты Python для аппроксимации

Python предоставляет нам большой набор инструментов для аппроксимации (подробнее см. https://docs.scipy.org/doc/scipy/reference/optimize.html). Мы остановимся на некоторых из них:

Основные виды моделей для аппроксимации

Не будем углубляться в классификацию моделей, об этом написаны сотни учебников, монографий, справочников и статей. Однако, в целях унификации в таблице ниже все-таки приведем основные виды моделей для аппроксимации - разумеется, это список не является исчерпывающим, но охватывает более или менее достаточный набор моделей для практического использования:

Наименование

Уравнение

линейная

Y=b_0+b_1\cdot X'

квадратическая

Y=b_0+b_1\cdot X+b_2\cdot X^2

кубическая

Y=b_0+b_1\cdot X+b_2\cdot X^2+b_3\cdot X^3

полиномиальная

Y=\sum b_k\cdot X^k

степенная

Y=b_0\cdot X^{b_1}

экспоненциальная I типа

Y=b_0\cdot e^{b_1\cdot X}

экспоненциальная II типа

Y=b_0\cdot b_1^X

логарифмическая

Y=b_0+b_1\cdot ln X

обратная логарифмическая

Y=1 / (b_0+b_1\cdot ln X)

гиперболическая I типа

Y=b_0+b_1 / X

гиперболическая II типа

Y=1 / (b_0+b_1\cdot X)

гиперболическая III типа

Y=X / (b_0+b_1\cdot X)

логистическая кривая I типа

Y=b_0 / (1+b_1\cdot e^{-b_2\cdot X})

логистическая кривая II типа (Перла-Рида)

Y=b_0 / (1+b_1\cdot b_2^{-X})

кривая Гомперца

Y=b_0\cdot {b_1}^{b_2^{X}}

модифицированная экспонента I типа

Y=b_0+b_1\cdot e^{b_2\cdot X}

модифицированная экспонента II типа

Y=b_0+b_1\cdot b_2^ X

обобщенная логистическая кривая I типа

Y=b_0+b_1 / (1+b_2\cdot e^{-b_3\cdot X})

обобщенная логистическая кривая II типа

Y=b_0+b_1 / (1+b_2\cdot b_3^{-X})

Примечания:

  1. Нелинейные модели в ряде источников принято делить на 2 группы:

    • модели, нелинейные по факторам - путем замены переменных могут быть линеаризованы, т.е. приведены к линейному виду, и для оценки их параметров может применяться классический метод наименьших квадратов;

    • модели, нелинейные по параметрам - не могут быть линеаризованы, и для оценки их параметров необходимо применять итерационные методы.

К моделям, нелинейным по параметрам, относятся, например, модифицированные кривые (модифицированная экспонента, обобщенная логистическая кривая), кривая Гомперца и пр. Оценка их параметров средствами Python требует особых приемов (предварительная оценка начальных значений). В данном разборе мы не будем особо останавливаться на этих моделях.

Оценка ошибок и доверительных интервалов для параметров моделей аппроксимации

  1. Экспоненциальные модели могут быть выражены в 2-х формах:

    • с помощью собственно экспоненциальной функции Y=b_0\cdot e^{b_1\cdot X};

    • в показательной форме Y=b_0\cdot b_1^X

  2. Не будем особо распространяться на опасности увлечения полиномиальными моделями для аппроксимации данных, отметим только, что использовать такие модели нужно очень осторожно, с особым обоснованием и содержательным анализом задачи, а полиномы выше 3-й степени вообще использовать не рекомендуется.

    Метрики качества аппроксимации

    Рассмотрим основные метрики качества:

    1. Mean squared error (MSE) - среднеквадратическая ошибка и Root mean square error (RMSE) - квадратный корень из среднеквадратической ошибки MSE:

    \begin{aligned} \qquad MSE = \frac{1}{n} \cdot {\displaystyle\sum_{i=1}^{n} (Y_{i} - \widehat{Y}_{i})^2} = \frac{1}{n} \cdot {\displaystyle\sum_{i=1}^{n} e_{i}^2} = \frac{1}{n} \cdot \boldsymbol{e}^T\boldsymbol{e} \end{aligned}

    \begin{aligned} \qquad RMSE = \sqrt{MSE} \end{aligned}

    Особенности: тенденция к занижение качества модели, чувствительность к выбросам.

    2. Mean absolute error (MAE) - средняя абсолютная ошибка:

    \begin{aligned} \qquad MAE = \frac{1}{n} \cdot {\displaystyle\sum_{i=1}^{n} |Y_{i} - \widehat{Y}_{i}|} \end{aligned}

    Особенность: гораздо менее чувствительна к выбросам, чем RMSE.

    3. Mean squared prediction error (MSPE) - среднеквадратическая ошибка прогноза (среднеквадратическая ошибка в процентах):

    \begin{aligned} \qquad MSPE = \frac{1}{n} \cdot {\displaystyle\sum_{i=1}^{n} \bigg(\frac{Y_{i} - \widehat{Y}_{i}}{Y_{i}}\bigg)^2} \end{aligned}

    Особенности: нечувствительность к выбросам; нельзя использовать для наблюдений, в которых значения выходной переменной равны нулю.

    4. Mean absolute percentage error (MAPE) - средняя абсолютная ошибка в процентах:

    \begin{aligned} \qquad MAPE = 1 - \frac{1}{n} \cdot {\displaystyle\sum_{i=1}^{n} \bigg|\frac{Y_{i} - \widehat{Y}_{i}}{Y_{i}}\bigg|} \end{aligned}

    Особенности: нельзя использовать для наблюдений, в которых значения выходной переменной равны нулю.

    5. Root Mean Square Logarithmic Error (RMSLE) - cреднеквадратичная логарифмическая ошибка, применяется, если разность между фактическим и предсказанным значениями различается на порядок и выше:

    \begin{aligned} \qquad RMSLE = \sqrt{\frac{1}{n} \cdot {\displaystyle\sum_{i=1}^{n} (ln(Y_i+1) - ln(\widehat{Y_{i}}+1))^2}} = RMSE\bigg(ln(Y), ln(\widehat{Y})\bigg) = \sqrt{MSE\bigg(ln(Y), ln(\widehat{Y})\bigg)} \end{aligned}

    Особенности: нечувствительность к выбросам; смещена в сторону меньших ошибок (наказывает больше на недооценку, чем за переоценку); к значениям добавляется константа 1, так как логарифм 0 не определен.

    6. \boldsymbol{R^2} - коэффициент детерминации:

    \begin{aligned} \qquad R^2 = 1 - \frac{SSE}{SST} = 1 - \frac{\displaystyle\sum_{i=1}^{n} (Y_{i} - \widehat{Y}_{i})^2}{\displaystyle\sum_{i=1}^{n} (Y_{i} - \overline{Y}_{i})^2} \end{aligned}

    Особенность: значение \boldsymbol{R^2} находится в пределах [0; 1], но иногда может принимать отрицательные значения (если ошибка модели больше ошибки среднего значения).
    Разумеется, приведенный перечень метрик качества аппроксимации не является исчерпывающим.

Сравнительный анализ метрик качества приведен в https://machinelearningmastery.ru/how-to-select-the-right-evaluation-metric-for-machine-learning-models-part-1-regrression-metrics-3606e25beae0/, https://machinelearningmastery.ru/how-to-select-the-right-evaluation-metric-for-machine-learning-models-part-2-regression-metrics-d4a1a9ba3d74/, https://loginom.ru/blog/quality-metrics.

Оценка ошибок и доверительных интервалов для параметров моделей аппроксимации

Инструменты аппроксимации Python позволяют получить довольно обширный набор различных данных, в том числе тех, которые нам дают возможность оценить ошибки параметров аппроксимации и построить для них доверительные интервалы. Не вдаваясь глубоко в математическую теорию вопроса, кратко разберем, как это реализовать на практике.

В общем виде доверительный интервал для параметров аппроксимации можно представить в виде p_j \pm \sigma_j, где p_j - значение j-го параметра модели, а \sigma_j - стандартная ошибка этого параметра.

Для определения \sigma_j нам необходима матрица ковариации оценок параметров \Sigma, диагональные элементы которой представляют собой дисперсию оценок параметров, то есть:

\begin{aligned} \qquad \sigma_j = \sqrt{\Sigma_{jj}}, \text{ } j=\overline{1,m} \end{aligned}

\Sigma имеет размерность [m \times m], где m - число оцениваемых параметров модели аппроксимации.

Теперь разберем, как получить \Sigma, используя различные инструменты аппроксимации Python:

  1. Функция scipy.optimize.curve_fit в стандартном наборе возвращаемых данных непосредственно содержит расчетную ковариационную матрицу \Sigma (The estimated covariance of popt), которая обозначается в программном коде как pcov (см. https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.curve_fit.html). Расчетная стандартная ошибка параметров может быть определена очень просто: perr = np.sqrt(np.diag(pcov)).

  2. Функция scipy.optimize.leastsq в стандартном наборе возвращаемых данных содержит матрицу, обратную матрице Гессе (The inverse of the Hessian) H^{-1}, которая обозначается в программном коде как cov_x. Чтобы получить \Sigma, необходимо умножить H^{-1} на величину остаточной дисперсии

    MSE = \frac{SSE}{df_E} = \frac{1}{n-m-1} \cdot \displaystyle\sum_{i=1}^{n} (y_i - \widehat{y}_i)^2:

    \begin{aligned} \Sigma = H^{-1} \cdot MSE \end{aligned}

    или в программном коде: pcov = cov_x*MSE.

    Величина SSE, необходимая для расчета MSE, может быть определена в программном коде как \mathsf{SSE = (infodict['fvec']**2).sum()}.

  3. Функция scipy.optimize.least_squares вместо H^{-1} возвращает модифицированную матрицу Якоби (Modified Jacobian matrix) J, которая обозначается в программном коде как result.jac (см. https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.least_squares.html#scipy.optimize.least_squares, https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.OptimizeResult.html#scipy.optimize.OptimizeResult). Получить H^{-1} можно следующим образом:

    \begin{aligned} H^{-1} = (J^T J)^{-1} \end{aligned}

    или в программном коде: cov_x = np.linalg.inv(np.dot(result.jac.T, result.jac)).

  4. Функция scipy.optimize.minimize имеет свои специфические особенности: возвращает обратную матрицу Гессе (Inverse of the objective function’s Hessian), которая обозначается в программном коде как res.hess_inv (см. https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html#scipy.optimize.minimize, https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.OptimizeResult.html#scipy.optimize.OptimizeResult), но для определения cov_x необходимо воспользоваться приближенным выражением cov_x = 2*res.hess_inv (подробнее об этом см. https://stackoverflow.com/questions/40187517/getting-covariance-matrix-of-fitted-parameters-from-scipy-optimize-least-squares).

  5. Библиотека lmfit позволяет непосредственно в стандартном наборе возвращаемых данных получить ошибки и доверительные интервалы параметров аппроксимации.

Более подробно с вопросом можно ознакомиться здесь:

АППРОКСИМАЦИЯ ЗАВИСИМОСТЕЙ

Определим набор зависимостей, которые будем использовать для аппроксимации. В данном обзоре мы рассмотрим набор наиболее широко распространенных зависимостей, не требующих особого подхода к вычислениям. Более сложные случаи - например, зависимости с асимптотами, зависимости нелинейные по параметрам и пр. - тема для отдельного рассмотрения.

# equations
linear_func = lambda x, b0, b1: b0 + b1*x
quadratic_func = lambda x, b0, b1, b2: b0 + b1*x + b2*x**2
qubic_func = lambda x, b0, b1, b2, b3: b0 + b1*x + b2*x**2 + b3*x**3
power_func = lambda x, b0, b1: b0 * (x**b1)
exponential_type_1_func = lambda x, b0, b1: b0*np.exp(b1*x)
exponential_type_2_func = lambda x, b0, b1: b0*np.power(b1, x)
logarithmic_func = lambda x, b0, b1: b0 + b1*np.log(x)
hyperbolic_func = lambda x, b0, b1: b0 + b1/x

Далее будем собственно выполнять аппроксимацию: оценивать параметры моделей, строить графики, причем так, чтобы на графиках отображались уравнения моделей и метрики качества (по аналогии с тем, как это позволяет сделать Excel - это очень удобно), рассмотрим возможность определения ошибок и доверительных интервалов для параметров аппроксимации.

Отдельно довольно кратко остановимся на библиотеке lmfit, которая предоставляет очень широкий инструментарий для аппроксимации.

Аппроксимация с использованием scipy.optimize.leastsq

Особенности использования функции:

  1. Реализация метода наименьших квадратов, без возможности введения ограничений на значения параметров.

  2. Возможность выбора метода оптимизации не предусмотрена.

Данный пакет считается устаревшим по сравнению, с least_squares.

Ссылка на документацию.

from scipy.optimize import leastsq

# list of model
model_list = [
    'linear', 'quadratic',
    'qubic', 'power',
    'exponential type 1', 'exponential type 2',
    'logarithmic',
    'hyperbolic']

# model reference
models_dict = {
        'linear':             linear_func,
        'quadratic':          quadratic_func,
        'qubic':              qubic_func,
        'power':              power_func,
        'exponential type 1': exponential_type_1_func,
        'exponential type 2': exponential_type_2_func,
        'logarithmic':        logarithmic_func,
        'hyperbolic':         hyperbolic_func}

# initial values
p0_dict = {
        'linear':             [0, 0],
        'quadratic':          [0, 0, 0],
        'qubic':              [0, 0, 0, 0],
        'power':              [0, 0],
        'exponential type 1': [0, 0],
        'exponential type 2': [1, 1],
        'logarithmic':        [0, 0],
        'hyperbolic':         [0, 0]}

# titles (formulas)
formulas_dict = {
        'linear':             'y = b0 + b1*x',
        'quadratic':          'y = b0 + b1*x + b2*x^2',
        'qubic':              'y = b0 + b1*x + b2*x^2 + b3*x^3',
        'power':              'y = b0*x^b1',
        'exponential type 1': 'y = b0*exp(b1^x)',
        'exponential type 2': 'y = b0*b1^x',
        'logarithmic':        'y = b0 + b1*ln(x)',
        'hyperbolic':         'y = b0+b1/x'}

# actual data
X_fact = X1
Y_fact = Y

# function for calculating residuals
residual_func = lambda p, x, y: y - func(x, *p)

# return all optional outputs
full_output = True

# variables to save the calculation results
calculation_results_df = pd.DataFrame(columns=['func', 'p0', 'popt', 'cov_x', 'SSE', 'MSE', 'pcov', 'perr', 'Y_calc', 'error_metrics'])
error_metrics_results_df = pd.DataFrame(columns=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE', 'R2'])

# calculations
for func_name in model_list:
    print(f'{func_name.upper()} MODEL: {formulas_dict[func_name]}')
    func = models_dict[func_name]
    calculation_results_df.loc[func_name, 'func'] = func
    p0 = p0_dict[func_name]
    print(f'p0 = {p0}')
    calculation_results_df.loc[func_name, 'p0'] = p0
    if full_output:
        (popt, cov_x, infodict, mesg, ier) = leastsq(residual_func, p0, args=(X_fact, Y_fact), full_output=full_output)
        integer_flag = f'ier = {ier}, the solution was found' if ier<=4 else f'ier = {ier}, the solution was not found'
        print(integer_flag, '\n', mesg)
        calculation_results_df.loc[func_name, 'popt'] = popt
        print(f'parameters = {popt}')
        calculation_results_df.loc[func_name, 'cov_x'] = cov_x
        print(f'cov_x = \n{cov_x}')
        #SSE = (residual_func(popt, X_fact, Y_fact)**2).sum()
        SSE = (infodict['fvec']**2).sum()
        calculation_results_df.loc[func_name, 'SSE'] = SSE
        print(f'SSE = {SSE}')
        MSE = SSE / (len(Y_fact)-len(p0))
        calculation_results_df.loc[func_name, 'MSE'] = MSE
        print(f'MSE = {MSE}')
        pcov = cov_x * MSE
        calculation_results_df.loc[func_name, 'pcov'] = pcov
        print(f'pcov =\n {pcov}')
        perr = np.sqrt(np.diag(pcov))
        calculation_results_df.loc[func_name, 'perr'] = perr
        print(f'perr = {perr}\n') 
    else:
        popt = leastsq(residual_func, p0, args=(X_fact, Y_fact), full_output=full_output)
        calculation_results_df.loc[func_name, 'popt'] = popt
        print(f'parameters = {popt}\n')
    Y_calc = func(X_fact, *popt)
    calculation_results_df.loc[func_name, 'Y_calc'] = Y_calc
    (error_metrics_dict, error_metrics_df) = regression_error_metrics(Yfact=Y_fact, Ycalc=Y_calc, model_name=func_name)
    calculation_results_df.loc[func_name, 'error_metrics'] = error_metrics_dict.values()
    error_metrics_results_df = pd.concat([error_metrics_results_df, error_metrics_df])        
LINEAR MODEL: y = b0 + b1*x
p0 = [0, 0]
ier = 3, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000 and the relative error between two consecutive iterates is at 
  most 0.000000
parameters = [ 1.1850e+01 -2.1760e-03]
cov_x = 
[[ 8.7797e-02 -7.3041e-05]
 [-7.3041e-05  7.6636e-08]]
SSE = 84.42039151684142
MSE = 1.5928375757894608
pcov =
 [[ 1.3985e-01 -1.1634e-04]
 [-1.1634e-04  1.2207e-07]]
perr = [3.7396e-01 3.4938e-04]

QUADRATIC MODEL: y = b0 + b1*x + b2*x^2
p0 = [0, 0, 0]
ier = 1, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000
parameters = [ 1.4343e+01 -7.0471e-03  1.8760e-06]
cov_x = 
[[ 2.8731e-01 -4.6282e-04  1.5012e-07]
 [-4.6282e-04  8.3812e-07 -2.9328e-10]
 [ 1.5012e-07 -2.9328e-10  1.1295e-13]]
SSE = 53.26102533463595
MSE = 1.0242504872045375
pcov =
 [[ 2.9428e-01 -4.7404e-04  1.5376e-07]
 [-4.7404e-04  8.5844e-07 -3.0039e-10]
 [ 1.5376e-07 -3.0039e-10  1.1569e-13]]
perr = [5.4247e-01 9.2652e-04 3.4013e-07]

QUBIC MODEL: y = b0 + b1*x + b2*x^2 + b3*x^3
p0 = [0, 0, 0, 0]
ier = 1, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000
parameters = [ 1.4838e+01 -8.8040e-03  3.5207e-06 -4.1264e-10]
cov_x = 
[[ 5.7657e-01 -1.4894e-03  1.1111e-06 -2.4112e-10]
 [-1.4894e-03  4.4815e-06 -3.7039e-09  8.5573e-13]
 [ 1.1111e-06 -3.7039e-09  3.3058e-12 -8.0107e-16]
 [-2.4112e-10  8.5573e-13 -8.0107e-16  2.0099e-19]]
SSE = 52.41383349470524
MSE = 1.0277222253863771
pcov =
 [[ 5.9256e-01 -1.5307e-03  1.1419e-06 -2.4780e-10]
 [-1.5307e-03  4.6057e-06 -3.8066e-09  8.7945e-13]
 [ 1.1419e-06 -3.8066e-09  3.3974e-12 -8.2328e-16]
 [-2.4780e-10  8.7945e-13 -8.2328e-16  2.0656e-19]]
perr = [7.6978e-01 2.1461e-03 1.8432e-06 4.5449e-10]

POWER MODEL: y = b0*x^b1
p0 = [0, 0]
ier = 1, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000
parameters = [33.4033 -0.1841]
cov_x = 
[[ 1.2667e+01 -5.7225e-02]
 [-5.7225e-02  2.6284e-04]]
SSE = 49.87968652194349
MSE = 0.9411261607913867
pcov =
 [[ 1.1922e+01 -5.3856e-02]
 [-5.3856e-02  2.4737e-04]]
perr = [3.4528 0.0157]

EXPONENTIAL TYPE 1 MODEL: y = b0*exp(b1^x)
p0 = [0, 0]
ier = 1, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000
parameters = [ 1.2624e+01 -2.7834e-04]
cov_x = 
[[ 1.5566e-01 -1.1829e-05]
 [-1.1829e-05  1.1127e-09]]
SSE = 75.19491109027253
MSE = 1.4187719073636327
pcov =
 [[ 2.2085e-01 -1.6783e-05]
 [-1.6783e-05  1.5787e-09]]
perr = [4.6994e-01 3.9733e-05]

EXPONENTIAL TYPE 2 MODEL: y = b0*b1^x
p0 = [1, 1]
ier = 1, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000
parameters = [12.6242  0.9997]
cov_x = 
[[ 1.5566e-01 -1.1826e-05]
 [-1.1826e-05  1.1121e-09]]
SSE = 75.19491108954423
MSE = 1.4187719073498912
pcov =
 [[ 2.2085e-01 -1.6778e-05]
 [-1.6778e-05  1.5778e-09]]
perr = [4.6994e-01 3.9722e-05]

LOGARITHMIC MODEL: y = b0 + b1*ln(x)
p0 = [0, 0]
ier = 3, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000 and the relative error between two consecutive iterates is at 
  most 0.000000
parameters = [23.9866 -2.1170]
cov_x = 
[[ 2.1029 -0.3106]
 [-0.3106  0.0463]]
SSE = 49.34256729321431
MSE = 0.9309918357210247
pcov =
 [[ 1.9578 -0.2891]
 [-0.2891  0.0431]]
perr = [1.3992 0.2075]

HYPERBOLIC MODEL: y = b0+b1/x
p0 = [0, 0]
ier = 1, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000
parameters = [  9.2219 315.7336]
cov_x = 
[[ 2.2732e-02 -2.5920e+00]
 [-2.5920e+00  1.4765e+03]]
SSE = 78.69038671392151
MSE = 1.4847242776211607
pcov =
 [[ 3.3751e-02 -3.8485e+00]
 [-3.8485e+00  2.1922e+03]]
perr = [ 0.1837 46.8207]

Теперь сформируем отдельный DataFrame, в котором соберем все результаты аппроксимации - параметры моделей (b_0, b_1, b_2, b_3), метрики качества (MSE, RMSE, MAE, MSPE, MAPE, RMSLE, R^2) и начальные условия (p_0, p_1, p_2, p_3).

Для улучшения восприятия используем возможности Python по визуализации таблиц (https://pandas.pydata.org/pandas-docs/stable/user_guide/style.html):

  • заменим nan на "-";

  • значения параметров моделей, величина которых сравнима с установленным пределом точности отображения (DecPlace), выделим цветом (orange);

  • для параметра b_1 установим повышенную точность отображения, а для параметров b_2, b_3 установим экспоненциальный формат;

  • для метрик качества установим выделение цветом наилучшего (green) и наихудшего (red) результата.

При этом нужно обратить внимание на следующее - пользовательская функция regression_error_metrics возвращает результат как в виде DataFrame, так и в виде словаря (dict):

  • если мы используем данные в виде DataFrame, то необходимо откорректировать значения признаков MSPE и MAPE, так как пользовательская функция regression_error_metrics возвращает значения этих признаков в строковом формате (из-за знака '%') и при определении наилучшего и наихудшего результатов могут возникнуть ошибки (значение '10%' будет считаться лучшим результатом, чем '9%' из-за того, что первым символом является единица), поэтому следует удалить знак '%' и изменить тип данных на float;

  • если мы используем данные в виде словаря (dict), то подобная проблема не возникает.

result_df = pd.DataFrame(
                list(calculation_results_df.loc[:,'p0'].values),
                columns=['p0', 'p1', 'p2', 'p3'],
                index=model_list)

result_df = result_df.join(pd.DataFrame(
                                list(calculation_results_df.loc[:,'popt'].values),
                                columns=['b0', 'b1', 'b2', 'b3'],
                                index=model_list))

result_df = result_df.join(pd.DataFrame(
                                list(calculation_results_df.loc[:,'perr'].values),
                                columns=['std(b0)', 'std(b1)', 'std(b2)', 'std(b3)'],
                                index=model_list))

result_df = result_df.join(pd.DataFrame(
                                list(calculation_results_df.loc[:,'error_metrics'].values),
                                columns=['MSE', 'RMSE',	'MAE', 'MSPE', 'MAPE', 'RMSLE', 'R2'],
                                index=model_list))

display(result_df)

# settings for displaying the DataFrame: result_df
result_df_leastsq = result_df.copy()
'''for elem in ['MSPE', 'MAPE']:
    result_df_leastsq[elem] = result_df_leastsq[elem].apply(lambda s: float(s[:-1]))'''
print('scipy.optimize.leastsq:'.upper())
display(result_df_leastsq
        .style
            .format(
                precision=DecPlace, na_rep='-',
                formatter={
                    'b1': '{:.' + str(DecPlace + 3) + 'f}',
                    'b2': '{:.' + str(DecPlace) + 'e}',
                    'b3': '{:.' + str(DecPlace) + 'e}',
                    'std(b1)': '{:.' + str(DecPlace + 3) + 'f}',
                    'std(b2)': '{:.' + str(DecPlace) + 'e}',
                    'std(b3)': '{:.' + str(DecPlace) + 'e}'})
            .highlight_min(color='green', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE'])
            .highlight_max(color='red', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE'])
            .highlight_max(color='green', subset='R2')
            .highlight_min(color='red', subset='R2')
            .applymap(lambda x: 'color: orange;' if abs(x) <= 10**(-(DecPlace-1)) else None, subset=['b0', 'b1', 'b2', 'b3', 'std(b0)', 'std(b1)', 'std(b2)', 'std(b3)']))

Сформируем DataFrame, содержащий ошибки и доверительные интервалы параметров моделей аппроксимации:

result_df_with_perr = pd.DataFrame()

parameter_name_list = ['b0', 'b1', 'b2', 'b3']
result_df_with_perr[parameter_name_list] = result_df[parameter_name_list]

parameter_format_dict = {
    'b0': '{:.' + str(DecPlace) + 'f}',
    'b1': '{:.' + str(DecPlace + 3) + 'f}',
    'b2': '{:.' + str(DecPlace) + 'e}',
    'b3': '{:.' + str(DecPlace) + 'e}',
    'std(b1)': '{:.' + str(DecPlace + 3) + 'f}',
    'std(b2)': '{:.' + str(DecPlace) + 'e}',
    'std(b3)': '{:.' + str(DecPlace) + 'e}'}

for parameter in parameter_name_list:
    for model in result_df.index:
        if not result_df.isna().loc[model, parameter]:
            result_df_with_perr.loc[model, parameter] = \
                str(parameter_format_dict[parameter].format(result_df.loc[model, parameter])) + \
                    ' ' + u"\u00B1" + ' ' + \
                    str(parameter_format_dict[parameter].format(result_df.loc[model, 'std('+parameter+')']))
            relative_errors = abs(result_df.loc[model, 'std('+parameter+')'] / result_df.loc[model, parameter])
            result_df_with_perr.loc[model, 'error('+parameter+')'] = '{:.3%}'.format(relative_errors)

result_df_with_perr_leastsq = result_df_with_perr.copy()
print('scipy.optimize.leastsq:'.upper())
display(result_df_with_perr_leastsq)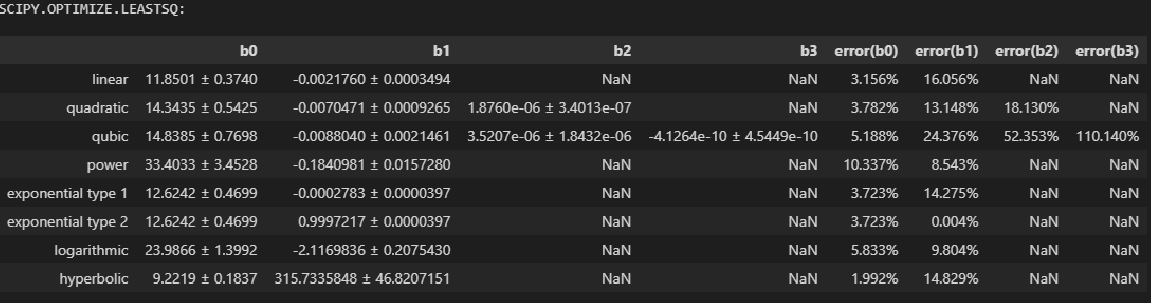
XY_calc_df = pd.DataFrame({
    'X_fact': X_fact,
    'Y_fact': Y_fact})
for i, model in enumerate(model_list):
    XY_calc_df[model] = calculation_results_df.loc[model, 'Y_calc']
display(XY_calc_df.head(), XY_calc_df.tail())

Построим графики аппроксимации (по аналогии с Excel):

# setting colors for graphs
color_dict = {
        'linear':                      'blue',
        'quadratic':                   'darkblue',
        'qubic':                       'slateblue',
        'power':                       'magenta',
        'exponential type 1':          'cyan',
        'exponential type 2':          'black',
        'logarithmic':                 'orange',
        'inverse logarithmic':         'gold',
        'hyperbolic':                  'grey',
        'hyperbolic type 2':           'darkgrey',
        'hyperbolic type 3':           'lightgrey',
        'modified exponential type 1': 'darkcyan',
        'modified exponential type 2': 'black',
        'logistic type 1':             'green',
        'logistic type 2':             'darkgreen',
        'Gompertz':                    'brown'
        }

linewidth_dict = {
        'linear':                      2,
        'quadratic':                   2,
        'qubic':                       2,
        'power':                       2,
        'exponential type 1':          5,
        'exponential type 2':          1,
        'logarithmic':                 2,
        'inverse logarithmic':         2,
        'hyperbolic':                  2,
        'hyperbolic type 2':           2,
        'hyperbolic type 3':           2,
        'modified exponential type 1': 2,
        'modified exponential type 2': 2,
        'logistic type 1':             2,
        'logistic type 2':             2,
        'Gompertz':                    2
        }

# changing the Matplotlib settings
plt.rcParams['axes.titlesize'] = 14
plt.rcParams['legend.fontsize'] = 12
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12

# bounds of values of variables (when plotting)
Xmin = X1_min_graph
Xmax = X1_max_graph
Ymin = Y_min_graph
Ymax = Y_max_graph

# the value of the independent variable (when plotting)
nx = 100
hx = (Xmax - Xmin)/(nx - 1)
X_calc_graph = np.linspace(Xmin, Xmax, nx)

# plotting
fig, axes = plt.subplots(figsize=(420/INCH, 297/INCH))
title_figure = Title_String + '\n' + Task_Theme + '\n'
fig.suptitle(title_figure, fontsize = 16)
title_axes = 'Fuel mileage ratio'
axes.set_title(title_axes, fontsize = 18)

# actual data
sns.scatterplot(
    x=X_fact, y=Y_fact,
    label='data',
    s=75,
    color='red',
    ax=axes)

# models
for func_name in model_list:
    R2 = round(result_df.loc[func_name,'R2'], DecPlace)
    RMSE = round(result_df.loc[func_name,'RMSE'], DecPlace)
    MAE = round(result_df.loc[func_name,'MAE'], DecPlace)
    MSPE = "{:.3%}".format(result_df.loc[func_name,'MSPE'])
    MAPE = "{:.3%}".format(result_df.loc[func_name,'MAPE'])
    label = func_name + ' '+ r'$(R^2 = $' + f'{R2}' + ', ' + f'RMSE = {RMSE}' + ', ' + f'MAE = {MAE}' + ', ' + f'MSPE = {MSPE}' + ', ' + f'MAPE = {MAPE})'
    func = calculation_results_df.loc[func_name, 'func']
    popt = calculation_results_df.loc[func_name, 'popt']
    sns.lineplot(
        x=X_calc_graph, y=func(X_calc_graph, *popt),
        color=color_dict[func_name],
        linewidth=linewidth_dict[func_name],
        legend=True,
        label=label,
        ax=axes)

axes.set_xlim(Xmin, Xmax)
axes.set_ylim(Ymin, Ymax)
axes.set_xlabel(Variable_Name_X1, fontsize = 14)
axes.set_ylabel(Variable_Name_Y, fontsize = 14)
axes.legend(prop={'size': 12})

plt.show()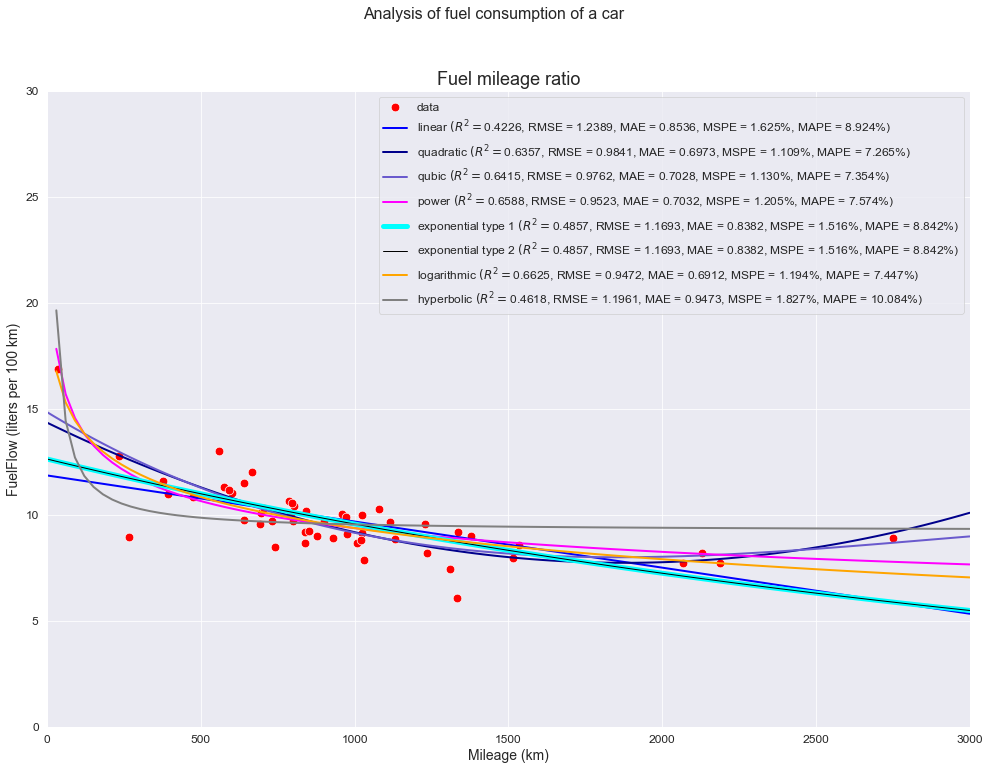

Аппроксимация с использованием scipy.optimize.least_squares

Особенности использования функции:

  1. Реализация нелинейного метода наименьших квадратов, с возможностью введения ограничений на значения параметров.

  2. Имеется возможность выбора алгоритма оптимизации:

    • trf (Trust Region Reflective) - установлен по умолчанию, надежный метод, особенно подходящий для больших задач с ограничениями;

    • dogbox - для небольших задач с ограничениями;

    • lm (Levenberg-Marquardt algorithm) - для небольших задач без ограничений.

Ссылка на документацию.

from scipy.optimize import least_squares

# algorithm to perform minimization
methods_dict = {
        'linear':             'lm',
        'quadratic':          'lm',
        'qubic':              'lm',
        'power':              'lm',
        'exponential type 1': 'lm',
        'exponential type 2': 'lm',
        'logarithmic':        'lm',
        'hyperbolic':         'lm'}

# actual data
X_fact = X1
Y_fact = Y

# function for calculating residuals
residual_func = lambda p, x, y: y - func(x, *p)

# return all optional outputs
full_output = True

# variables to save the calculation results
calculation_results_df = pd.DataFrame(columns=['func', 'p0', 'popt', 'jac', 'hess', 'SSE', 'MSE', 'pcov', 'perr', 'Y_calc', 'error_metrics'])
error_metrics_results_df = pd.DataFrame(columns=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE', 'R2'])

# calculations
for func_name in model_list:
    print(f'{func_name.upper()} MODEL: {formulas_dict[func_name]}')
    func = models_dict[func_name]
    calculation_results_df.loc[func_name, 'func'] = func
    p0 = p0_dict[func_name]
    print(f'p0 = {p0}')
    calculation_results_df.loc[func_name, 'p0'] = p0
    res = sci.optimize.least_squares(residual_func, p0, args=(X_fact, Y_fact), method=methods_dict[func_name])
    (popt, jac) = (res.x, res.jac)
    calculation_results_df.loc[func_name, 'popt'] = popt
    calculation_results_df.loc[func_name, 'jac'] = jac
    print(f'parameters = {popt}')
    #print(f'jac =\n {jac}')
    hess = np.linalg.inv(np.dot(jac.T, jac))
    calculation_results_df.loc[func_name, 'hess'] = hess
    print(f'hess =\n {hess}')
    SSE = (residual_func(popt, X_fact, Y_fact)**2).sum()
    calculation_results_df.loc[func_name, 'SSE'] = SSE
    print(f'SSE = {SSE}')
    MSE = SSE / (len(Y_fact)-len(p0))
    calculation_results_df.loc[func_name, 'MSE'] = MSE
    print(f'MSE = {MSE}')
    pcov = hess * MSE
    calculation_results_df.loc[func_name, 'pcov'] = pcov
    print(f'pcov =\n {pcov}')
    perr = np.sqrt(np.diag(pcov))
    calculation_results_df.loc[func_name, 'perr'] = perr
    print(f'perr = {perr}\n')
    Y_calc = func(X_fact, *popt)
    calculation_results_df.loc[func_name, 'Y_calc'] = Y_calc
    (error_metrics_dict, error_metrics_df) = regression_error_metrics(Yfact=Y_fact, Ycalc=Y_calc, model_name=func_name)
    calculation_results_df.loc[func_name, 'error_metrics'] = error_metrics_dict.values()
    error_metrics_results_df = pd.concat([error_metrics_results_df, error_metrics_df])
LINEAR MODEL: y = b0 + b1*x
p0 = [0, 0]
parameters = [ 1.1850e+01 -2.1760e-03]
hess =
 [[ 8.7797e-02 -7.3041e-05]
 [-7.3041e-05  7.6636e-08]]
SSE = 84.42039151684142
MSE = 1.5928375757894608
pcov =
 [[ 1.3985e-01 -1.1634e-04]
 [-1.1634e-04  1.2207e-07]]
perr = [3.7396e-01 3.4938e-04]

QUADRATIC MODEL: y = b0 + b1*x + b2*x^2
p0 = [0, 0, 0]
parameters = [ 1.4343e+01 -7.0471e-03  1.8760e-06]
hess =
 [[ 2.8731e-01 -4.6282e-04  1.5012e-07]
 [-4.6282e-04  8.3812e-07 -2.9328e-10]
 [ 1.5012e-07 -2.9328e-10  1.1295e-13]]
SSE = 53.26102533463595
MSE = 1.0242504872045375
pcov =
 [[ 2.9428e-01 -4.7404e-04  1.5376e-07]
 [-4.7404e-04  8.5844e-07 -3.0039e-10]
 [ 1.5376e-07 -3.0039e-10  1.1569e-13]]
perr = [5.4247e-01 9.2652e-04 3.4013e-07]

QUBIC MODEL: y = b0 + b1*x + b2*x^2 + b3*x^3
p0 = [0, 0, 0, 0]
parameters = [ 1.4838e+01 -8.8040e-03  3.5207e-06 -4.1264e-10]
hess =
 [[ 5.7657e-01 -1.4894e-03  1.1111e-06 -2.4112e-10]
 [-1.4894e-03  4.4815e-06 -3.7039e-09  8.5573e-13]
 [ 1.1111e-06 -3.7039e-09  3.3058e-12 -8.0107e-16]
 [-2.4112e-10  8.5573e-13 -8.0107e-16  2.0099e-19]]
SSE = 52.413833494705216
MSE = 1.0277222253863767
pcov =
 [[ 5.9256e-01 -1.5307e-03  1.1419e-06 -2.4780e-10]
 [-1.5307e-03  4.6057e-06 -3.8066e-09  8.7945e-13]
 [ 1.1419e-06 -3.8066e-09  3.3974e-12 -8.2328e-16]
 [-2.4780e-10  8.7945e-13 -8.2328e-16  2.0656e-19]]
perr = [7.6978e-01 2.1461e-03 1.8432e-06 4.5449e-10]

POWER MODEL: y = b0*x^b1
p0 = [0, 0]
parameters = [33.4033 -0.1841]
hess =
 [[ 1.2667e+01 -5.7226e-02]
 [-5.7226e-02  2.6284e-04]]
SSE = 49.87968652202211
MSE = 0.94112616079287
pcov =
 [[ 1.1922e+01 -5.3857e-02]
 [-5.3857e-02  2.4737e-04]]
perr = [3.4528 0.0157]

EXPONENTIAL TYPE 1 MODEL: y = b0*exp(b1^x)
p0 = [0, 0]
parameters = [ 1.2624e+01 -2.7834e-04]
hess =
 [[ 1.5566e-01 -1.1829e-05]
 [-1.1829e-05  1.1127e-09]]
SSE = 75.19491109027253
MSE = 1.4187719073636327
pcov =
 [[ 2.2085e-01 -1.6782e-05]
 [-1.6782e-05  1.5787e-09]]
perr = [4.6994e-01 3.9732e-05]

EXPONENTIAL TYPE 2 MODEL: y = b0*b1^x
p0 = [1, 1]
parameters = [12.6242  0.9997]
hess =
 [[ 1.5566e-01 -1.1825e-05]
 [-1.1825e-05  1.1121e-09]]
SSE = 75.19491108936178
MSE = 1.4187719073464486
pcov =
 [[ 2.2085e-01 -1.6778e-05]
 [-1.6778e-05  1.5778e-09]]
perr = [4.6994e-01 3.9721e-05]

LOGARITHMIC MODEL: y = b0 + b1*ln(x)
p0 = [0, 0]
parameters = [23.9866 -2.1170]
hess =
 [[ 2.1029 -0.3106]
 [-0.3106  0.0463]]
SSE = 49.342567293214316
MSE = 0.9309918357210248
pcov =
 [[ 1.9578 -0.2891]
 [-0.2891  0.0431]]
perr = [1.3992 0.2075]

HYPERBOLIC MODEL: y = b0+b1/x
p0 = [0, 0]
parameters = [  9.2219 315.7336]
hess =
 [[ 2.2732e-02 -2.5920e+00]
 [-2.5920e+00  1.4765e+03]]
SSE = 78.69038671392154
MSE = 1.484724277621161
pcov =
 [[ 3.3751e-02 -3.8485e+00]
 [-3.8485e+00  2.1922e+03]]
perr = [ 0.1837 46.8207]

По аналогии с предыдущим примером, сформируем отдельный DataFrame, в котором соберем все результаты аппроксимации, и сравним с результатами из предыдущего примера:

result_df = pd.DataFrame(
                list(calculation_results_df.loc[:,'p0'].values),
                columns=['p0', 'p1', 'p2', 'p3'],
                index=model_list)

result_df = result_df.join(pd.DataFrame(
                                list(calculation_results_df.loc[:,'popt'].values),
                                columns=['b0', 'b1', 'b2', 'b3'],
                                index=model_list))

result_df = result_df.join(pd.DataFrame(
                                list(calculation_results_df.loc[:,'perr'].values),
                                columns=['std(b0)', 'std(b1)', 'std(b2)', 'std(b3)'],
                                index=model_list))

result_df = result_df.join(pd.DataFrame(
                                list(calculation_results_df.loc[:,'error_metrics'].values),
                                columns=['MSE', 'RMSE',	'MAE', 'MSPE', 'MAPE', 'RMSLE', 'R2'],
                                index=model_list))

#display(result_df)

# settings for displaying the DataFrame: result_df
result_df_least_squares = result_df.copy()
'''for elem in ['MSPE', 'MAPE']:
    result_df_leastsq[elem] = result_df_leastsq[elem].apply(lambda s: float(s[:-1]))'''
print('scipy.optimize.least_squares:'.upper())
display(result_df_least_squares
        .style
            .format(
                precision=DecPlace, na_rep='-',
                formatter={
                    'b1': '{:.' + str(DecPlace + 3) + 'f}',
                    'b2': '{:.' + str(DecPlace) + 'e}',
                    'b3': '{:.' + str(DecPlace) + 'e}',
                    'std(b1)': '{:.' + str(DecPlace + 3) + 'f}',
                    'std(b2)': '{:.' + str(DecPlace) + 'e}',
                    'std(b3)': '{:.' + str(DecPlace) + 'e}'})
            .highlight_min(color='green', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE'])
            .highlight_max(color='red', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE'])
            .highlight_max(color='green', subset='R2')
            .highlight_min(color='red', subset='R2')
            .applymap(lambda x: 'color: orange;' if abs(x) <= 10**(-(DecPlace-1)) else None, subset=['b0', 'b1', 'b2', 'b3', 'std(b0)', 'std(b1)', 'std(b2)', 'std(b3)']))    

print('scipy.optimize.leastsq:'.upper())
display(result_df_leastsq
        .style
            .format(
                precision=DecPlace, na_rep='-',
                formatter={
                    'b1': '{:.' + str(DecPlace + 3) + 'f}',
                    'b2': '{:.' + str(DecPlace) + 'e}',
                    'b3': '{:.' + str(DecPlace) + 'e}',
                    'std(b1)': '{:.' + str(DecPlace + 3) + 'f}',
                    'std(b2)': '{:.' + str(DecPlace) + 'e}',
                    'std(b3)': '{:.' + str(DecPlace) + 'e}'})
            .highlight_min(color='green', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE'])
            .highlight_max(color='red', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE'])
            .highlight_max(color='green', subset='R2')
            .highlight_min(color='red', subset='R2')
            .applymap(lambda x: 'color: orange;' if abs(x) <= 10**(-(DecPlace-1)) else None, subset=['b0', 'b1', 'b2', 'b3', 'std(b0)', 'std(b1)', 'std(b2)', 'std(b3)']))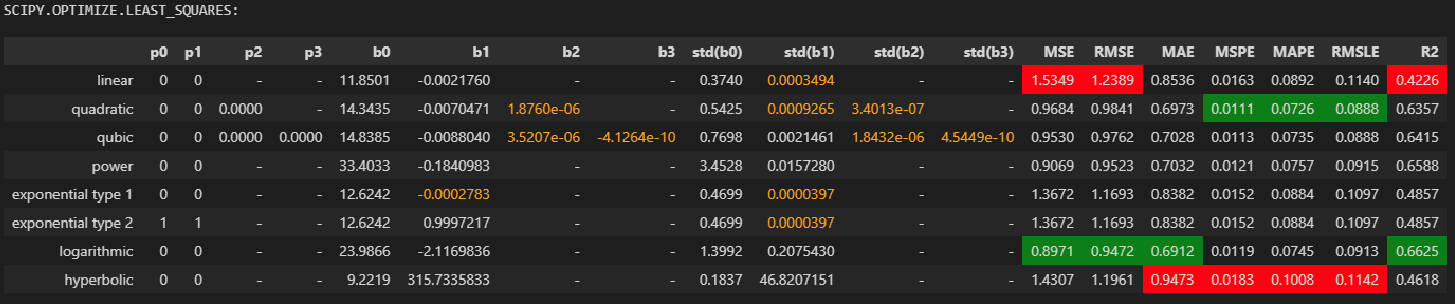

Сформируем DataFrame, содержащий ошибки и доверительные интервалы параметров моделей аппроксимации, и сравним с результатами из предыдущего примера:

result_df_with_perr = pd.DataFrame()

parameter_name_list = ['b0', 'b1', 'b2', 'b3']
result_df_with_perr[parameter_name_list] = result_df[parameter_name_list]

parameter_format_dict = {
    'b0': '{:.' + str(DecPlace) + 'f}',
    'b1': '{:.' + str(DecPlace + 3) + 'f}',
    'b2': '{:.' + str(DecPlace) + 'e}',
    'b3': '{:.' + str(DecPlace) + 'e}',
    'std(b1)': '{:.' + str(DecPlace + 3) + 'f}',
    'std(b2)': '{:.' + str(DecPlace) + 'e}',
    'std(b3)': '{:.' + str(DecPlace) + 'e}'}

for parameter in parameter_name_list:
    for model in result_df.index:
        if not result_df.isna().loc[model, parameter]:
            result_df_with_perr.loc[model, parameter] = \
                str(parameter_format_dict[parameter].format(result_df.loc[model, parameter])) + \
                    ' ' + u"\u00B1" + ' ' + \
                    str(parameter_format_dict[parameter].format(result_df.loc[model, 'std('+parameter+')']))
            relative_errors = abs(result_df.loc[model, 'std('+parameter+')'] / result_df.loc[model, parameter])
            result_df_with_perr.loc[model, 'error('+parameter+')'] = '{:.3%}'.format(relative_errors)

result_df_with_perr_least_squares = result_df_with_perr.copy()
print('scipy.optimize.least_squares:'.upper())
display(result_df_with_perr_least_squares)

print('scipy.optimize.leastsq:'.upper())
display(result_df_with_perr_leastsq)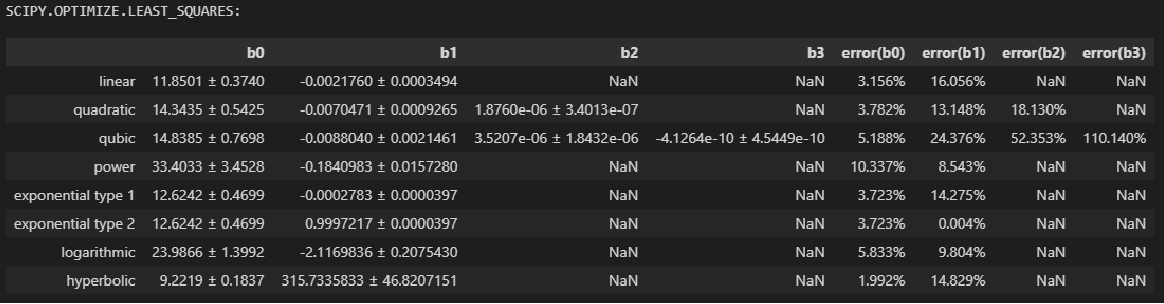

Аппроксимация с использованием scipy.optimize.curve_fit

Особенности использования функции:

  1. Реализация нелинейного метода наименьших квадратов, с возможностью введения ограничений на значения параметров.

  2. Имеется возможность выбора алгоритма оптимизации (trf, dogbox, lm), по аналогии с scipy.optimize.least_squares).

Ссылка на документацию.

from scipy.optimize import curve_fit

# algorithm to perform minimization
methods_dict = {
        'linear':             'lm',
        'quadratic':          'lm',
        'qubic':              'lm',
        'power':              'lm',
        'exponential type 1': 'lm',
        'exponential type 2': 'lm',
        'logarithmic':        'lm',
        'hyperbolic':         'lm'}

# actual data
X_fact = X1
Y_fact = Y

# return all optional outputs
full_output = True

# variables to save the calculation results
calculation_results_df = pd.DataFrame(columns=['func', 'p0', 'popt', 'pcov', 'perr', 'Y_calc', 'error_metrics'])
error_metrics_results_df = pd.DataFrame(columns=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE', 'R2'])

# calculations
for func_name in model_list:
    print(f'{func_name.upper()} MODEL: {formulas_dict[func_name]}')
    func = models_dict[func_name]
    calculation_results_df.loc[func_name, 'func'] = func
    p0 = p0_dict[func_name]
    print(f'p0 = {p0}')
    calculation_results_df.loc[func_name, 'p0'] = p0
    if full_output:
        (popt, pcov, infodict, mesg, ier) = curve_fit(func, X_fact, Y_fact, p0=p0, method=methods_dict[func_name], full_output=full_output)
        integer_flag = f'ier = {ier}, the solution was found' if ier<=4 else f'ier = {ier}, the solution was not found'
        print(integer_flag, '\n', mesg)
        calculation_results_df.loc[func_name, 'popt'] = popt
        print(f'parameters = {popt}')
        calculation_results_df.loc[func_name, 'pcov'] = pcov
        print(f'pcov =\n {pcov}')
        perr = np.sqrt(np.diag(pcov))
        calculation_results_df.loc[func_name, 'perr'] = perr
        print(f'perr = {perr}\n') 
    else:
        (popt, pcov) = curve_fit(func, X_fact, Y_fact, p0=p0, method=methods_dict[func_name], full_output=full_output)
        calculation_results_df.loc[func_name, 'popt'] = popt
        print(f'parameters = {popt}')
        calculation_results_df.loc[func_name, 'pcov'] = pcov
        print(f'pcov =\n {pcov}')
        perr = np.sqrt(np.diag(pcov))
        calculation_results_df.loc[func_name, 'perr'] = perr
        print(f'perr = {perr}\n') 
    Y_calc = func(X_fact, *popt)
    calculation_results_df.loc[func_name, 'Y_calc'] = Y_calc
    (error_metrics_dict, error_metrics_df) = regression_error_metrics(Yfact=Y_fact, Ycalc=Y_calc, model_name=func_name)
    calculation_results_df.loc[func_name, 'error_metrics'] = error_metrics_dict.values()
    error_metrics_results_df = pd.concat([error_metrics_results_df, error_metrics_df])        
LINEAR MODEL: y = b0 + b1*x
p0 = [0, 0]
ier = 3, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000 and the relative error between two consecutive iterates is at 
  most 0.000000
parameters = [ 1.1850e+01 -2.1760e-03]
pcov =
 [[ 1.3985e-01 -1.1634e-04]
 [-1.1634e-04  1.2207e-07]]
perr = [3.7396e-01 3.4938e-04]

QUADRATIC MODEL: y = b0 + b1*x + b2*x^2
p0 = [0, 0, 0]
ier = 1, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000
parameters = [ 1.4343e+01 -7.0471e-03  1.8760e-06]
pcov =
 [[ 2.9428e-01 -4.7404e-04  1.5376e-07]
 [-4.7404e-04  8.5844e-07 -3.0039e-10]
 [ 1.5376e-07 -3.0039e-10  1.1569e-13]]
perr = [5.4247e-01 9.2652e-04 3.4013e-07]

QUBIC MODEL: y = b0 + b1*x + b2*x^2 + b3*x^3
p0 = [0, 0, 0, 0]
ier = 1, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000
parameters = [ 1.4838e+01 -8.8040e-03  3.5207e-06 -4.1264e-10]
pcov =
 [[ 5.9256e-01 -1.5307e-03  1.1419e-06 -2.4780e-10]
 [-1.5307e-03  4.6057e-06 -3.8066e-09  8.7945e-13]
 [ 1.1419e-06 -3.8066e-09  3.3974e-12 -8.2328e-16]
 [-2.4780e-10  8.7945e-13 -8.2328e-16  2.0656e-19]]
perr = [7.6978e-01 2.1461e-03 1.8432e-06 4.5449e-10]

POWER MODEL: y = b0*x^b1
p0 = [0, 0]
ier = 1, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000
parameters = [33.4033 -0.1841]
pcov =
 [[ 1.1922e+01 -5.3856e-02]
 [-5.3856e-02  2.4737e-04]]
perr = [3.4528 0.0157]

EXPONENTIAL TYPE 1 MODEL: y = b0*exp(b1^x)
p0 = [0, 0]
ier = 1, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000
parameters = [ 1.2624e+01 -2.7834e-04]
pcov =
 [[ 2.2085e-01 -1.6783e-05]
 [-1.6783e-05  1.5787e-09]]
perr = [4.6994e-01 3.9733e-05]

EXPONENTIAL TYPE 2 MODEL: y = b0*b1^x
p0 = [1, 1]
ier = 1, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000
parameters = [12.6242  0.9997]
pcov =
 [[ 2.2085e-01 -1.6778e-05]
 [-1.6778e-05  1.5778e-09]]
perr = [4.6994e-01 3.9722e-05]

LOGARITHMIC MODEL: y = b0 + b1*ln(x)
p0 = [0, 0]
ier = 3, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000 and the relative error between two consecutive iterates is at 
  most 0.000000
parameters = [23.9866 -2.1170]
pcov =
 [[ 1.9578 -0.2891]
 [-0.2891  0.0431]]
perr = [1.3992 0.2075]

HYPERBOLIC MODEL: y = b0+b1/x
p0 = [0, 0]
ier = 1, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000
parameters = [  9.2219 315.7336]
pcov =
 [[ 3.3751e-02 -3.8485e+00]
 [-3.8485e+00  2.1922e+03]]
perr = [ 0.1837 46.8207]

По аналогии с предыдущим примером, сформируем отдельный DataFrame, в котором соберем все результаты аппроксимации, и сравним с результатами из предыдущих примеров:

result_df = pd.DataFrame(
                list(calculation_results_df.loc[:,'p0'].values),
                columns=['p0', 'p1', 'p2', 'p3'],
                index=model_list)

result_df = result_df.join(pd.DataFrame(
                                list(calculation_results_df.loc[:,'popt'].values),
                                columns=['b0', 'b1', 'b2', 'b3'],
                                index=model_list))

result_df = result_df.join(pd.DataFrame(
                                list(calculation_results_df.loc[:,'perr'].values),
                                columns=['std(b0)', 'std(b1)', 'std(b2)', 'std(b3)'],
                                index=model_list))

result_df = result_df.join(pd.DataFrame(
                                list(calculation_results_df.loc[:,'error_metrics'].values),
                                columns=['MSE', 'RMSE',	'MAE', 'MSPE', 'MAPE', 'RMSLE', 'R2'],
                                index=model_list))

#display(result_df)

# settings for displaying the DataFrame: result_df
result_df_curve_fit = result_df.copy()
'''for elem in ['MSPE', 'MAPE']:
    result_df_leastsq[elem] = result_df_leastsq[elem].apply(lambda s: float(s[:-1]))'''
print('scipy.optimize.curve_fit:'.upper())
display(result_df_curve_fit
        .style
            .format(
                precision=DecPlace, na_rep='-',
                formatter={
                    'b1': '{:.' + str(DecPlace + 3) + 'f}',
                    'b2': '{:.' + str(DecPlace) + 'e}',
                    'b3': '{:.' + str(DecPlace) + 'e}',
                    'std(b1)': '{:.' + str(DecPlace + 3) + 'f}',
                    'std(b2)': '{:.' + str(DecPlace) + 'e}',
                    'std(b3)': '{:.' + str(DecPlace) + 'e}'})
            .highlight_min(color='green', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE'])
            .highlight_max(color='red', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE'])
            .highlight_max(color='green', subset='R2')
            .highlight_min(color='red', subset='R2')
            .applymap(lambda x: 'color: orange;' if abs(x) <= 10**(-(DecPlace-1)) else None, subset=['b0', 'b1', 'b2', 'b3', 'std(b0)', 'std(b1)', 'std(b2)', 'std(b3)']))    

print('scipy.optimize.least_squares:'.upper())
display(result_df_least_squares
        .style
            .format(
                precision=DecPlace, na_rep='-',
                formatter={
                    'b1': '{:.' + str(DecPlace + 3) + 'f}',
                    'b2': '{:.' + str(DecPlace) + 'e}',
                    'b3': '{:.' + str(DecPlace) + 'e}',
                    'std(b1)': '{:.' + str(DecPlace + 3) + 'f}',
                    'std(b2)': '{:.' + str(DecPlace) + 'e}',
                    'std(b3)': '{:.' + str(DecPlace) + 'e}'})
            .highlight_min(color='green', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE'])
            .highlight_max(color='red', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE'])
            .highlight_max(color='green', subset='R2')
            .highlight_min(color='red', subset='R2')
            .applymap(lambda x: 'color: orange;' if abs(x) <= 10**(-(DecPlace-1)) else None, subset=['b0', 'b1', 'b2', 'b3', 'std(b0)', 'std(b1)', 'std(b2)', 'std(b3)']))    

print('scipy.optimize.least_squares:'.upper())
display(result_df_leastsq
        .style
            .format(
                precision=DecPlace, na_rep='-',
                formatter={
                    'b1': '{:.' + str(DecPlace + 3) + 'f}',
                    'b2': '{:.' + str(DecPlace) + 'e}',
                    'b3': '{:.' + str(DecPlace) + 'e}',
                    'std(b1)': '{:.' + str(DecPlace + 3) + 'f}',
                    'std(b2)': '{:.' + str(DecPlace) + 'e}',
                    'std(b3)': '{:.' + str(DecPlace) + 'e}'})
            .highlight_min(color='green', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE'])
            .highlight_max(color='red', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE'])
            .highlight_max(color='green', subset='R2')
            .highlight_min(color='red', subset='R2')
            .applymap(lambda x: 'color: orange;' if abs(x) <= 10**(-(DecPlace-1)) else None, subset=['b0', 'b1', 'b2', 'b3', 'std(b0)', 'std(b1)', 'std(b2)', 'std(b3)']))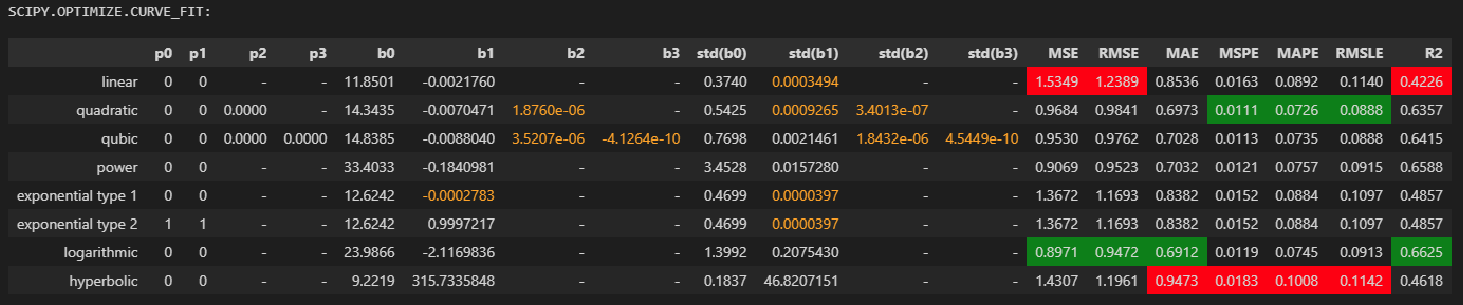

По аналогии с предыдущим примером, сформируем отдельный DataFrame, содержащий ошибки и доверительные интервалы параметров моделей аппроксимации, и сравним с результатами из предыдущих примеров:

result_df_with_perr = pd.DataFrame()

parameter_name_list = ['b0', 'b1', 'b2', 'b3']
result_df_with_perr[parameter_name_list] = result_df[parameter_name_list]

parameter_format_dict = {
    'b0': '{:.' + str(DecPlace) + 'f}',
    'b1': '{:.' + str(DecPlace + 3) + 'f}',
    'b2': '{:.' + str(DecPlace) + 'e}',
    'b3': '{:.' + str(DecPlace) + 'e}',
    'std(b1)': '{:.' + str(DecPlace + 3) + 'f}',
    'std(b2)': '{:.' + str(DecPlace) + 'e}',
    'std(b3)': '{:.' + str(DecPlace) + 'e}'}

for parameter in parameter_name_list:
    for model in result_df.index:
        if not result_df.isna().loc[model, parameter]:
            result_df_with_perr.loc[model, parameter] = \
                str(parameter_format_dict[parameter].format(result_df.loc[model, parameter])) + \
                    ' ' + u"\u00B1" + ' ' + \
                    str(parameter_format_dict[parameter].format(result_df.loc[model, 'std('+parameter+')']))
            relative_errors = abs(result_df.loc[model, 'std('+parameter+')'] / result_df.loc[model, parameter])
            result_df_with_perr.loc[model, 'error('+parameter+')'] = '{:.3%}'.format(relative_errors)

result_df_with_perr_curve_fit = result_df_with_perr.copy()
print('scipy.optimize.curve_fit:'.upper())
display(result_df_with_perr_curve_fit)

print('scipy.optimize.least_squares:'.upper())
display(result_df_with_perr_least_squares)

print('scipy.optimize.leastsq:'.upper())
display(result_df_with_perr_leastsq)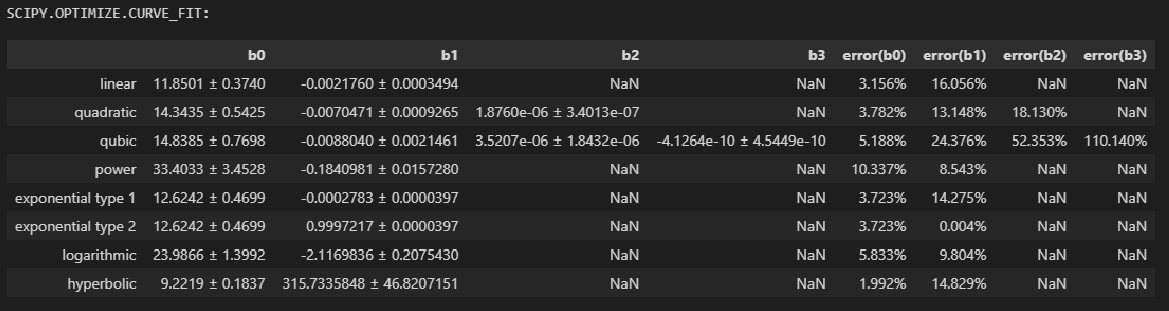

Аппроксимация с использованием scipy.optimize.minimize

Особенности использования функции:

  1. Минимизация значений скалярной функции одной или нескольких переменных; при использовании в качестве функции суммы квадратов получаем реализацию нелинейного метода наименьших квадратов.

  2. Имеется возможность выбора широкого набора алгоритмов оптимизации (Nelder-Mead, Powell, CG, BFGS, Newton-CG, L-BFGS-B, TNC, COBYLA, SLSQP, trust-constr, dogleg, trust-ncg, trust-exact, trust-krylov, custom), получить информацию можно с помощью функции scipy.optimize.show_options (https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.show_options.html#scipy.optimize.show_options), а также есть возможность добавить пользовательский алгоритм оптимизации.

Ссылка на документацию.

Работа с данной функцией принципиально не отличается от разобранных выше, поэтому в целях экономии места в данном обзоре подробности приводить не буду; все рабочие файлы с примерами расчетов доступны в моем репозитории на GitHub (https://github.com/AANazarov/Statistical-methods).

Аппроксимация с использованием библиотеки lmfit

Библиотека lmfit - это универсальный инструмент для решения задач нелинейной оптимизации, в том числе и для аппроксимации зависимостей, представляет собой дальнейшее развитие scipy.optimize.

Особенности использования библиотеки lmfit для аппроксимации:

  1. В качестве переменных вместо обычных чисел типа float используются объекты класса Parameter, которые обладают гораздо более обширным функционалом (https://lmfit.github.io/lmfit-py/parameters.html#lmfit.parameter.Parameter):

    • для них возможно задавать границы допустимых значений и ограничения в виде алгебраических выражений;

    • возможно фиксировать значения в процессе подгонки;

    • после подгонки возможно получить такие атрибуты, как стандартная ошибка и коэффициенты корреляции с другими параметрами модели;

    • возможно указывать размер шага для точек сетки в методе полного перебора и т.д.

  2. Имеется возможность выбора широкого набора алгоритмов оптимизации (leastsq - default, least_squares, differential_evolution, brute, basinhopping, ampgo, nelder, lbfgsb, powell, cg, newton, cobyla, bfgs, tnc, trust-ncg, trust-exact, trust-krylov, trust-constr, dogleg, slsqp, emcee, shgo, dual_annealing) (https://lmfit.github.io/lmfit-py/fitting.html#choosing-different-fitting-methods).

  3. Имеется возможность выбора различных целевых функций минимизации: по умолчанию - сумма квадратов остатков \sum{{r_i}^2}, но в случае, например, наличия выбросов может применяться negentropy - отрицательная энтропия, использующая нормальное распределение \rho \cdot ln(\rho) (где

    \rho = exp(\frac{-\frac{{r_i}^2}{2}}{\sqrt{2\pi}})),

    neglogcauchy - отрицательная логарифмическая вероятность,использующая распределения Коши

    -\sum{ln(\frac{1+{r_i}^2}{\pi})},

    либо callable - функция, определенная пользователем; подробнее см. https://lmfit.github.io/lmfit-py/fitting.html#using-the-minimizer-class.

  4. Улучшена оценка доверительных интервалов. Хотя scipy.optimize.leastsq автоматически вычисляет неопределенности и корреляции из ковариационной матрицы, точность этих оценок иногда вызывает сомнения. Чтобы помочь решить эту проблему, lmfit имеет функции явного исследования пространства параметров и определения уровней доверительной вероятности даже в самых сложных случаях.

  5. Возможность работы с классом Model (https://lmfit.github.io/lmfit-py/model.html#lmfit.model.Model).

  6. Имеется набор встроенных моделей (https://lmfit.github.io/lmfit-py/builtin_models.html#builtin-models-chapter).

  7. Для полного контроля над процессом оптимизации имеется возможность работы с объектом класса Minimizer (https://lmfit.github.io/lmfit-py/fitting.html#using-the-minimizer-class).

  8. Имеются встроенные инструменты вывода отчетов и построения графиков.

Ссылка на документацию к библиотеке: https://lmfit.github.io/lmfit-py/

В документации к библиотеке lmfit приведено большое количество примеров, приведем здесь их описание с целью облегчения поиска полезной информации:

  1. Fit with Data in a pandas DataFrame - аппроксимация по данным содержащимся в pandas DataFrame (https://lmfit.github.io/lmfit-py/examples/example_use_pandas.html#sphx-glr-examples-example-use-pandas-py).

  2. Using an ExpressionModel - использование модуля ExpressionModel для построение моделей с выражениями, определенными пользователем (https://lmfit.github.io/lmfit-py/examples/example_expression_model.html#sphx-glr-examples-example-expression-model-py).

  3. Fit Using Inequality Constraint - использование ограничений типа неравенств (https://lmfit.github.io/lmfit-py/examples/example_fit_with_inequality.html#sphx-glr-examples-example-fit-with-inequality-py).

  4. Fit Using differential_evolution Algorithm - пример использования алгоритма Differential_evolution (https://lmfit.github.io/lmfit-py/examples/example_diffev.html#sphx-glr-examples-example-diffev-py).

  5. Fit Using Bounds - аппроксимация с использованием ограничений параметров (https://lmfit.github.io/lmfit-py/examples/example_fit_with_bounds.html#sphx-glr-examples-example-fit-with-bounds-py).

  6. Fit Specifying Different Reduce Function - использование различных целевых функций минимизации (https://lmfit.github.io/lmfit-py/examples/example_reduce_fcn.html#sphx-glr-examples-example-reduce-fcn-py).

  7. Building a lmfit model with SymPy - построение модели с использованием библиотеки символьных вычислений SymPy (https://lmfit.github.io/lmfit-py/examples/example_sympy.html#sphx-glr-examples-example-sympy-py).

  8. Fit with Algebraic Constraint - аппроксимация с использованием алгебраических ограничений (https://lmfit.github.io/lmfit-py/examples/example_fit_with_algebraic_constraint.html#sphx-glr-examples-example-fit-with-algebraic-constraint-py).

  9. Fit Multiple Data Sets - одновременная подгонка нескольких наборов данных (https://lmfit.github.io/lmfit-py/examples/example_fit_multi_datasets.html#sphx-glr-examples-example-fit-multi-datasets-py).

  10. Fit using the Model interface - использование класса Model (https://lmfit.github.io/lmfit-py/examples/example_Model_interface.html#sphx-glr-examples-example-model-interface-py).

  11. Fit Specifying a Function to Compute the Jacobian - аппроксимация с указанием аналитической функции для вычисления якобиана (для ускорения вычислений) (https://lmfit.github.io/lmfit-py/examples/example_fit_with_derivfunc.html#sphx-glr-examples-example-fit-with-derivfunc-py).

  12. Outlier detection via leave-one-out - обнаружение выбросов методом исключения одного наблюдения (https://lmfit.github.io/lmfit-py/examples/example_detect_outliers.html#sphx-glr-examples-example-detect-outliers-py).

  13. Emcee and the Model Interface - использование алгоритма emcee (https://lmfit.github.io/lmfit-py/examples/example_emcee_Model_interface.html#sphx-glr-examples-example-emcee-model-interface-py). Алгоритм emcee может быть использован для получения апостериорного распределения вероятностей параметров, заданного набором экспериментальных данных, он исследует пространство параметров, чтобы определить распределение вероятностей для параметров, но без явной цели попытаться уточнить решение. Его не следует использовать для аппроксимации, но это полезный метод для более тщательного изучения пространства параметров вокруг решения, он позволяет получить лучшее понимание распределения вероятности для параметров; см. также https://emcee.readthedocs.io/en/stable/.

  14. Complex Resonator Model - в примере показано, как показано, как подобрать параметры сложной модели (резонатора) с помощью lmfit.Model и определения пользовательского класса Model (https://lmfit.github.io/lmfit-py/examples/example_complex_resonator_model.html#sphx-glr-examples-example-complex-resonator-model-py).

  15. Model Selection using lmfit and emcee - в примере показано, как можно использовать алгоритм emcee для выбора байесовской модели (https://lmfit.github.io/lmfit-py/examples/lmfit_emcee_model_selection.html#sphx-glr-examples-lmfit-emcee-model-selection-py).

  16. Calculate Confidence Intervals - расчет доверительных интервалов (https://lmfit.github.io/lmfit-py/examples/example_confidence_interval.html#sphx-glr-examples-example-confidence-interval-py).

  17. Fit Two Dimensional Peaks - в примере показано, как обрабатывать двумерные данные с двухмерными распределениями вероятностей (https://lmfit.github.io/lmfit-py/examples/example_two_dimensional_peak.html#sphx-glr-examples-example-two-dimensional-peak-py).

  18. Global minimization using the brute method (a.k.a. grid search) - глобальная минимизация методом brute (он же поиск по сетке) (https://lmfit.github.io/lmfit-py/examples/example_brute.html#sphx-glr-examples-example-brute-py).

Примеры из документации (Examples from the documentation):

  1. Cоздание и сохранение модели в файл *.sav:

  2. Загрузка модели из файла *.sav:

  3. Создание отчетов:

  4. Работа с доверительными интервалами:

  5. Аппроксимация вероятностных распределений:

  6. Различные опции lmfit:

  7. Использование различных встроенных моделей:

Вначале рассмотрим различные приемы аппроксимации в lmfit:

  • пример 1 - аппроксимация с использованием интерфейса Model (самый простой случай);

  • пример 2 - аппроксимация с использованием интерфейса Model и объекта класса Parameter, расчетом доверительных интервалов;

  • пример 3 - аппроксимация с использованием функции minimize;

  • пример 4 - аппроксимация c использованием объекта класса Minimazer.

Затем рассмотрим различные частные случаи аппроксимации в lmfit:

  • пример 5 - аппроксимация с заданием начальных значений (initial values) (на примере экспоненциальной зависимости I типа);

  • пример 6 - аппроксимация c использованием встроенных моделей библиотеки lmfit;

  • пример 7 - аппроксимация c использованием методов глобального поиска;

  • пример 8 - обнаружение выбросов (outlier detection) при аппроксимации

Пример 1 - аппроксимация с использованием интерфейса Model (самый простой случай)

Для начала рассмотрим самую обычную аппроксимацию на примере линейной зависимости, для подгонки параметров модели используем метод fit класса Model.

Пояснения к расчету:

  1. Вначале исходные данные - двумерную таблицу (X1, Y) - приводим к виду, отсортированному по возрастанию переменной X1, для того, чтобы встроенные графические возможности библиотеки lmfit корректно отображали информацию.

  2. С помощью lmfit.Model создаем модель.

  3. С помощью model.fit выполняем аппроксимацию (нахождение параметров). По умолчанию используется алгоритм Левенберга-Марквардта (Levenberg–Marquardt algorithm) (leastsq, least_squares).

  4. С помощью result.fit_report выводим отчет с результатами, который содержит:

    • метрики качества аппроксимации: chi-square - в данном случае сумма квадратов остатков \chi^2 = \sum{{e_i}^2} (т.е. по сути SSE), reduced chi-square

      {\chi}_y^2 = \frac{\chi^2}{N-N_{varys}} и R^2;

    • информационные критерии Акаике и Байеса;

    • параметры модели b_0 и b_1 с их стандратными ошибками, относительными ошибками в % и начальными условиями (init);

    • коэффициенты корреляции между параметрами C(b0, b1).

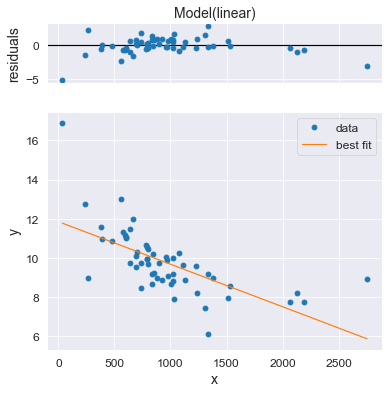
  5. Выводим различные виды графиков:

    • result.plot_fit() - обычный точечный график;

    • result.plot_residuals() - график остатков;

    • result.plot() - точечный график, совмещенный с графиком остатков.

import lmfit
print('{:<35}{:^0}'.format("Текущая версия модуля lmfit: ", lmfit.__version__), '\n')

# Preparation of input data
dataset_sort_df = dataset_df.loc[:, ['X1', 'Y']].sort_values(by=['X1'])
#display(dataset_sort_df)
Y_sort = np.array(dataset_sort_df['Y'])
#print(Y_sort, type(Y_sort), len(Y_sort))
X_sort = np.array(dataset_sort_df['X1'])
#print(X_sort, type(X_sort), len(X_sort))

# LINEAR MODEL
func_name = 'linear'
print(f'{func_name.upper()} MODEL: {formulas_dict[func_name]}')
func = models_dict[func_name]
p0 = p0_dict[func_name]
model = lmfit.Model(func, independent_vars=['x'], name=func_name)
result = model.fit(Y_sort, x=X_sort, b0=p0[0], b1=p0[1])
print(result.fit_report())
result.plot_fit()
plt.show()
result.plot_residuals()
plt.show()
result.plot()
plt.show()

Текущая версия модуля lmfit:       1.1.0 

LINEAR MODEL: y = b0 + b1*x
[[Model]]
    Model(linear)
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 7
    # data points      = 55
    # variables        = 2
    chi-square         = 84.4203915
    reduced chi-square = 1.59283758
    Akaike info crit   = 27.5661686
    Bayesian info crit = 31.5808350
    R-squared          = 0.42259718
[[Variables]]
    b0:  11.8501350 +/- 0.37396000 (3.16%) (init = 0)
    b1: -0.00217603 +/- 3.4938e-04 (16.06%) (init = 0)
[[Correlations]] (unreported correlations are < 0.100)
    C(b0, b1) = -0.890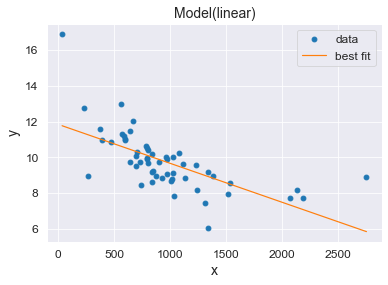

Пример 2 - аппроксимация с использованием интерфейса Model и объекта класса Parameter, расчетом доверительных интервалов

Рассмотрим аппроксимацию с более широким использованием возможностей библиотеки lmfit на примере степенной зависимости:

Пояснения к расчету:

  1. Исходные данные также должны быть отсортированы по возрастанию переменной X1.

  2. Также с помощью lmfit.Model создаем модель.

  3. С помощью model.make_params задаем свойства параметров модели (в этом примере мы просто задаем начальные значения параметров, не затрагивая прочие атрибуты - минимальные и максимальные значения, алгебраические ограничения и т.д.).

  4. Также с помощью model.fit выполняем аппроксимацию (нахождение параметров), при этом расширим набор используемых настроек - добавим method и nan_policy (правда, значения установим по умолчанию leastsq и raise).

  5. Также с помощью result.fit_report выводим отчет с результатами, при этом установим ограничение на коэффициент корреляции между параметрами (min_correl=0.2).

  6. С помощью result.params.pretty_print() выведем отчет о параметрах модели.

  7. С помощью result.ci_report() выведем отчет о границах доверительных интервалов для параметров модели.

  8. С помощью result.eval_components и result.eval выведем расчетные значения модели: в первом случае - в виде словаря (dict), во-втором случае - в виде массива (numpy.ndarray).

  9. С помощью result.eval_uncertainty выведем ширину доверительного интервала для расчетных значений.

  10. По аналогии с предыдущим примером выведем графики result.plot_fit() и result.plot_residuals() с настройкой их атрибутов (размер окна, подписи осей и пр.).

  11. Дополнительно выведем графики двух видов:

    • на первом графике будут отображаться фактические данные (data), расчетные данные по модели аппроксимации (best fit) и также доверительный интервал шириной 3\sigma;

    • на втором графике будет отображаться остатки (residuals).

Замечание касательно расчета доверительных интервалов: для отдельных моделей lmfit может выдавать ошибку Cannot determine Confidence Intervals without sensible uncertainty estimates, в этом случае необходимо установить пакет numdifftools (https://pypi.org/project/numdifftools/).

# POWER MODEL
func_name = 'power'
print(f'{func_name.upper()} MODEL: {formulas_dict[func_name]}')

# define objective function
func = models_dict[func_name]

# initial values
p0 = p0_dict[func_name]

# create a Model
model = lmfit.Model(func,   
                    independent_vars=['x'],
                    name=func_name)

# create a set of Parameters
params = model.make_params(b0=p0[0],
                           b1=p0[1])

# calculations
result = model.fit(Y_sort, params, x=X_sort,
                   method='leastsq',
                   nan_policy='raise')

# report of the fitting results (https://lmfit.github.io/lmfit-py/model.html#lmfit.model.ModelResult.fit_report)
print(f'result.fit_report:\n{result.fit_report(min_correl=0.2)}\n')

# report of parameters data (https://lmfit.github.io/lmfit-py/parameters.html#lmfit.parameter.Parameters.pretty_print)
print('result.params.pretty_print():')
result.params.pretty_print()
print('\n')

# report of the confidence intervals (https://lmfit.github.io/lmfit-py/confidence.html#lmfit.ci_report)
print(f'result.ci_report:\n{result.ci_report()}\n')

# evaluate each component of a composite model function (https://lmfit.github.io/lmfit-py/model.html#lmfit.model.ModelResult.eval_components)
comps = result.eval_components(x=X_sort)
print(f'result.eval_components = \n{comps}\n')

# evaluate the uncertainty of the model function (https://lmfit.github.io/lmfit-py/model.html#lmfit.model.ModelResult.eval_uncertainty)
dely = result.eval_uncertainty(sigma=3)
print(f'result.eval_uncertainty(sigma=3) = \n{dely}\n')

# graphic (data, best-fit, uncertainty band and residuals)
fig, axes = plt.subplots(2, 1, figsize=(297/INCH, 210/INCH))
fig.suptitle(f'Model({func_name})', fontsize=16)

#label = func_name + ' '+ r'$(R^2 = $' + f'{R2}' + ', ' + f'RMSE = {RMSE}' + ', ' + f'MAE = {MAE}' + ', ' + f'MSPE = {MSPE}' + ', ' + f'MAPE = {MAPE})'
axes[0].set_title('data, best-fit, and uncertainty band')
sns.scatterplot(x=X_sort, y=Y_sort, label='data', s=50, color='red', ax=axes[0])
R2 = round(result.rsquared, DecPlace)
sns.lineplot(x=X_sort, y=result.best_fit, color='blue', linewidth=2, legend=True, label='best fit (' + r'$R^2 = $' + f'{R2})', ax=axes[0])
axes[0].fill_between(X_sort, result.best_fit-dely, result.best_fit+dely, color="grey", alpha=0.3, label=r'3-$\sigma$ band')
axes[0].legend()
axes[0].set_ylabel('Y')
#axes[0].set_xlim(X1_min_graph, X1_max_graph)
#axes[0].set_ylim(Y_min_graph, Y_max_graph)

sns.scatterplot(x=X_sort, y=-result.residual, ax=axes[1], s=50)
axes[1].axhline(y = 0, color = 'k', linewidth = 1)
axes[1].set_xlabel('X')
axes[1].set_ylabel('residuals')
#axes[1].set_xlim(X1_min_graph, X1_max_graph)
#axes[1].set_ylim(Y_min_graph, Y_max_graph)

plt.show()
POWER MODEL: y = b0*x^b1
result.fit_report:
[[Model]]
    Model(power)
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 29
    # data points      = 55
    # variables        = 2
    chi-square         = 49.8796865
    reduced chi-square = 0.94112616
    Akaike info crit   = -1.37456420
    Bayesian info crit = 2.64010217
    R-squared          = 0.65884224
[[Variables]]
    b0:  33.4032965 +/- 3.45275807 (10.34%) (init = 0)
    b1: -0.18409814 +/- 0.01572801 (8.54%) (init = 0)
[[Correlations]] (unreported correlations are < 0.200)
    C(b0, b1) = -0.992

result.params.pretty_print():
Name     Value      Min      Max   Stderr     Vary     Expr Brute_Step
b0      33.4     -inf      inf    3.453     True     None     None
b1   -0.1841     -inf      inf  0.01573     True     None     None


result.ci_report:
       99.73%    95.45%    68.27%    _BEST_    68.27%    95.45%    99.73%
 b0:  -9.61176  -6.50967  -3.33032  33.40330  +3.57568  +7.51972 +11.99711
 b1:  -0.04701  -0.03103  -0.01551  -0.18410  +0.01594  +0.03283  +0.05128

result.eval_components = 
{'power': array([17.1825, 12.2259, 11.9584, 11.2070, 11.1216, 10.7403, 10.4265,
       10.3691, 10.3104, 10.2881, 10.2818, 10.1608, 10.1608, 10.0915,
       10.0161, 10.0087,  9.9898,  9.9158,  9.8985,  9.7892,  9.7778,
        9.7755,  9.7687,  9.7574,  9.7507,  9.6757,  9.6744,  9.6691,
        9.6450,  9.5917,  9.5481,  9.4926,  9.4354,  9.4156,  9.4067,
        9.3493,  9.3306,  9.3222,  9.3222,  9.3106,  9.2345,  9.1804,
        9.1564,  9.0159,  9.0065,  8.9122,  8.8808,  8.8796,  8.8268,
        8.6752,  8.6554,  8.1915,  8.1472,  8.1083,  7.7727])}

result.eval_uncertainty(sigma=3) = 
[2.5746 0.8186 0.7464 0.5692 0.5522 0.4861 0.4464 0.4407 0.4355 0.4337
 0.4332 0.4249 0.4249 0.4213 0.4183 0.4180 0.4174 0.4158 0.4155 0.4151
 0.4151 0.4151 0.4152 0.4153 0.4154 0.4167 0.4167 0.4168 0.4174 0.4191
 0.4208 0.4234 0.4265 0.4277 0.4282 0.4320 0.4333 0.4339 0.4339 0.4348
 0.4408 0.4454 0.4476 0.4613 0.4623 0.4726 0.4762 0.4763 0.4825 0.5013
 0.5039 0.5682 0.5747 0.5804 0.6303]

Пример 3 - аппроксимация c использованием функции minimize

Про функцию minimize подробнее см. https://lmfit.github.io/lmfit-py/fitting.html#the-minimize-function.

# POWER MODEL
func_name = 'power'
print(f'{func_name.upper()} MODEL: {formulas_dict[func_name]}')

# define objective function
func = models_dict[func_name]

# initial values
p0 = p0_dict[func_name]

# create a set of Parameters
params = lmfit.Parameters()
params.add('b0', value=p0[0], min=-inf, max=inf)
params.add('b1', value=p0[1], min=-inf, max=inf)

# function for calculating residuals
residual_func = lambda params, x, ydata: func(x, params['b0'].value, params['b1'].value) - ydata

# calculations
result = lmfit.minimize(residual_func, params, args=(X_sort, Y_sort))
lmfit.report_fit(result)
#print(lmfit.fit_report(result))    # other type of output
best_fit = Y_sort + result.residual
POWER MODEL: y = b0*x^b1
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 29
    # data points      = 55
    # variables        = 2
    chi-square         = 49.8796865
    reduced chi-square = 0.94112616
    Akaike info crit   = -1.37456420
    Bayesian info crit = 2.64010217
[[Variables]]
    b0:  33.4032965 +/- 3.45275807 (10.34%) (init = 0)
    b1: -0.18409814 +/- 0.01572801 (8.54%) (init = 0)
[[Correlations]] (unreported correlations are < 0.100)
    C(b0, b1) = -0.992

Пример 4 - аппроксимация c использованием объекта класса Minimazer

Про класс Minimazer подробнее см. https://lmfit.github.io/lmfit-py/fitting.html#using-the-minimizer-class.

# POWER MODEL
func_name = 'power'
print(f'{func_name.upper()} MODEL: {formulas_dict[func_name]}')

# define objective function
func = models_dict[func_name]

# initial values
p0 = p0_dict[func_name]

# create a set of Parameters
params = lmfit.Parameters()
params.add('b0', value=p0[0], min=-inf, max=inf)
params.add('b1', value=p0[1], min=-inf, max=inf)

# function for calculating residuals
residual_func = lambda params, x, ydata: func(x, params['b0'].value, params['b1'].value) - ydata

# create Minimizer
minner = lmfit.Minimizer(residual_func, params, fcn_args=(X_sort, Y_sort), nan_policy='omit')

# calculations
result = minner.minimize()
#print(f'\nfirst solve with {method_1.upper()} algorithm:')
lmfit.report_fit(result)
#print(lmfit.fit_report(result))    # other type of output
best_fit = Y_sort + result.residual
#print(best_fit)

# calculate the confidence intervals for parameters
ci, tr = lmfit.conf_interval(minner, result, sigmas=[3], trace=True)
print('\nreport_ci(ci):')
lmfit.report_ci(ci)

# graphic (data, best-fit, and residuals)
fig, axes = plt.subplots(2, 1, figsize=(297/INCH, 210/INCH))
fig.suptitle(f'Model({func_name})', fontsize=16)

sns.scatterplot(x=X_sort, y=Y_sort, label='data', s=50, color='red', ax=axes[0])
sns.lineplot(x=X_sort, y=best_fit, color='blue', linewidth=2, legend=True, label='best fit', ax=axes[0])
axes[0].set_ylabel('Y')
#axes[0].set_xlim(X1_min_graph, X1_max_graph)
#axes[0].set_ylim(Y_min_graph, Y_max_graph)

sns.scatterplot(x=X_sort, y=-result.residual, ax=axes[1], s=50)
axes[1].axhline(y = 0, color = 'k', linewidth = 1)
axes[1].set_xlabel('X')
axes[1].set_ylabel('residuals')
#axes[1].set_xlim(X1_min_graph, X1_max_graph)
#axes[1].set_ylim(Y_min_graph, Y_max_graph)

plt.show()
POWER MODEL: y = b0*x^b1
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 29
    # data points      = 55
    # variables        = 2
    chi-square         = 49.8796865
    reduced chi-square = 0.94112616
    Akaike info crit   = -1.37456420
    Bayesian info crit = 2.64010217
[[Variables]]
    b0:  33.4032965 +/- 3.45275807 (10.34%) (init = 0)
    b1: -0.18409814 +/- 0.01572801 (8.54%) (init = 0)
[[Correlations]] (unreported correlations are < 0.100)
    C(b0, b1) = -0.992

report_ci(ci):
       99.73%    _BEST_    99.73%
 b0:  -9.61177  33.40330 +11.99711
 b1:  -0.04701  -0.18410  +0.05128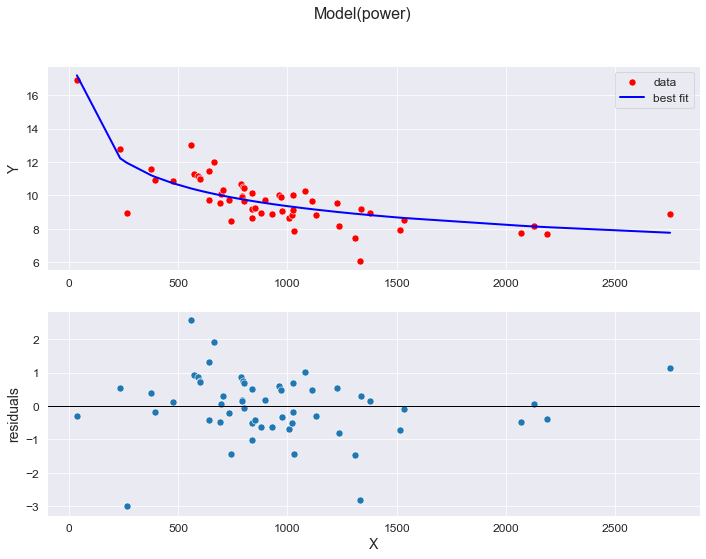

Пример 5 - аппроксимация с заданием начальных значений (initial values)

Некоторые модели при аппроксимации требуют задания начальных значений - для успешной реализации алгоритма заданием нулей или единиц в качестве p0 не обойтись. Рассмотрим аппроксимацию экспоненциальной модели I типа с заданием начальных условий, при этом воспользуемся возможностью библиотеки lmfit вывести на график зависимость с оптимальными параметрами (best fit) и зависимость с начальными параметрами (init fit) это наглядно демонстрирует, как улучшается модель в процессе поиска оптимальных параметров.

# EXPONENTIAL MODEL TYPE I: y = b0*exp(b1^x)
func_name = 'exponential type 1'
print(f'{func_name.upper()} MODEL: {formulas_dict[func_name]}')

# define objective function
func = models_dict[func_name]

# initial values
n = len(Y_sort)
(x1, x2, y1, y2) = (X_sort[0], X_sort[n-1], Y_sort[0], Y_sort[n-1])
p0_b0 = y2 * np.exp(np.log(y2/y1) * x2/(x1-x2))
p0_b1 = -np.log(y2/y1) / (x1-x2)
p0 = [p0_b0, p0_b1]
print(f'p0 = {p0}')

# create a Model
model = lmfit.Model(func,   
                    independent_vars=['x'],
                    name=func_name)

# create a set of Parameters
params = lmfit.Parameters()
params.add('b0', value=p0[0], min=-inf, max=inf)
params.add('b1', value=p0[1], min=-inf, max=inf)

# calculations
result = model.fit(Y_sort, params, x=X_sort,
                   method='leastsq',
                   nan_policy='raise')

# report of the fitting results (https://lmfit.github.io/lmfit-py/model.html#lmfit.model.ModelResult.fit_report)
print(f'result.fit_report:\n{result.fit_report(min_correl=0.2)}\n')

# report of the confidence intervals (https://lmfit.github.io/lmfit-py/confidence.html#lmfit.ci_report)
print(f'result.ci_report:\n{result.ci_report()}\n')

# evaluate the uncertainty of the model function (https://lmfit.github.io/lmfit-py/model.html#lmfit.model.ModelResult.eval_uncertainty)
dely = result.eval_uncertainty(sigma=3)

# graphic (data, best-fit, uncertainty band and residuals)
fig, axes = plt.subplots(2, 1, figsize=(297/INCH, 210/INCH))
fig.suptitle(f'Model({func_name})', fontsize=16)

axes[0].set_title('data, init-fit, best-fit, and uncertainty band')
sns.scatterplot(x=X_sort, y=Y_sort, label='data', s=50, color='red', ax=axes[0])
sns.lineplot(x=X_sort, y=result.init_fit, color='cyan', linewidth=2, linestyle='dotted', legend=True, label='init fit', ax=axes[0])
R2 = round(result.rsquared, DecPlace)
sns.lineplot(x=X_sort, y=result.best_fit, color='blue', linewidth=2, legend=True, label='best fit (' + r'$R^2 = $' + f'{R2})', ax=axes[0])
axes[0].fill_between(X_sort, result.best_fit-dely, result.best_fit+dely, color="grey", alpha=0.3, label=r'3-$\sigma$ band')
axes[0].legend()
axes[0].set_ylabel('Y')
#axes[0].set_xlim(X1_min_graph, X1_max_graph)
#axes[0].set_ylim(Y_min_graph, Y_max_graph)

sns.scatterplot(x=X_sort, y=-result.residual, ax=axes[1], s=50)
axes[1].axhline(y = 0, color = 'k', linewidth = 1)
axes[1].set_xlabel('X')
axes[1].set_ylabel('residuals')
#axes[1].set_xlim(X1_min_graph, X1_max_graph)
#axes[1].set_ylim(Y_min_graph, Y_max_graph)

plt.show()
EXPONENTIAL TYPE 1 MODEL: y = b0*exp(b1^x)
p0 = [17.037879730518267, -0.00023560415890108336]
result.fit_report:
[[Model]]
    Model(exponential type 1)
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 19
    # data points      = 55
    # variables        = 2
    chi-square         = 75.1949111
    reduced chi-square = 1.41877191
    Akaike info crit   = 21.2012704
    Bayesian info crit = 25.2159368
    R-squared          = 0.48569589
[[Variables]]
    b0:  12.6241795 +/- 0.46994783 (3.72%) (init = 17.03788)
    b1: -2.7834e-04 +/- 3.9734e-05 (14.27%) (init = -0.0002356042)
[[Correlations]] (unreported correlations are < 0.200)
    C(b0, b1) = -0.899

result.ci_report:
       99.73%    95.45%    68.27%    _BEST_    68.27%    95.45%    99.73%
 b0:  -1.48083  -0.98324  -0.49401  12.62418  +0.51299  +1.06128  +1.66495
 b1:  -0.00014  -0.00009  -0.00004  -0.00028  +0.00004  +0.00009  +0.00013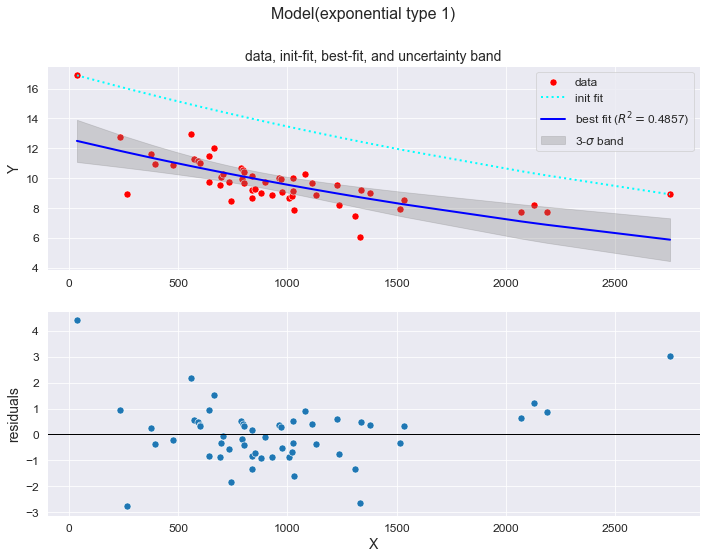

Пример 6 - аппроксимация с использованием встроенных моделей библиотеки lmfit

Рассмотрим аппроксимацию с использованием встроенных моделей библиотеки lmfit. Набор этих моделей достаточно обширен (подробнее см. https://lmfit.github.io/lmfit-py/builtin_models.html,
https://lmfit.github.io/lmfit-py/examples/documentation/model_uncertainty2.html#sphx-glr-examples-documentation-model-uncertainty2-py), при этом для представляют интерес следующие модели:

  • линейная LinearModel;

  • квадратическая QuadraticModel;

  • полиномиальная PolynomialModel (мы рассмотрим случай m=3 - кубическую модель);

  • экспоненциальная ExponentialModel;

  • степенная PowerLawModel.

При этом необходимо учитывать, что встроенные модели в библиотеке lmfit имеют свой формализованный вид и параметры, заданные в виде служебных слов, которые нужно учитывать в программном коде (так, например, параметры линейной модели имеют названия slope и intercept):

Наименование

Уравнение

Параметры и их названия в программном коде

Ссылка

LinearModel

f(x;m,b)=mx+b

slope (m), intercept (b)

https://lmfit.github.io/lmfit-py/builtin_models.html#lmfit.models.LinearModel

QuadraticModel

f(x;a,b,c)=ax^2+bx+c

a, b, c

https://lmfit.github.io/lmfit-py/builtin_models.html#lmfit.models.QuadraticModel

PolynomialModel

f(x;c_0,c_1...c_7)=\sum{c_ix^i}

c0...c1

https://lmfit.github.io/lmfit-py/builtin_models.html#lmfit.models.PolynomialModel

ExponentialModel

f(x;A,\tau)=Ae^{-x/\tau}

amplitude (A), decay (\tau)

https://lmfit.github.io/lmfit-py/builtin_models.html#lmfit.models.ExponentialModel

PowerLawModel

f(x;A,k)=Ax^k

amplitude (A), exponent (k)

https://lmfit.github.io/lmfit-py/builtin_models.html#lmfit.models.PowerLawModel

Для экспоненциальной модели ExponentialModel мы оценим начальные значения параметров с помощью метода Model.guess (https://lmfit.github.io/lmfit-py/model.html#model-class-methods).

# list of model
model_list = ['linear', 'quadratic', 'qubic', 'power', 'exponential type 1']

# model reference
model_exponential_type_1 = lmfit.models.ExponentialModel(prefix='exponential_type_1_')
model_dict = {
        'linear':             lmfit.models.LinearModel(prefix='linear_'),
        'quadratic':          lmfit.models.QuadraticModel(prefix='quadratic_'),
        'qubic':              lmfit.models.PolynomialModel(degree=3, prefix='qubic_'),
        'power':              lmfit.models.PowerLawModel(prefix='power_'),
        'exponential type 1': model_exponential_type_1}

# create a set of Parameters
params_dict = dict()

params_linear = lmfit.Parameters()
params_linear.add('linear_intercept',    value = 0, min = -inf, max = inf)
params_linear.add('linear_slope',        value = 0, min = -inf, max = inf)
params_dict['linear'] = params_linear

params_quadratic = lmfit.Parameters()
params_quadratic.add('quadratic_a',    value = 0, min = -inf, max = inf)
params_quadratic.add('quadratic_b',    value = 0, min = -inf, max = inf)
params_quadratic.add('quadratic_c',    value = 0, min = -inf, max = inf)
params_dict['quadratic'] = params_quadratic

params_qubic = lmfit.Parameters()
params_qubic.add('qubic_c0',    value = 0, min = -inf, max = inf)
params_qubic.add('qubic_c1',    value = 0, min = -inf, max = inf)
params_qubic.add('qubic_c2',    value = 0, min = -inf, max = inf)
params_qubic.add('qubic_c3',    value = 0, min = -inf, max = inf)
params_dict['qubic'] = params_qubic

params_power = lmfit.Parameters()
params_power.add('power_amplitude',    value = 0, min = -inf, max = inf)
params_power.add('power_exponent',     value = 0, min = -inf, max = inf)
params_dict['power'] = params_power

params_exponential_type_1 = lmfit.Parameters()
#params_exponential_type_1.add('exponential_type_1_amplitude',    value = 0, min = -inf, max = inf)
#params_exponential_type_1.add('exponential_type_1_decay',        value = 0, min = -inf, max = inf)
pars_exponential_type_1 = model_exponential_type_1.guess(Y_sort, x=X_sort)
params_dict['exponential type 1'] = pars_exponential_type_1

# calculations
result_dict = dict()
for func_name in model_list:
    model = model_dict[func_name]
    result = model.fit(Y_sort, params_dict[func_name], x=X_sort)
    print(f'{func_name.upper()} MODEL:\n{result.fit_report(min_correl=0.2)}\n')
    result_dict[func_name] = result

# graphic 1 (various models)
fig, axes = plt.subplots(figsize=(420/INCH, 297/INCH))
#fig.suptitle(f'Model(various models)', fontsize=16)
axes.set_title('Model(various models)', fontsize=16)
sns.scatterplot(x=X_sort, y=Y_sort, label='data', s=50, color='red', ax=axes)
for func_name in model_list:
        result = result_dict[func_name]
        R2 = round(result.rsquared, DecPlace)
        label = func_name + ' (' + r'$R^2 = $' + f'{R2})'
        sns.lineplot(x=X_sort, y=result.best_fit, linewidth=2, color=color_dict[func_name], legend=True, label=label, ax=axes)    # the color_dict was defined earlier
plt.show()

# graphic 2 (various models)
number_models = len(model_list)
fig, axes = plt.subplots(2, number_models, figsize=(210/INCH*number_models, 297/INCH))
fig.suptitle('Model(various models)', fontsize=20)
for i, func_name in enumerate(model_list):
        ax1 = plt.subplot(2, number_models, i+1)
        ax2 = plt.subplot(2, number_models, i+1+number_models)
        ax1.set_title(f'Model({func_name})', fontsize=16)
        result = result_dict[func_name]
        dely = result.eval_uncertainty(sigma=3)
        sns.scatterplot(x=X_sort, y=Y_sort, label='data', s=50, color='red', ax=ax1)
        R2 = round(result.rsquared, DecPlace)
        label = func_name + ' (' + r'$R^2 = $' + f'{R2})'
        sns.lineplot(x=X_sort, y=result.best_fit, linewidth=2, color=color_dict[func_name], legend=True, label=label, ax=ax1)    # the color_dict was defined earlier
        ax1.fill_between(X_sort, result.best_fit-dely, result.best_fit+dely, color="grey", alpha=0.3, label=r'3-$\sigma$ band')
        ax1.legend()
        ax1.set_ylabel('Y')
        sns.scatterplot(x=X_sort, y=-result.residual, ax=ax2, s=50)
        ax2.axhline(y = 0, color = 'k', linewidth = 1)
        ax2.set_xlabel('X')
        ax2.set_ylabel('residuals')
plt.show()
LINEAR MODEL:
[[Model]]
    Model(linear, prefix='linear_')
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 7
    # data points      = 55
    # variables        = 2
    chi-square         = 84.4203915
    reduced chi-square = 1.59283758
    Akaike info crit   = 27.5661686
    Bayesian info crit = 31.5808350
    R-squared          = 0.42259718
[[Variables]]
    linear_intercept:  11.8501350 +/- 0.37396000 (3.16%) (init = 0)
    linear_slope:     -0.00217603 +/- 3.4938e-04 (16.06%) (init = 0)
[[Correlations]] (unreported correlations are < 0.200)
    C(linear_intercept, linear_slope) = -0.890

QUADRATIC MODEL:
[[Model]]
    Model(parabolic, prefix='quadratic_')
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 13
    # data points      = 55
    # variables        = 3
    chi-square         = 53.2610253
    reduced chi-square = 1.02425049
    Akaike info crit   = 4.23294056
    Bayesian info crit = 10.2549401
    R-squared          = 0.63571519
[[Variables]]
    quadratic_a:  1.8760e-06 +/- 3.4013e-07 (18.13%) (init = 0)
    quadratic_b: -0.00704710 +/- 9.2652e-04 (13.15%) (init = 0)
    quadratic_c:  14.3434596 +/- 0.54247230 (3.78%) (init = 0)
[[Correlations]] (unreported correlations are < 0.200)
    C(quadratic_a, quadratic_b) = -0.953
    C(quadratic_b, quadratic_c) = -0.943
    C(quadratic_a, quadratic_c) = 0.833

QUBIC MODEL:
[[Model]]
    Model(polynomial, prefix='qubic_')
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 16
    # data points      = 55
    # variables        = 4
    chi-square         = 52.4138335
    reduced chi-square = 1.02772223
    Akaike info crit   = 5.35105531
    Bayesian info crit = 13.3803880
    R-squared          = 0.64150965
[[Variables]]
    qubic_c0:  14.8384962 +/- 0.76977661 (5.19%) (init = 0)
    qubic_c1: -0.00880398 +/- 0.00214609 (24.38%) (init = 0)
    qubic_c2:  3.5207e-06 +/- 1.8432e-06 (52.35%) (init = 0)
    qubic_c3: -4.1264e-10 +/- 4.5449e-10 (110.14%) (init = 0)
[[Correlations]] (unreported correlations are < 0.200)
    C(qubic_c2, qubic_c3) = -0.983
    C(qubic_c1, qubic_c2) = -0.962
    C(qubic_c0, qubic_c1) = -0.927
    C(qubic_c1, qubic_c3) = 0.902
    C(qubic_c0, qubic_c2) = 0.805
    C(qubic_c0, qubic_c3) = -0.708

POWER MODEL:
[[Model]]
    Model(powerlaw, prefix='power_')
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 29
    # data points      = 55
    # variables        = 2
    chi-square         = 49.8796865
    reduced chi-square = 0.94112616
    Akaike info crit   = -1.37456420
    Bayesian info crit = 2.64010217
    R-squared          = 0.65884224
[[Variables]]
    power_amplitude:  33.4032965 +/- 3.45275807 (10.34%) (init = 0)
    power_exponent:  -0.18409814 +/- 0.01572801 (8.54%) (init = 0)
[[Correlations]] (unreported correlations are < 0.200)
    C(power_amplitude, power_exponent) = -0.992

EXPONENTIAL TYPE 1 MODEL:
[[Model]]
    Model(exponential, prefix='exponential_type_1_')
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 16
    # data points      = 55
    # variables        = 2
    chi-square         = 75.1949111
    reduced chi-square = 1.41877191
    Akaike info crit   = 21.2012705
    Bayesian info crit = 25.2159368
    R-squared          = 0.48569589
[[Variables]]
    exponential_type_1_amplitude:  12.6242247 +/- 0.46996177 (3.72%) (init = 11.84731)
    exponential_type_1_decay:      3592.61300 +/- 512.762035 (14.27%) (init = 4650.427)
[[Correlations]] (unreported correlations are < 0.200)
    C(exponential_type_1_amplitude, exponential_type_1_decay) = -0.899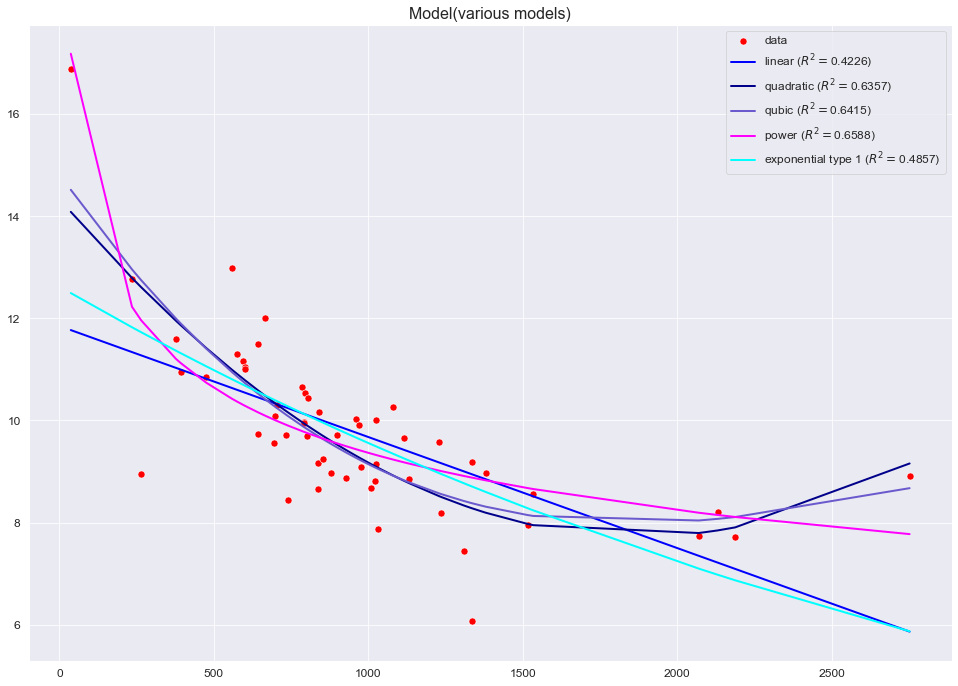

Пример 7 - аппроксимация с использованием методов глобального поиска

Рассмотрим более сложный случай на примере логистической зависимости I типа

Y=\frac{b_0}{1+b_1\cdot e^{-b_2\cdot X}}.

Обычно аппроксимация подобных зависимостей требует более тщательного подхода по сравнению с разобранными ранее примерами - необходимо варьировать алгоритмы, предварительно оценивать начальные точки для приближения (методом трех точек и т.д.). В этом случае эффективными могут оказаться методы глобального поиска.

В рамках данного обзора у нас нет возможности сильно углубляться в данную тему, поэтому просто проиллюстрируем возможности lmfit - проведем аппроксимацию в два этапа:

  1. Вначале оценим параметры зависимости алгоритмом basinhopping (см. https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.basinhopping.html, https://machinelearningmastery.com/basin-hopping-optimization-in-python/).

  2. Проверим оценку параметров алгоритмом глобальной оптимизации по сетке brute (см. https://lmfit.github.io/lmfit-py/examples/example_brute.html).

logistic_type_1_func = lambda x, b0, b1, b2: b0 / (1 + b1*np.exp(-b2*x))

# LOGISTIC MODEL TYPE I: y = b0 / (1 + b1*np.exp(-b2*x))
print('LOGISTIC MODEL TYPE I: y = b0 / (1 + b1*np.exp(-b2*x))')

# define objective function
func = logistic_type_1_func
func_name = 'logistic type 1'

# initial values
p0 = [0, 0, 0]

# create a set of Parameters
params = lmfit.Parameters()
params.add('b0', value=p0[0], min=-inf, max=inf, brute_step=0.01)
params.add('b1', value=p0[1], min=-inf, max=inf, brute_step=0.01)
params.add('b2', value=p0[2], min=-inf, max=inf, brute_step=0.001)

# function for calculating residuals
residual_func = lambda params, x, ydata: func(x, params['b0'].value,
                                                 params['b1'].value,
                                                 params['b2'].value
                                                 ) - ydata

# create Minimizer
minner = lmfit.Minimizer(residual_func, params, fcn_args=(X_sort, Y_sort), nan_policy='omit')

# first solve with basinhopping algorithm
method_1 = 'basinhopping'
result_1 = minner.minimize(method=method_1)
print(f'\nfirst solve with {method_1.upper()} algorithm:')
lmfit.report_fit(result_1)
#print(lmfit.fit_report(result_1))
best_fit_1 = Y_sort + result_1.residual
#print(best_fit_1)

# then solve with brute algorithm using the basinhopping solution as a starting point
method_2 = 'brute'
result_2 = minner.minimize(method=method_2,
                           params=result_1.params,
                           Ns=30,
                           keep=30)
print(f'\nsecond solve with {method_2.upper()} algorithm using the {method_1.upper()} solution as a starting point:')
#lmfit.report_fit(result_2)
print(lmfit.fit_report(result_2))
best_fit_2 = Y_sort + result_2.residual
#print(best_fit_2)

# calculate the confidence intervals for parameters
ci, tr = lmfit.conf_interval(minner, result_2, sigmas=[3], trace=True)
lmfit.report_ci(ci)
#print(tr)

# graphics
fig, axes = plt.subplots(2, 1, figsize=(297/INCH, 210/INCH))
fig.suptitle(f'Model({func_name})', fontsize=14)

axes[0].set_title('data, first fit and second fit')
sns.scatterplot(x=X_sort, y=Y_sort, label='data', s=50, color='red', ax=axes[0])
sns.lineplot(x=X_sort, y=best_fit_1, color='cyan', linewidth=6, legend=True, label=f'first fit ({method_1})', ax=axes[0])
sns.lineplot(x=X_sort, y=best_fit_2, color='blue', linewidth=2, legend=True, label=f'second fit ({method_2})', ax=axes[0])
axes[0].set_ylabel('Y')

sns.scatterplot(x=X_sort, y=-result_2.residual, ax=axes[1], s=50)
axes[1].axhline(y = 0, color = 'k', linewidth = 1)
axes[1].set_ylabel('residuals')

plt.show()
irst solve with BASINHOPPING algorithm:
[[Fit Statistics]]
    # fitting method   = basinhopping
    # function evals   = 17238
    # data points      = 55
    # variables        = 3
    chi-square         = 51.0205702
    reduced chi-square = 0.98116481
    Akaike info crit   = 1.86926364
    Bayesian info crit = 7.89126320
[[Variables]]
    b0:  7.71901123 +/- 0.45562749 (5.90%) (init = 0)
    b1: -0.53569038 +/- 0.03472051 (6.48%) (init = 0)
    b2:  0.00118052 +/- 2.6156e-04 (22.16%) (init = 0)
[[Correlations]] (unreported correlations are < 0.100)
    C(b0, b2) = 0.912
    C(b0, b1) = 0.550
    C(b1, b2) = 0.242

second solve with BRUTE algorithm using the BASINHOPPING solution as a starting point:
[[Fit Statistics]]
    # fitting method   = brute
    # function evals   = 28830
    # data points      = 55
    # variables        = 3
    chi-square         = 51.0205702
    reduced chi-square = 0.98116481
    Akaike info crit   = 1.86926364
    Bayesian info crit = 7.89126320
##  Warning: uncertainties could not be estimated:
[[Variables]]
    b0:  7.71901123 +/- 0.45562749 (5.90%) (init = 0)
    b1: -0.53569038 +/- 0.03472051 (6.48%) (init = 0)
    b2:  0.00118052 +/- 2.6156e-04 (22.16%) (init = 0)
[[Correlations]] (unreported correlations are < 0.100)
    C(b0, b2) = 0.912
    C(b0, b1) = 0.550
    C(b1, b2) = 0.242
       99.73%    _BEST_    99.73%
 b0:  -3.89422   7.71901  +1.37162
 b1:  -0.20046  -0.53569  +0.12587
 b2:  -0.00096   0.00118  +0.00149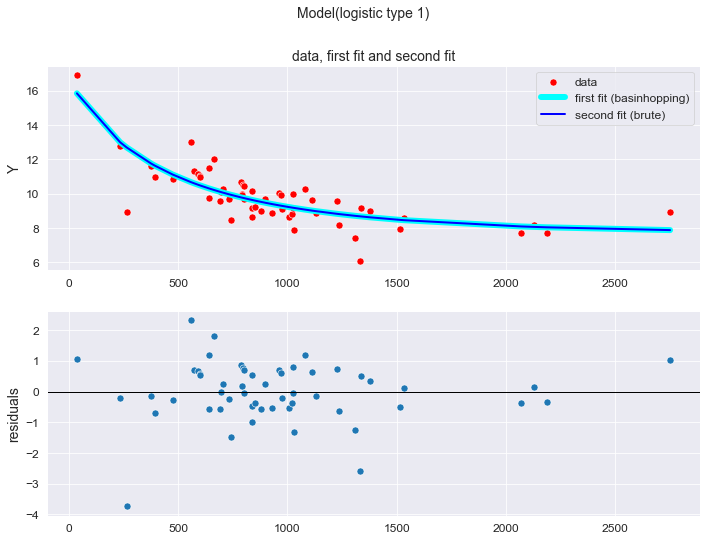

Пример 8 - обнаружение выбросов (outlier detection) при аппроксимации

Влияние выбросов на результаты аппроксимации может быть весьма существенным и игнорировать это влияние нельзя. Не будем сейчас сильно углубляться в этот вопрос, это предмет для отдельного рассмотрения, а просто проиллюстрируем прием выявления выбросов методом исключения (см. https://lmfit.github.io/lmfit-py/examples/example_detect_outliers.html#sphx-glr-examples-example-detect-outliers-py). Этот метод очень прост и заключается в следующем: будем последовательно исключать точки (x_i, y_i) из набора исходных данных, строить модель и анализировать, как влияет исключение точки на результат аппроксимации.

В качестве исходных данных рассмотрим зависимость расхода топлива (FuelFlow) от среднемесячной температуры (Temperature) из нашего датасета:

graph_scatterplot_sns(
    X2, Y,
    Xmin=X2_min_graph, Xmax=X2_max_graph,
    Ymin=Y_min_graph, Ymax=Y_max_graph,
    color='orange',
    title_figure=Title_String, title_figure_fontsize=14,
    title_axes='Dependence of FuelFlow (Y) on temperature (X2)', title_axes_fontsize=16,
    x_label=Variable_Name_X2,
    y_label=Variable_Name_Y,
    label_fontsize=14, tick_fontsize=12,
    label_legend='', label_legend_fontsize=12,
    s=80)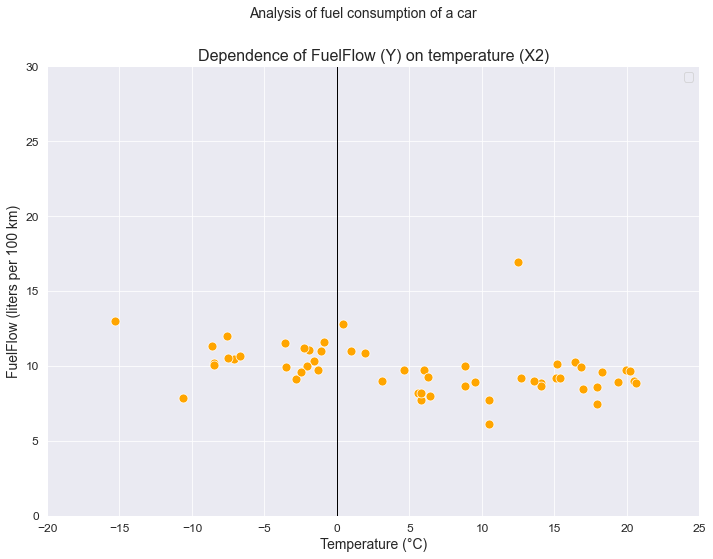

Подготовим исходные данные:

# Preparation of input data
dataset_sort_df = dataset_df.loc[:, ['X2', 'Y']].sort_values(by=['X2'])
display(dataset_sort_df.describe())

Y_sort = np.array(dataset_sort_df['Y'])
X_sort = np.array(dataset_sort_df['X2'])

Построим линейную модель:

# LINEAR MODEL
func_name = 'linear'
print(f'{func_name.upper()} MODEL: {formulas_dict[func_name]}')

func = models_dict[func_name]
p0 = p0_dict[func_name]

model = lmfit.Model(func,   
                    independent_vars=['x'],
                    name=func_name)

params = lmfit.Parameters()
params.add('b0', value=p0[0], min=-inf, max=inf)
params.add('b1', value=p0[1], min=-inf, max=inf)

result = model.fit(Y_sort, params, x=X_sort,
                   method='leastsq',
                   nan_policy='raise')

print(f'result.fit_report:\n{result.fit_report(min_correl=0.2)}\n')
dely = result.eval_uncertainty(sigma=3)

# graphic (data, best-fit, uncertainty band and residuals)
fig, axes = plt.subplots(2, 1, figsize=(297/INCH, 210/INCH))
fig.suptitle(f'Model({func_name})', fontsize=16)

axes[0].set_title('data, init-fit, best-fit, and uncertainty band')
sns.scatterplot(x=X_sort, y=Y_sort, label='data', s=50, color='red', ax=axes[0])
R2 = round(result.rsquared, DecPlace)
sns.lineplot(x=X_sort, y=result.best_fit, color='blue', linewidth=2, legend=True, label='best fit (' + r'$R^2 = $' + f'{R2})', ax=axes[0])
axes[0].fill_between(X_sort, result.best_fit-dely, result.best_fit+dely, color="grey", alpha=0.3, label=r'3-$\sigma$ band')
axes[0].legend()
axes[0].set_ylabel('Y')
#axes[0].set_xlim(X1_min_graph, X1_max_graph)
axes[0].set_ylim(Y_min_graph, Y_max_graph)

sns.scatterplot(x=X_sort, y=-result.residual, ax=axes[1], s=50)
axes[1].axhline(y = 0, color = 'k', linewidth = 1)
axes[1].set_xlabel('X')
axes[1].set_ylabel('residuals')
#axes[1].set_xlim(X1_min_graph, X1_max_graph)
#axes[1].set_ylim(Y_min_graph, Y_max_graph)

plt.show()
LINEAR MODEL: y = b0 + b1*x
result.fit_report:
[[Model]]
    Model(linear)
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 7
    # data points      = 55
    # variables        = 2
    chi-square         = 126.256130
    reduced chi-square = 2.38219113
    Akaike info crit   = 49.7038688
    Bayesian info crit = 53.7185352
    R-squared          = 0.13645691
[[Variables]]
    b0:  10.1218956 +/- 0.23996519 (2.37%) (init = 0)
    b1: -0.06161458 +/- 0.02129069 (34.55%) (init = 0)
[[Correlations]] (unreported correlations are < 0.200)
    C(b0, b1) = -0.498

График влияния на метрику качества аппроксимации - reduced chi-square

{\chi}_y^2 = \frac{\chi^2}{N-N_{varys}}:

from collections import defaultdict

best_vals = defaultdict(lambda: np.zeros(X_sort.size))
stderrs = defaultdict(lambda: np.zeros(X_sort.size))
chi_sq = np.zeros_like(X_sort)

for i in range(X_sort.size):
    idx2 = np.arange(0, X_sort.size)
    idx2 = np.delete(idx2, i)
    tmp_x = X_sort[idx2]
    tmp = model.fit(Y_sort[idx2], x=tmp_x, b0=result.params['b0'], b1=result.params['b1'])
    
    chi_sq[i] = tmp.chisqr
    for p in tmp.params:
        tpar = tmp.params[p]
        best_vals[p][i] = tpar.value
        stderrs[p][i] = (tpar.stderr / result.params[p].stderr)

fig, ax = plt.subplots(figsize=(297/INCH, 210/INCH))
ax.plot(X_sort, (result.chisqr - chi_sq) / chi_sq)
ax.set_ylabel(r'Relative red. $\chi^2$ change')
ax.set_xlabel('X')
ax.legend()
plt.show()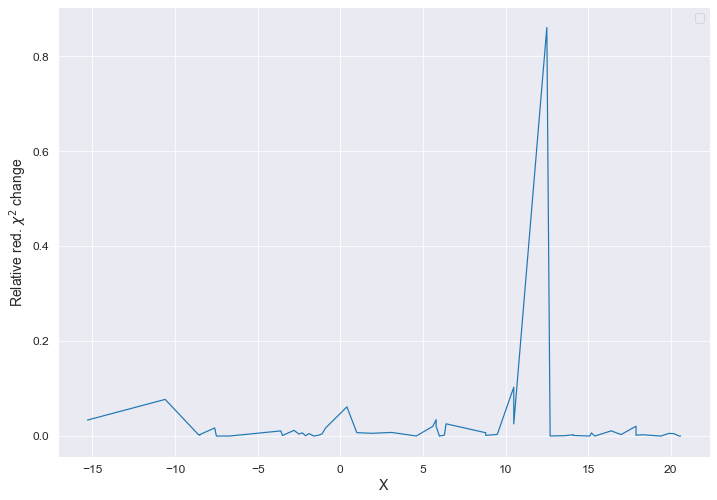

График влияния на значения параметров b_0, b_1 и их ошибки:

fig, axs = plt.subplots(4, figsize=(297/INCH, 210/INCH*3), sharex='col')
axs[0].plot(X_sort, best_vals['b0'])
axs[0].set_ylabel('best b0')

axs[1].plot(X_sort, best_vals['b1'])
axs[1].set_ylabel('best b1')

axs[2].plot(X_sort, stderrs['b0'])
axs[2].set_ylabel('err b0 change')

axs[3].plot(X_sort, stderrs['b1'])
axs[3].set_ylabel('err b1 change')

axs[3].set_xlabel('X')
plt.show()

Видим, что выброс y в интервале x\in(10; 15) очень хорошо заметен на всех графиках.
Наконец, исключим выброс и построим линейную модель по очищенным данным:

mask = dataset_sort_df['Y'] < 15
dataset_sort_df_clear = dataset_sort_df[mask]
display(dataset_sort_df_clear.describe())

X_sort_clear = np.array(dataset_sort_df_clear['X2'])
Y_sort_clear = np.array(dataset_sort_df_clear['Y'])
# LINEAR MODEL
func_name = 'linear'
print(f'{func_name.upper()} MODEL: {formulas_dict[func_name]}')

func = models_dict[func_name]
p0 = p0_dict[func_name]

model = lmfit.Model(func,   
                    independent_vars=['x'],
                    name=func_name)

params = lmfit.Parameters()
params.add('b0', value=p0[0], min=-inf, max=inf)
params.add('b1', value=p0[1], min=-inf, max=inf)

result = model.fit(Y_sort_clear, params, x=X_sort_clear,
                   method='leastsq',
                   nan_policy='raise')

print(f'result.fit_report:\n{result.fit_report(min_correl=0.2)}\n')
dely = result.eval_uncertainty(sigma=3)

# graphic (data, best-fit, uncertainty band and residuals)
fig, axes = plt.subplots(2, 1, figsize=(297/INCH, 210/INCH))
fig.suptitle(f'Model({func_name})', fontsize=16)

axes[0].set_title('data, init-fit, best-fit, and uncertainty band')
sns.scatterplot(x=X_sort_clear, y=Y_sort_clear, label='data', s=50, color='red', ax=axes[0])
R2 = round(result.rsquared, DecPlace)
sns.lineplot(x=X_sort_clear, y=result.best_fit, color='blue', linewidth=2, legend=True, label='best fit (' + r'$R^2 = $' + f'{R2})', ax=axes[0])
axes[0].fill_between(X_sort_clear, result.best_fit-dely, result.best_fit+dely, color="grey", alpha=0.3, label=r'3-$\sigma$ band')
axes[0].legend()
axes[0].set_ylabel('Y')
#axes[0].set_xlim(X1_min_graph, X1_max_graph)
axes[0].set_ylim(Y_min_graph, Y_max_graph)

sns.scatterplot(x=X_sort_clear, y=-result.residual, ax=axes[1], s=50)
axes[1].axhline(y = 0, color = 'k', linewidth = 1)
axes[1].set_xlabel('X')
axes[1].set_ylabel('residuals')
#axes[1].set_xlim(X1_min_graph, X1_max_graph)
#axes[1].set_ylim(Y_min_graph, Y_max_graph)

plt.show()
LINEAR MODEL: y = b0 + b1*x
result.fit_report:
[[Model]]
    Model(linear)
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 7
    # data points      = 54
    # variables        = 2
    chi-square         = 67.8407274
    reduced chi-square = 1.30462937
    Akaike info crit   = 16.3216480
    Bayesian info crit = 20.2996161
    R-squared          = 0.28334888
[[Variables]]
    b0:  10.0379989 +/- 0.17802593 (1.77%) (init = 0)
    b1: -0.07177285 +/- 0.01582893 (22.05%) (init = 0)
[[Correlations]] (unreported correlations are < 0.200)
    C(b0, b1) = -0.488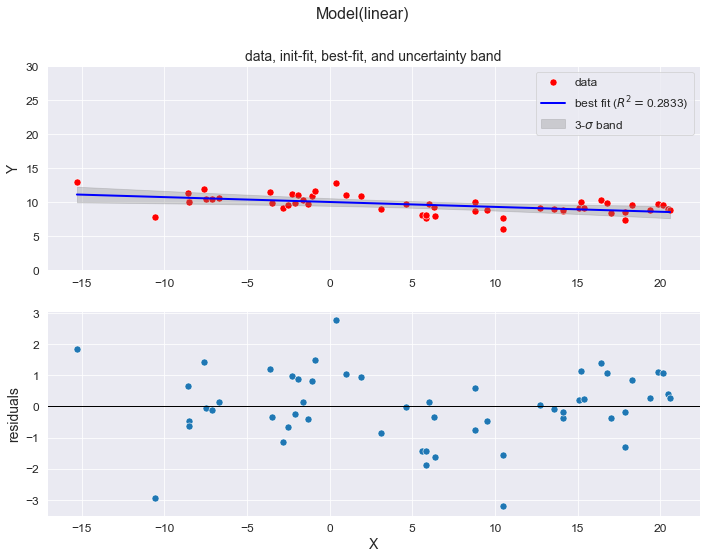

Видим, что исключение выброса позволило улучшить качество аппроксимации с R^2 = 0.1365 до R^2 = 0.2833.

Сравнительный анализ инструментов аппроксимации

Очевидно, что библиотека lmfit является наиболее совершенным инструментом аппроксимации в python, но и в то же время - наиболее сложным в освоении. Для более простых задач вполне может использоваться scipy.optimize.curve_fit.

Про быстродействие различных инструментов аппроксимации - см., например, https://mmas.github.io/least-squares-fitting-numpy-scipy.

В общем, каждый исследователь вправе сам выбирать инструменты для решения своих задач.

СОЗДАНИЕ ПОЛЬЗОВАТЕЛЬСКОЙ ФУНКЦИИ ДЛЯ АППРОКСИМАЦИИ ЗАВИСИМОСТЕЙ

Создадим пользовательскую функцию simple_approximation, которая позволит выполнять простую аппроксимацию зависимостей (по аналогии с тем, как это реализовано в MS Excel), а именно:

  • работать с наиболее распространенными моделями аппроксимации (линейной, квадратической, кубической, степенной, экспоненциальной, логарифмической, гиперболической);

  • выполнять визуализацию, в том числе нескольких моделей на одном графике;

  • выводить на графике уравнение моделей;

  • выводить на графике основные метрики качества моделей (R^2, MSPE, MAPE);

  • выводить числовые значения параметров моделей и метрик качества в виде DataFrame;

  • выводить значения Y, рассчитанные по моделям, в виде DataFrame.

Разумеется, данная функция не претендует на абсолютную полноту, она предназначена только лишь для облегчения предварительных исследований. В случае необходимости расширить набор моделей и/или выводимых данных, любой исследователь сможет получить необходимый результат по аналогии с тем, как это было продемонстрировано в примерах расчетов выше.

Функция simple_approximation имеет следующие параметры:

  • X_in, Y_in - исходные значения переменных X и Y;

  • models_list_in - список моделей для аппроксимации (например, полный перечень models_list = ['linear', 'quadratic', 'qubic', 'power', 'exponential', 'logarithmic', 'hyperbolic']);

  • p0_dict_in=None - словарь (dict) с начальными значениями параметров (по умолчанию равны 1);

  • Xmin, Xmax, Ymin, Ymax - границы значений для построения графиков;

  • nx_in=100 - число точек, на которое разбивается область значений переменной X для построения графиков;

  • DecPlace=4 - точность (число знаков после запятой) выводимых значений параметров и метрик качества моделей;

  • result_table=False, value_table_calc=False, value_table_graph=False - выводить или нет (True/False) DataFrame с параметрами моделей и метриками качества, с расчетными значениями переменной Y, с расчетными значениями переменной Y для графиков;

  • title_figure=None, title_figure_fontsize=16, title_axes=None, title_axes_fontsize=18 - заголовки и шрифт заголовков графиков;

  • x_label=None, y_label=None - наименования осей графиков;

  • linewidth=2 - толщина линий графиков;

  • label_fontsize=14, tick_fontsize=12, label_legend_fontsize=12 - заголовки и шрифт легенды;

  • color_list_in=None - словарь (dict), задающий цвета для графиков различных моделей (по умолчанию используется заданный в функции);

  • b0_formatter=None, b1_formatter=None, b2_formatter=None, b3_formatter=None - числовой формат для отображения параметров моделей (по умолчанию используется заданный в функции);

  • graph_size=(420/INCH, 297/INCH) - размер окна графиков;

  • file_name=None - имя файла для сохранения графика на диске.

Функция simple_approximation возвращает:

  • result_df - DataFrame с параметрами моделей и метриками качества;

  • value_table_calc и value_table_graph - DataFrame с расчетными значениями переменной Y, с расчетными значениями переменной Y для графиков;

  • выводит график аппроксимации.

def simple_approximation(
    X_in, Y_in,
    models_list_in,
    p0_dict_in=None,
    Xmin=None, Xmax=None,
    Ymin=None, Ymax=None,
    nx_in=100,
    DecPlace=4,
    result_table=False, value_table_calc=False, value_table_graph=False,
    title_figure=None, title_figure_fontsize=16,
    title_axes=None, title_axes_fontsize=18,
    x_label=None, y_label=None,
    linewidth=2,
    label_fontsize=14, tick_fontsize=12, label_legend_fontsize=12,
    color_list_in=None,
    b0_formatter=None, b1_formatter=None, b2_formatter=None, b3_formatter=None,
    graph_size=(420/INCH, 297/INCH),
    file_name=None):
    
    # Equations
    linear_func = lambda x, b0, b1: b0 + b1*x
    quadratic_func = lambda x, b0, b1, b2: b0 + b1*x + b2*x**2
    qubic_func = lambda x, b0, b1, b2, b3: b0 + b1*x + b2*x**2 + b3*x**3
    power_func = lambda x, b0, b1: b0 * x**b1
    exponential_func = lambda x, b0, b1: b0 * np.exp(b1*x)
    logarithmic_func = lambda x, b0, b1: b0 + b1*np.log(x)
    hyperbolic_func = lambda x, b0, b1: b0 + b1/x
    
    # Model reference
    p0_dict = {
        'linear':      [1, 1],
        'quadratic':   [1, 1, 1],
        'qubic':       [1, 1, 1, 1],
        'power':       [1, 1],
        'exponential': [1, 1],
        'logarithmic': [1, 1],
        'hyperbolic':  [1, 1]}
    
    models_dict = {
        'linear':      [linear_func,      p0_dict['linear']],
        'quadratic':   [quadratic_func,   p0_dict['quadratic']],
        'qubic':       [qubic_func,       p0_dict['qubic']],
        'power':       [power_func,       p0_dict['power']],
        'exponential': [exponential_func, p0_dict['exponential']],
        'logarithmic': [logarithmic_func, p0_dict['logarithmic']],
        'hyperbolic':  [hyperbolic_func,  p0_dict['hyperbolic']]}
    
    models_df = pd.DataFrame({
        'func': (
            linear_func,
            quadratic_func,
            qubic_func,
            power_func,
            exponential_func,
            logarithmic_func,
            hyperbolic_func),
        'p0': (
            p0_dict['linear'],
            p0_dict['quadratic'],
            p0_dict['qubic'],
            p0_dict['power'],
            p0_dict['exponential'],
            p0_dict['logarithmic'],
            p0_dict['hyperbolic'])},
        index=['linear', 'quadratic', 'qubic', 'power', 'exponential', 'logarithmic', 'hyperbolic'])
        
    models_dict_keys_list = list(models_dict.keys())
    models_dict_values_list = list(models_dict.values())
        
    # Initial guess for the parameters
    if p0_dict_in:
        p0_dict_in_keys_list = list(p0_dict_in.keys())
        for elem in models_dict_keys_list:
            if elem in p0_dict_in_keys_list:
                models_dict[elem][1] = p0_dict_in[elem]
            
    # Calculations
    X_fact = np.array(X_in)
    Y_fact = np.array(Y_in)
    
    nx = 100 if not(nx_in) else nx_in
    hx = (Xmax - Xmin)/(nx - 1)
    X_calc_graph = np.linspace(Xmin, Xmax, nx)
    
    parameters_list = list()
    models_list = list()
    
    error_metrics_df = pd.DataFrame(columns=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE', 'R2'])
    Y_calc_graph_df = pd.DataFrame({'X': X_calc_graph})
    Y_calc_df = pd.DataFrame({
        'X_fact': X_fact,
        'Y_fact': Y_fact})
    
    for elem in models_list_in:
        if elem in models_dict_keys_list:
            func = models_dict[elem][0]
            p0 = models_dict[elem][1]
            popt_, _ = curve_fit(func, X_fact, Y_fact, p0=p0)
            models_dict[elem].append(popt_)
            Y_calc_graph = func(X_calc_graph, *popt_)
            Y_calc = func(X_fact, *popt_)
            Y_calc_graph_df[elem] = Y_calc_graph
            Y_calc_df[elem] = Y_calc
            parameters_list.append(popt_)
            models_list.append(elem)
            (model_error_metrics, result_error_metrics) = regression_error_metrics(Yfact=Y_fact, Ycalc=Y_calc_df[elem], model_name=elem)
            error_metrics_df = pd.concat([error_metrics_df, result_error_metrics])
                
    parameters_df = pd.DataFrame(parameters_list,
                                 index=models_list)
    parameters_df = parameters_df.add_prefix('b')
    result_df = parameters_df.join(error_metrics_df)
                        
    # Legend for a linear model
    if "linear" in models_list_in:
        b0_linear = round(result_df.loc["linear", "b0"], DecPlace)
        b0_linear_str = str(b0_linear)
        b1_linear = round(result_df.loc["linear", "b1"], DecPlace)
        b1_linear_str = f' + {b1_linear}' if b1_linear > 0 else f' - {abs(b1_linear)}'
        R2_linear = round(result_df.loc["linear", "R2"], DecPlace)
        MSPE_linear = result_df.loc["linear", "MSPE"]
        MAPE_linear = result_df.loc["linear", "MAPE"]
        label_linear = 'linear: ' + r'$Y_{calc} = $' + b0_linear_str + b1_linear_str + f'{chr(183)}X' + ' ' + \
            r'$(R^2 = $' + f'{R2_linear}' + ', ' + f'MSPE = {MSPE_linear}' + ', ' + f'MAPE = {MAPE_linear})'
    
    # Legend for a quadratic model
    if "quadratic" in models_list_in:
        b0_quadratic = round(result_df.loc["quadratic", "b0"], DecPlace)
        b0_quadratic_str = str(b0_quadratic)
        b1_quadratic = result_df.loc["quadratic", "b1"]
        b1_quadratic_str = f' + {b1_quadratic:.{DecPlace}e}' if b1_quadratic > 0 else f' - {abs(b1_quadratic):.{DecPlace}e}'
        b2_quadratic = result_df.loc["quadratic", "b2"]
        b2_quadratic_str = f' + {b2_quadratic:.{DecPlace}e}' if b2_quadratic > 0 else f' - {abs(b2_quadratic):.{DecPlace}e}'
        R2_quadratic = round(result_df.loc["quadratic", "R2"], DecPlace)
        MSPE_quadratic = result_df.loc["quadratic", "MSPE"]
        MAPE_quadratic = result_df.loc["quadratic", "MAPE"]
        label_quadratic = 'quadratic: ' + r'$Y_{calc} = $' + b0_quadratic_str + b1_quadratic_str + f'{chr(183)}X' + b2_quadratic_str + f'{chr(183)}' + r'$X^2$' + ' ' + \
            r'$(R^2 = $' + f'{R2_quadratic}' + ', ' + f'MSPE = {MSPE_quadratic}' + ', ' + f'MAPE = {MAPE_quadratic})'
    
    # Legend for a qubic model
    if "qubic" in models_list_in:
        b0_qubic = round(result_df.loc["qubic", "b0"], DecPlace)
        b0_qubic_str = str(b0_qubic)
        b1_qubic = result_df.loc["qubic", "b1"]
        b1_qubic_str = f' + {b1_qubic:.{DecPlace}e}' if b1_qubic > 0 else f' - {abs(b1_qubic):.{DecPlace}e}'
        b2_qubic = result_df.loc["qubic", "b2"]
        b2_qubic_str = f' + {b2_qubic:.{DecPlace}e}' if b2_qubic > 0 else f' - {abs(b2_qubic):.{DecPlace}e}'
        b3_qubic = result_df.loc["qubic", "b3"]
        b3_qubic_str = f' + {b3_qubic:.{DecPlace}e}' if b3_qubic > 0 else f' - {abs(b3_qubic):.{DecPlace}e}'
        R2_qubic = round(result_df.loc["qubic", "R2"], DecPlace)
        MSPE_qubic = result_df.loc["qubic", "MSPE"]
        MAPE_qubic = result_df.loc["qubic", "MAPE"]
        label_qubic = 'qubic: ' + r'$Y_{calc} = $' + b0_qubic_str + b1_qubic_str + f'{chr(183)}X' + \
            b2_qubic_str + f'{chr(183)}' + r'$X^2$' + b3_qubic_str + f'{chr(183)}' + r'$X^3$' + ' ' + \
            r'$(R^2 = $' + f'{R2_qubic}' + ', ' + f'MSPE = {MSPE_qubic}' + ', ' + f'MAPE = {MAPE_qubic})'
    
    # Legend for a power model
    if "power" in models_list_in:
        b0_power = round(result_df.loc["power", "b0"], DecPlace)
        b0_power_str = str(b0_power)
        b1_power = round(result_df.loc["power", "b1"], DecPlace)
        b1_power_str = str(b1_power)
        R2_power = round(result_df.loc["power", "R2"], DecPlace)
        MSPE_power = result_df.loc["power", "MSPE"]
        MAPE_power = result_df.loc["power", "MAPE"]
        label_power = 'power: ' + r'$Y_{calc} = $' + b0_power_str + f'{chr(183)}' + r'$X$'
        for elem in b1_power_str:
            label_power = label_power + r'$^{}$'.format(elem)
        label_power = label_power  + ' ' + r'$(R^2 = $' + f'{R2_power}' + ', ' + f'MSPE = {MSPE_power}' + ', ' + f'MAPE = {MAPE_power})'
    
    # Legend for a exponential model
    if "exponential" in models_list_in:
        b0_exponential = round(result_df.loc["exponential", "b0"], DecPlace)
        b0_exponential_str = str(b0_exponential)
        b1_exponential = result_df.loc["exponential", "b1"]
        b1_exponential_str = f'{b1_exponential:.{DecPlace}e}'
        R2_exponential = round(result_df.loc["exponential", "R2"], DecPlace)
        MSPE_exponential = result_df.loc["exponential", "MSPE"]
        MAPE_exponential = result_df.loc["exponential", "MAPE"]
        label_exponential = 'exponential: ' + r'$Y_{calc} = $' + b0_exponential_str + f'{chr(183)}' + r'$e$'
        for elem in b1_exponential_str:
            label_exponential = label_exponential + r'$^{}$'.format(elem)
        label_exponential = label_exponential + r'$^{}$'.format(chr(183)) + r'$^X$' + ' ' + \
            r'$(R^2 = $' + f'{R2_exponential}' + ', ' + f'MSPE = {MSPE_exponential}' + ', ' + f'MAPE = {MAPE_exponential})'
    
    # Legend for a logarithmic model
    if "logarithmic" in models_list_in:
        b0_logarithmic = round(result_df.loc["logarithmic", "b0"], DecPlace)
        b0_logarithmic_str = str(b0_logarithmic)
        b1_logarithmic = round(result_df.loc["logarithmic", "b1"], DecPlace)
        b1_logarithmic_str = f' + {b1_logarithmic}' if b1_logarithmic > 0 else f' - {abs(b1_logarithmic)}'
        R2_logarithmic = round(result_df.loc["logarithmic", "R2"], DecPlace)
        MSPE_logarithmic = result_df.loc["logarithmic", "MSPE"]
        MAPE_logarithmic = result_df.loc["logarithmic", "MAPE"]
        label_logarithmic = 'logarithmic: ' + r'$Y_{calc} = $' + b0_logarithmic_str + b1_logarithmic_str + f'{chr(183)}ln(X)' + ' ' + \
            r'$(R^2 = $' + f'{R2_logarithmic}' + ', ' + f'MSPE = {MSPE_logarithmic}' + ', ' + f'MAPE = {MAPE_logarithmic})'
    
    # Legend for a hyperbolic model
    if "hyperbolic" in models_list_in:
        b0_hyperbolic = round(result_df.loc["hyperbolic", "b0"], DecPlace)
        b0_hyperbolic_str = str(b0_hyperbolic)
        b1_hyperbolic = round(result_df.loc["hyperbolic", "b1"], DecPlace)
        b1_hyperbolic_str = f' + {b1_hyperbolic}' if b1_hyperbolic > 0 else f' - {abs(b1_hyperbolic)}'
        R2_hyperbolic = round(result_df.loc["hyperbolic", "R2"], DecPlace)
        MSPE_hyperbolic = result_df.loc["hyperbolic", "MSPE"]
        MAPE_hyperbolic = result_df.loc["hyperbolic", "MAPE"]
        label_hyperbolic = 'hyperbolic: ' + r'$Y_{calc} = $' + b0_hyperbolic_str + b1_hyperbolic_str + f' / X' + ' ' + \
            r'$(R^2 = $' + f'{R2_hyperbolic}' + ', ' + f'MSPE = {MSPE_hyperbolic}' + ', ' + f'MAPE = {MAPE_hyperbolic})'
        
    # Legends
    label_legend_dict = {
        'linear':      label_linear if "linear" in models_list_in else '',
        'quadratic':   label_quadratic if "quadratic" in models_list_in else '',
        'qubic':       label_qubic if "qubic" in models_list_in else '',
        'power':       label_power if "power" in models_list_in else '',
        'exponential': label_exponential if "exponential" in models_list_in else '',
        'logarithmic': label_logarithmic if "logarithmic" in models_list_in else '',
        'hyperbolic':  label_hyperbolic if "hyperbolic" in models_list_in else ''}
    
    # Graphics
    color_dict = {
        'linear':      'blue',
        'quadratic':   'green',
        'qubic':       'brown',
        'power':       'magenta',
        'exponential': 'cyan',
        'logarithmic': 'orange',
        'hyperbolic':  'grey'}
    
    if not(Xmin) and not(Xmax):
        Xmin = min(X_fact)*0.99
        Xmax = max(X_fact)*1.01
    if not(Ymin) and not(Ymax):
        Ymin = min(Y_fact)*0.99
        Ymax = max(Y_fact)*1.01     
        
    fig, axes = plt.subplots(figsize=(graph_size))
    fig.suptitle(title_figure, fontsize = title_figure_fontsize)
    axes.set_title(title_axes, fontsize = title_axes_fontsize)
    
    sns.scatterplot(
        x=X_fact, y=Y_fact,
        label='data',
        s=50,
        color='red',
        ax=axes)
       
    for elem in models_list_in:
        if elem in models_dict_keys_list:
            sns.lineplot(
                x=X_calc_graph, y=Y_calc_graph_df[elem],
                color=color_dict[elem],
                linewidth=linewidth,
                legend=True,
                label=label_legend_dict[elem],
                ax=axes)

    axes.set_xlim(Xmin, Xmax)
    axes.set_ylim(Ymin, Ymax)
    axes.set_xlabel(x_label, fontsize = label_fontsize)
    axes.set_ylabel(y_label, fontsize = label_fontsize)
    axes.tick_params(labelsize = tick_fontsize)
    axes.legend(prop={'size': label_legend_fontsize})

    plt.show()
    
    if file_name:
        fig.savefig(file_name, orientation = "portrait", dpi = 300)
    
    # result output
    output_list = [result_df, Y_calc_df, Y_calc_graph_df]
    result_list = [result_table, value_table_calc, value_table_graph]
    result = list()
    for i, elem in enumerate(result_list):
        if elem:
            result.append(output_list[i])
    
    # result display
    for elem in ['MSPE', 'MAPE']:
        result_df[elem] = result_df[elem].apply(lambda s: float(s[:-1]))
    b_formatter = [b0_formatter, b1_formatter, b2_formatter, b3_formatter]
    if result_table:
        display(result_df
                .style
                    .format(
                        precision=DecPlace, na_rep='-',
                        formatter={
                            'b0': b0_formatter if b0_formatter else '{:.4f}',
                            'b1': b1_formatter if b1_formatter else '{:.4f}',
                            'b2': b2_formatter if b2_formatter else '{:.4e}',
                            'b3': b3_formatter if b3_formatter else '{:.4e}'})
                    .highlight_min(color='green', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE'])
                    .highlight_max(color='red', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE'])
                    .highlight_max(color='green', subset='R2')
                    .highlight_min(color='red', subset='R2')
                    .applymap(lambda x: 'color: orange;' if abs(x) <= 10**(-(DecPlace-1)) else None, subset=parameters_df.columns))
    
    if value_table_calc:
        display(Y_calc_df)
    if value_table_graph:
        display(Y_calc_graph_df)
                    
    return result

Выполним аппроксимацию зависимости среднемесячного расхода топлива автомобиля (л/100 км) (FuelFlow) от среднемесячного пробега (км) (Mileage):

title_figure = Title_String + '\n' + Task_Theme + '\n'
title_axes = 'Fuel mileage ratio'
    
models_list = ['linear', 'power', 'exponential', 'quadratic', 'qubic', 'logistic', 'logarithmic', 'hyperbolic']

p0_dict_in= {'exponential': [1, -0.1],
             'power': [1, -0.1]}

(result_df,
value_table_calc,
value_table_graph
) = simple_approximation(
    X1, Y,
    models_list, p0_dict_in,
    Xmin = X1_min_graph, Xmax = X1_max_graph,
    Ymin = Y_min_graph, Ymax = Y_max_graph,
    DecPlace=DecPlace,
    result_table=True, value_table_calc=True, value_table_graph=True,
    title_figure = title_figure,
    title_axes = title_axes,
    x_label=Variable_Name_X1,
    y_label=Variable_Name_Y,
    linewidth=2,
    b1_formatter='{:.' + str(DecPlace + 3) + 'f}', b2_formatter='{:.' + str(DecPlace) + 'e}', b3_formatter='{:.' + str(DecPlace) + 'e}')

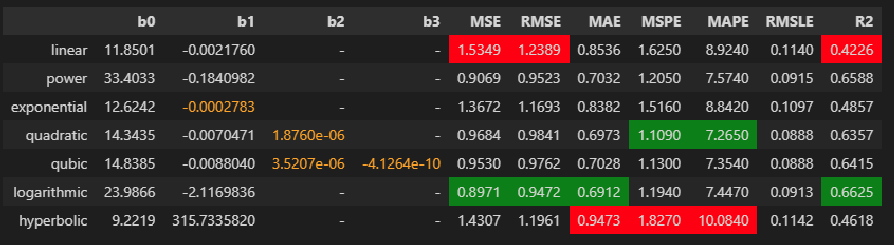
Выполним аппроксимацию зависимости среднемесячного расхода топлива автомобиля (л/100 км) (FuelFlow) от срднемесячной температуры (Temperature):

models_list = ['linear', 'exponential', 'quadratic']

(result_df,
value_table_calc,
value_table_graph
) = simple_approximation(
    X_sort_clear, Y_sort_clear,
    models_list, p0_dict_in,
    Xmin = X2_min_graph, Xmax = X2_max_graph,
    Ymin = Y_min_graph, Ymax = Y_max_graph,
    DecPlace=DecPlace,
    result_table=True, value_table_calc=True, value_table_graph=True,
    title_figure = title_figure,
    title_axes = 'Dependence of FuelFlow on temperature',
    x_label=Variable_Name_X2,
    y_label=Variable_Name_Y,
    linewidth=2,
    b1_formatter='{:.' + str(DecPlace + 3) + 'f}', b2_formatter='{:.' + str(DecPlace) + 'e}', b3_formatter='{:.' + str(DecPlace) + 'e}')

Небольшой offtop - сравнение результатов расчетов с использованием различного программного обеспечения

Напоследок хочу привести данные сравнения результатов аппроксимации с помощью различных программных средств:

  • Python, функция scipy.optimize.curve_fit;

  • MS Excel;

  • система компьютерной алгебры Maxima (которую я настоятельно рекомендую освоить всем специалистам, выполняющим математические расчеты).

Все файлы с расчетами доступны в моем репозитории на GitHub (https://github.com/AANazarov/MyModulePython).

Итак:

Python, функция scipy.optimize.curve_fit:

Модель

Уравнение

Коэффициент R^2

линейная

Y=11.8501-2.1760 \cdot 10^{-3} \cdot X

0.4226

квадратическая

Y=14.3435-7.0471 \cdot 10^{-3} \cdot X+1.8760 \cdot 10^{-6} \cdot X^2

0.6357

кубическая

Y=14.8385-8.804 \cdot 10^{-3} \cdot X+3.5207 \cdot 10^{-6} \cdot X^2-4.1264 \cdot 10^{-10} \cdot X^3

0.6415

степенная

Y=33.4033\cdot X^{-0.1841}

0.6588

экспоненциальная I типа

Y=12.6242\cdot e^{2.783\cdot 10^{-4} \cdot X}

0.4857

экспоненциальная II типа

Y=12.6242\cdot 0.9997^X

0.4857

логарифмическая

Y=23.9866-2.1169\cdot ln X

0.6625

гиперболическая

Y=9.2219+\frac{315.7336}{X}

0.4618

MS Excel:

Модель

Уравнение

Коэффициент R^2

линейная

Y=11.85-0.0022 \cdot X

0.4226

квадратическая

Y=14.345-0.007 \cdot X+2 \cdot 10^{-6} \cdot X^2

0.6359

кубическая

Y=14.84-0.0088 \cdot X+4 \cdot 10^{-6} \cdot X^2-4 \cdot 10^{-10} \cdot X^3

0.6417

степенная

Y=35.303\cdot X^{-0.193}

0.6582

экспоненциальная I типа

Y=11.848\cdot e^{2\cdot 10^{-4} \cdot X}

0.4739

экспоненциальная II типа

-

-

логарифмическая

Y=23.989-2.117\cdot ln X

0.6627

гиперболическая

-

-

Maxima:

Модель

Уравнение

Коэффициент R^2

линейная

Y=11.85-2.1760 \cdot 10^{-3} \cdot X

0.4226

квадратическая

Y=14.343-7.0471 \cdot 10^{-3} \cdot X+1.8760 \cdot 10^{-6} \cdot X^2

0.6357

кубическая

Y=14.838-8.804 \cdot 10^{-3} \cdot X+3.5207 \cdot 10^{-6} \cdot X^2-4.1264 \cdot 10^{-10} \cdot X^3

0.6415

степенная

Y=33.355\cdot X^{-0.18388}

0.6588

экспоненциальная I типа

Y=12.624\cdot e^{2.7835\cdot 10^{-4} \cdot X}

0.4857

экспоненциальная II типа

Y=12.624\cdot 0.99972^X

0.4857

логарифмическая

Y=23.987-2.117\cdot ln X

0.6625

гиперболическая

Y=9.2219+\frac{315.73}{X}

0.4618

Как видим, результаты имеют незначительные отличия для степенных и экспоненциальных зависимостей. Есть над чем задуматься...

ИТОГИ

Итак, подведем итоги:

  • мы рассмотрели основные инструменты Python для аппроксимации зависимостей;

  • разобрали особенности определения ошибок и построения доверительных интервалов для параметров моделей аппроксимации;

  • также предложен пользовательская функция для аппроксимации простых зависимостей (по аналогии с тем, как это реализовано в Excel), облегчающая работу исследователя и уменьшающая размер программного кода.

Само собой, мы рассмотрели в рамках данного обзора далеко не все вопросы, связанные с аппроксимацией; так отдельного рассмотрения, безусловно, заслуживают следующие вопросы:

  • аппроксимация более сложных зависимостей (модифицированных кривых, S-образных кривых и пр.), требующих предварительной оценки начальных условий для алгоритма оптимизации;

  • влияние выбора алгоритма оптимизации на результат и быстройдействие;

  • аппроксимация с ограничениями в виде интервалов (bounds) и в виде алгебраических выражений (constraints);

  • более глубокое рассмотрение возможностей библиотеки lmfit для решения задач аппроксимации,

и т.д.

В общем, есть куда двигаться дальше.

Исходный код находится в моем репозитории на GitHub (https://github.com/AANazarov/Statistical-methods).

Надеюсь, данный обзор поможет специалистам DataScience в работе.

Комментарии (15)


  1. netcore7
    14.04.2023 07:38
    #25444750

    А что значит слово регрессия, откуда такой термин?


    1. ANazarov Автор
      14.04.2023 07:38
      #25444760

      Термин "регрессия" предложен еще в 19 в. Погуглите про историю статистики, информации море...


      1. netcore7
        14.04.2023 07:38
        #25444906

        погуглил - ничего не понял, причем тут снижение, что снижаеся то? У вас есть какое-то свое мнение на этот счет?


        1. ANazarov Автор
          14.04.2023 07:38
          #25444938
          +1

          Рекомендую список литературы для изучения основ теории:

          1. Айвазян С.А. Прикладная статистика. Основы эконометрики: В 2 т. - Т.2: Основы эконометрики. - 2-е изд., испр. - М.: ЮНИТИ-ДАНА, 2001. - 432 с.

          2. Вучков И. и др. Прикладной линейный регрессионный анализ / пер. с болг. - М.: Финансы и статистика, 1987. - 239 с.

          3. Фёрстер Э., Рёнц Б. Методы корреляционного и регрессионного анализа / пер с нем. - М.: Финансы и статистика, 1983. - 302 с.

          4. Львовский Е.Н. Статистические методы построения эмпирических формул. - М.: Высшая школа, 1988. - 239 с.


        1. CrazyElf
          14.04.2023 07:38
          #25445130

          Вот прямо в Википедии написано: "... Более интересным было то, что разброс в росте сыновей был меньшим, чем разброс в росте отцов. Так проявлялась тенденция возвращения роста сыновей к среднему (regression to mediocrity), то есть «регресс»." Вот это "возвращение к среднему" и есть суть регрессии. Дальше можно "Центральную предельную теорему" покурить, которая про тоже самое. В общем, грубо говоря, суть в том, что сумма случайных величин стремится к некоему усреднённому значению, на этом весь аппарат регрессии и стоит.


          1. netcore7
            14.04.2023 07:38
            #25445348
            +1

            что разброс в росте сыновей был меньшим,

            Видите в вашей же цитате - уменьшени кол-ва параметров! имхо мне кажется вы неверно поняли посыл регрессии - смысл, как мне кажется, в представлении исходной последовательности в виде генератора с минимальным кол-вом параметров с минимизированной по какому-то критерию ошибкой интерполяции.

            т.е. в пределе если все сыновья имели один рост - то этот набор данных можно представить одним параметром - просто числом. Ргресиия от N параметров (роста сыновей) к одному единственному их всех предтавляющему.


            1. CrazyElf
              14.04.2023 07:38
              #25446314

              Ну, наверное, можно и так сказать. По-моему суть одна и та же, просто я посмотрел с точки зрения распределений.


  1. CrazyElf
    14.04.2023 07:38
    #25445144

    Какой фундаментальный труд. Интересно, сколько примерно по времени этот проект занял. )


    1. ANazarov Автор
      14.04.2023 07:38
      #25445178

      Опыт работы за несколько лет - просто методически обобщен и скомпилирован. Так что на самом деле оформление не так и много времени заняло.


  1. thevlad
    14.04.2023 07:38
    #25445672

    Для чисто линейных многофакторных моделей, есть прекрасный scikit-learn, где есть регуляризация и различные cost function. Вообще если факторов относительно много то без регуляризации никуда, странно что вы об этом не написали.


    1. ANazarov Автор
      14.04.2023 07:38
      #25445810
      +2

      Я в этом обзоре писал не про машинное обучение, а про аппроксимацию, о простых (не многофакторных) моделях, причем в основном о нелинейных. scikit-learn - это отдельный инструмент. До него дело еще дойдет. А этот обзор совсем не про него.

      Нельзя объять необъятное


  1. uchitel
    14.04.2023 07:38
    #25446758

    Круть!


  1. sentimentaltrooper
    14.04.2023 07:38
    #25447088

    Добавил в закладки в надежде вернуться позже. По картинке превью сначала подумал, что рисовалось в ggplot2 в R. Есть ли какие-то преимущества перед ним? Или чисто что бы два синтаксиса не учить? Мне как-то показалось в R чуть больше готовых пакетов для работы с разными форматами нечисловых данных (все вот эти лютые timestamp который каждый лепит как хочет), отдельно нравится возможность сверстать всё в markdown, который почти совместим с внутренней wiki. Но все мои остальные разработчики сидят на питоне, так что я вот уже какое-то время чешу в затылке - не переучиться ли на него, но так как подобный анализ делам раз в несколько проектов, то мотивации не много.


    1. ANazarov Автор
      14.04.2023 07:38
      #25447322

      Хороший вопрос, коллега. В свое время с товарищем тоже спорили, за чаркой, что лучше - Python или R )) Если совсем кратко, я сделал выбор в пользу Python, хотя у R тоже свои плюсы есть. В общем тема для целой дискуссии...


    1. ANazarov Автор
      14.04.2023 07:38
      #25447326

      подобный анализ делам раз в несколько проектов

      Это даже не анализ, а так - демонстрация возможностей