Самообучающийся трекер объектов: как отслеживать цель в изменчивых условиях сцены / forpes.ru

Главная
Самообучающийся трекер объектов: как отслеживать цель в изменчивых условиях сцены

Самообучающийся трекер объектов: как отслеживать цель в изменчивых условиях сцены +12

16.09.2022 17:20

matkov 0 1900 Источник

Специалисты по компьютерному зрению не один десяток лет бьются над трекингом объектов. Они перепробовали многое: от старой-доброй оценки движения оптическим потоком до сетей-трансформеров.

Есть один подход к трекингу, широко известный на западе, но о котором мало пишут по-русски: Incremental Visual Tracker (IVT). Это трекер объектов на основе модифицированного метода главных компонент: он самообучается на ходу и адаптируется к изменчивым условиям.

Давайте исследуем физиологию этого трекера, чем он интересен и где его можно применить - а затем изучим проблемы его реализации и нюансы использования. Под катом ссылка на репозиторий и много математики.

Всем, кто интересуется исключительно реализацией, предъявляю C++-код. Есть также прототип на Python. Лицензии нету, делать можно что угодно.

О трекинге вкратце

Трекинг - это задача отслеживания объекта в сцене. Решается она путем предсказания местоположения объекта на последующем кадре с учетом динамики его движения. Трекинг применяется во многих задачах видеоаналитики среди которых наиболее выделяются подсчет посетителей, анализ поведения (например, животных на ферме или мышей в лабиринте), анализ траектории авто для вычисления средней скорости, отслеживание лица для определения лучшего кадра, подходящего для идентификации. Всего сценариев использования, естественно, гораздо больше.

Для интересующихся данной темой рекомендую подробную статью с примерами.

IVT трекер относится к классу так называемых appearance-based трекеров. Идея appearance-based подхода состоит в том, чтобы создать или обучить признаковое описание целевого объекта на начальном кадре и отслеживать его перемещение с помощью этого описания на последующих кадрах. Например, мы можем представить объект цветовой гистограммой и в дальнейшем искать регион с наиболее похожим цветовым распределением. Или обучить нейросеть представлять объект вектором эмбеддингов в евклидовом пространстве с тем свойством, что похожие объекты в этом пространстве будут находиться рядом, в то время как непохожие объекты далеко. Это был намек на DeepSORT. Альтернативный подход к трекингу, неформально - detection-based, не предполагает использования “внешнего вида” объекта и основывается исключительно на отслеживании его координат. Преимущество же кодирования “внешнего вида” объекта заключается в том, что эта информация вкупе с координатами объекта улучшает качество трекинга. Визуально разницу между detection-моделью и appearance-моделью можно увидеть на видео ниже.

Видео 1. На видео слева пример работы трекера SORT: зеленая рамка соответствует детектору YOLO, который выдает сработку раз в 3 кадра, красная рамка соответствует оценке фильтром Калмана между детекциями. На правом видео пример трекера IVT: красная рамка соответствует оценке на основе appearance-модели, без всякой детекции.

Далее мы рассмотрим все составляющие IVT трекера, сперва по отдельности, затем соединив все вместе.

Компактное представление объекта

Вместо того, чтобы работать с изображением объекта напрямую, как с набором независимых пикселей, разумнее описать его неким набором признаков, характеризующих этот объект. Так мы уменьшим размерность оставив только самую релевантную информацию об объекте. В качестве признакового описания объекта может быть использовано не только цветовое распределение, пример которого был приведен выше, но и его контур, текстура или более абстрактные признаки, такие как вектор эмбеддингов или базис главных компонент.

Мы будем представлять объект в (под)пространстве малой размерности - собственном базисе. Он же базис главных компонент, он же eigenbasis. Этот базис содержит бóльшую часть всей релевантной информации об объекте несмотря на то, что его размерность гораздо ниже исходной. Моделировать этот базис мы будем с помощью метода главных компонент (principal component analysis) используя первые изображений объекта на начальных кадрах.

Кратко напомню, что суть метода главных компонент состоит в том, чтобы найти для исходных данных такую систему координатных осей (главных компонент), которая давала бы наибольшую дисперсию расстояний между проекциями на эту систему. Проецируя исходный вектор данных $\vec v \in \mathbb{R}^d$ на новую систему мы получаем новый вектор ${\hat {\vec v}} \in \mathbb{R}^d$ , который мы можем урезать вплоть до ${\hat {\vec v}} \in \mathbb{R}^k$ , где оставшихся значений соответствуют осям наибольшей дисперсии.

На рисунках ниже приведены примеры уменьшения размерности.

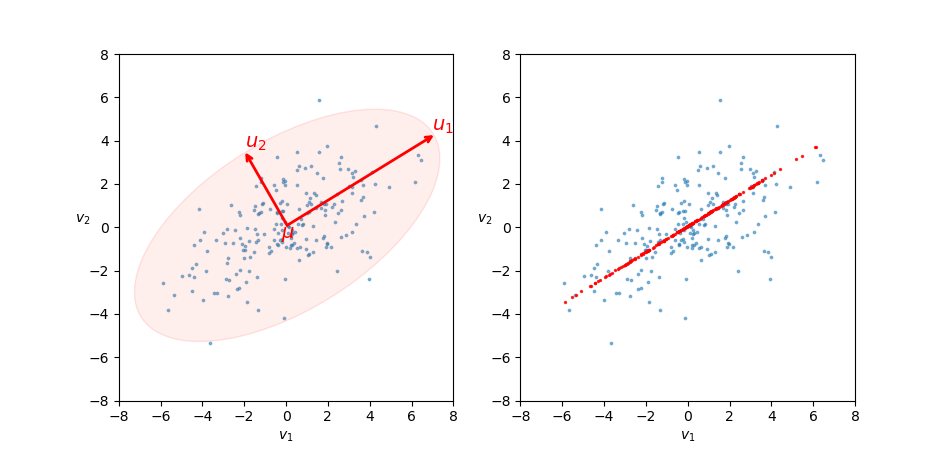
Рис. 1. Визуализация уменьшения размерности в двумерном пространстве. Исходные данные представляют собой массив векторов ${\vec v^{(i)}}\in\mathbb{R}^2$ , каждый из которых изображается точкой на графике с координатами $(v^{(i)}_1, v^{(i)}_2)$ . Рисунок слева иллюстрирует новую ортогональную систему координат ${U={\begin{bmatrix}\vec {u} _{1} \ \vec {u} _{2}\end{bmatrix}}}^T$ с центром в ${\vec \mu}$ . Рисунок справа иллюстрирует проекцию исходных данных (красные точки) на систему, состоящую только из первой главной компоненты $\vec u_1$ . Так как разброс проекций для оси $\vec u_2$ заметно меньше разброса оси $\vec u_1$ , мы можем отсечь вторую ось, пожертвовать некоторой информацией, сохранив при этом основную. Таким образом проекция ${\hat{\vec v}}\in\mathbb{R}^1$ представляется одним числом и мы сократили размерность с 2 до 1.

Рис. 2. Красивая анимация поиска оси с наибольшей дисперсией. Источник https://builtin.com/data-science/step-step-explanation-principal-component-analysis.

Весь аппарат, проиллюстрированный на рисунках 1 и 2 для двумерного случая будет также справедлив для пространства любой размерности. Так как исходными данными в нашем случае является одноканальное изображение объекта $I\in\mathbb{R}^{w\times h}$ или $I\in\mathbb{R}^{d=wh}$ , вырезанное из оригинального кадра, то мы будем считать, что проекция на базис $U\in\mathbb{R}^{k\times k}$ , где ${k}\ll{d}$ , представляет собой вектор признаков ${\hat I}\in\mathbb{R}^{k}$ этого объекта. В программной реализации, о которой будет рассказано ниже, будут использованы первые 16 главных компонент при исходной длине вектора 32x32=1024. Согласимся, что оперировать матрицами $U\in\mathbb{R}^{16\times 16}$ гораздо выгоднее чем матрицами $U\in\mathbb{R}^{1024\times 1024}$ . На рисунке ниже визуально представлены первые четыре главные компоненты для изображений велосипеда.

Рис. 3. Визуализация первых главных компонент для пятидесяти изображений велосипеда. Слева-направо: оригинальный кадр, среднее по последним пятидесяти кадрам, главные компоненты с первой по четвертую.

Ранее мы говорили, что appearance-based подход предполагает отслеживание объекта на последующих кадрах с помощью признакового описания объекта. Каким же образом признаковое описание в пространстве главных компонент может быть использовано нами для отслеживания объекта? Механизм для этого прост - мы должны найти участок кадра $I_{patch}\in\mathbb{R}^{d=wh}$ , который лучше всего проецируется на базис . Что значит “лучше всего”?

Если рассматривать собственный базис через вероятностный подход, то мы можем определить вероятность того, что объект принадлежит данному базису. Эта вероятность обратно пропорциональна расстоянию от спроецированного объекта до центра базиса $\vec \mu$ . В следующих разделах будет показано, что все чуть сложнее, но для текущего пояснения этого будет достаточно. Очевидно, что объекты, принадлежащие базису будут располагаться близко к центру, в то время как иные объекты будут находиться далеко. Представьте, что на рисунке 1 мы пытаемся спроецировать точку на главную ось $\vec u_1$ . Понятно, что проекция будет находиться далеко от центра , значит маловероятно, что точка принадлежит базису. Теперь предположим, что мы хотим найти участок кадра, в котором находится объект. Для этого я должен найти участок кадра, который лучше всего проецируется на базис объекта $U\in\mathbb{R}^{k\times k}$ ; иными словами, расстояние от которого до базиса $U\in\mathbb{R}^{k\times k}$ минимально.

Чтобы лучше понять, как это будет выглядеть, попробуем представить проекцию на базис в качестве корреляционной функции $f(I_{patch}|U)$ , принимающую на вход участок изображения, окно, фиксированного размера и возвращающую степень принадлежности этого участка базису . Теперь заставим функцию пробежать все изображение, сдвигая наше окно по горизонтали и вертикали. Тогда результатом работы будет новое изображение, в каждой точке которого будет записано расстояние от участка с центром в до базиса.

Рис. 4. Слева оригинальный кадр. Справа результат прогона корреляционной функции по оригинальному кадру. Для удобства визуализации кадр нормирован от 0 до 255, где 255 - наиболее близкое к базису окно. Базис главных компонент обучен на изображениях манекена, стоящего в центре, поэтому корреляционная функция ожидаемо выдала наибольшее значение точке, в которой этот манекен находится.

Задача трекинга в общем виде сложна и подвержена многим ошибкам связанных как с факторами окружения, так и с поведением самого объекта. К первым относятся изменение освещения, движение камеры и всевозможные перекрытия цели другими объектами. Ко вторым относятся изменение позиции и очертания объекта. Для того, чтобы устранить влияние этих факторов или минимизировать их последствия наше признаковое описание (базис главных компонент) не должно быть постоянным, а должно уметь адаптироваться к изменениям. И IVT трекер умеет это делать.

Видео 2. Левое видео: потеря трека на 275 кадре из-за константного базиса. Правое видео: успешное отслеживание авто до конца с помощью инкрементного обучения базиса.

Трюк с адаптацией базиса является ключевой особенностью трекера, что, в свое время, позволило ему выделиться среди других трекеров. Основной вклад авторов данного трекера состоит в том, что они разработали эффективную процедуру обновления базиса главных компонент по мере накопления изменений в кадре. Эту процедуру они назвали Incremental PCA. Таким образом, вместо однократного обучения базиса в начале трекинга мы способны периодически обновлять этот базис по мере движения.

Инкрементное обучение - эффективное обновление базиса главных компонент

Здесь и в дальнейшем будут использованы только основные математические выкладки, необходимые для понимания происходящего. Все, кто интересуются теорией и доказательствами, могут ознакомиться с ними в оригинальной статье [1].

Задача обновления базиса описывается следующим образом. Дана матрица собственных векторов и диагональная матрица собственных значений $\Sigma$ , обученных на первичных изображениях объекта $\mathrm \,\{I_1,...,I_n\}$ . Требуется обучить новый набор $U^{'}$ и $\Sigma^{'}$ на первичных изображениях объекта плюс новых входных изображениях $\mathrm \,\{I_1,...,I_n,I_n+1,...,I_{n+m}\}$ .

Тривиальное решение с переобучением базиса при каждом поступлении новых данных или даже при при поступлении новых данных выглядит неразумно, так как с увеличением количества данных растет размер выделяемой для них оперативной памяти и время вычисления.

Предлагаемый авторами метод инкрементного обучения/обновления собственного базиса, основанный на последовательном Методе Карунена-Лоэва (Sequential Karhunen-Loeve) [4], умеет обновлять базис используя только последние наблюдений, не уничтожая влияние предыдущих наблюдений, следовательно время вычисления всегда постоянно. Сложность данного решения составляет , где - размерность входа, в то время как сложность тривиального решения составляет . Кроме этого, авторы вводят в уравнения обновления коэффициент затухания (forgetting factor), снижающий влияние более старых данных на новый базис, уделяя больше внимания более новым данным. Полное описание алгоритма с формулами для вычисления приведено в статье. На видео 2 представлен пример обновления среднего и собственного базиса.

Итак, мы поняли, что целевой объект будет представляться через базис главных компонент и что это базис будет периодически обновляться для того, чтобы адаптироваться к изменениям. Перейдем теперь к формальной постановки задачи.

Формальная постановка задачи трекинга

Мы будем рассматривать задачу трекинга в рамках стохастического марковского процесса, лежащего в основе движения объекта. Будем считать, что мы владеем априорным знанием того, где находится объект в начальном кадре. Это априорное знание можно получить с помощью нейросетевого детектора. В процессе движения мы наблюдаем данные из которых мы можем вывести апостериорное знание о новом местоположении объекта.

Положение объекта в момент времени будет рассматриваться как скрытое состояние . Это состояние может быть задано многими способами в зависимости от фигуры объекта. Для сохранения общности будем предполагать, что объект заключен в четырехугольную рамку. Тогда состояние представляет собой аффинное преобразование $(x_t,y_t,\theta_t,s_t,\alpha_t,\phi_t)$ для четырехугольника, где параметры в скобках означают координаты центра рамки, угол поворота, масштаб, соотношение сторон и наклон соответственно.

Наблюдаемой величиной будет являться изображение объекта с камеры.

Графическая модель марковского процесса проиллюстрирована ниже.

Рис. 5. Графическое представление скрытой марковской модели.

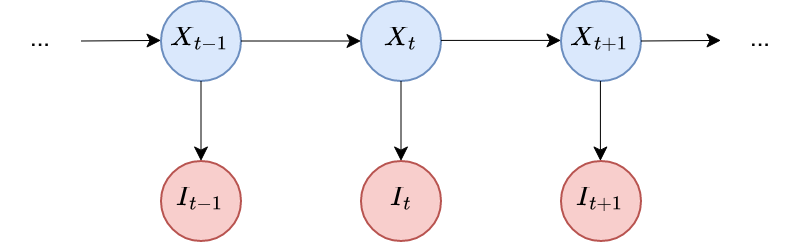
Итак, нам дано начальное положение объекта . Мы получили наблюдение . Требуется предсказать новое местоположение объекта в момент времени . На языке теории вероятностей это выражается как $P(X_1|I_1,X_{0})$ - вероятность при условии и . Применяя теорему Байеса находим

$P(X_1|I_1,X_{0})=\frac{1}{P(I_1|X_{0})}P(X_1|X_{0})P(I_1|X_1,X_{0})$

Опуская лишние зависимости (пользуясь марковским свойством) и отсекая нормировочный коэффициент получаем

$P(X_1|I_1)\propto P(X_1|X_{0})P(I_1|X_1)$

что искомая вероятность пропорциональна произведению двух множителей. Первый множитель это модель движения или “где будет находиться объект в момент времени , при условии, что в момент времени объект находился в $X_{0}$ . Второй множитель это модель наблюдения или “насколько правдоподобно было бы наблюдение , если бы в момент времени объект находился в . В следующих разделах мы рассмотрим эти множители подробнее.

Теперь мы обладаем знанием о местоположении объекта в момент времени . Сделаем один шаг вперед к и пронаблюдаем . Как теперь нам найти местоположение объекта на новом шаге? На самом деле все очевидно. Вспоминаем, что для определения текущего положения нам достаточно знать предыдущее положение объекта и текущее наблюдение. Но мы уже знаем предыдущее местоположение объекта, мы вывели его на шаге , поэтому все, что нужно сделать, это подставить его в формулу в качестве предыдущего наблюдения, то есть $P(X_2|I_2)\propto P(X_2|X_1)P(I_2|X_2)$ .

Все готово к тому, чтобы записать общую рекурсивную формулу для произвольного шага

$P(X_t|I_t)\propto P(X_t|X_{t-1})P(I_t|X_t)$

Можно заметить, насколько элегантно в краткой формуле записывается решение нашей задачи. По сути, в выражении $X_{t-1}$ содержатся (хоть и в проинтегрированном виде) все предыдущие знания о перемещении объекта (оно соответствует верхней горизонтальной стрелочке в графической модели на рисунке 5). На самом деле байесовский вывод возникает естественным образом для моделей последовательной обработки данных, каковой является и наша марковская модель, из-за способности обновлять апостериорное знание по мере поступления новой информации.

Модель движения (dynamical model)

Источник http://www.anuncommonlab.com/articles/how-kalman-filters-work/.

Модель движения задает закон, которому подчиняется движение объекта, то есть переход $P(X_t|X_{t-1})$ от состояния $X_{t-1}$ к состоянию . Он определяется заранее на основе неких теоретических сведений об объекте. Это может быть, например, линейная модель или дифференциальное уравнение произвольного порядка. Так как в этой статье мы рассматриваем отслеживание произвольного объекта, динамика которого нам неизвестна, то в качестве модели движения мы возьмем случайное перемещение объекта в любом из направлений - Броуновское движение. Мы можем записать это движение в виде многомерного нормального распределения ${\mathcal {N}}(X_t|X_{t-1},\Psi)$ , где $\Psi$ - диагональная ковариационная матрица, каждый элемент которой на главной диагонали равен дисперсии одного из параметров, то есть $\Psi={\displaystyle \mathrm {diag} \,\{\sigma^2_x,\sigma^2_y,\sigma^2_\theta,\sigma^2_s,\sigma^2_\alpha,\sigma^2_\phi\}}$ . Иными словами, каждый параметр распределен нормально вокруг своего центра $X_{t-1,p}$ (предыдущего параметра) со среднеквадратичным отклонением $\sigma_p$ .

Геометрически, переход от предыдущего состояния в следующий будет образовывать облако четырехугольников вокруг предыдущего состояния. Новое местоположение объекта, согласно нашей модели, должно оказаться в одном из четырехугольников. В каком именно - решит модель наблюдения.

Рис. 6. Разброс состояний вокруг предыдущего состояния (красный прямоугольник). Каждый синий четырехугольник это гипотеза о местонахождении объекта.

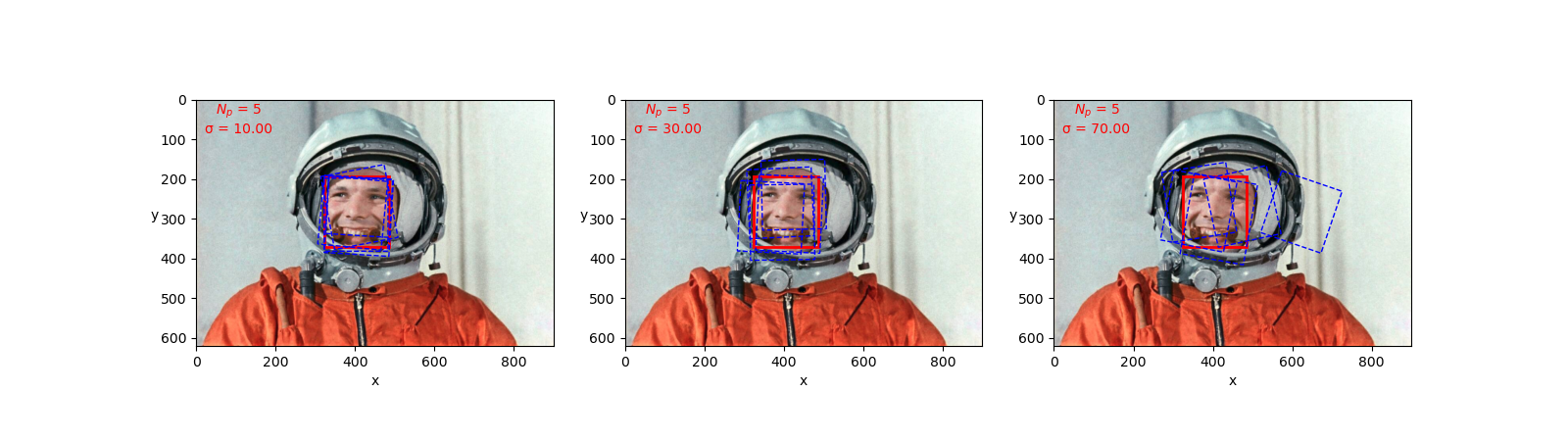
Модель наблюдения (observation model)

Каждое новое наблюдение вносит некую информацию, на основе которой мы можем делать вывод о местонахождении объекта. Для того, чтобы включить эту информацию в модель мы должны задать связь между наблюдением и состоянием . Это и есть модель наблюдения. В байесовской интерпретации модель наблюдения задается распределением - правдоподобием того, что находясь в позиции , мы пронаблюдаем . Так как для наблюдаемого объекта мы моделируем базис с центром $\vec \mu$ , то мы предполагаем, что наблюдение получено из этого базиса. В этом случае распределение имеет следующий смысл: насколько вероятно получить из пространства нашего объекта. Эта вероятность обратно пропорциональна расстоянию от наблюдения до центра $\vec \mu$ . Это расстояние можно разложить на два: расстояние от наблюдения до пространства и расстояние внутри самого пространства от спроецированного до центра. Но для наших целей достаточно будет посчитать только расстояние, пропорциональное :

$P_{d_t}(I_t|X_t)\propto e^{-||(I_t-{\vec \mu})-UU^T(I_t-{\vec \mu})||^2}$

В этом выражении $(I_t-{\vec \mu})$ есть просто исходное изображение объекта за вычетом среднего. Слагаемое $UU^T(I_t-{\vec \mu})$ есть реконструкция исходного изображения, то есть проекция изображения на базис и обратно. Визуально посмотреть на что похожа реконструкция можно на рисунке 4 в рамке под названием recon. Видно, что исходное изображение несколько искажено, из-за потери некоторой составляющей при проецировании, но основной образ сохранен. Тогда разность $(I_t-{\vec \mu})-UU^T(I_t-{\vec \mu})$ , называемая также вектором невязки, есть просто разница между исходным изображением и его реконструкцией, а -норма вектора невязки выражает количество информации, которую мы не можем восстановить. Ясно, что чем больше расстояние , тем ниже вероятность $P_{d_t}(I_t|X_t)$ и тем хуже будет качество восстановленного изображения.

Наглядно расстояния и изображены на рисунке ниже.

Рис. 7. Расстояния до базиса и внутри базиса.

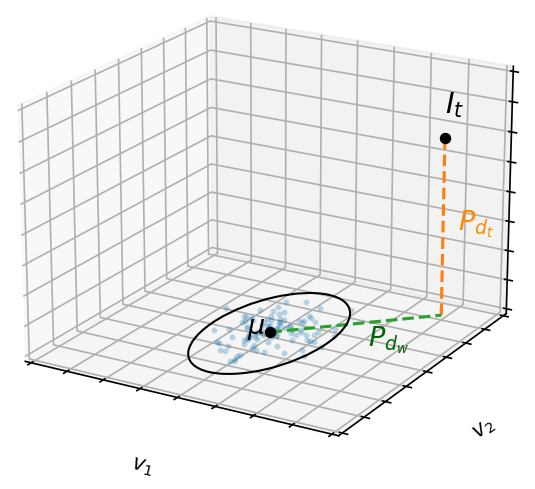
Рис. 7. Расстояние, пропорциональное . Для наглядности базис главных компонент $U\in\mathbb{R}^{2\times 2}$ представлен на плоскости. Мысленно расширяем базис до $U\in\mathbb{R}^{d=wh}$ .

Полезной находкой авторов оказалось использование робастной функции $\rho(x,\sigma)={x^2}/({\sigma^2+x^2)}$ вместо -нормы для минимизации влияния шумовых пикселей на оценку вероятности $P_{d_t}(I_t|X_t)$ . Действительно, если целевой объект имеет круглую форму и, при этом, заключен в прямоугольную рамку, то краевые пиксели внутри рамки, выходящие за периметр круга, будут явно помехой. Смысл параметра $\sigma$ в том, что он задает критическую область, после которой влияние шумов на модель наблюдения начинает уменьшаться [2].

Сэмплирование - как вычислить произвольное распределение

Единственное, на чем мы пока не заостряли внимания, это на том, какую форму должно иметь распределение . Поначалу это распределение приближали обычным гауссианом предполагая, что существует только одна наиболее вероятная точка, в которой должен находиться объект. Предсказание местоположения таким образом сводилось к оценке параметров движения фильтром Калмана. Однако, несмотря на то, что это удобное средство моделирования, на практике оно не всегда адекватно описывает процесс. Из-за наличия сложного фона и непредсказуемой динамики движения объекта было бы правильнее выдвигать сразу несколько гипотез о том, где может находиться объект и принимать наиболее вероятную из них. Поэтому мы будем считать, что распределение имеет несколько вершин.

Рис. 8. Апостериорное распространение для x-координаты по дискретным отсчетам t. Видно, что в начале модель уверена в положении объекта (лицо человека в красной рамке), но по мере движения начинают образовываться несколько гипотез. Например, на отметке t=20 на левом графике видно три вершины. Самая левая вершина соответствует цели, вершина посередине соответствует похожему человеку справа от цели и правая вершина соответствует человеку в синей жилетке справа. Так как человек справа находится далеко от цели, то модель справедливо дает ему наименьший вес полагая, что цель не сможет так резко сдвинуться вправо.

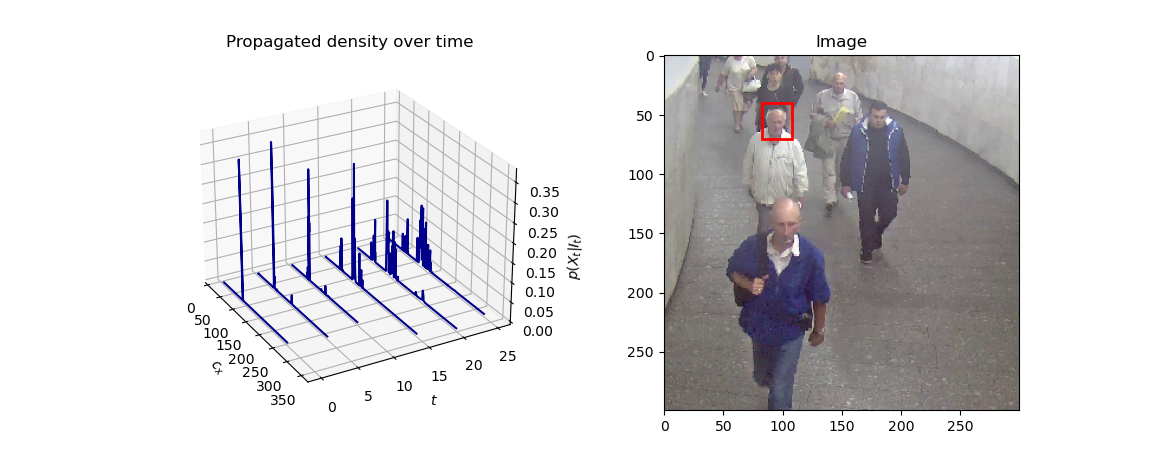
Поскольку теперь распределение имеет произвольную форму, отличную от гауссиана, мы теряем возможность вычислить его аналитически. Поэтому мы применим технику фильтра частиц (particle filter), позволяющую оценить параметры искомого произвольного распределения. Можно считать, что это обобщение фильтра Калмана на случай негауссовских процессов. Под частицей понимается элемент $\hat x^{(i)}$ из выборочной совокупности ${\hat {X_t}}$ распределения с весом, пропорциональным вероятности получить эту частицу из распределения. На рисунке 8 частицей является каждая темно-синяя точка на левом графике. Если устремить количество частиц в бесконечность, то “рваный” график будет становиться более гладким, а в пределе станет непрерывным. Заметно, что частица с наибольшим весом соответствует наиболее вероятному местоположению объекта. Для генерации и распространения частиц во времени мы воспользуемся алгоритмом сэмплирования CONDENSATION [3].

Алгоритм CONDENSATION использует технику сэмплирования с учетом динамики движения объекта для генерации выборки из частиц подчиняемых распределению . Данный алгоритм итеративный. Это значит, что получив выборку из апостериорного распределения мы можем распространить эту выборку для вычисления нового апостериорного распределения на следующем шаге $P(X_{t+1}|I_{t+1})$ используя предыдущее распределение в качестве априорного. Этап распространения при этом переживают только частицы с наибольшим весом, в то время как маловероятные частицы отсеиваются. Вычислительная сложность алгоритма оценивается как .

Упрощенно, схему CONDENSATION можно представить в следующем виде:

Генерируем случайную выборку ${\hat {X_t}}$ из распределения $P(X_t|X_{t-1}={\hat {X}_{t-1}})$ .
Каждому элементу выборки присваиваем вес $\pi_t$ , равный $P(I_t|X_t={\hat {X_t}})$ .
Нормализуем выборку ${\hat {X_t}}$ для удовлетворения условия $\sum_{n\mathop {=} 1}^{N_p}\pi^{(n)}_t=1$ .
Вычисляем необходимые статистики, например
- мат. ожидание $E[X_t|I_t]\approx \sum_{n=1}^{N_p} {\pi^{(n)}_t {\hat{X}_t^{(n)}}}$
- моменты $E[f(X_t)|I_t]\approx \sum_{n=1}^{N_p} {\pi^{(n)}_t f({\hat{X}_t^{(n)})}}$
- наиболее вероятное состояние объекта $max({\hat {X_t}})$
Нам интересен последний случай. Данные статистики асимптотически несмещенные.
Переходим к следующему такту и повторяем процедуру с первого шага принимая за ${\hat {X}_{t-1}}$ (см. первый шаг) выборку $\hat{X_{t}}$ .

Таким образом, несмотря на то, что мы не в состоянии численно выразить распределение $P(X_t|X_{t-1})$ , мы можем найти необходимые статистики этого распределения через выборочную совокупность ${\hat {X_t}}$ . А для решения нашей задачи этого достаточно.

Соединяем все вместе

Наконец, мы владеем всей необходимой информацией и можем записать полную схему работы трекера:

Используя детектор объектов (нейросетевой или статистический, не имеет значения) определяем местоположение объекта на начальном кадре . Задаем всем частицам значение начальной позиции объекта с равным весом .
Задаем пустой базис со средним значением $\vec \mu$ равным изображению объекта на начальном кадре.
Двигаемся к следующему кадру . Генерируем новые частицы/возможные местоположения в соответствии с динамической моделью $P(X_1|X_{0})$ .
Для каждой частицы извлекаем соответствующий кроп $I^{(i)}_{1}$ из текущего кадра и вычисляем ее вес в соответствии с моделью наблюдения $P(I^{(i)}_{1}|X_1=i)$ .
Сохраняем частицу с наибольшим весом. После того, как будет накоплено кадров осуществляем инкрементное обучение базиса и среднего $\vec \mu$ .
Возвращаемся к шагу 3.

Особенности реализации и эксперименты

Для тестирования трекера была разработана демка на C++, в основе которой лежит код Matlab от авторов оригинальной статьи.

В реальных задачах мы сталкиваемся с физическими ограничениями. Во-первых, мы ограничены железом, ввиду чего мы не можем аппроксимировать распределение с любой точностью и вынуждены ограничивать количество генерируемых частиц . Еще одно ограничение связано с тем, что при переходе $P(X_t|X_{t-1})$ координаты некоторых частиц могут “вылететь” за рамки кадра. Мы не будем утруждать себя отдельной обработкой таких случаев, а будем просто возводить такие частицы в нулевой вектор, что эквивалентно обнулению веса частицы.

Для сокращения времени вычислений мы не будем использовать параметры поворота и сдвига для состояния и оставим только четыре параметра $(x_t,y_t,s_t,\alpha_t)$ : координаты центра, масштаб и соотношение сторон; с их помощью можно задать любой неповоротный прямоугольник.

Имея в качестве начальной конфигурации трекера размер окна 32 на 32 мы получаем от 125 до 8 кадров в секунду на стареньком Intel Core i7 4700HQ 2.4 Мгц при количестве частиц от 100 до 1000 соответственно. Другие параметры не сильно сказываются на производительности. Подробный тренд представлен на рисунках ниже.

Рис. 9. Показания среднего времени вычисления.

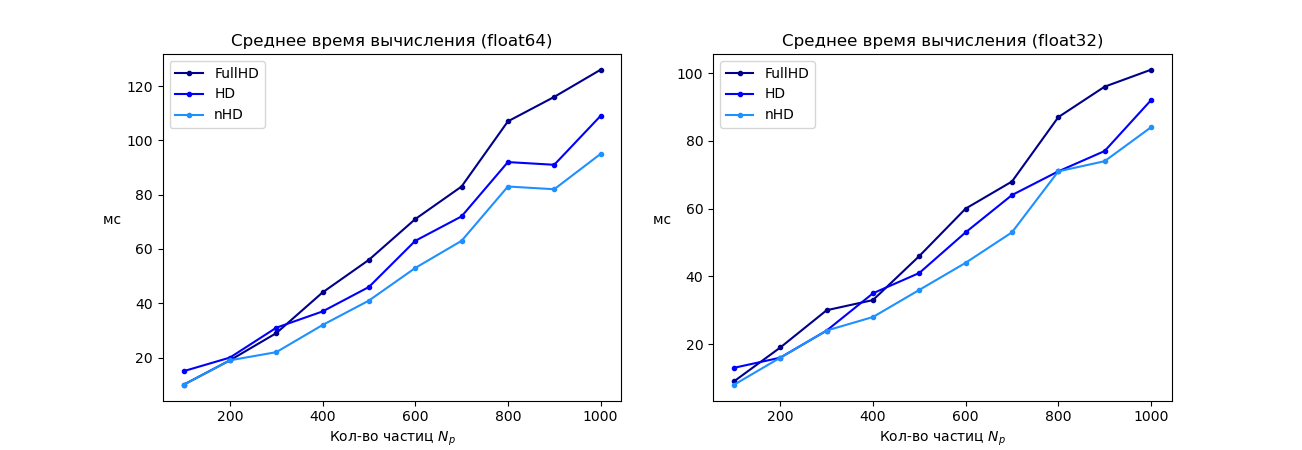
На видео ниже приведены некоторые примеры работы трекера на сценах различной сложности, как удачные так и неудачные.

Стоит отметить, что, конечно, векторы коэффициентов в базисе главных компонент не являются настолько выразительными признаками как признаки аппроксимированные глубокой нейросетью. При тестировании трекера это дает о себе знать. Например, нередко возникает ситуация когда состояние может “перескочить” на другой объект, посчитав его за целевой (см. отслеживание северного оленя на видео выше). Другая проблема связана с тем, что объекты с примитивной текстурой, без ярко выраженных визуальных признаков, плохо моделируются базисом. Следствием этого является то, что модель наблюдения не может дать особого предпочтения для какой-то из гипотез и состояние не может зацепиться за конкретный объект, а начинает случайно блуждать по сцене (см. отслеживание Усейна Болта на видео выше).

Так же, что характерно для всех аналогичных трекеров того времени, для работы в конкретных условиях его нужно настраивать. Но по опыту можно сказать, что настройки по умолчанию (их можно подсмотреть в репозитории) покрывают бóльшую часть сценариев и всю настройку можно свести к подгонке модели движения.

Подводя практический итог можно сказать, что трекер хорошо справляется с отслеживанием объектов сложной текстуры на краткосрочных и среднесрочных треках, таких как лица, транспортные средства. При наблюдении за объектом на длинных временных дистанциях велик риск упустить истинное положение объекта и начать отслеживать не то, что нужно. При частичном перекрытии объекта трекер способен удерживать позицию, но при сильном перекрытии теряет объект из виду.

Несомненным преимуществом трекера является то, что нам не обязательно иметь предобученный базис, как этого требует, например, DeepSORT, хотя никто не запрещает предварительно обучить базис на целевом объекте и использовать его в качестве начального, вместо пустого (см. шаг 2 общего алгоритма).

Заключение

Несмотря на то, что этот трекер уже не современный и с появлением нейросетевых моделей постепенно отходит на второй план, это все же интересный пример использования метода главных компонент, который полезно рассмотреть как минимум в образовательных целях и как максимум применить его в тех случаях, когда нейросетевая обработка слишком дорога или когда требуется высокая частота обработки кадров. Идею же инкрементного обучения можно подхватить при реализации других CV-алгоритмов.

Надеюсь материал оказался не слишком нагруженным и каждый нашел в нем для себя что-то полезное.

Ссылки

D. Ross, J. Lim, R. S. Lin, M. H. Yang. Incremental Learning for Robust Visual Tracking. 2008.
M. J. Black and A. D. Jepson. Eigentracking: Robust matching and tracking of articulated objects using view-based representation. 1996.
M. Isard and A. Blake. Contour tracking by stochastic propagation of conditional density. 1996.
A. Levy and M. Lindenbaum. Sequential Karhunen-Loeve basis extraction and its application to images. 2000.