Обычно, когда мы говорим о беспилотных летательных аппаратах (БПЛА) [1], на ум сразу приходит квадрокоптер (или другой представитель класса мультикоптеров, например, гекса- или октокоптер). Но строго говоря, беспилотник не обязательно должен быть мультикоптером – он может быть выполнен в виде любой механической схемы, которая ранее была разработана для пилотируемого полёта.
Например, это может быть летательный аппарат легче воздуха, то есть аэростат (воздушный шар) или дирижабль [2]. Данной статьёй мы открываем цикл публикаций, в котором расскажем в режиме «хроник лаборатории» о ходе нашего сайд-проекта по сборке БПЛА в виде стратостата [3]. Но прежде, чем что-то собирать, нужно хорошо разобраться в предмете, в его теоретической части. Поэтому мы решили начать с того, чтобы изучить динамику вертикального полёта воздушного шара.

Ничего принципиально нового, что бы не было известно до нас, мы на этом пути, конечно же, не открыли, но такой цели перед нами и не стояло. Сайд-проект, в первую очередь, делается ради интереса, для того, чтобы разработать и сконструировать что-то самим, а не только читать о чужих достижениях. В настоящей статье мы постарались изложить доступным языком основы динамики вертикального полёта аэростата, учитывая те сложности и ошибки, с которыми столкнулись сами при изучении материала.
1. Какие силы действуют на воздушный шар
Динамика полёта воздушного шара – вещь непростая и довольно капризная, так как приходится учитывать поведение ветра, которое не очень-то предсказуемо по своей природе. Именно поэтому, чтобы не утонуть на первых же шагах в чрезмерных сложностях, мы решили упростить задачу и ограничиться рассмотрением только вертикального полёта, то есть взлёта, набора высоты, снижения и посадки.
Для начала давайте разберёмся, какие силы действуют на аэростат и почему он вообще летает (а в более общей постановке вопроса – почему он изменяет свою высоту, то поднимаясь вверх, то опускаясь вниз).

Вертикальный полёт аэростата определяется тремя силами: силой тяжести, архимедовой силой и силой сопротивления воздуха.
1.1. Сила тяжести
Обозначим за«сухую» массу аэростата (гондола, пустая оболочка, стропы), а за
– массу газа в оболочке, которая, в свою очередь, зависит от плотности газа в оболочке
и её объёма
как
. Отсюда полная масса аэростата
Сила тяжести, действующая на аэростат,
и направлена всегда вниз.
1.2. Архимедова сила
Архимедова сила
направлена всегда вверх, и именно она заставляет аэростат подниматься. Поэтому эту силу ещё называют подъёмной.здесь – плотность внешнего воздуха (атмосферы, в которой летит наш воздушный шар), а
, как мы уже говорили выше, – объём оболочки, наполненной газом легче воздуха. Строго говоря, для архимедовой силы в качестве объёма
нужно брать объём всего аэростата, включая и гондолу. Но поскольку её объём существенно меньше объёма оболочки, будем для упрощения расчётов рассматривать только объём «собственно шара».
На самом деле (как видно, например, на фотографии), оболочка аэростата не является строго сферической, и иногда отклонение её формы от сферы может быть значительным. Однако мы примем допущение о сферичности оболочки для упрощения расчётов, и вот почему:
во многих случаях форма оболочки не сильно отличается от сферической;
допущение о сферичности оболочки значительно упрощает расчёты, связанные с силой лобового сопротивления и присоединённой массой (см. ниже). В противном случае, если мы решим не делать никаких допущений, касающихся геометрии аэростата, нам придётся прибегнуть к полноценному арсеналу CFD, что слишком далеко выходит за рамки нашей задачи.
Итак, пусть оболочка аэростата представляет собой шар радиусом. Тогда объём оболочки
. В дальнейшем нам понадобится также площадь поперечного сечения шара (круга радиусом
)
. Используя это выражение мы можем записать
, откуда архимедова сила
1.3. Сила сопротивления воздуха
Сила сопротивления воздуха
направлена против движения аэростата, то есть вниз при взлёте и наборе высоты, и вверх при снижении и посадке.
здесь – характерная площадь лобового сопротивления, в нашем случае площадь поперечного сечения шара (круга радиусом
), которую мы уже рассмотрели выше. (Обратите ещё раз внимание:
– площадь поперечного сечения шара, а не его поверхности).
– безразмерный коэффициент сопротивления формы, который для шара равен
[W1].
– по-прежнему плотность внешнего воздуха (атмосферы), то есть среды, в которой осуществляется полёт и которая оказывает сопротивление.
– вертикальная скорость шара [4].
1.4. Присоединённая масса
Отсюда второй закон Ньютона для шара в векторном виде будет выглядеть следующим образом:
где– ускорение воздушного шара,
– его масса (см. (1)), а
– присоединённая масса. Что это такое?
Дело в том, что когда объект двигается ускоренно в среде (жидкости или газе), он должен сообщить своё ускорение некоторому объёму этой среды, чтобы перед объектом не образовывалось уплотнений, а за объектом разряжений [С1]. Выглядит это так, как будто бы к объекту «присоединяется» дополнительная масса, двигающаяся вместе с ним и равная
где коэффициентзависит от формы объекта и направления движения относительно его осей инерции. Для сферы
, и тогда мы можем записать, что
2. Как рассчитать ускорение воздушного шара
Прежде, чем переходить к алгебраической записи второго закона Ньютона для аэростата, договоримся, что положительное направление осибудет направлено вверх. Таким образом, скорость
шара положительна, если он набирает высоту (летит вверх), и отрицательна, если он снижается (летит вниз). Ускорение свободного падения
соответственно, будет отрицательным; ускорение, вызванное архимедовой силой – положительным; а ускорение, вызванное силой сопротивления воздуха, будет иметь знак, противоположный знаку скорости
.
Теперь запишем компоненты уравнения (6) в алгебраическом виде:
(так как сила тяжести всегда направлена вниз)
Знакздесь показывает, что сила сопротивления воздуха
направлена вниз при подъёме шара и вверх при его спуске.
Правомерно также задать следующий вопрос: а стоит ли вообще учитывать силу сопротивления воздуха? Насколько значительный вклад она вносит в суммарное ускорение аэростата? Забегая вперёд, скажем, что да – стоит. Результаты численного моделирования, которые мы приведём в следующей статье, демонстрируют, что ускорение, создаваемое силой сопротивление воздуха, по порядку составляетот общего ускорения воздушного шара.
Выпишем теперь полное уравнение:
разделим его наи получим
Теперь немного «поколдуем» с формулой (12), чтобы сделать её проще и удобнее для вычислений. Во-первых, обратим внимание на то, что в числителе у нас есть общий множитель у обоих слагаемых – плотность. Во-вторых, так как
,
. Учитывая вышесказанное, имеем
В некоторых источниках встречается понятие приведённой плотности
которая показывает, какая бы плотность была у аэростата, если бы вся его масса (гондола, оболочка, газ в оболочке) и присоединённая масса были размещены внутри самой оболочки. Используя приведённую плотность, формулу (14) можно переписать в виде
Итак, мы получили уравнение, ради которого все вышеприведённые математические выкладки и затевались. Оно описывает зависимость ускорения аэростата от других кинематических характеристик (скорости), параметров конструкции аэростата (массы и объёма, «замаскированных» под приведённую плотность и радиус оболочки) и параметров внешней среды (плотности воздуха и ускорения свободного падения).
Такие величины, как ускорение свободного падения, плотность воздуха
, объём оболочки аэростата
и его скорость
не являются постоянными.
и
убывают по мере набора высоты. Уменьшение плотности воздуха в высоких слоях атмосферы приводит к уменьшению его давления, что, как следствие, приводит к увеличению объёма оболочки аэростата. Наконец, скорость аэростата изменяется всегда, когда ускорение
. Таким образом, уравнение (16) описывает именно мгновенное ускорение аэростата в данный момент времени.
В следующей статье мы расскажем о том, как решать это уравнение, чтобы получить значения высоты полёта, скорости и ускорения аэростата для заданных моментов времени, учитывая «непостоянство» плотности внешнего воздуха и других величин.
UPD. В статью добавлен учёт присоединённой массы, а также сакцентировано внимание на том, что уравнения (14) и (16) описывают мгновенное ускорение. Авторы благодарят @encyclopedistи @sshikovза полезные комментарии.
Примечания
[1] Далее термины «беспилотный летательный аппарат», «беспилотник», «дрон» и сокращение БПЛА мы будем употреблять как синонимы.
[2] Основное отличие аэростата от дирижабля с точки зрения механики состоит в том, что дирижабль оснащён силовой установкой и может управляемо перемещаться в заданном направлении в горизонтальной плоскости, в то время как перемещения аэростата в горизонтальной плоскости носят неуправляемый характер, он летит туда, куда дует ветер.
[3] Хотя в конечном счёте проект будет посвящён сборке стратостата, начнём мы с обычного аэростата. Основное отличие между ними состоит в том, что аэростат предназначен для полётов в тропосфере (то есть на высотах до 11 км), а стратостат – в более высоких слоях атмосферы. Очень низкое атмосферное давление в высоких слоях накладывает на стратостаты дополнительные требования по прочности конструкции. Но уравнения динамики вертикального полёта аэростата и стратостата одинаковы, поэтому дальше, в целях упрощения изложения, мы везде будем использовать термин «аэростат» как более общий (стратостаты являются подклассом аэростатов) или же синонимичный ему термин «воздушный шар».
[4] В дальнейшем, когда мы будем говорить о скорости аэростата и его ускорении, мы будем иметь ввиду именно вертикальные скорость и ускорение.
Ссылки
[W1] Коэффициент сопротивления формы – https://ru.wikipedia.org/wiki/Коэффициент_сопротивления_формы
[С1] Стасенко А. Л. Физические основы полёта. – М.: Бюро Квантум, 2005. – 256 с. (Библиотечка «Квант». Вып. 91. Приложение к журналу «Квант» №6/2005).
Комментарии (25)

sshikov
04.11.2022 21:19+1Если вы не учитываете изменение плотности воздуха/газа внутри (да пожалуй что и снаружи) при нагреве/охлаждении (что непосредственно влияет на архимедову силу), то и аэродинамическим сопротивлением вполне можно пренебречь. Это будет того же уровня допущение.
Скажем, самые простые шары, которые в моем детстве делались из бумаги, летали только за счет того, что заполнялись теплым воздухом. И как только он остывал, начинали опускаться. Если этим и можно пренебречь (для гелия, например), то такие допущения нужно озвучивать.
При этом типичная скорость полета как правило настолько мала (метры в секунду), что думая про аэродинамическое сопротивление, скорее стоило бы учитывать ветер, который бывает и 10 метров в секунду, и больше.
hbn3
04.11.2022 21:29+1который бывает и 10 метров в секунду
На 11 км бывают очень сильные ветра. Недавно например была заметка как пассажирский самолёт летел со скоростью больше скорости звука (относительно земли), как раз за счёт попутного ветра (370км/ч).
sshikov
04.11.2022 21:45>10 метров в секунду, и больше.
Ну да. Просто для моего вывода достаточно того, что вполне бытовая скорость ветра 10 м/сек это уже возможно на порядок выше скорости подъема аэростата. А с учетом того, что в сопротивлении скорость в квадрате — то мы уже два порядка имеем. А если речь про 11 км — то температуру станет просто обязательно учитывать (да там и плотность воздуха вовсе не константа уже). В общем, этой модели не хватает ограничений, в которых она применима.

ShashkovS
05.11.2022 18:29Вот есть карта ветров на высоте 12км: https://www.ventusky.com/?p=1;7;1&l=wind-200hpa
250км/ч там ооочень мнгого где. 370км/ч конечно должно повезти.

tormozedison
07.11.2022 13:57А пассажиры не испугались, увидев на внутрисалонных дисплеях такую скорость?

DmitryKryzhanovskiy Автор
04.11.2022 22:30+1Изменение плотности и давления внешнего воздуха с высотой и давления внутри оболочки мы учитываем. Об этом как раз был комментарий [6] в статье, и значительная часть следующего поста будет о том, как именно мы эти изменения учитываем при вычислениях. Формула же (9) описывает именно мгновенное ускорение. Она нужна, чтобы перейти к дифференциальным уравнениям для вычисления высоты, скорости и ускорения в каждый момент времени.
Ветер на первом этапе мы в расчёт не берём, чтобы не усложнять задачу, но по сути комментария согласен - в будущем добавим его в модель как входное воздействие.
Насчёт скоростей - в одной из статей на Хабре я видел в комментариях обсуждение, стоит ли учитывать сопротивление воздуха для воздушного шара, так как характерная скорость достаточно мала. Расчёты показали, что стоит (детали будут в следующем посту): ускорение свободного падения примерно -9,8 м/с2; ускорение, создаваемое архмедовой силой, по модулю приблизительно такое же, но направлено вверх. Их равнодействующая по модулю имеет значения порядка 1 м/с2 и меньше (вплоть до высоты, где сила тяжести сравняется с архимедовой). Но примерно такого же порядка ускорение, создаваемое лобовым сопротивлением. Так что в итоге его вклад в суммарное ускорение шара оказывается существенным.

sshikov
04.11.2022 22:50Да, вы правы, я как-то этот комментарий пропустил похоже.
>Насчёт скоростей — в одной из статей на Хабре я видел в комментариях обсуждение, стоит ли учитывать сопротивление воздуха для воздушного шара, так как характерная скорость достаточно мала.
Да я помню тут статью, и даже вроде участвовал в обсуждении. Насколько я помню, сошлись примерно на том, что вклад сопротивления хоть и мал, но в основном именно он ограничивает рост скорости подъема.

belch84
04.11.2022 22:49Приблизительная зависимость плотности от высоты — экспоненциальная
,
где Hn = 10.4 км
Формула приведена в статье о плотности воздуха в английской Википедии. Вроде бы, формула учитывает изменение температуры с высотой
sshikov
04.11.2022 22:53Так вроде температура сама нам не особо нужна. Тут и архимедова сила, и сопротивление — они от самой плотности зависят.

belch84
04.11.2022 23:01Так вроде температура сама нам не особо нужна. Тут и архимедова сила, и сопротивление — они от самой плотности зависят.
Температура не нужна, но плотность от температуры зависит. По ссылке указано, почему для этой формулы температурой можно пренебречь
sshikov
04.11.2022 23:15Ну кстати, подозреваю что температура газа внутри баллона вполне может отличаться от температуры снаружи (да и газ в общем случае другой). Если баллон подогревается (что тоже вполне типично), то учитывать надо и это.

Radisto
05.11.2022 12:39Если не ошибаюсь, еще у Пикара он солнцем нагревался, и когда солнце село, пошел на снижение

DmitryKryzhanovskiy Автор
05.11.2022 19:45Я читал, что у Пикара за счёт нагрева солнечными лучами планировалось осуществлять терморегуляцию гондолы (что не очень сработало, температура в «салоне» поднялась до +38 °C). Насчёт нагрева и остывания оболочки за счёт солнечного излучения / его отсутствия – здесь прокомментировать не могу. Такой информации мне не попадалось, но и опровержения её я тоже не видел )

DmitryKryzhanovskiy Автор
05.11.2022 19:38Там с температурой, давлением и плотностью всё непросто. Подробно об этом будем рассказывать во второй статье. Если вкратце, то падение давления и плотности атмосферы нужно обязательно учитывать (оно значительное), причём для каждого слоя атмосферы свои коэффициенты, которые описывают эту зависимость.
Газ внутри оболочки, конечно же, отличается от газа снаружи - либо по составу (молярная масса), либо по температуре, либо всё вместе. И один вопрос, который мы пока для себя так и не выяснили - что считать температурой газа в оболочке. Допустим, у нас в гондоле установлена горелка, и мы нагреваем воздух до 100 °C. Но оболочка - вещь немаленькая, это десятки метров в поперечнике. Понятно, что до температуры 100 °C воздух прогреется далеко не сразу. В текущей версии модели мы не углублялись в тонкости теплообмена, происходящего в оболочке, но возможно, всё-таки придётся.

belch84
04.11.2022 23:54+2A
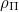 постоянно? Выписал дифференциальное уравнение, придумал подходящие параметры, порешал — получилось, что, достигнув некоторой высоты, аэростат начинает совершать небольшие плавные колебания вверх-вниз
постоянно? Выписал дифференциальное уравнение, придумал подходящие параметры, порешал — получилось, что, достигнув некоторой высоты, аэростат начинает совершать небольшие плавные колебания вверх-вниз
DmitryKryzhanovskiy Автор
05.11.2022 19:17Да, всё верно, после достижения максимальной высоты аэростат будет совершать небольшие колебания по высоте, амплитуда которых будет постепенно затухать. Например, для массы гондолы 200 кг, радиуса оболочки 7 м, газ в оболочке - воздух, нагретый до 100 °C, максимальная высота у нас получилась около 950 м, амплитуда колебаний - сначала ±10 м, к концу первого часа затухает до ±10 см.

DmitryKryzhanovskiy Автор
05.11.2022 19:19Что касается ρП, то, строго говоря, она не постоянно, так как объём оболочки с высотой возрастает. Однако для примерных оценок для тропосферы (высота до 11 км) его можно принять постоянным, но, оговоримся - для примерных оценок.

MishaRash
05.11.2022 22:22Однако для примерных оценок для тропосферы (высота до 11 км) его можно принять постоянным, но, оговоримся - для примерных оценок.
До 11 км должно быть довольно грубо. Характерная высота атмосферы Земли оценивается как 6-8.5 км - при таком изменении плотность падает примерно в
раз.

DmitryKryzhanovskiy Автор
05.11.2022 19:22А такой вопрос для любопытства - вы дифур решали аналитически или численно? Спрашиваю, так как мы сразу же отказались от идеи аналитического решения (в следующей статье расскажу, почему), но интересно, если кто решит аналитически, какие уравнения получатся.

belch84
05.11.2022 20:46А такой вопрос для любопытства — вы дифур решали аналитически или численно?
Численно, конечно, используя вот эту свою собственную программу для численного интегрирования диффуравнений. Кстати, система оказалась жесткой, пришлось применять численный метод для жестких систем. Для плотности воздуха использовал формулу, приведенную в моём комментарии выше. Параметры были такие: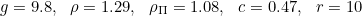
Картинки получились такие:Аэростат, зависимость высоты от времени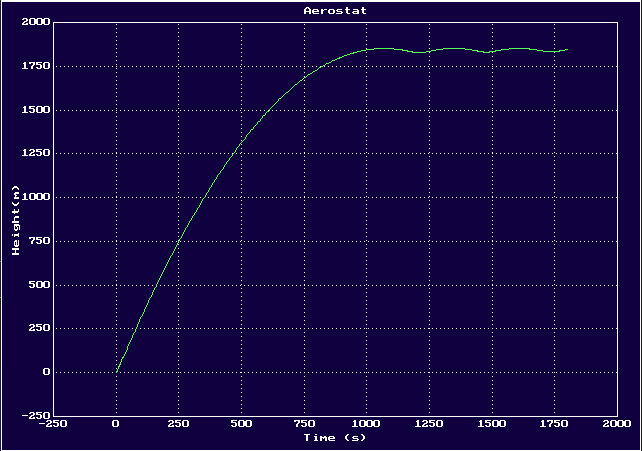

DmitryKryzhanovskiy Автор
06.11.2022 20:06Спасибо большое за комментарий! ????????
Да, у нас характер графиков такой же (подробно покажем в следующей статье).
Спасибо за ссылку на ваш пост – очень полезный материал!


 постоянно? Выписал дифференциальное уравнение, придумал подходящие параметры, порешал — получилось, что, достигнув некоторой высоты, аэростат начинает совершать небольшие плавные колебания вверх-вниз
постоянно? Выписал дифференциальное уравнение, придумал подходящие параметры, порешал — получилось, что, достигнув некоторой высоты, аэростат начинает совершать небольшие плавные колебания вверх-вниз


encyclopedist
Вы забыли присоединенную массу
Также, в силе сопротивления можно записать вместо
вместо  , тогда не нужно будет писать
, тогда не нужно будет писать 
DmitryKryzhanovskiy Автор
Спасибо за комментарий про присоединённую массу. Мы действительно про неё забыли - сейчас будем вносить изменения в модель и в текст статьи.
Про – согласен, это позволит избежать знака ∓, но такую форму мы выбрали, так как с ней потом легче работать при разработке и отладке кода.
– согласен, это позволит избежать знака ∓, но такую форму мы выбрали, так как с ней потом легче работать при разработке и отладке кода.
novoselov
Раз уж в расчетах вся масса аэростата сосредоточена в объеме шара, то интересно было бы посчитать "летающие города" по задумке Бакминстера Фуллера
https://en.wikipedia.org/wiki/Cloud_Nine_(sphere)