Я уже не знаю кому и чему верить. Собрался было подводить итоги по обсуждению аттрактора Лоренца, но что-то меня заставило "поиграть" еще с одним - мотором Рикитаке [1]. И, честное слово, какого-либо подвоха я, ну, никак  не ожидал. Просто потому, что по виду графиков он был, пожалуй, наиболее стабильным и характерным по внешнему виду во всех программных пакетах - MATLAB, SimInTech и ВКПа (cм. также предыдущую статью [2]).

            На структурном уровне рассматриваемые аттракторы можно представить в виде трех блоков ("черных ящиков"), отличающихся лишь видом связей. Структурная модель аттрактора Рикитаке представлена на рис. 1а, а на рис. 1б для сравнения приведена схема аттрактора Лоренца.

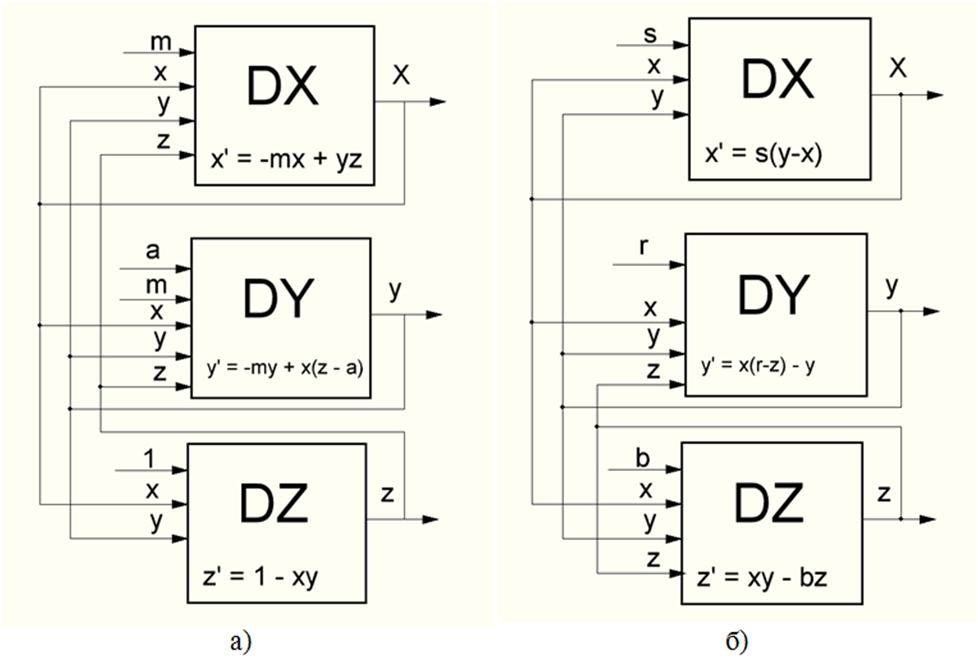
            Напомним, аттрактор Рикитаке описывается следующей системой уравнений (уравнения аттрактора Лоренца см. в [1]):

            Для совсем полного погружения в проблему приведем реализацию блока DX на языке С++ в рамках ВКПа, где он выглядит следующим образом:

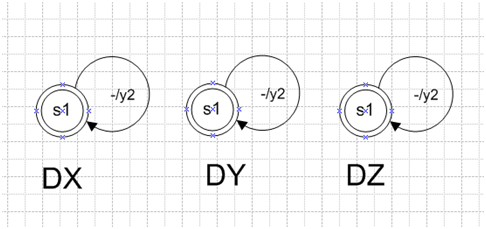
Здесь у2 - действие, выполняемое автоматом на каждом такте дискретного времени. Для остальных блоков - DY и DZ код аналогичен, отличаясь лишь формулой расчета входного сигнала для интегрирующей части. Используемая при этом сетевая автоматная модель решения дифференциальных уравнений 3-го порядка показана на рис. 3.

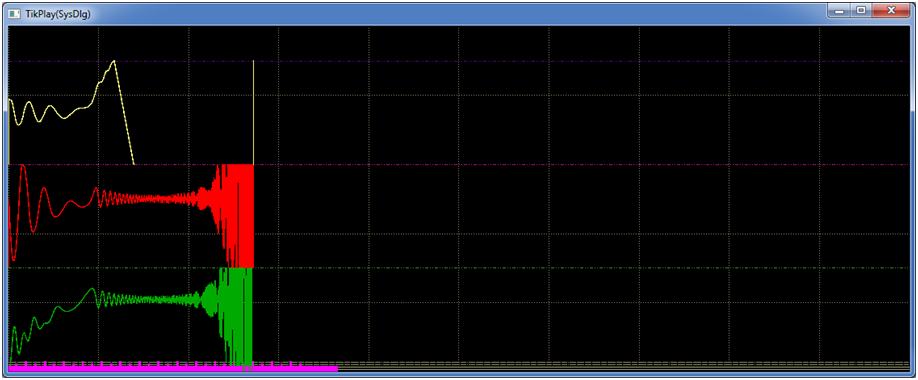
            Вид сигналов для решения, соответствующего  приведенной выше структурной схеме показан на рис. 4. И он настолько неожиданный, что первая реакция - ошибка в коде. Но многократный и внимательный просмотр показал - все верно.

            И тогда было принято решение разбить каждый блок на два. Где первый - входной блок, выполняет расчет входной формулы (см. правую часть уравнений), а второй - собственно интегратор. После подобной "операции" получился результат (а он, заметим, одинаков во всех двух режимах работы ВКПа), приведенный на рис. 5.

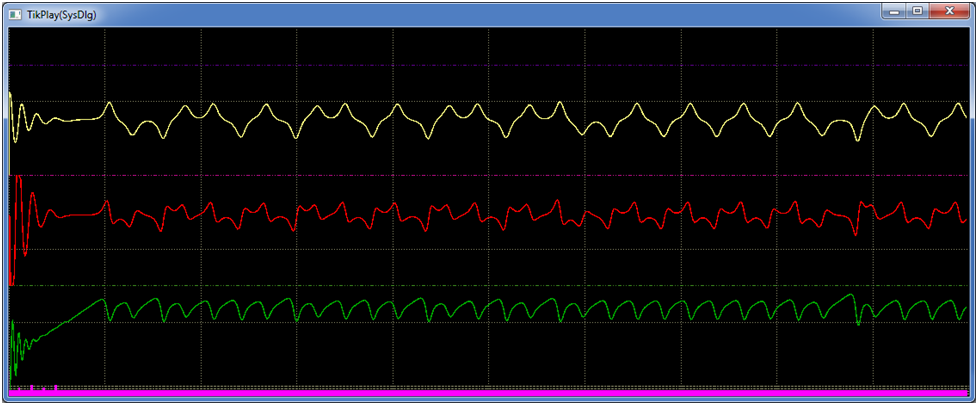
             Ба! Да он походит на ранее полученные решения! А они, чтобы не быть голословными, показаны на рис. 6, 7. Значит, реализация входных блоков не содержит ошибок.

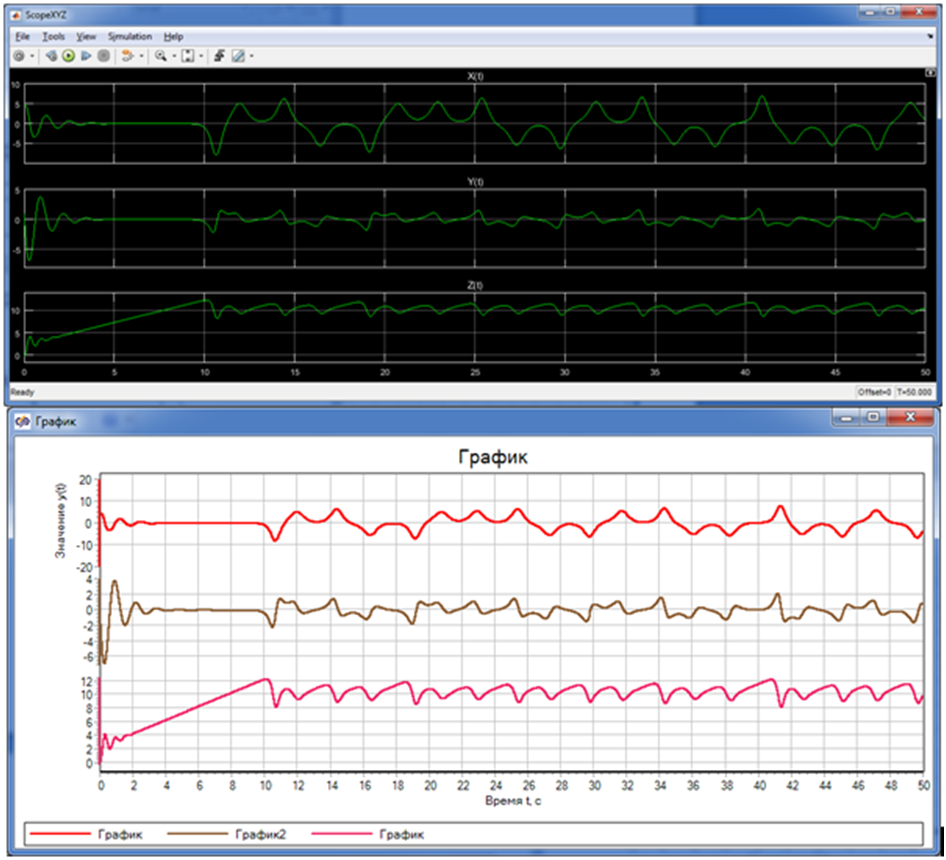
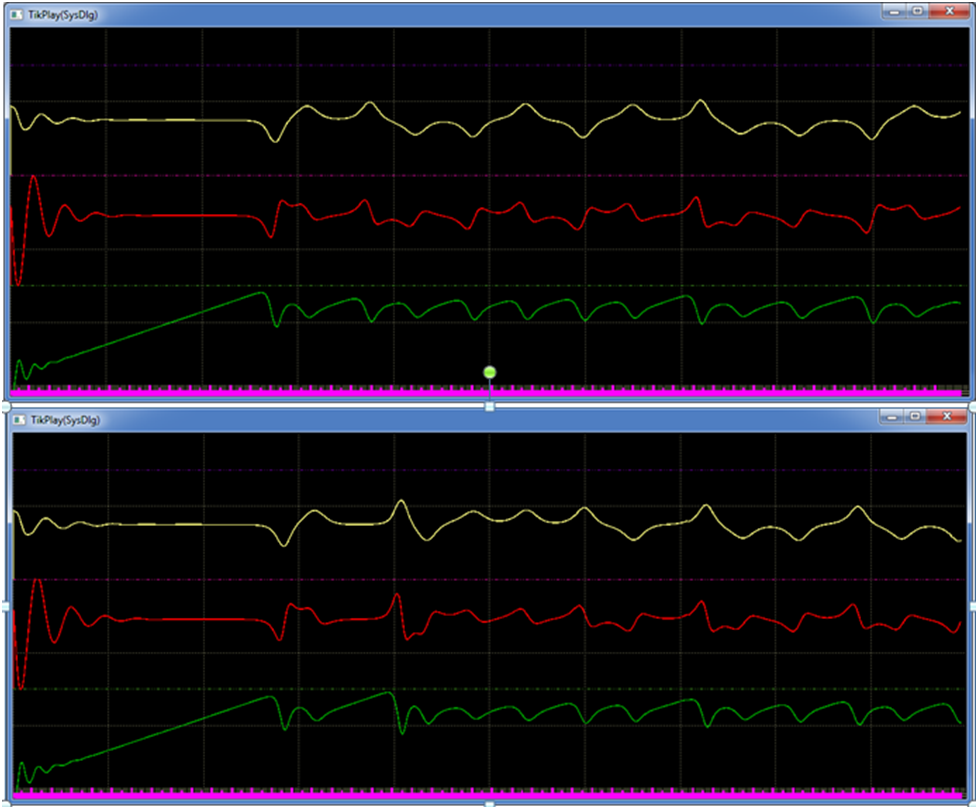
              Видно, что есть небольшие отличия даже между MATLAB и SimInTech, начиная где-то с 45-й секунды. При этом результаты в ВКПа достаточно существенно отличаются не только от первых двух пакетов, но и зависят от режима работы.             Но все же проблема не в разнице результатов (формы графиков). Для первых двух пакетов это может объясняться рядом причин - выбранными шагом, методом интегрирования и, возможно, сортировкой блоков. В ВКПа их (причин) всего-то две. Это или "мгновенное" изменение выходного значения блоками в момент его расчета при последовательном режиме работы с данными, или их запись в "теневой" буфер для использования на следующем шаге интегрирования уже в качестве нового текущего значения - параллельный режим работы с данными.

            Следует ли считать выявленную разницу в результатах программными ошибками? На мой взгляд любое отличие, а в программировании это особенно, должно быть объяснено. И лучше, когда оно не является следствием ошибок программирования. Разобраться с этой проблемой, как раз, и входит в обязанности программистов.  Или, как минимум, в "разборе полетов" должны принимать участие и они.

            Но для меня важнее все же совсем другое. Аттрактор Рикитаке однозначно выявил роль инерционности/задержек программных процессов.  Ведь, когда мы ее (задержку) фактически убрали (см. выше код на С++), то получили резко отличающийся результат. И его, кроме как влиянием задержек, а они появились именно в многоблочных реализациях, по-другому не объяснить. И проверить это, даже без использования упоминаемых программных пакетов,  весьма просто.  

            Для подобной проверки достаточно зациклить приведенный выше код (свой для каждого уравнения). И в одном варианте выходные значения пусть сразу становятся входными (тем самым имитируется последовательный режим работы ВКПа), а в другом - помещаются в буфер, становясь входными значения на новом цикле работы (параллельный режим работы ВКПа).

            Но те или иные выводы делать все же вам, хабровчане. Свои автор сделал достаточно давно и эксперименты с аттракторами их ни сколько не поколебали. При этом не сказать, чтобы замечания и "минусовки", полученные на предыдущую статью совсем меня не волновали... Но для меня важнее другой фактор - объективная оценка результатов экспериментов.

            Хотя их трактовка может быть весьма разнообразной. В том числе и субъективной. И тут почему-то вспомнилась фраза из  анекдота, которая звучит, кажется, так:  бороду-то сбрить можно, а вот с умищем-то, что делать? Но только не подумайте чего. Это всего лишь шутка, призывающая к объективности. И не более того.

Литература

1. Генераторы хаоса на ПЛИС. https://habr.com/ru/post/273915/

2. О программных ошибка на примере MATLAB и SimInTech. https://habr.com/ru/post/703244/