Силуэт

Силуэт — основная и наиболее мощная алгоритмическая макроконструкция языка ДРАКОН. В статье описан теоретический метод, позволяющий прояснить математические истоки конструкции силуэт.

На практике построение конструкции силуэт не представляет трудности и делается несколькими щелчками мыши. Но речь не об этом. Мы пойдем неочевидным путем и построим силуэт в два этапа. Сначала построим графическую заготовку классическим методом Ашкрофта-Манны. Затем с помощью специального приема преобразуем заготовку в силуэт.

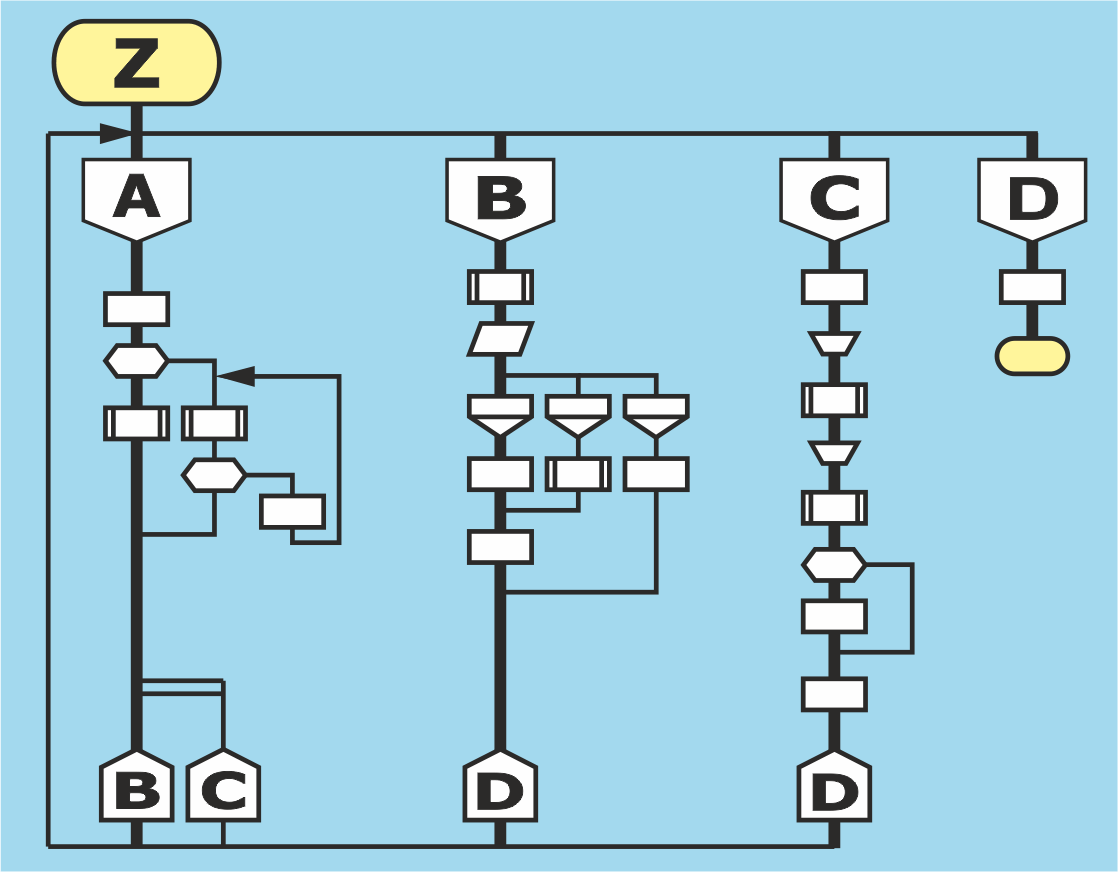
Рис. 1. Пример силуэта. Ветки В и С исполняются параллельно

Эдвард Ашкрофт и Зохар Манна

Шестьдесят лет назад, в 1961 году была опубликована статья Ашкрофта и Манна "The Translation of «Goto» Program to «While» Program", посвященная преобразованию неструктурной программы в структурную.

Статья стала классической, а метод получил название «метод введения переменной состояния».

Книга Эдварда Йодана (Edward Yourdon)

Далее изложение ведется, опираясь на книгу Йодана «Структурное проектирование и конструирование программ». Рассмотрим неструктурную программу на рис. 1 слева. Пронумеруем все блоки от 0 до 5 (рис. 1 справа).

Рис. 2. Пример, иллюстрирующий метод Ашкрофта-Манны

На рис. 2 слева показана неструктурная исходная программа. Справа та же программа, но все блоки пронумерованы от 0
до 5. Нумерация нужна, чтобы ввести переменную состояния.

Способ присваивания номеров совершенно произвольный. Обычно обозначают номером 1 первый исполняемый блок программы, а номером 0 — последний исполняемый блок.

Обратите внимание: на рис. 2 есть четыре наклонные линии, нарушающие эргономические требования к чертежу. На рис. 3 недочет исправлен.

Рис. 3. Та же программа. Наклонные линии заменены на вертикальные и горизонтальные.

Блок-преемник

Два соседних (соединенных стрелками) блока программы именуются как предшественник и преемник. Стрелка исходит из предшественника и указывает острием на преемника
(рис. 4).

Рис. 4. Что такое блок-преемник? Это блок, в который передается управление. Блок А имеет два преемника: блок B и блок C.

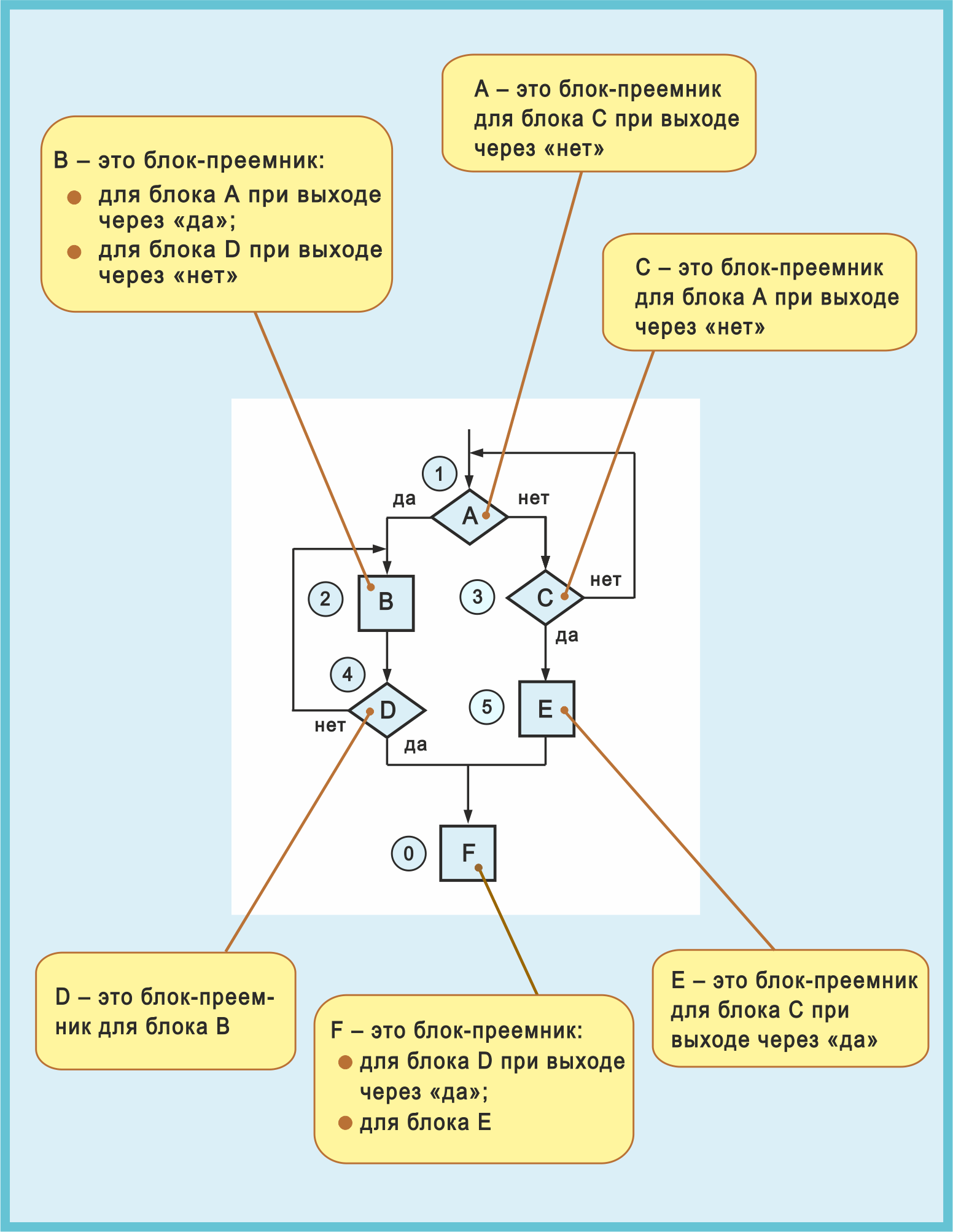
Рис. 5. Для всех блоков-предшественников и для всех выходов (да и нет) показаны блоки-преемники

На рисунке 5 комментарии в желтых рамках дают полное описание связей между предшественниками и преемниками.

Переменная состояния

В программу вводится новая переменная — переменная состояния. В методе Ашкрофта-Манны требуется переменная целого типа. Имя переменной произвольное. В нашем примере новая переменная обозначена через i (см. таблицу и рис. 6).

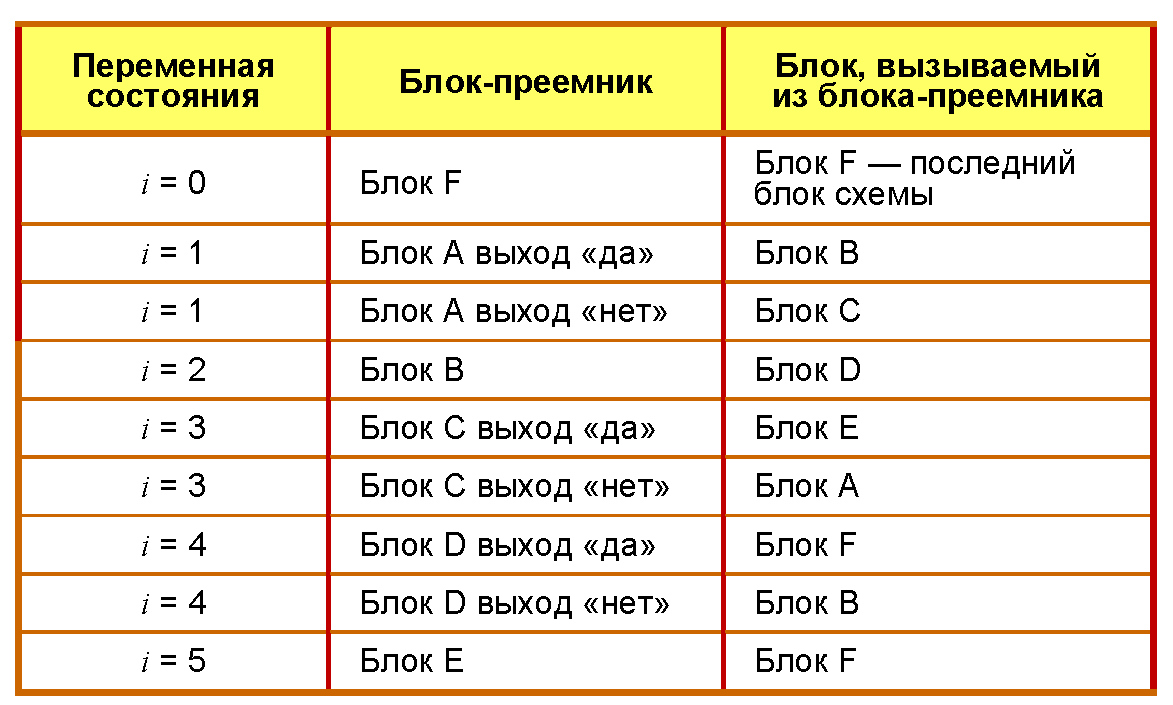
Рис. 6. Упрощенная схема. Переменная состояния i поочередно пробегает значения от 0 до 5. При этом она передает управление блокам исходной программы.

Преобразование Ашкрофта-Манны

Рис. 7. Схема Ашкрофта-Манны (графическая заготовка для силуэта)

В упрощенную схему на рис. 6 вводятся служебные блоки (справа на рис. 7). Они присваивают переменной i целое значение, указывающее номер блока-преемника.

Начальным значением переменной i выбрано число 1. Затем мы последовательно опрашиваем значения переменной i (слева на рис. 7), исполняем соответствующее действие, повторяем опрос i и т.д. В результате неструктурная программа на рис. 2 превращается в структурную на рис. 7.

Поясняя рисунок 7, Йодан отмечает:

Каждому блоку исходной схемы соответствует определенное состояние программы, т. е. ситуация, в которой либо проверяется логическое условие, либо выполняется некоторая обработка.

План рассказа

До сих пор я в качестве введения повторял хорошо известные вещи, чтобы получить схему Ашкрофта-Манны на рис. 7.

Введение позволяет перейти к основной части статьи и использовать схему Ашкрофта-Манны как заготовку для построения алгоритмической макроконструкции силуэт с помощью многошаговой серии преобразований.
Всего будет описано 19 шагов.

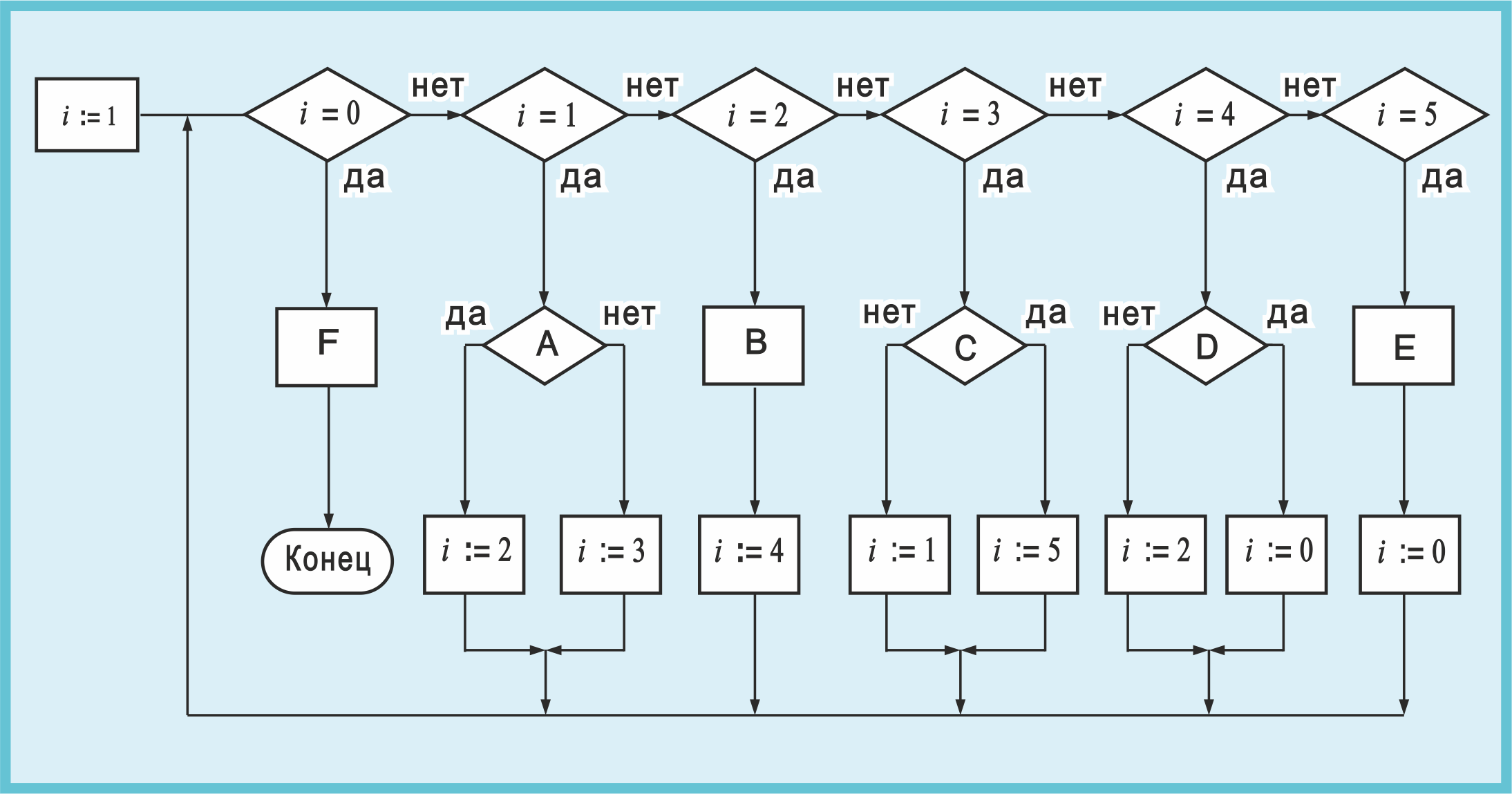
Рис. 8. Данная схема получена из схемы Ашкрофта-Манны на рис. 7 в результате поворота схемы на 90° и отражения сверху вниз

Шаг 1. Схема на рис. 7 поворачивается на 90° против часовой стрелки.
Шаг 2. Схема отражается сверху вниз. (Результат показан на рис. 8).

Наша цель – преобразовать схему Ашкрофта-Манны в схему силуэт

Рис. 9. Данная схема получена из схемы на рис. 8 с помощью серии преобразований

Шаг 3. Вертикаль, содержащая фигуру Конец, перемещена в крайнюю правую позицию.
Шаг 4. В логических блоках A, C, D выход влево заменен на выход вниз.
Шаг 5. Удалены три Т-образные линии в нижней части схемы, которые заменены вертикалями

Черновой силуэт

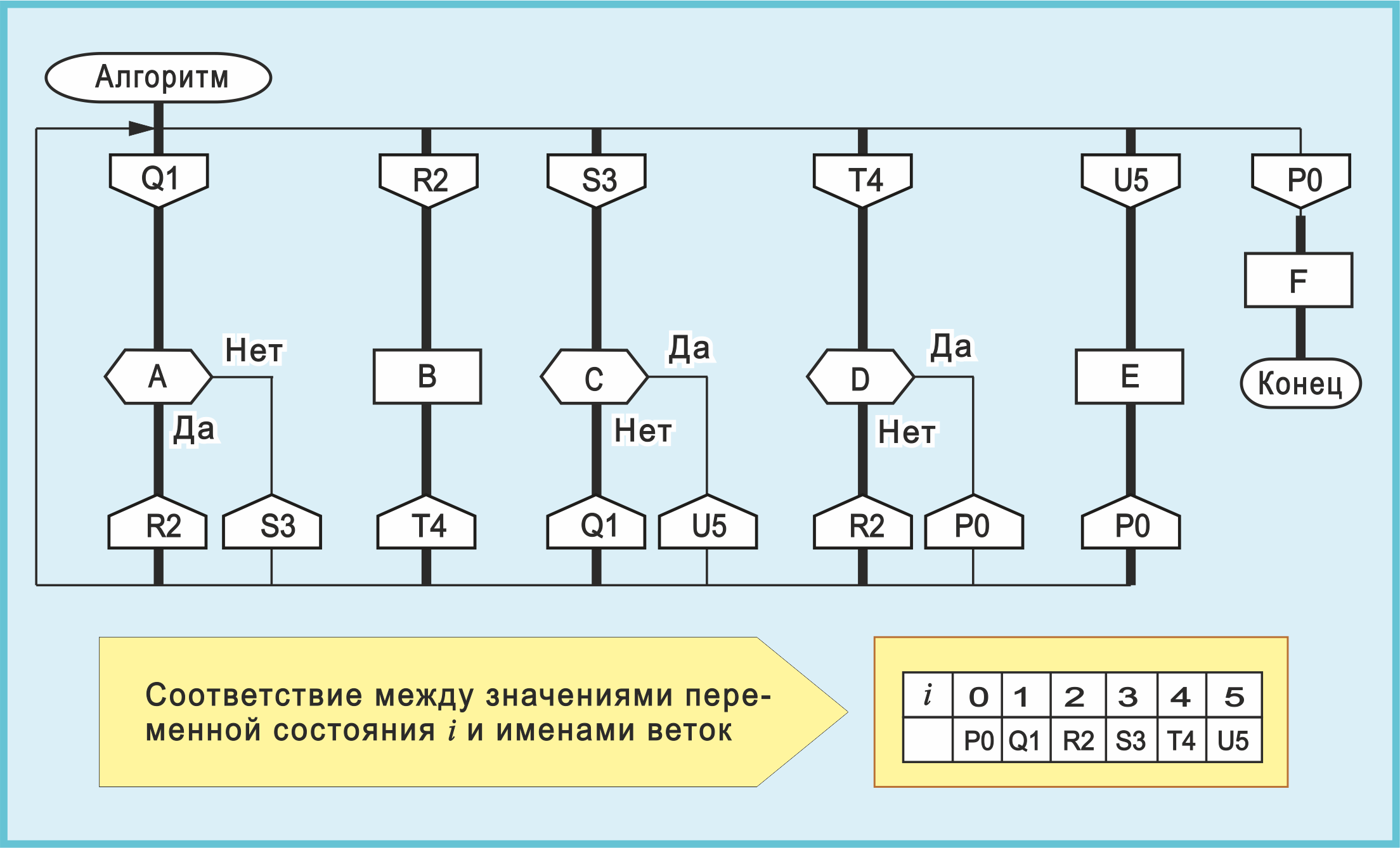
Рис. 10. Черновой силуэт получен из схемы на рис. 9 с помощью серии преобразований

В силуэте переменная состояния не нужна, о ней можно забыть. Значения переменной состояния превращаются в метки, символьные имена.

Шаг 6. Шампуры выделены жирной линией.
Шаг 7. Имя переменной состояния удаляется.
Шаг 8. Верхние фигуры на рис. 9 (ромбы) превратились
в иконы «Имя ветки».
Шаг 9. Нижние фигуры на рис. 9 превратились в иконы
Адрес.
Шаг 10. Внутри икон «Имя ветки» записываются метки,
обозначающие названия веток.
Шаг 11. Внутри икон Адрес записывается Имя ветки, куда
происходит передача управления в соответствии
с логикой работы алгоритма.

Объединение веток силуэта

Ветки силуэта можно объединять, удалять и разбивать на части.

Рис. 11. Частично исправленный черновой силуэт

На рисунке 10 показан формально правильный, но «плохой» силуэт — он скрывает структуру алгоритма. Чтобы исправить дефект, надо объединить некоторые ветки между собой.

На рисунке 11 сделано следующее (по сравнению с рис. 10):

1. объединены две ветки Q1 и S3. Икона Адрес S3 и икона «Имя ветки» S3 удалены;

2. объединены две ветки R2 и T4. Икона Адрес T4 и икона «Имя ветки» T4 удалены.

Опишем изменения в виде последовательности шагов.

Шаг 12. На рис. 11 удалены все иконы с надписью S3.
Шаг 13. К удаленному правому плечу ветки Q1 присоединена
ветка S3 с удаленной иконой «Имя ветки» S3.
Шаг 14. На рис. 11 удалены все иконы с надписью Т4.
Шаг 15. К удаленному низу ветки R2 присоединена ветка Т4
с удаленной иконой «Имя ветки» Т4.

Окончательно исправленный силуэт

Рис. 12. Силуэт с двумя веточными циклами

На рисунке 12 проведены следующие изменения (по сравнению с рис. 11):

1. объединены две ветки Q1 и U5. Икона Адрес U5 и икона «Имя ветки» U5 удалены;

2. веточные циклы Q1 и R2 выделены и обозначены черными треугольниками.

Опишем изменения в виде последовательности шагов.

Шаг 16. На рис. 12 удалены все иконы с надписью U5.
Шаг 17. К удаленному правому плечу ветки Q1 присоединена
ветка U5 с удаленной иконой «Имя ветки» U5.
Шаг 18. Веточные циклы Q1 и R2 обозначены черными
треугольниками.

Сравнение исходной схемы с силуэтом

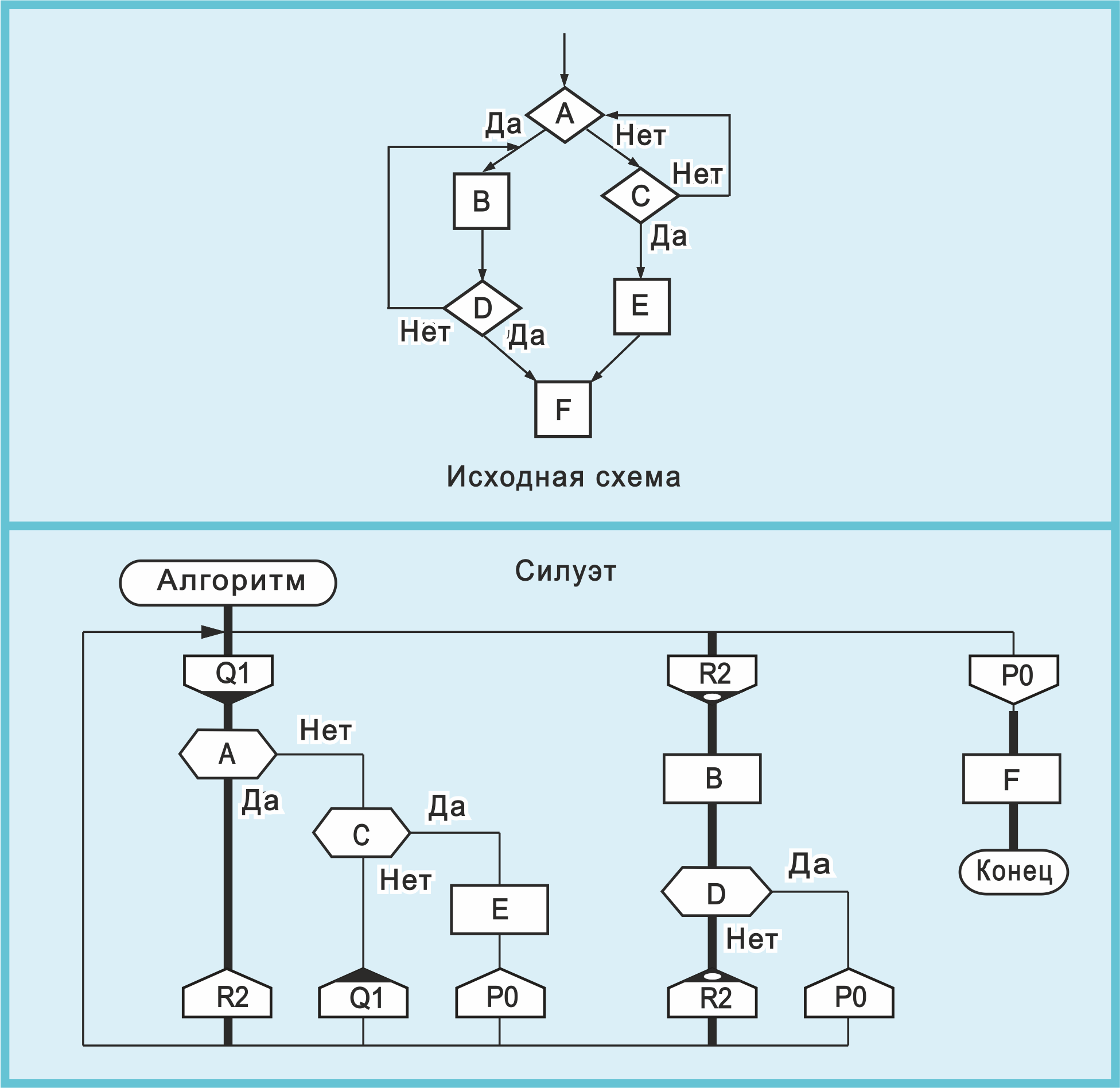
Рис. 13. На этом рисунке для удобства сравнения вверху показана исходная схема (рис. 2), а внизу абстрактный силуэт (рис. 12)

Сопоставляя два чертежа, можно отметить точное сходство между ними:

1. На исходной схеме показаны шесть блоков: A, B, C, D, E, F. Эти же самые блоки имеются на силуэте.

2. На исходной схеме есть три логических блока — три ромба: A, C, D. Эти же самые блоки имеются в силуэте, причем три ромба превратились в три иконы Вопрос.

3. На исходной схеме есть три блока обработки информации — три прямоугольника: B, E, F. Эти же самые блоки имеются в силуэте, причем прямоугольники называются иконы Действие.

4. На исходной схеме есть стрелки, обозначающие связи между иконами по принципу «предшественник-преемник». Те же самые связи имеются в силуэте, только без стрелок. Например, в исходной схеме есть связь E-F, которая в силуэте превращается в связь E-P0-P0-F, причем элементы P0 не искажают сигнал.

Сказанное означает, что силуэт точно отображает обработку информации в исходной схеме.

Силуэт со смысловыми надписями

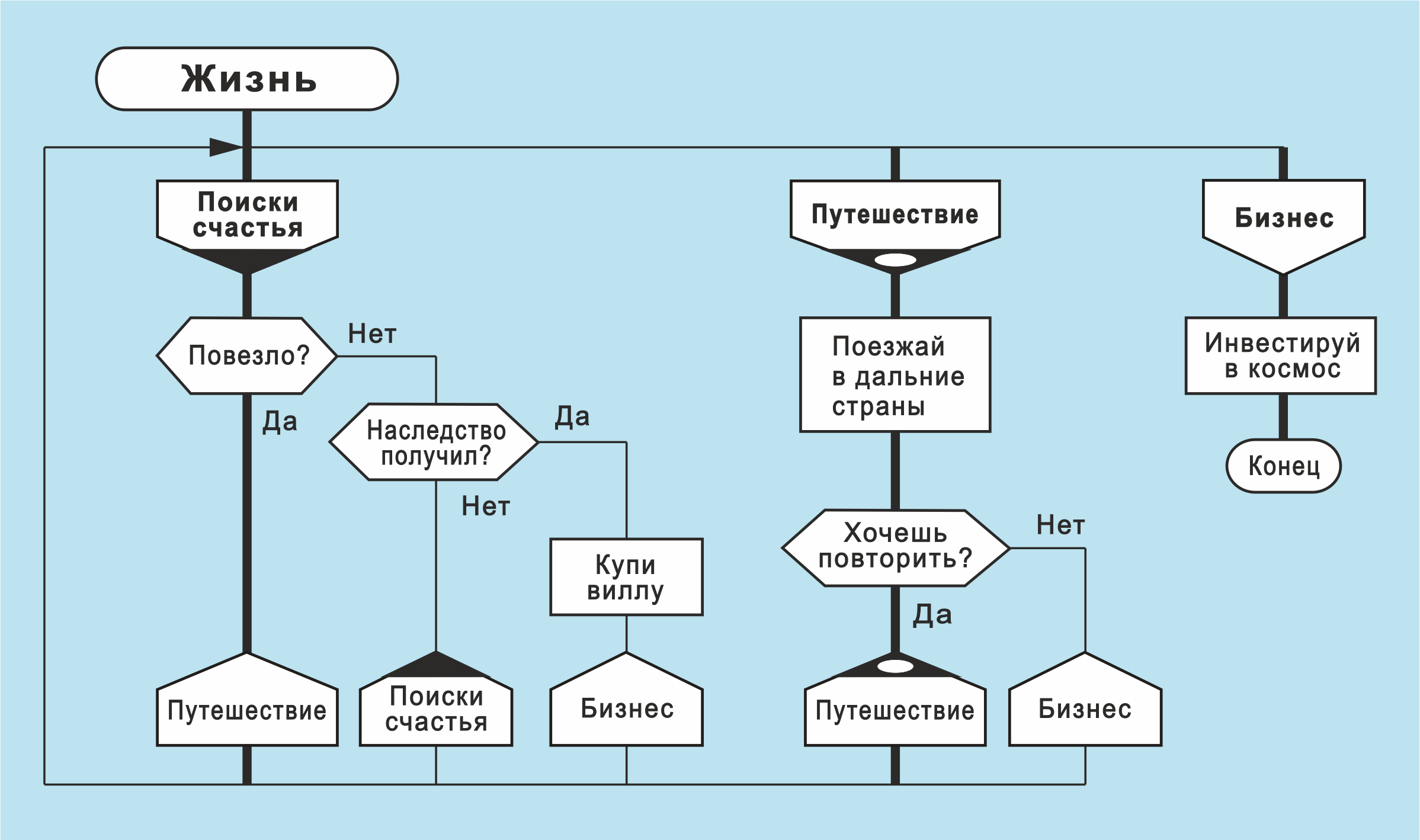
Рис. 14. Силуэт со смысловыми надписями

Смысловой силуэт (по сравнению с абстрактным силуэтом на рис. 12 и 13) обладает новым свойством. Он должен удовлетворять картографическому критерию, например, принципу «чем правее, тем хуже», (который действует локально внутри каждой ветки и не распространяется за ее пределы).

На рис. 14 этот принцип нарушен в ветке «Поиски счастья». В самом деле, маршрут «Наследство получил? Нет» должен находиться справа, а он по ошибке оказался в центре ветки.

Чтобы исправить ошибку, надо применить математическую операцию «рокировка» к иконе Вопрос «Наследство получил?»
Результат рокировки показан рис. 15.

Силуэт, удовлетворяющий картографическому критерию

Рис. 15. Силуэт, удовлетворяющий требованиям

Шаг 19. На рис. 15 выполнена рокировка в иконе Вопрос
«Наследство получил?»

Заключение

Цель статьи — выявить математические истоки алгоритмической макроконструкции «силуэт». На самом деле, истоков несколько: визуальный аксиоматический метод, визуальное логическое исчисление, визуальная алгебра логики и др. В статье рассмотрена только преобразование схемы Ашкрофта-Манны в силуэт.

Статья делится на две части. Вводная часть описывает метод Ашкрофта-Манны, опирающийся на введение переменной состояния и показана на рисунках 2–7.

Основная часть использует схему Ашкрофта-Манны как графическую заготовку, которая превращается в макроконструкцию силуэт с помощью специального приема,
состоящего из 19 шагов и показанного на рисунках 8–15.