Как им это удалось?

Расшифровка таблички
Для начала расшифруем саму табличку. Она маркирована как YBC 7289 (сокращённо от «7289-й предмет из Вавилонской коллекции Йеля, Yale Babylonian Collection»). На табличке показан квадрат, его диагональ, а рядом написаны числа. Вот её стилизованная версия из книги Episodes from the Early History of Mathematics Асгера Обое.
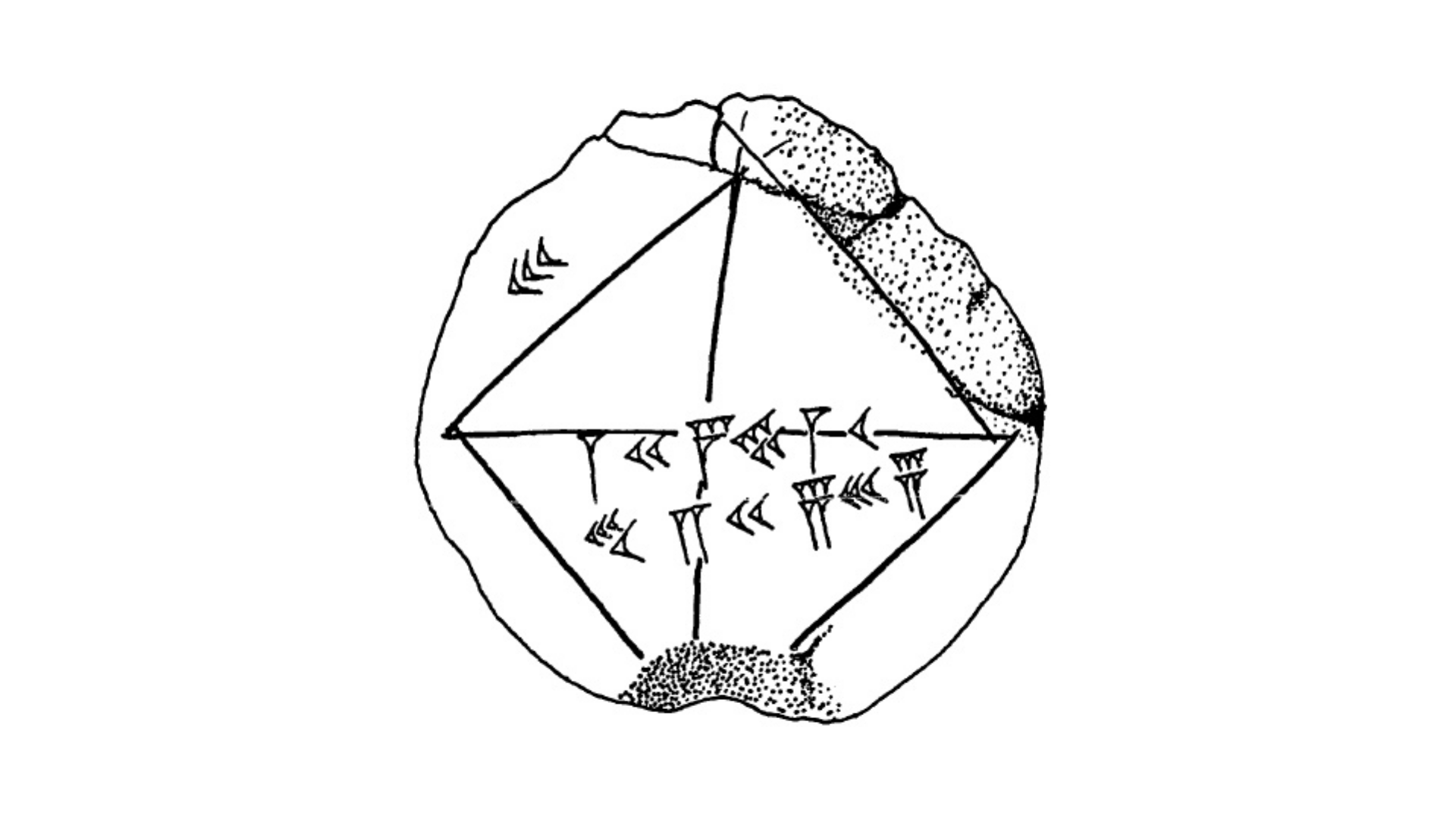
Как следует из теоремы Пифагора, длина диагонали единичного квадрата равна √2. Давайте разберёмся с символами!
На табличке указаны числа, записанные в виде вавилонских клинописных нумералов. Они означают 1, 24, 51 и 10.

Так как вавилоняне использовали систему счисления по основанию 60 (также называющуюся шестидесятеричной), число 1,24 51 10 в десятичной системе означает 1,41421296296.
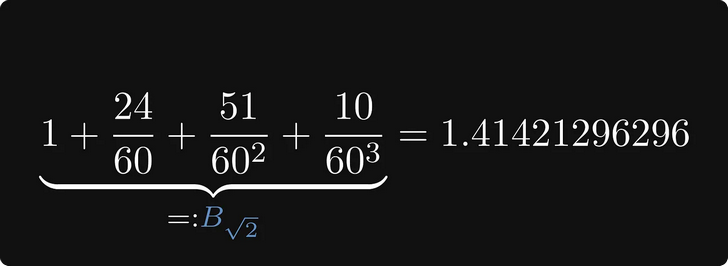
Это совпадает со значением √2 до шестого знака после запятой, то есть соответствует точности в 99,9999%!

Точность вычислений поражает. Попробуйте воссоздать её без калькулятора, на бумаге, это не так уж просто!
И мы расскажем, как им это удалось.
Вавилонский алгоритм вычисления квадратного корня
Сейчас я буду изображать фокусника: сначала покажу алгоритм, а затем отдёрну занавес и объясню его.
Мы начинаем с выбора числа x₀ между 1 и √2. Я знаю, это кажется случайным, но не будем торопиться. Например, таким числом может быть 1,2, что станет нашей первой аппроксимацией.
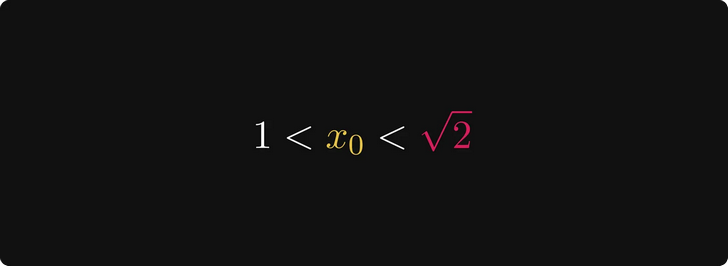
Исходя из этого, 2/x₀ больше √2.
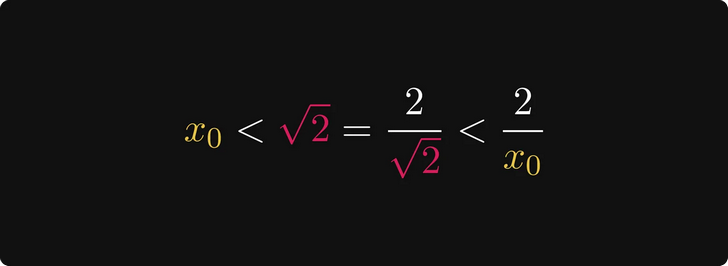
Следовательно, интервал [x₀, 2/x₀] включает в себя √2.
Из этого следует, что средняя точка интервала [x₀, 2/x₀] является более точной аппроксимацией значения √2. Как видно на рисунке ниже, она существенно лучше!
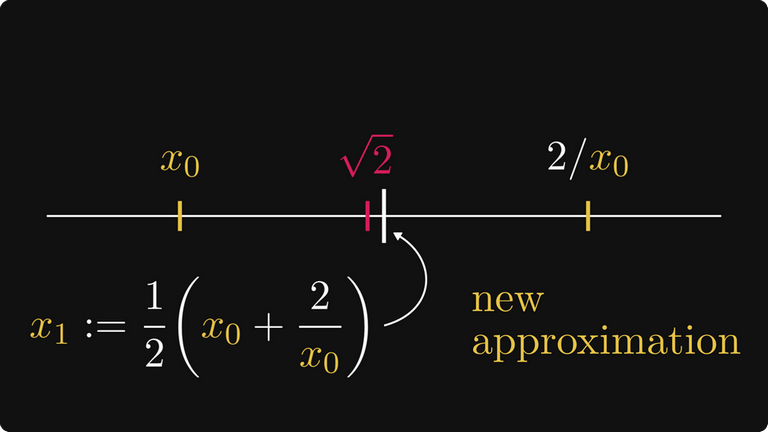
Давайте определим из этого x₁.
Развивая эту тему, мы можем определить последовательность аппроксимации, беря средние точки таких интервалов.

Вот несколько первых членов последовательности. Даже третий член уже является на удивление хорошей аппроксимацией.

Если мы нанесём эти числа на диаграмму рассеяния, то спустя несколько шагов нам уже практически понадобится микроскоп, чтобы увидеть отличия от √2.
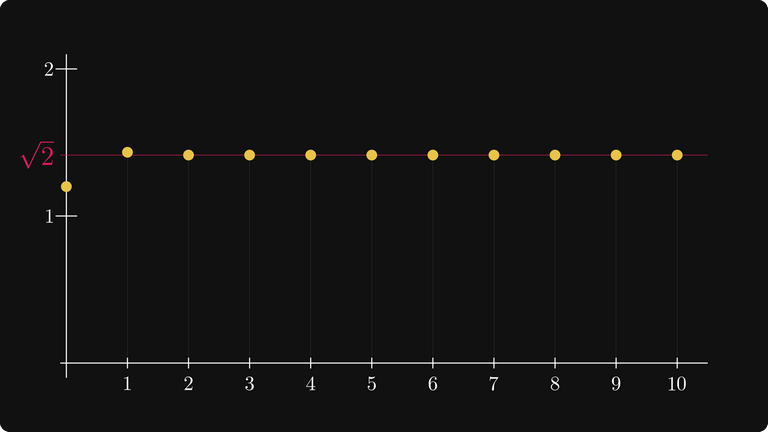
Как видите, это сходится к √2 чрезвычайно быстро.
Но насколько быстро?
Погрешность вавилонской аппроксимации
Погрешность между этой аппроксимацией и значением √2 определяется просто как расстояние между ними, замеренное по абсолютному значению их разности. Например, погрешность нашего первого предположения e₀ задаётся следующим образом:

Каким бы малым или большим ни было e₀, мы можем использовать её для оценки последующих погрешностей.
Давайте займёмся алгеброй и посмотрим, как e₀ относится к e₁! Сначала выразим e₁ в виде дроби.

Тогда поскольку мы выбрали x₀ больше единицы, то можем выразить его в членах e₁. Так как числитель e₀ возведён в квадрат, наша задача проста.

Повторяя эти рассуждения, мы получаем, что сходимость очень быстра, даже быстрее экспоненциальной!
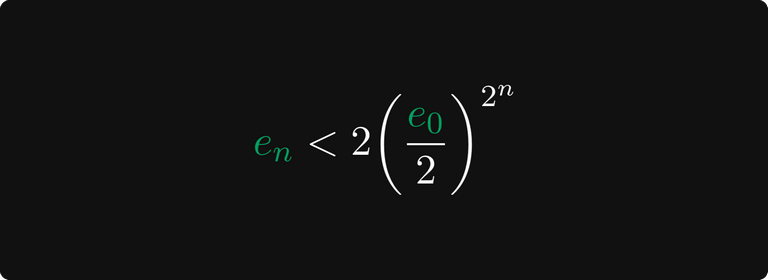
Повезло ли вавилонянам, или они угодили в самую точку?
На самом деле, второе. Настало время поднять занавес!
Метод Ньютона-Рафсона
Давайте перефразируем задачу аппроксимации квадратного корня из двух. Вместо того, чтобы вычислять функцию f(x) = √x в заданной точке, попробуем найти корень (положительный) f(x) = x² — 2. (Который, как оказывается, тоже равен √2.)
Существует ли обобщённый метод решения такой задачи? Да, это метод Ньютона-Рафсона. Чтобы показать, как он работает, давайте приблизим корень f(x).
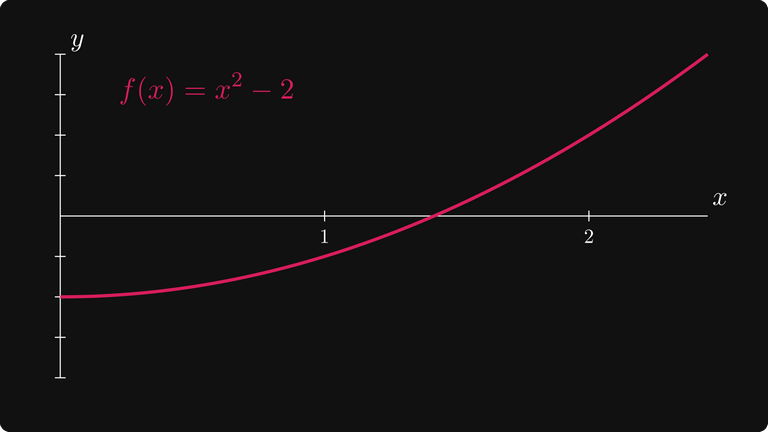
График f(x) = x² — 2
Как мы можем переместиться от нашей первоначальной догадки x₀ к корню?
Например, можно следовать по направлению касательной и посмотреть, где она пересекает ось X. Поскольку угол касательной определяет производная, это пересечение можно сразу вычислить. Я покажу, как это сделать.
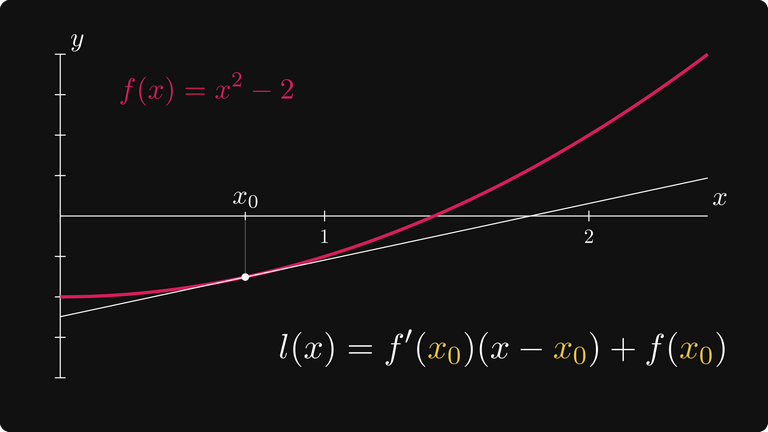
Уравнение касательной задаётся следующим образом.

Приравняв его к нулю и решив, мы получим точку, в которой касательная пересекает ось X.

Таким образом, выбрав следующую догадку x₁ в качестве этой точки пересечения, мы получим более точную (надеемся) аппроксимацию.
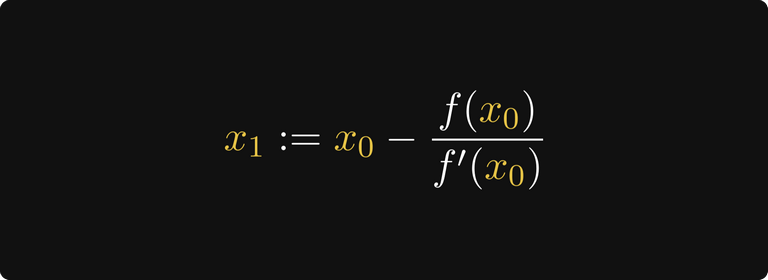
Вот и всё! На основании этой идеи мы можем определить рекурсивную последовательность.
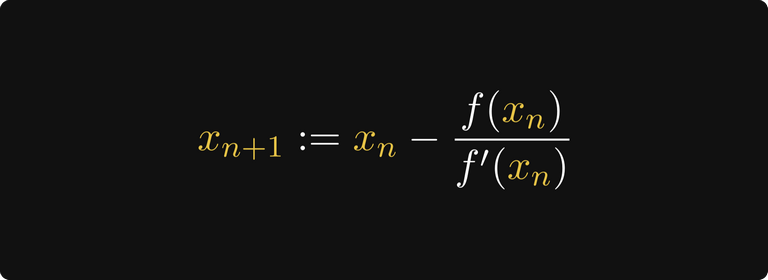
Это называется методом Ньютона-Рафсона. Вот следующий шаг. Как видите, третий шаг находится почти в √2.

Остаётся один важный вопрос: такой ли способ применили вавилоняне? Да, и вот почему.
Метод Ньютона-Рафсона и вавилонский алгоритм
В предыдущем примере мы решили найти корень f(x) = x² — 2. Давайте найдём явную формулу рекурсивной последовательности, заданной методом Ньютона-Рафсона. Её производную легко вычислить, так что мы готовы.

Применив немного алгебры, мы можем прийти к не особо удивительному выводу.

Следовательно, вавилонский алгоритм — это частный случай метода Ньютона-Рафсона!
Мы помним, что сходимость в этом конкретном случае крайне быстрая. Справедливо ли это в общем случае? Если нам повезёт.
Скорость сходимости
Если не вдаваться в подробности, сходимость и её скорость зависят от локального поведения функции.
Например, если f(x) дважды дифференцируема, то член погрешности для n-ного элемента может быть описан членами производных и квадратом (n-1)-ной погрешности.
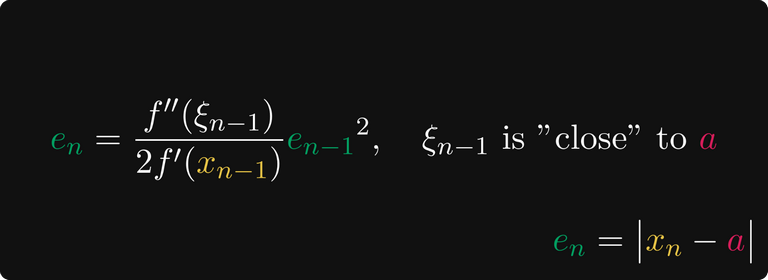
(Если вам интересны подробности, то доказательство есть в Википедии.)
В частности, если производные «ведут себя хорошо» (то есть первая производная отделена от нуля, а вторая производная ограничена), то скорость сходимости квадратичная.

Если функция «ведёт себя хорошо»
Квадратичная сходимость истинна не только для поиска квадратного корня двух аппроксимацией положительного корня f(x) = x² — 2, но и для широкого спектра функций.
Недостатки
К сожалению не всё так идеально. Метод Ньютона-Рафсона может давать серьёзные сбои в довольно часто встречающихся случаях, к тому же имеет множество недостатков.
Например, если функция рядом с корнем «плоская», то сходимость будет мучительно медленной. Один из таких случаев показан ниже.

Это происходит, когда корень имеет большую повышенную неоднозначность, то есть производные тоже равны нулю. Кстати о производных, в отличие от случая с квадратным корнем вавилонян, их может быть сложно вычислить, из-за чего этот метод оказывается неприменимым.
Более того, весь процесс сильно зависит от первоначальной догадки: итерация может сойтись к неверному корню или даже разойтись.
Вывод
То, что древние вавилоняне смогли вычислить √2 до шестого знака после запятой, достаточно удивительно. Эта точность вызывает большое уважение, особенно учитывая, что она была достигнута почти четыре тысячи лет назад и вычисления выполнялись вручную.
Как оказалось, им не просто повезло; они обнаружили особый случай мощного метода, способного аппроксимировать корень широкого спектра функций. Он стал известен под названием «метод Ньютона-Рафсона».
Принцип прост:
- Предполагаем первоначальное значение x₀
- Временно заменяем функцию касательной к ней в x₀
- Определяем, где касательная пересекает ось X
- Используем это пересечение x₁ в качестве новой начальной точки процесса.
Если функция ведёт себя достаточно хорошо (то есть её производная локально отделена от нуля, а вторая производная ограничена), то сходимость происходит чрезвычайно быстро: именно поэтому вавилоняне смогли достичь «наивысшей в древнем мире вычислительной точности».
Комментарии (62)

freeExec
00.00.0000 00:00+65Что-то я не понял чему тут удивляться. Если бы на табличке была формула вычисления квадратного корня из любого числа то да. А так, одиночное вычисление корня из 2 занятие на 1 день методом перебора.
1.5 * 1.5 = 2.25 — перебор
1.4 * 1.4 = 1.96 — недобор
1.42 * 1.42 = 2.0164
1.41 * 1.41 = 1.9881
и т.д.vlanko
00.00.0000 00:00Я начинал вычисления с бинарного поиска, потом метода Ньютона, но Вавилонский получился самым быстрым по вычислительным ресурсам.

linchk
00.00.0000 00:00Не забывайте, что четыре тысячи лет назад не было позиционной системы счисления и сама система была 60ричная. Так что даже умножение было не тривиальной задачей.

freeExec
00.00.0000 00:00Почему не тривиально? Тоже умножение столбиком будет работать. Сейчас вполне на листочке можно считать хоть в двоичной, хоть в шестнадцатеричной системе. Просто это кажется несколько не привычно, но если ты никогда другого не видел, то проблем не вызовет.
Вот мы умножаем 4*3 и у нас получается 12.
Но если у нас 6-ричная система, то будет 20 (потому что два полных "цикла" по 6).
Или 8-ричная, то будет 14 (8 даёт нам новый разряд и ещё 4 остаётся).
linchk
00.00.0000 00:00Был не прав. Система у Вавилонян была позиционной - это сильно упрощает расчёты. Судя по источникам -изначально не было понятия 0, что вносило некоторую неоднозначность в цифровую запись. А вот известны ли были приёмы деления и умножения в столбик - я пока упоминаний не нашёл.

Radisto
00.00.0000 00:00+71Не хочу никого обижать, но я так и не понял из описания, как это сделали вавилоняне.

commanderxo
00.00.0000 00:00+4Вот именно, например интересно как выглядело деление "в столбик" в вавилонской клинописи. Судя по записи 24 и 51 это гибрид десятичной и шестидесятеричной систем.

anonymous
00.00.0000 00:00НЛО прилетело и опубликовало эту надпись здесь

Radisto
00.00.0000 00:00+1Реальные возможности того времени в области математики практически ничем не отличались: голова и то, чем и на чем можно писать. Опыта было меньше и возможностей обмена им. Ну и возможностей просчета и перебора огромных массивов чисел тоже не было без компьютеров. Но многие теоремы из геометрии были известны уже тогда. Все таки в математике огромную роль играют мозги, врожденные способности, а они не очень зависят от того, где и когда человек родился. Мы с палеолита физиологически мало изменились

anonymous
00.00.0000 00:00НЛО прилетело и опубликовало эту надпись здесь

unC0Rr
00.00.0000 00:00Тогда предположите каким образом действовал Галей!
Галлей элементарно воспользовался историческими данными о пролётах комет и заметил одну, которая прилетала через равные промежутки времени. Из математики потребовалась только способность подсчитать разность между датами в прошлом.

celen
00.00.0000 00:00+7Интересно, как им удалось вычислять 2/n. У них, вроде бы, не было аппарата рациональных дробей с основанием, не делящим 60^k в нашем понимании; между тем, последовательность порожденных методом Ньютона рациональных приближений корня из двух выглядит так:
3/2 , 17/12, 577/408 , 665857/470832...
Если бы аппарат записи произвольных рациональных дробей у них был, они непременно записали бы 577/408 на такой табличке.
Хотя последнее, сверхточное приближение дает нам целых 11 знаков, предпоследнее - 577/408 - дает всего 5. А вавилоняне насчитали 6 знаков, что больше, чем дало бы им, если бы они остановились на 577/408 и приблизительно выразили полученное в 60-ричной системе счисления. Это значит, что они смогли скорректировать квадратный корень более точно, чем 577/408. Возможно, они использовали метод Ньютона, но последний знак они почти наверняка получили прямым перебором всех шестидесятичных дробей с тремя знаками с аккуратным возведением их в квадрат.

lgorSL
00.00.0000 00:00+2Достаточно бинарного поиска. Число в квадрате либо больше двух, либо меньше. 60 < 64 = 2^6, на каждую "цифру" в 60-ричной системе счисления достаточно шести проверок.

BaLord
00.00.0000 00:00+1Да никто не решала перебором, в до н.э. они в основном рисовали на песке и прикидывали на песке, посмотрите пожалуйста мой ответ, есть графическое решение данного метода, просто берем квадрат с большими сторонами и меряем диагональ квадрата, чем больше по размерам квадрат тем диагональ можно посчитать с большей точностью.
vlanko
00.00.0000 00:00Указанный пример основан на числе 1,2. Как точно считали вавилоняне - нужно разбираться.

Alex500IS
00.00.0000 00:00+14Что мы видим, на табличке написаны цифры и все ...
Все остальное притянуто за уши и придумало ради "открытия" ...
baldr
00.00.0000 00:00+5В общем-то, да, ничто не мешало взять длинные веревки и построить квадрат со стороной в несколько метров, а потом измерить диагональ.

amphasis
00.00.0000 00:00+24С точностью до 6-го знака? Это, грубо говоря, надо было построить идеальный километровый квадрат и измерить диагональ с точностью до миллиметра.

baldr
00.00.0000 00:00+13Согласен, километр - это даже для шумеров многовато.
грубо говоря
Вообще говоря, 700 метров тогда уж. Но тоже много.
грубо говоря


ZiggiPop
00.00.0000 00:00+6Если бы про вавилонскую систему счисления было бы известно мало — то так оно и было бы. Но на самом деле историки знают про вавилонскую математику очень много благодаря эдаким "таблицам Брадиса" — большому количеству сохранившхся справочных математических материалов на глиняных табличках, которые прекрасно пережили тысячелетия. Например, таблица с пифагоровыми тройками или табличка со своей формулировкой теоремы Пифагора.

Samedi_Da_Kapa
00.00.0000 00:00+8Вопрос по первому шагу:
Мы начинаем с выбора числа x₀ между 1 и √2.
Если я не знаю, чему равен корень из двух, то я могу взять 1,5. И уйти от точки корня. Тут можно справедливо возразить, что это легко проверяется возведением в степень. Но тогда и возникает вопрос - для чего мучаться с хитрыми алгоритмами, если можно просто взять и сделать нахождение перебором. Это более просто и интуитивно.
Соответственно вопрос - есть ли где-то описание того, что вавилоняне действительно использовали этот алгоритм? Или это просто предположение основанное на том, что на табличке есть число близкое к реальному значение?
Dimsml
00.00.0000 00:00+1На Вики сказано, что да, неизвестный Вавилонский математик нашёл корень из двух, но неизвестно как. При этом есть описание того как считали приблизительную длину гипотенузы похожим методом, а там же нужно корень искать, так? Так что получается что какие-то корни они похом методом искали, могли искать и этот.
Ссылаются вот на эту бумажку, я её коротко просмотрел и там честно написано, что никаких доказательств именного того, что кто-то считал корень из двух этим методом нет, но у вавилонян были готовые таблицы с часто употребляемыми числами, например в одной из табличек указано значение на которое надо умножить сторону квадрата чтобы получить диагональ. Т.е. кто-то уже взял готовый квадрат со стороной один, посчитал что диагональ будет равно 1 уможенное на этот коэффициент.
Т.е. у нас есть готовое значение, которое кто-то посчитал (подобрал?), но нет именно записей о том как это сделано? Просто сделан вывод что раз для подсчёта диагонали надо как-то подобрать значение корня, то видимо был какой-то метод и его могли применить тут?
Т.е. в результате получается что были таблицы с готовыми значениями корня из двух или диагонали квадрата со стороной 1, например, но нет записей о том, как именно это считалось?
Я правильно понял? Призываю математиков, которые хорошо знают предметную область на английском.
https://www.sciencedirect.com/science/article/pii/S0315086098922091/pdf

ZiggiPop
00.00.0000 00:00+1Очевидно, благодаря тому, что вавилоняне оставили и описания своих алгоритмов, а не только их результатов. Представленная табличка — всего лишь шпаргалка с готовым результатом, но есть и таблички с описанием итеративного метода поиска квадрата из двух.

edo1h
00.00.0000 00:00+1можно пруф?

ZiggiPop
00.00.0000 00:00Although YBC 7289 is frequently depicted (as in the photo) with the square oriented diagonally, the standard Babylonian conventions for drawing squares would have made the sides of the square vertical and horizontal, with the numbered side at the top.[4] The small round shape of the tablet, and the large writing on it, suggests that it was a "hand tablet" of a type typically used for rough work by a student who would hold it in the palm of his hand.[1][2] The student would likely have copied the sexagesimal value of the square root of 2 from another tablet, but an iterative procedure for computing this value can be found in another Babylonian tablet, BM 96957 + VAT 6598.[2]

victor_1212
00.00.0000 00:00+4таки что же именно написано на BM 96957 и др.?
просмотрев ссылки (те что на поверхности)
всключая статью [2] - "Square Root Approximations in Old Babylonian Mathematics:YBC 7289 in Context" David Fowlerm, Eleanor Robson (1998), ничего похожего на общий алгоритм там не видно, более точно цитата из этой вполне приличной статьи:
"... there is still no direct evidence—by which we mean explicit instructions in the course of a mathematical solution—for the use of more than the first step of the procedure",
пока вывод можно сделать один - в части алгоритма, это скорее всего современные фантазии, знание в Вавилоне было эмпирическим, большое количество отдельных фактов, типа сотни известных пифагоровых троек, но никаких обобщений на общий случай, самое понятие доказательства, или математической абстракции, тем более алгоритма совершенно неизвестно,
Пифагор в молодости провел несколько лет в Вавилоне, в том числе общался со жрецами носителями этого знания, он вероятно одним из первых понял недостатки эмпирического знания, вернувшись домой основал свою школу в которой именно логическое доказательство было целью и смыслом, так собственно и была создана математика в ее современном понимании, т.е. основанная на логических рассуждениях

amkartashov
00.00.0000 00:00+1Надо смотреть более поздние источники.
2017 год https://www.researchgate.net/publication/319286288_Plimpton_322_is_Babylonian_exact_sexagesimal_trigonometry#pf19 стр.8:
The procedure used in these examples is well understood; Friberg (2007, 305) calls it the square side rule but it is perhaps more familiar as Heron’s method.
А вот страница, на которую он ссылается (2007 год): https://books.google.no/books/content?id=sOiHePN7cW8C&hl=no&pg=PA305&img=1&zoom=3&sig=ACfU3U3Huu1rTMmZsrpwXmgaCu4WklADvw&w=1280

ZiggiPop
00.00.0000 00:00+3>ничего похожего на общий алгоритм там не видно
У Fowler and Robson на 371-й странице приводится метод вычисления диагонали, который использует писец таблички BM 96957, в переводе на современную алгебру. Причем даже в самом вавилонском тексте так прямо и указывается — "это метод".
A gate, of height 1/2 rod 2 cubits, and breadth 2 cubits. What is its diagonal? You: square 0;10, the breadth. You will see 0;01 40, the base. Take the reciprocal of 0;40 (cubits), the height; multiply by 0;01 40, the base. You will see 0;02 30. Break in half 0;02 30. You will see 0;01 15. Add 0;01 15 to 0;40, the height. You will see 0;41 15. The diagonal is 0;41 15. The method.
Да, это вполне эмпирический метод вычисления диагонали, но при этом достаточно точный, значение получается с точностью до третьего знака в десятичной системе счисления (у нас изначальные значения представлены в шестидясетиричной дроби). Вычисления по этому методу дают 0,6875 стержня (не знаю как правильно перевести меру длинны rod), посчитал сам, против 0,687184271, полученным при помощи теоремы Пифагора и калькулятора.
Но по сути этот способ вычисления в частном случае при равных сторонах "ворот" представляет собой просто Вавилонский метод, или метод Герона, при помощи которого корень аппроксимируется с любой необходимой точностью:
edo1h
00.00.0000 00:00+1У Fowler and Robson на 371-й странице приводится метод вычисления диагонали, который использует писец таблички BM 96957, в переводе на современную алгебру
Насколько интереснее и полезнее была бы статья, если бы в ней это было разобрано!

amkartashov
00.00.0000 00:00+2Если я не знаю, чему равен корень из двух, то я могу взять 1,5. И уйти от точки корня.
Там сходимость к корню из двух для любого начального x > 0.

eversyt
00.00.0000 00:00+1Вам достаточно возвести 1,5 в квадрат и сравнить с 2 :) Кроме того метод сходится достаточно хорошо, достаточно взять заведомо меньшее число, ту же единицу.

StjarnornasFred
00.00.0000 00:00А сейчас существует простой и школьнико-понятный способ извлечения квадратного или вообще любого корня из произвольного числа? Ну, типа как умножение и деление в столбик.

baldr
00.00.0000 00:00+4Да, существует - это метод перебора как и указали выше во втором комментарии. Кстати, деление в столбик - это тоже разновидность перебора.
Есть способ немного ускорить этот процесс - это, как ни странно - таблицы с предвычисленными значениями до какой-то степени точности. Если нужна точность выше - то берутся граничные значения из таблицы и продолжаем подбирать дальше. То же и с делением.
Насколько я знаю, все FPU примерно так и работают - у них на аппаратном уровне зашиты большие таблицы для ускорения многих операций.

ZiggiPop
00.00.0000 00:00+1Вот вам прям с вычислением в столбик:
ВЫЧИСЛЕНИЕ КВАДРАТНОГО КОРНЯ. ФОРМУЛА ДРЕВНЕГО ВАВИЛОНА - YouTube
Radisto
00.00.0000 00:00Для задавшего вопрос выше, не для автора поста - описанный в видео метод - приближенный, а так как итерации не предполагаются, то точность не увеличивается. Там описана одна итерация и соответственно точность невысока, хотя на практике вавилонянам была достаточна. В примере из видео уже во втором знаке после запятой цифра не та (если не округлять). Это я на всякий случай, вдруг нас школьники читают и пойдут "побеждать" учителей. Так-то читатели уже наверное проверили

AxeFizik
00.00.0000 00:00Да — перебор, возможно с бинарным поиском.
Мне, помню, на алгебре его показывали классе в шестом-седьмом, всё было понятно. Правда учительница сразу сказала, что это способ для тех у кого слишком много свободного времени

frol_aleksan
00.00.0000 00:00Есть. Метод Герона. Формула проста: Xn+1 = (Xn+(A/Xn))/2
A - число из которого извлекаем корень
за первое Xn принимается любое целое положительное число, хоть 1 (но чем дальше оно будет от конечного результата, тем больше итераций потребуется), далее подставляется число, полученное на предыдущем шаге.

speshuric
00.00.0000 00:00А ещё это лучшее рациональное приближение, т.е. нет такого рационального числа с меньшим знаменателем, которое ближе к корню из 2, чем данное. То, что это приближение лучшее легко увидеть из того, что по алгоритму получается непрерывная цепная дробь.

1e100
00.00.0000 00:00ChatGPT тоже знает такой алгоримт:
The Babylonian algorithm (also known as the Heron's method) is an iterative method for approximating the square root of a number. To find the square root of 2 using this algorithm, we start with an initial guess and iteratively refine it until we reach an acceptable level of accuracy. Here are the steps:
Choose an initial guess for the square root of 2, such as 1.
Compute the average of the guess and 2/guess, i.e., (guess + 2/guess)/2.
Use the result from step 2 as the new guess.
Repeat steps 2 and 3 until the guess is close enough to the true square root of 2.
To determine when the guess is close enough to the true square root of 2, we can choose a tolerance level and stop iterating when the difference between the guess and the true square root of 2 is less than that tolerance level. For example, if we choose a tolerance level of 0.0001, we can stop iterating when |guess^2 - 2| < 0.0001.
Here is an example of how the algorithm works:
Guess = 1
New guess = (1 + 2/1)/2 = 1.5
New guess = (1.5 + 2/1.5)/2 = 1.41666666667
New guess = (1.41666666667 + 2/1.41666666667)/2 = 1.41421568627
New guess = (1.41421568627 + 2/1.41421568627)/2 = 1.41421356238
At this point, the difference between the guess and the true square root of 2 is less than 0.0001, so we can stop iterating and conclude that the square root of 2 is approximately 1.41421356238.

BaLord
00.00.0000 00:00Зачем такие сложности. Есть же графический метод. Берете прямоугольник с 1 м и 1 м сторонами. Берете диагональ её длину и все вот он квадратный корень. Чем больше будет сторона прямоугольника тем выше будет точность. То есть можно взять прямоугольник 1 км и 1 км и померить диагональ. А так что гипотенуза является корнем знали далеко до нашей эры. Плюс не забывайте что 60тиричная система точнее в расчетах, плюс удобней, т.к. у 60-ти больше всего делителей. И мы даже перейдя на десятичную систему, так и не ушли от 360 градусов, 12 часов на циферблате и т.д.

edo1h
00.00.0000 00:00+2То есть можно взять прямоугольник 1 км и 1 км и померить диагональ
Вы правда считаете, что легко построить квадрат со стороной один километр с допусками в единицы миллиметров?

BaLord
00.00.0000 00:00-1Строили и точнее те же египетские пирамиды, проверьте для начала на 1м и 1м и увидите точность как минимум с двумя знаками, возьмете 10 на 10, будет не менее 4-6ти знаков, плюс вы мыслите в десятичном исчислении, подумайте что в 60тиричном все выглядит сильно иначе. Наиболее близкое приближение к корню из 2-х является дробь 99/70 точность ее 1 / 10000, переведите это в 60тиричное. Долгое время вавилоняне ограничивались 8-летним циклом, в котором укладывалось 99 месяцев. и число 70 в их исчислении, скорее всего тоже было достаточно простым и часто употребляемым. Мы мало знаем о тех временах, но то что по полигональной кладке блоков они опережали наше время это факт.
П.с. Удивительные факты про Вавилон.
Квадратные уравнения жители Вавилона решали еще задолго до появления на свет Христа.
-
По свидетельству Геродота, Вавилон, раскинувшийся по берегам Ефрата, имел форму огромного четырехугольника, каждая из сторон которого имела длину в 22 километра.

MegaMANGO
00.00.0000 00:00"Как вавилонянам удалось вычислить √2 с точностью до 6 знаков после запятой?" – ответ: руками. Всё, конец статьи.
Нет, серьёзно, я без особых знаний и формул могу прямо сейчас сесть с листком бумаги и ручкой, и вычислить √2 с этой же точностью ≈за пол часа. Точнее мог бы, если бы мне было нехрен делать. Я так и не понял, в чём "достижение"

edo1h
00.00.0000 00:00+2Вы можете это сделать потому что у вас есть багаж знаний, от самого понятия корня до умножения столбиком. У древних же этот багаж был совершенно другим, притом, очевидно, не столь развитым.
Понять что именно они знали и как считали на мой взгляд безумно интересно. Другое дело, что статья почти не отвечает на эти вопросы.

disputant
00.00.0000 00:00Собственно, этот результат может вызывать удивление только у тех, кто всерьез не понимает, как можно что-то посчитать без компьютера, а придумать без Гугла...
А как Архимед число "пи" находил? А это потруднее будет, чем метод "а где лежит результат? да где-то посредине" ("если x —много, то 2/x мало, так что возьмем среднее...")

Diordna
00.00.0000 00:00А мы точно первая цивилизация на этой планете? :)
А если серьёзно зачем жителям древнего Вавилона нужно было это знание какая практическая польза? Это же не календарь для земледелия например.
Gennadij_Kalin2020
00.00.0000 00:00+1они города строили, меряли участки земли, торговали так же и земельными участками.

edo1h
00.00.0000 00:00+1Так и сейчас куча областей математики или не имеет практического применения, или же применение было придумано уже потом.

masterbias
00.00.0000 00:00Мне одному кажется, что там не 24, а 23 написано? И что это за числа во второй строчке? Нет ли здесь некоторой вероятности, что это не высокая математика, а какая-нибудь меркантильная запись того, кто сколько должен автору манускрипта? :)




MAXH0
Исторический материал классный. НО изложение, если честно, заставляет желать лучшего. Читал подобный материал про число Пи, так текст воспринимался как закрученный детектив.
DirectoriX
Не удивлюсь, если оригинальный текст писался для/по мотивам видео, очень уж характерная для научпоп-каналов подача