Что такое GAN и что они могут делать?

На высоком уровне GAN — это нейронные сети, которые учатся генерировать реалистичные образцы данных, на которых они обучались. Например, имея фотографии рукописных цифр, GAN узнают, как создавать реалистичные фотографии большего количества рукописных цифр. Что еще более впечатляюще, GAN могут даже научиться создавать реалистичные фотографии людей, такие как приведенные ниже.

Так как же работают GAN? По сути, GAN изучают распределение интересующего объекта. Например. GAN, обученные рукописным цифрам, изучают распределение данных. Как только распределение данных изучено, GAN может просто выбрать из распределения для создания реалистичных изображений.

Распространение данных

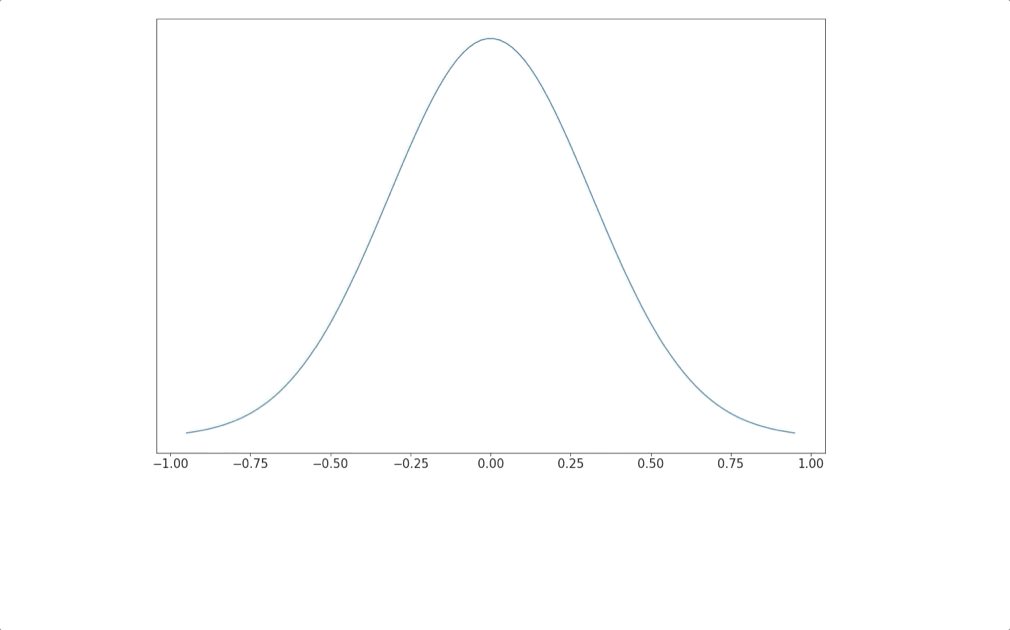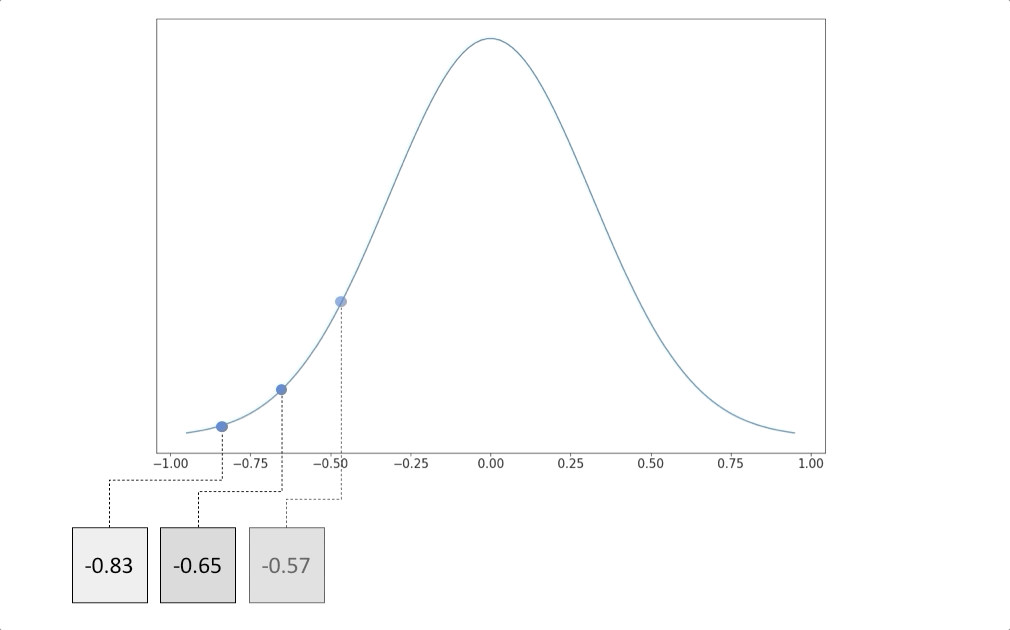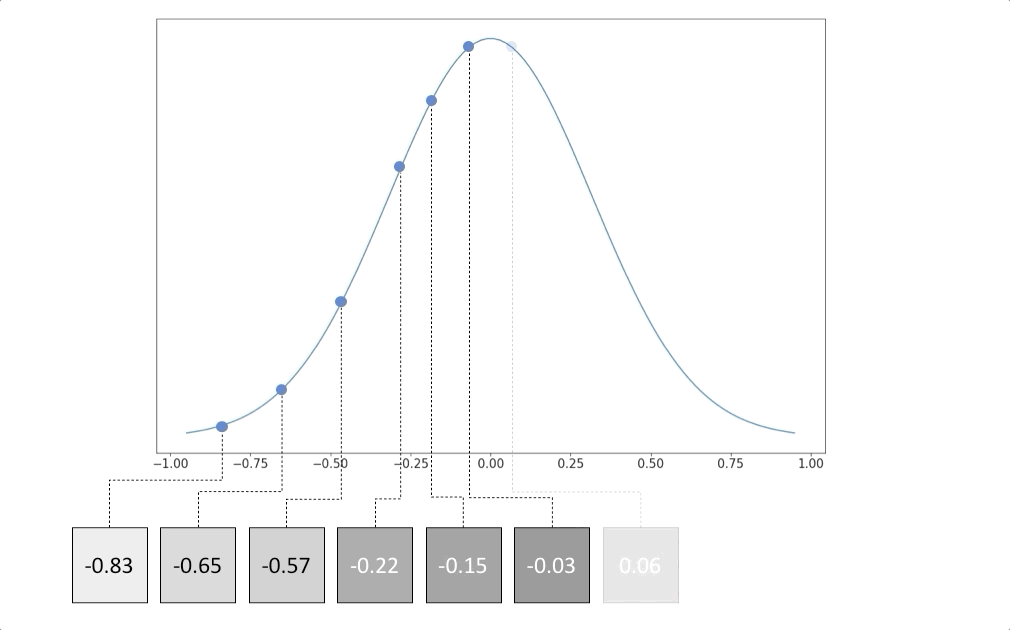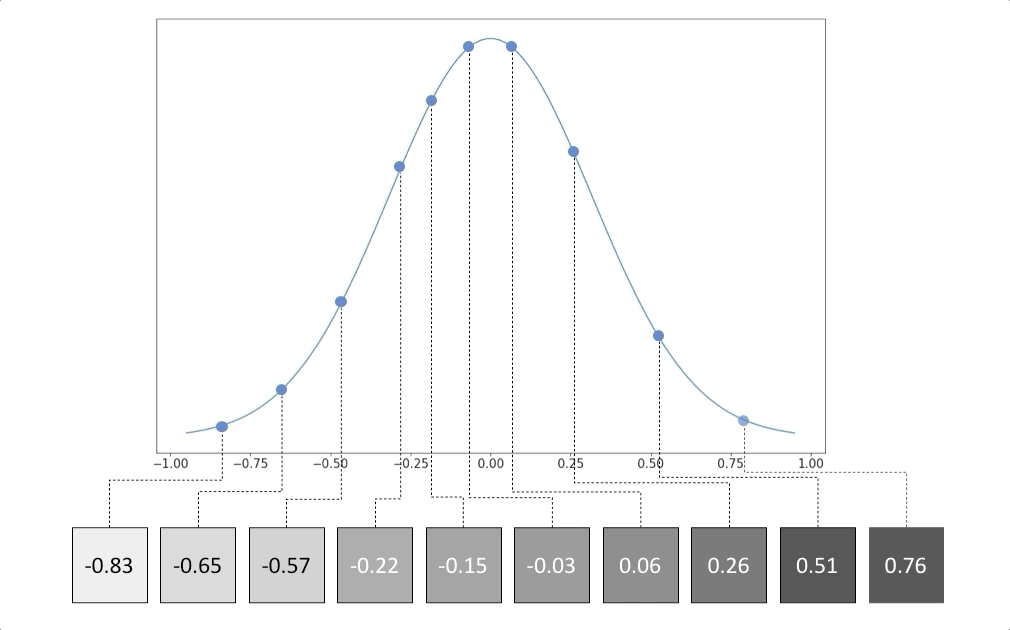
Чтобы укрепить наше понимание распределения данных, давайте рассмотрим следующий пример. Предположим, что у нас есть следующие 6 изображений ниже.

Каждое изображение представляет собой сероватый прямоугольник, и для простоты предположим, что каждое изображение состоит всего из 1 пикселя. Другими словами, в каждом изображении есть только один сероватый пиксель.

Теперь предположим, что каждый пиксель имеет возможное значение от -1 до 1, где белый пиксель имеет значение -1, а черный пиксель имеет значение 1. Таким образом, 6 серых изображений будут иметь следующие значения пикселей:

Что мы знаем о распределении значений пикселей? Что ж, просто проверив, мы знаем, что большинство значений пикселей около 0, а несколько значений приближаются к крайним значениям (-1 и 1). Поэтому мы можем предположить, что распределение является гауссовским со средним значением 0.

Примечание. При наличии большего количества выборок получить гауссово распределение этих данных тривиально, вычислив среднее значение и стандартное отклонение. Однако это не является нашей целью, поскольку рассчитать распределение данных по сложным объектам сложно, в отличие от этого простого примера.

Это распределение данных полезно, потому что оно позволяет нам генерировать больше серых изображений, как 6 выше. Чтобы создать больше похожих изображений, мы можем случайным образом выбрать из распределения.

Хотя вычисление лежащего в основе распределения серых пикселей может быть тривиальным, вычисление распределения кошек, собак, автомобилей или любого другого сложного объекта часто оказывается математически неразрешимым.

Как же тогда мы изучаем базовое распределение сложных объектов? Очевидный ответ — использовать нейронные сети. Имея достаточно данных, мы можем научить нейронную сеть изучать любую сложную функцию, например базовое распределение данных.

Генератор — модель обучения распределению

В GAN генератор — это нейронная сеть, которая изучает базовое распределение данных. Чтобы быть более конкретным, генератор принимает в качестве входных данных случайное распределение (также известное как «шум» в литературе по GAN) и изучает функцию отображения, которая отображает входные данные в желаемый результат, который является фактическим базовым распределением данных.

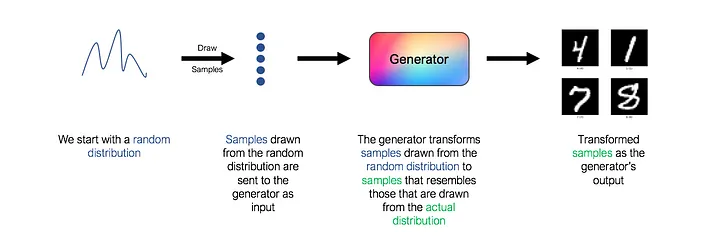
Однако обратите внимание, что в приведенной выше архитектуре отсутствует ключевой компонент. Какую функцию потерь мы должны использовать для обучения генератора? Как мы узнаем, действительно ли сгенерированные изображения напоминают настоящие рукописные цифры? Как всегда, ответ « используйте нейронную сеть ». Эта вторая сеть известна как дискриминатор.

Дискриминатор — противник Генератора

Роль дискриминатора состоит в оценке качества выходных изображений генератора. Технически дискриминатор представляет собой двоичный классификатор. Он принимает изображения в качестве входных данных и выводит вероятность того, что изображение является реальным (т. е. фактическим тренировочным изображением) или фальшивым (т. е. полученным от генератора).

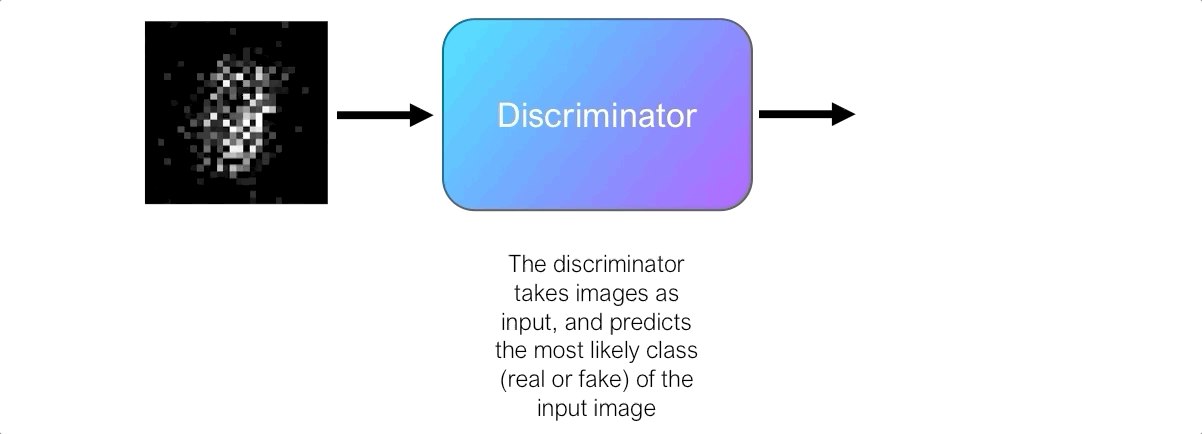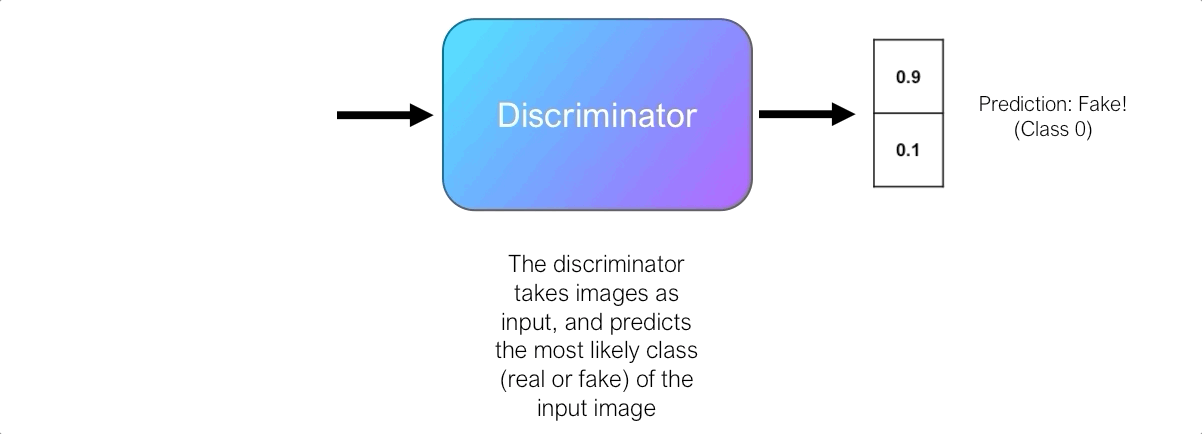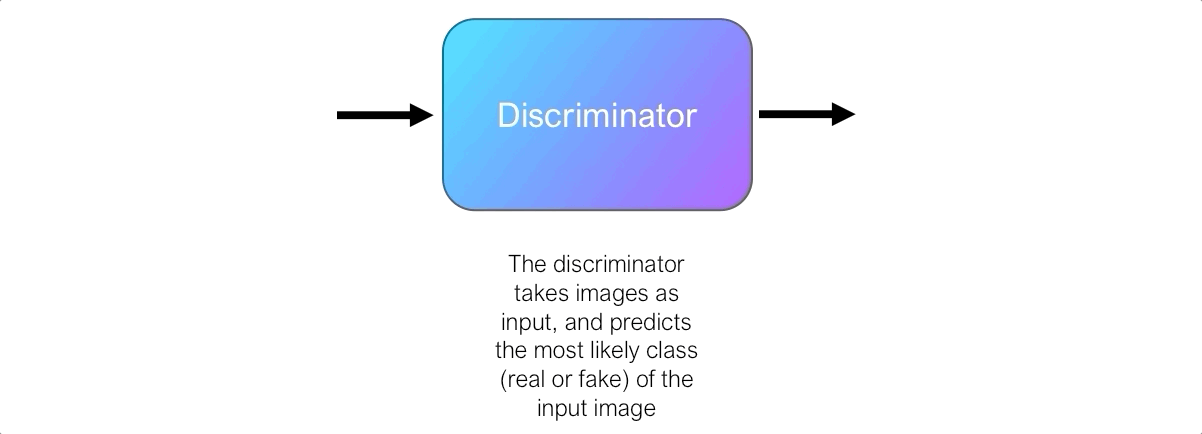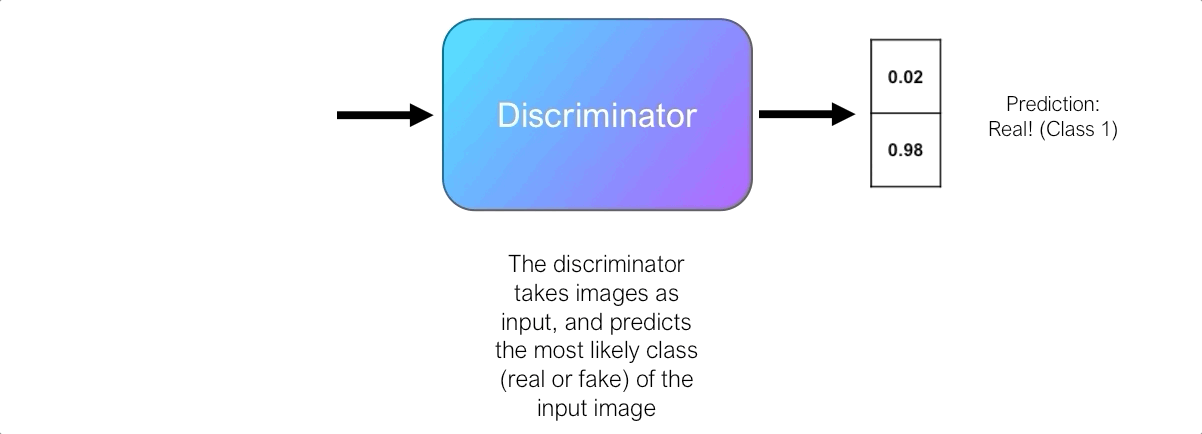
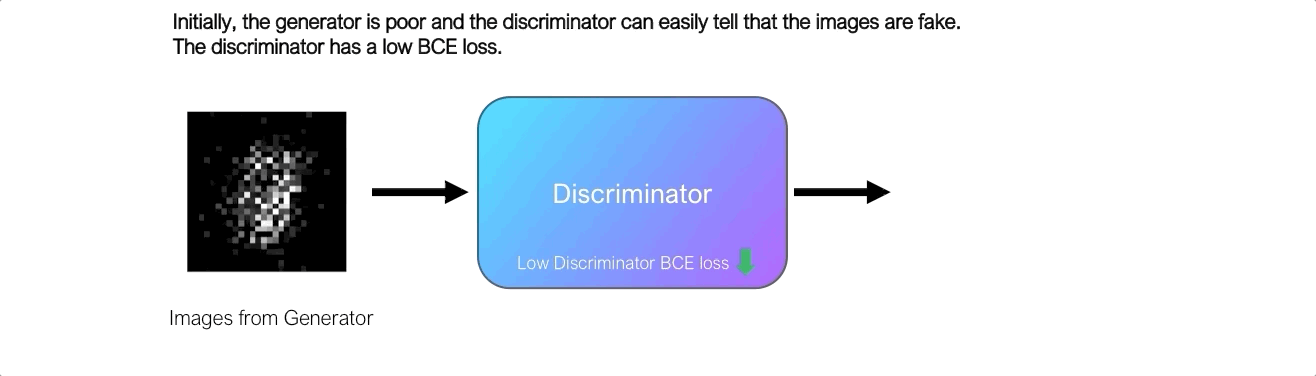
Сначала генератор изо всех сил пытается создать изображения, которые выглядят реальными, и дискриминатор может легко отличить настоящие изображения от поддельных, не делая слишком много ошибок. Поскольку дискриминатор является двоичным классификатором, мы можем количественно оценить производительность дискриминатора, используя потери двоичной кросс-энтропии .

Потери дискриминатора являются важным сигналом для генератора. Напомним ранее, что генератор сам по себе не знает, похожи ли сгенерированные изображения на реальные. Однако генератор может использовать потери BCE дискриминатора в качестве сигнала для получения обратной связи для сгенерированных им изображений.

Вот как это работает. Мы отправляем изображения, выдаваемые генератором, в дискриминатор, и он предсказывает вероятность того, что изображение реально. Первоначально, когда генератор плохой, дискриминатор может легко классифицировать изображения как поддельные, что приводит к низким потерям BCE. Однако со временем генератор улучшается, и дискриминатор начинает делать больше ошибок, ошибочно классифицируя поддельные изображения как настоящие, что приводит к более высоким потерям BCE. Следовательно, потеря BCE дискриминатора сигнализирует о качестве изображения, выводимого генератором, и генератор стремится максимизировать эту потерю.

Генератор использует потери дискриминатора как показатель качества сгенерированных им изображений. Задача генератора состоит в том, чтобы настроить свои веса таким образом, чтобы потери BCE от дискриминатора были максимальными, эффективно «обманывая» дискриминатор.

Тренировка дискриминатора

А как же дискриминатор? До сих пор мы предполагали, что у нас с самого начала есть отлично работающий дискриминатор. Однако это предположение неверно, и дискриминатор также требует обучения.

Поскольку дискриминатор является бинарным классификатором, процедура его обучения проста. Мы предоставим дискриминатору набор помеченных реальных и поддельных изображений и будем использовать потери BCE для настройки весов дискриминатора. Мы обучаем дискриминатор распознавать настоящие и поддельные изображения, предотвращая «обман» дискриминатора генератором.

GAN — история о двух сетях

Давайте теперь соберем все вместе и посмотрим, как работают GAN.

К настоящему времени вы знаете, что GAN состоят из двух взаимосвязанных сетей, генератора и дискриминатора. В обычных GAN генераторы и дискриминаторы представляют собой простые нейронные сети с прямой связью.

Что уникально для GAN, так это то, что генератор и дискриминатор обучаются по очереди, враждебно друг другу.

Для обучения генератора мы используем в качестве входных данных вектор шума, выбранный из случайного распределения. На практике мы используем вектор длины 100, взятый из гауссовского распределения, в качестве вектора шума. Входные данные проходят через ряд полностью связанных слоев в нейронной сети с прямой связью. Выход генератора — это изображение, которое в нашем примере MNIST представляет собой 28x28массив. Генератор передает свой вывод дискриминатору и использует потери BCE дискриминатора для настройки своих весов с целью максимизации потерь дискриминатора.

Для обучения дискриминатора мы используем помеченные изображения из генератора, а также реальные изображения в качестве входных данных. Дискриминатор учится классифицировать изображения как настоящие или поддельные и обучается с помощью функции потерь BCE.

На практике мы обучаем генератор и дискриминатор по очереди, один за другим. Эта схема обучения похожа на минимаксную состязательную игру для двух игроков, поскольку генератор стремится максимизировать потери дискриминатора, а дискриминатор стремится минимизировать свои собственные потери.

Создание собственной ГАН

Теперь, когда мы понимаем теорию, лежащую в основе GAN, давайте применим ее на практике, создав собственную GAN с нуля с помощью PyTorch!

Прежде всего, давайте добавим набор данных MNIST. Библиотека torchvisionпозволяет нам легко получить набор данных MNIST. Мы выполним некоторую стандартную нормализацию изображений перед сведением 28x28изображений MNIST к 784тензору. Это выравнивание необходимо, поскольку слои в сети являются полностью связанными слоями.

import torch
import torch.nn as nn
from torch.utils.data import DataLoader
from torchvision import transforms, datasets

mnist_transforms = transforms.Compose([transforms.ToTensor(),
                                       transforms.Normalize(mean=0.5, std=0.5),
                                       transforms.Lambda(lambda x: x.view(-1, 784))])

data = datasets.MNIST(root='/data/MNIST', download=True, transform=mnist_transforms)

mnist_dataloader = DataLoader(data, batch_size=128, shuffle=True, num_workers=4) 

Далее давайте напишем код для класса генератора. Из того, что мы видели ранее, генератор — это просто нейронная сеть с прямой связью, которая принимает 100тензор длины и выдает 784тензор. В генераторе размер плотных слоев обычно удваивается после каждого слоя (256, 512, 1024).

class Generator(nn.Module):
  '''
  Generator class. Accepts a tensor of size 100 as input as outputs another
  tensor of size 784. Objective is to generate an output tensor that is
  indistinguishable from the real MNIST digits 
  '''
  
  def __init__(self):
    super().__init__()
    self.layer1 = nn.Sequential(nn.Linear(in_features=100, out_features=256),
                                nn.LeakyReLU())
    self.layer2 = nn.Sequential(nn.Linear(in_features=256, out_features=512),
                                nn.LeakyReLU())
    self.layer3 = nn.Sequential(nn.Linear(in_features=512, out_features=1024),
                                nn.LeakyReLU())
    self.output = nn.Sequential(nn.Linear(in_features=1024, out_features=28*28),
                                nn.Tanh())

  def forward(self, x):
    x = self.layer1(x)
    x = self.layer2(x)
    x = self.layer3(x)
    x = self.output(x)
    return x

Это было легко, не так ли? Теперь давайте напишем код для класса дискриминатора. Дискриминатор также представляет собой нейронную сеть с прямой связью, которая принимает 784тензор длины и выдает тензор размера 1, обозначающий вероятность того, что входные данные принадлежат классу 1 (реальное изображение). В отличие от генератора, мы уменьшаем вдвое размер плотных слоев после каждого слоя (1024, 512, 256).

class Discriminator(nn.Module):
  '''
  Discriminator class. Accepts a tensor of size 784 as input and outputs
  a tensor of size 1 as  the predicted class probabilities
  (generated or real data)
  '''

  def __init__(self):
    super().__init__()
    self.layer1 = nn.Sequential(nn.Linear(in_features=28*28, out_features=1024),
                                nn.LeakyReLU())
    self.layer2 = nn.Sequential(nn.Linear(in_features=1024, out_features=512),
                                nn.LeakyReLU())
    self.layer3 = nn.Sequential(nn.Linear(in_features=512, out_features=256),
                                nn.LeakyReLU())
    self.output = nn.Sequential(nn.Linear(in_features=256, out_features=1),
                                nn.Sigmoid())
    
  def forward(self, x):
    x = self.layer1(x)
    x = self.layer2(x)
    x = self.layer3(x)
    x = self.output(x)
    return x

Теперь мы собираемся создать класс GAN, который включает в себя как класс генератора, так и класс дискриминатора. Этот класс GAN будет содержать код для обучения генератора и дискриминатора по очереди, в соответствии со схемой обучения, которую мы обсуждали ранее. Мы собираемся использовать для этого PyTorch Lightning , чтобы упростить наш код и сократить шаблонный код.

import pytorch_lightning as pl

class GAN(pl.LightningModule):

  def __init__(self):
    super().__init__()
    self.generator = Generator()
    self.discriminator = Discriminator()
    # After each epoch, we generate 100 images using the noise
    # vector here (self.test_noises). We save the output images
    # in a list (self.test_progression) for plotting later.
    self.test_noises = torch.randn(100,1,100, device=device)
    self.test_progression = []

  def forward(self, z):
    """
    Generates an image using the generator
    given input noise z
    """
    return self.generator(z)

  def generator_step(self, x):
    """
    Training step for generator
    1. Sample random noise
    2. Pass noise to generator to
       generate images
    3. Classify generated images using
       the discriminator
    4. Backprop loss to the generator
    """
    
    # Sample noise
    z = torch.randn(x.shape[0], 1, 100, device=device)

    # Generate images
    generated_imgs = self(z)

    # Classify generated images
    # using the discriminator
    d_output = torch.squeeze(self.discriminator(generated_imgs))

    # Backprop loss. We want to maximize the discriminator's
    # loss, which is equivalent to minimizing the loss with the true
    # labels flipped (i.e. y_true=1 for fake images). We do this
    # as PyTorch can only minimize a function instead of maximizing
    g_loss = nn.BCELoss()(d_output,
                           torch.ones(x.shape[0], device=device))

    return g_loss

  def discriminator_step(self, x):
    """
    Training step for discriminator
    1. Get actual images
    2. Predict probabilities of actual images and get BCE loss
    3. Get fake images from generator
    4. Predict probabilities of fake images and get BCE loss
    5. Combine loss from both and backprop loss to discriminator
    """
    
    # Real images
    d_output = torch.squeeze(self.discriminator(x))
    loss_real = nn.BCELoss()(d_output,
                             torch.ones(x.shape[0], device=device))

    # Fake images
    z = torch.randn(x.shape[0], 1, 100, device=device)
    generated_imgs = self(z)
    d_output = torch.squeeze(self.discriminator(generated_imgs))
    loss_fake = nn.BCELoss()(d_output,
                             torch.zeros(x.shape[0], device=device))

    return loss_real + loss_fake

  def training_step(self, batch, batch_idx, optimizer_idx):
    X, _ = batch

    # train generator
    if optimizer_idx == 0:
      loss = self.generator_step(X)
    
    # train discriminator
    if optimizer_idx == 1:
      loss = self.discriminator_step(X)

    return loss

  def configure_optimizers(self):
    g_optimizer = torch.optim.Adam(self.generator.parameters(), lr=0.0002)
    d_optimizer = torch.optim.Adam(self.discriminator.parameters(), lr=0.0002)
    return [g_optimizer, d_optimizer], []

  def training_epoch_end(self, training_step_outputs):
    epoch_test_images = self(self.test_noises)
    self.test_progression.append(epoch_test_images)

Теперь мы можем обучить наш GAN. Мы будем обучать его с помощью графического процессора в течение 100 эпох.

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

model = GAN()

trainer = pl.Trainer(max_epochs=100, gpus=1)
trainer.fit(model, mnist_dataloader)

Визуализация сгенерированных изображений

Осталось только визуализировать сгенерированные изображения. В training_epoch_end()функции из нашего класса GAN выше мы сохраняли изображения, выводимые генератором после каждой эпохи обучения, в список.

Мы можем визуализировать эти изображения, нанеся их на сетку. Приведенный ниже код случайным образом выбирает 10 изображений, сгенерированных после 100-й эпохи обучения, и наносит их на сетку.

import numpy as np
from matplotlib import pyplot as plt, gridspec

# Convert images from torch tensor to numpy array
images = [i.detach().cpu().numpy() for i in model.test_progression]

epoch_to_plot = 100
nrow = 3
ncol = 8

# randomly select 10 images for plotting
indexes = np.random.choice(range(100), nrow*ncol, replace=False)

fig = plt.figure(figsize=((ncol+1)*2, (nrow+1)*2)) 
fig.suptitle('Epoch {}'.format(epoch_to_plot), fontsize=30)

gs = gridspec.GridSpec(nrow, ncol,
         wspace=0.0, hspace=0.0, 
         top=1.-0.5/(nrow+1), bottom=0.5/(nrow+1), 
         left=0.5/(ncol+1), right=1-0.5/(ncol+1)) 

for i in range(nrow):
    for j in range(ncol):
        idx = i*ncol + j
        img = np.reshape(images[epoch_to_plot-1][indexes[idx]], (28,28))
        ax = plt.subplot(gs[i,j])
        ax.imshow(img, cmap='gray')
        ax.axis('off')

Наконец, как и было обещано, мы создадим анимацию, показанную вверху поста. Используя FuncAnimationфункцию в matplotlib, мы будем анимировать изображения на графике кадр за кадром.

import numpy as np
from matplotlib import pyplot as plt, gridspec, rc
from matplotlib.animation import FuncAnimation
rc('animation', html='jshtml')

images = [i.detach().cpu().numpy() for i in model.test_progression]

nrow = 3
ncol = 8

indexes = np.random.choice(range(100), nrow*ncol, replace=False)

fig = plt.figure(figsize=((ncol+1)*2, (nrow+1)*2)) 

gs = gridspec.GridSpec(nrow, ncol,
         wspace=0.0, hspace=0.0, 
         top=1.-0.5/(nrow+1), bottom=0.5/(nrow+1), 
         left=0.5/(ncol+1), right=1-0.5/(ncol+1)) 

for i in range(nrow):
  for j in range(ncol):
    ax = plt.subplot(gs[i,j])
    ax.axis('off')

def animate(frame):
  fig.suptitle('Epoch {}'.format(frame), fontsize=30)
  ret = []
  for i in range(nrow):
    for j in range(ncol):
      idx = i*ncol + j
      img = np.reshape(images[frame][indexes[idx]], (28,28))
      ax = fig.axes[idx]
      ax.imshow(img, cmap='gray')
      ret.append(ax.get_images()[0])
  return ret
    
anim = FuncAnimation(fig, animate, frames=100, interval=50, blit=True)

Что дальше?

Поздравляю! Вы дошли до конца этого урока. Надеюсь, вам понравилось читать это так же, как мне понравилось писать это.