Что такое переоснащение/недообучение модели?

Как уже упоминалось, в статистике и машинном обучении мы обычно разделяем наши данные на два подмножества: данные обучения и данные тестирования (а иногда и на три: обучение, проверка и тестирование) и подгоняем нашу модель к данным обучения, чтобы делать прогнозы. тестовые данные. Когда мы это делаем, может произойти одно из двух: мы переобходим нашу модель или не подберем ее. Мы не хотим, чтобы что-либо из этого происходило, потому что они влияют на предсказуемость нашей модели — мы можем использовать модель с меньшей точностью и/или необобщенную (это означает, что вы не можете обобщать свои прогнозы на других данных). Давайте посмотрим, что на самом деле означают подгонка и переоснащение.

Переоснащение

Переобучение означает, что модель, которую мы обучили, обучилась «слишком хорошо» и теперь слишком близко подходит к обучающему набору данных. Обычно это происходит, когда модель слишком сложна (т. е. слишком много признаков/переменных по сравнению с количеством наблюдений). Эта модель будет очень точной на обучающих данных, но, вероятно, будет очень неточной на необученных или новых данных. Это потому, что эта модель не является обобщенной (или не является обобщенной), что означает, что вы можете обобщать результаты и не можете делать какие-либо выводы на основе других данных, что, в конечном счете, вы и пытаетесь сделать. По сути, когда это происходит, модель изучает или описывает «шум» в обучающих данных, а не фактические отношения между переменными в данных. Этот шум, очевидно, не является частью какого-либо нового набора данных и не может быть применен к нему.

Недооснащение

В отличие от переобучения, когда модель недообучена, это означает, что модель не соответствует обучающим данным и, следовательно, пропускает тенденции в данных. Это также означает, что модель нельзя обобщить на новые данные. Как вы, наверное, догадались (или поняли!), обычно это результат очень простой модели (недостаточно предикторов/независимых переменных). Это также может произойти, когда, например, мы подгоняем линейную модель к данным, которые не являются линейными. Само собой разумеется, что эта модель будет иметь плохую прогностическую способность (на обучающих данных и не может быть обобщена на другие данные).

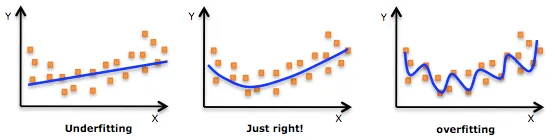
Стоит отметить, что недообучение не так распространено, как переоснащение. Тем не менее, мы хотим избежать обеих этих проблем при анализе данных. Можно сказать, что мы пытаемся найти золотую середину между недообучением и переоснащением нашей модели. Как вы увидите, разделение обучения/тестирования и перекрестная проверка помогают избежать переобучения, а не недообучения. Давайте погрузимся в них обоих!

Обучение/тестовый

Как я уже говорил, данные, которые мы используем, обычно делятся на обучающие и тестовые данные. Обучающий набор содержит известные выходные данные, и модель учится на этих данных, чтобы позже обобщить их на другие данные. У нас есть тестовый набор данных (или подмножество), чтобы проверить прогноз нашей модели на этом подмножестве.

Давайте посмотрим, как это сделать в Python. Мы сделаем это с помощью библиотеки Scikit-Learn и, в частности, метода train_test_split . Начнем с импорта необходимых библиотек:

import pandas as pd
from sklearn import datasets, linear_model
from sklearn.model_selection import train_test_split
from matplotlib import pyplot as plt

• Давайте быстро пробежимся по библиотекам, которые я импортировал:

  • Pandas — загрузить файл данных в виде фрейма данных Pandas и проанализировать данные.

  • Из Sklearn я импортировал модуль наборов данных , чтобы загрузить образец набора данных, и linear_model , чтобы запустить линейную регрессию.

  • Из Sklearn, подбиблиотеки model_selection , я импортировал train_test_split , так что я могу разделить наборы для обучения и тестирования.

  • Из Matplotlib я импортировал pyplot для построения графиков данных.

ОК, все готово! Давайте загрузим набор данных о диабете , превратим его в фрейм данных и определим имена столбцов:

# Load the Diabetes dataset
columns = “age sex bmi map tc ldl hdl tch ltg glu”.split() # Declare the columns names
diabetes = datasets.load_diabetes() # Call the diabetes dataset from sklearn
df = pd.DataFrame(diabetes.data, columns=columns) # load the dataset as a pandas data frame
y = diabetes.target # define the target variable (dependent variable) as y

Теперь мы можем использовать функцию train_test_split для разделения. test_size =0.2 внутри функции указывает процент данных, которые должны быть сохранены для тестирования. Обычно это 80/20 или 70/30.

# create training and testing vars
X_train, X_test, y_train, y_test = train_test_split(df, y, test_size=0.2)
print X_train.shape, y_train.shape
print X_test.shape, y_test.shape
(353, 10) (353,)
(89, 10) (89,)

Теперь подгоним модель к обучающим данным:

# fit a model
lm = linear_model.LinearRegression()
model = lm.fit(X_train, y_train)
predictions = lm.predict(X_test)

Как видите, мы подгоняем модель к обучающим данным и пытаемся предсказать тестовые данные. Давайте посмотрим, каковы (некоторые) прогнозы:

predictions[0:5]
array([ 205.68012533,   64.58785513,  175.12880278,  169.95993301,
        128.92035866])

Примечание: поскольку я использовал [0:5] после прогнозов, он показал только первые пять прогнозируемых значений. Удаление [0:5] заставило бы его напечатать все предсказанные значения, созданные нашей моделью.

Построим модель:

## The line / model
plt.scatter(y_test, predictions)
plt.xlabel(“True Values”)
plt.ylabel(“Predictions”)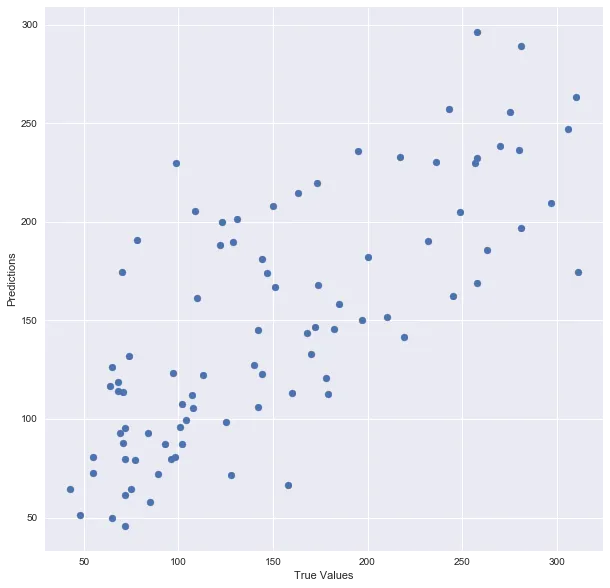

And print the accuracy score:

print “Score:”, model.score(X_test, y_test)
Score: 0.485829586737

Ну вот! Вот краткое изложение того, что я сделал: я загрузил данные, разделил их на наборы для обучения и тестирования, подогнал модель регрессии к данным обучения, сделал прогнозы на основе этих данных и проверил прогнозы на тестовых данных. Кажется хорошим, верно?Но разделение обучения/тестирования имеет свои опасности — что, если разделение, которое мы делаем, не является случайным? Что, если в одном подмножестве наших данных есть только люди из определенного штата, сотрудники с определенным уровнем дохода, но не с другим уровнем дохода, только женщины или только люди определенного возраста? (представьте себе файл, заказанный одним из них). Это приведет к переоснащению, хотя мы пытаемся этого избежать! Вот где вступает в действие перекрестная проверка.

Перекрестная проверка

В предыдущем абзаце я упомянул о предостережениях в методе разделения обучения/тестирования. Чтобы избежать этого, мы можем выполнить нечто, называемое перекрестной проверкой . Это очень похоже на разделение обучения/тестирования, но применяется к большему количеству подмножеств. Это означает, что мы разделяем наши данные на k подмножеств и обучаем на k-1 одно из этих подмножеств. Что мы делаем, так это сохраняем последнее подмножество для проверки. Мы можем сделать это для каждого из подмножеств.

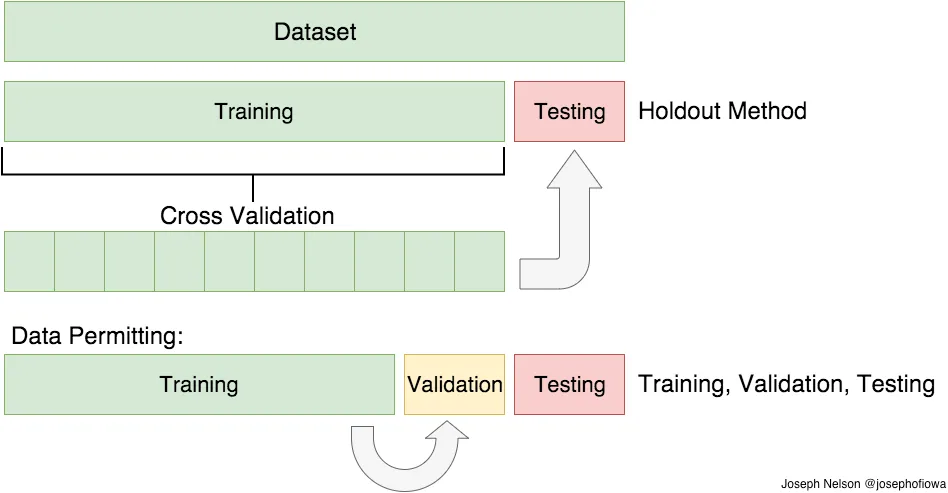
Существует множество методов перекрестной проверки, я рассмотрю два из них: первый — перекрестная проверка K-Folds , а второй — перекрестная проверка с исключением одного (LOOCV).

K-кратная перекрестная проверка

В K-Folds Cross Validation мы разделяем наши данные на k различных подмножеств (или складок). Мы используем подмножества k-1 для обучения наших данных и оставляем последнее подмножество (или последнюю складку) в качестве тестовых данных. Затем мы усредняем модель по каждой из складок, а затем завершаем нашу модель. После этого мы тестируем его на тестовом наборе.

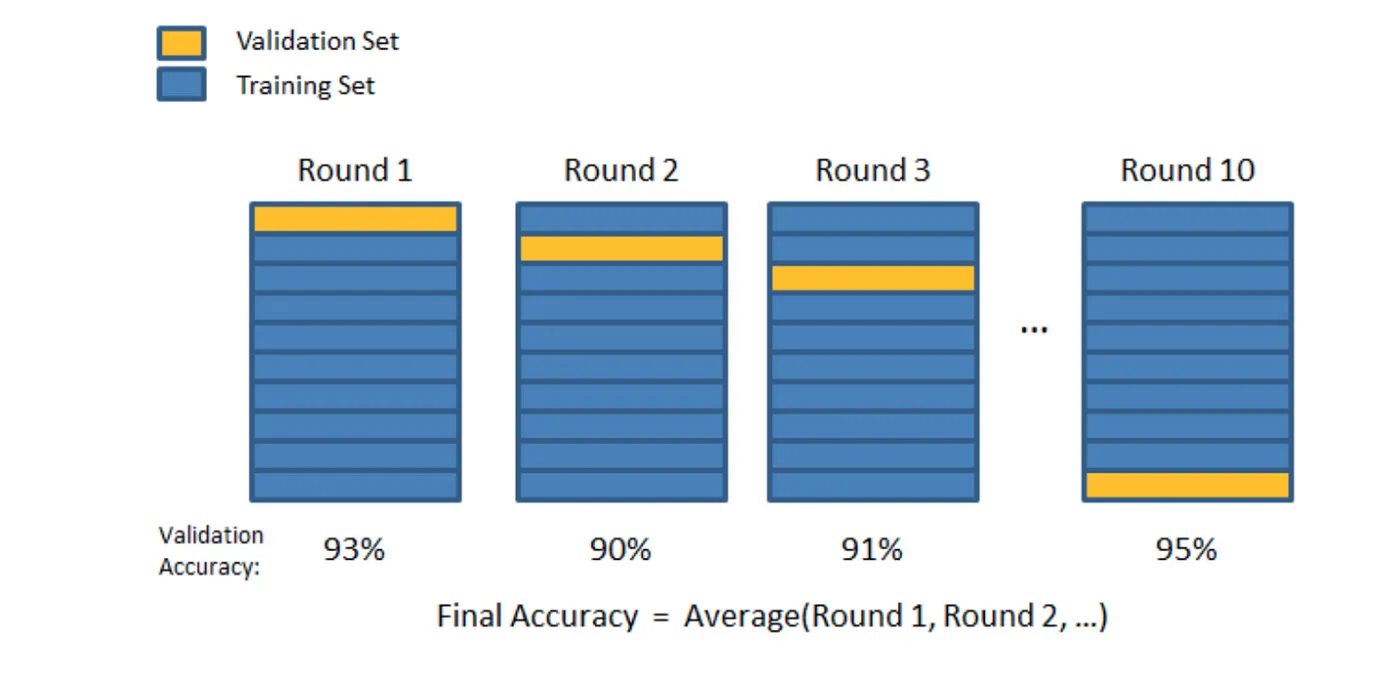
Вот очень простой пример из документации Sklearn для K-Folds:

from sklearn.model_selection import KFold # import KFold
X = np.array([[1, 2], [3, 4], [1, 2], [3, 4]]) # create an array
y = np.array([1, 2, 3, 4]) # Create another array
kf = KFold(n_splits=2) # Define the split - into 2 folds 
kf.get_n_splits(X) # returns the number of splitting iterations in the cross-validator
print(kf) 
KFold(n_splits=2, random_state=None, shuffle=False)

И посмотрим на результат:

for train_index, test_index in kf.split(X):
 print(“TRAIN:”, train_index, “TEST:”, test_index)
 X_train, X_test = X[train_index], X[test_index]
 y_train, y_test = y[train_index], y[test_index]
('TRAIN:', array([2, 3]), 'TEST:', array([0, 1]))
('TRAIN:', array([0, 1]), 'TEST:', array([2, 3]))

Как видите, функция разделила исходные данные на разные подмножества данных. Опять же, очень простой пример, но я думаю, что он довольно хорошо объясняет концепцию.

Это еще один метод перекрестной проверки, Leave One Out Cross Validation (кстати, эти методы не единственные два, есть куча других методов перекрестной проверки. Ознакомьтесь с ними на сайте Sklearn ) . В этом типе перекрестной проверки количество складок (подмножеств) равно количеству наблюдений, которые у нас есть в наборе данных. Затем мы усредняем ВСЕ эти складки и строим нашу модель со средним значением. Затем мы тестируем модель относительно последней складки. Поскольку мы получили бы большое количество обучающих наборов (равное количеству выборок), этот метод требует больших вычислительных затрат и должен использоваться на небольших наборах данных. Если набор данных большой, скорее всего, будет лучше использовать другой метод, например, kfold.

Давайте посмотрим на другой пример от Sklearn:

from sklearn.model_selection import LeaveOneOut 
X = np.array([[1, 2], [3, 4]])
y = np.array([1, 2])
loo = LeaveOneOut()
loo.get_n_splits(X)


for train_index, test_index in loo.split(X):
   print("TRAIN:", train_index, "TEST:", test_index)
   X_train, X_test = X[train_index], X[test_index]
   y_train, y_test = y[train_index], y[test_index]
   print(X_train, X_test, y_train, y_test)

И посмотрим на результат:

('TRAIN:', array([1]), 'TEST:', array([0]))
(array([[3, 4]]), array([[1, 2]]), array([2]), array([1]))
('TRAIN:', array([0]), 'TEST:', array([1]))
(array([[1, 2]]), array([[3, 4]]), array([1]), array([2]))

Опять же, простой пример, но я действительно думаю, что он помогает понять основную концепцию этого метода.

Итак, какой метод мы должны использовать? Сколько складок? Что ж, чем больше у нас будет складок, мы будем уменьшать ошибку из-за смещения, но увеличивать ошибку из-за дисперсии; стоимость вычислений, очевидно, также возрастет — чем больше у вас будет сверток, тем больше времени потребуется для их вычисления и вам потребуется больше памяти. При меньшем количестве кратностей мы уменьшаем ошибку из-за дисперсии, но ошибка из-за смещения будет больше. Это также будет дешевле в вычислительном отношении. Поэтому в больших наборах данных обычно рекомендуется k=3. В небольших наборах данных, как я упоминал ранее, лучше всего использовать LOOCV.

Давайте проверим пример, который я использовал ранее, на этот раз с использованием перекрестной проверки. Я буду использовать функцию cross_val_predict , чтобы возвращать предсказанные значения для каждой точки данных, когда она находится в тестовом срезе.

# Necessary imports: 
from sklearn.model_selection import cross_val_score, cross_val_predict
from sklearn import metrics

Как вы помните, ранее я создал разделение обучения/тестирования для набора данных по диабету и подогнал модель. Давайте посмотрим, какова оценка после перекрестной проверки:

# Perform 6-fold cross validation
scores = cross_val_score(model, df, y, cv=6)
print “Cross-validated scores:”, scores
Cross-validated scores: [ 0.4554861   0.46138572  0.40094084  0.55220736  0.43942775  0.56923406]

Как видите, последняя кратность улучшила показатель исходной модели — с 0,485 до 0,569. Не ошеломительный результат, но эй, мы возьмем то, что мы можем получить :)

Теперь давайте построим новые прогнозы после выполнения перекрестной проверки:

# Make cross validated predictions
predictions = cross_val_predict(model, df, y, cv=6)
plt.scatter(y, predictions)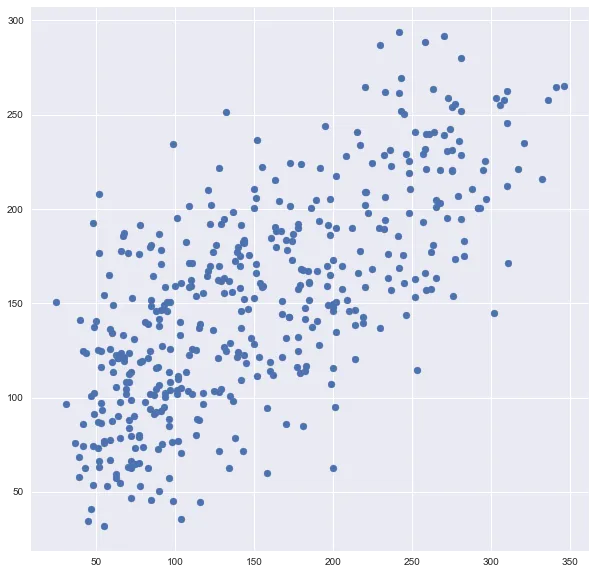

Вы можете видеть, что это сильно отличается от оригинального сюжета. Это в шесть раз больше точек, чем исходный график, потому что я использовал cv=6.

Наконец, давайте проверим оценку R² модели (R² — это «число, указывающее долю дисперсии в зависимой переменной, которая предсказуема на основе независимой переменной (переменных)». По сути, насколько точна наша модель):

accuracy = metrics.r2_score(y, predictions)
print “Cross-Predicted Accuracy:”, accuracy
Cross-Predicted Accuracy: 0.490806583864

Вот и все на этот раз! Надеюсь, вам понравился этот пост.