Привет! Меня зовут Ирина Кротова, я NLP-исследователь из компании MTS AI. В этой статье из цикла про разметку данных я расскажу об ещё одном способе собирать данные более качественно и экономить на разметке — фильтрации похожих друг на друга текстов.

В предыдущей статье я рассказывала о том, что такое аннотация данных, как это связано с работой инженера машинного обучения и о способах сократить количество ручной разметки в проекте.

Точные совпадения

Идея удалить полные дубликаты перед разметкой кажется очевидной: предполагается, что мы уже имеем дело с отфильтрованным чистым датасетом. На практике почти на каждом этапе у нас есть шанс получить дублирующиеся тексты. Причины могут быть разнообразными, начиная от спам-сообщений пользователей и заканчивая багом в коде.

Если ресурсов на разметку данных мало, то будет особенно неприятно случайно разметить одни и те же примеры.

Даже если есть полная уверенность в том, что никаких дубликатов не должно было остаться, вызов drop_duplicates в pandas занимает меньше минуты, но может легко сэкономить часы работы аннотаторов.

Неточные совпадения

Кроме полного совпадения, часто встречаются неполные дубликаты — тексты с почти одним и тем же содержанием.

Например, почти одинаковые страницы в поисковой выдаче, разнообразный плагиат, зеркала одного и того же вебсайта и копирование контента новостными агрегаторами.

На уровне коротких текстов подобные проблемы возникают в user-generated контенте и том, что им притворяется: одна площадка для сбора отзывов копирует отзывы с другой, недовольный продуктом пользователь оставил похожие сообщения несколько раз на каждом сайте или, как в примере ниже, спамеры шлют сообщения в игровой чат.

Такие тексты тоже стоило бы удалять из выборки, но часто между ними нет полного совпадения: есть лишние слова или абзацы, пропуски, в конце потерян знак препинания.

Сразу отмечу, что дальше под дубликатами я буду иметь в виду именно сообщения, которые отличаются друг от друга на уровне неудачного копипастинга текстов, но не на уровне смысла (например, перефразирование). В каких-то случаях может быть полезно удалить ещё и тексты, близкие по смыслу — всё зависит от постановки задачи. Но для классических задач вроде классификации интентов или определения тональности отзывов разные способы выразить одну и ту же мысль обычно как раз интересны ("Телефон просто супер!", "Отличный телефон", "Телефон очень понравился"), а вот из отзывов "Телефон прсто супер!!!" и "Телефон просто супер" может быть полезно оставить только один.

Как найти такие дубликаты?

Мера близости Жаккара

Если датасет не очень большой, то можно построить попарную матрицу расстояний между всеми текстами. Один из самых простых способов посчитать такие расстояния — мера близости Жаккара.

Идея в том, чтобы представить оба текста в виде множества n-грамм (посимвольно или пословно) и найти соотношение между пересечением n-грамм и всеми n-граммами обоих текстов.

Попробуем посчитать такие расстояния для текстов из чата с картинки выше.

message = "Selling cheap coins. 1K=5.9$"

# текст с теми же словами, но в другом порядке: 
permuted_message = "1K=5.9$ Selling cheap coins."
# текст с частичным совпадением:
similar_message = "Selling cheap coins. good stock. Price 1000 coins =$5.9"
# полностью отличающийся текст:
different_message = "food is out of combat"

Разбиваем текст самым простым способом — по пробелам, выводим на экран множество всех оригинальных токенов:

message = set(message.split())
permuted_message = set(permuted_message.split())
similar_message = set(similar_message.split())
different_message = set(different_message.split())

print(message)
# {'cheap', '1K=5.9$', 'Selling', 'coins.'}

print(permuted_message)
# {'cheap', '1K=5.9$', 'Selling', 'coins.'}

print(similar_message)
# {'=$5.9', 'Selling', 'good', 'Price', 'coins', \
#'coins.','1000', 'stoc.', 'cheap'}

print(different_message)
# {'out', 'combat', 'of', 'food', 'is'}

Вычисляем индекс Жаккара между текстами:

def jaccard(x: set, y: set):
    shared = x.intersection(y)  # выбираем пересекающиеся токены
    return len(shared) / len(x.union(y))

# Для идентичных сообщений:
print(jaccard(message, message))
# 1.0

# Для того же текста с другим порядком слов:
print(jaccard(message, permuted_message))
# 1.0

# Для частично дублирующихся сообщений:
print(jaccard(message, similar_message))
# 0.3

# Для полностью разных текстов:
print(jaccard(message, different_message))
# 0.0

Способ поиска близких текстов максимально простой: нет почти никакого предпроцессинга текста (удаление пунктуации или стоп-слов), никак не учитывается схожесть элементов 1K=5.9$ и =$5.9 и порядок слов в тексте. Тем не менее, даже такой достаточно примитивный подход может быть хорошим бейзлайном, и часто его будет достаточно.

Как этот подход улучшить?

Shingling

Качественно улучшить поиск дубликатов можно с помощью шинглов (w-shingling), также известных как n-граммы. Идея в том, чтобы представить текст как последовательности из n идущих подряд в тексте элементов, посимвольно или пословно.

Например, посимвольными би-граммами для строки Удаление дубликатов будут ['Уд', 'да', 'ал', 'ле', 'ен', 'ни', 'ие', 'е ', ' д', 'ду', 'уб', 'бл', 'ли', 'ик', 'ка', 'ат', 'то', 'ов'].

Попробуем такой подход для три-грамм:

def text_to_ngrams(text, N=3):
    return [text[i:i+N] for i in range(len(text)-N+1)]

print(text_to_ngrams(message))
# ['Sel', 'ell', 'lli', 'lin', 'ing', 'ng ', \
# 'g c', ' ch', 'che', 'hea', 'eap', 'ap ', 'p c', \
# ' co', 'coi', 'oin', 'ins', 'ns.', 's. ', '. 1', \
# ' 1K', '1K=', 'K=5', '=5.', '5.9', '.9$']

message = set(text_to_ngrams(message))
permuted_message = set(text_to_ngrams(permuted_message))
similar_message = set(text_to_ngrams(similar_message))
different_message = set(text_to_ngrams(different_message))

# Для идентичных сообщений:
print(jaccard(message, message))
# 1.0

# Для того же текста с другим порядком слов:
print(jaccard(message, permuted_message))
# 0.7931034482758621

# Для частично дублирующихся сообщений:
print(jaccard(message, similar_message))
# 0.37037037037037035

# Для полностью разных текстов:
print(jaccard(message, different_message))
# 0.022727272727272728

По сравнению с предыдущим подходом метод с n-граммами явно более чувствителен к перестановке слов в тексте и опечаткам.

Как понять, какие параметры для разбиения текста на n-граммы лучше выбрать для вашего датасета?

Мой опыт и "общее знание" подсказывают, что если вы имеете дело с небольшими сообщениями (реплики в чатах, твиты), то хорошо работают посимвольные n-граммы с N от трёх до пяти. С большими текстами (поиск дубликатов между статьями, веб-страницами) можно брать пословные n-граммы с N от семи до десяти.

В классической книге Mining of Massive Datasets это число убедительно обосновывается таким способом:

• представим, что мы работаем с электронными письмами на английском языке, состоящими только из букв (26 в английском алфавите) и пробелов;

• в таком случае мы получим возможных шинглов (n-грамм);

• поскольку типичное письмо меньше, чем 14 миллионов символов, мы предполагаем, что будет работать достаточно хорошо.

Но в любом случае нужно смотреть на данные и задачу.

Например, если в датасете содержатся длинные тексты, но с большим количеством повторяющегося контента (типовые правовые договоры или медицинские выписки, где важные детали добавляются в общий шаблон), то более низкое значение N может работать эффективнее.

С другой стороны, если в датасете много текстов, отличающихся в первую очередь порядком слов, то более высокое значение N может подойти лучше, так как будет к нему более чувствительно.

Меняем в предыдущем коде параметр N с 3 на 10 и смотрим, как изменился результат:

print(jaccard(message, message))
# 1.0

print(jaccard(message, permuted_message))
# 0.4074074074074074 (vs. ~0.79)

print(jaccard(message, similar_message))
# 0.23076923076923078 (vs. ~0.37)

print(jaccard(message, different_message))
# 0.0 (vs. ~0.02)

Поэтому проще всего поэкспериментировать с небольшой частью данных и разными значениями N и выбрать наиболее подходящий вариант.

Как ещё можно искать близкие тексты?

Другие метрики близости между текстами (edit distance metrics), которые часто используются в компьютерной лингвистике и биоинформатике:

• Расстояние Левенштейна — метрика, для которой считается минимальное количество односимвольных операций (вставка, удаление, замена символа), которые нужны для того, чтобы превратить одну строку в другую.

• Расстояние Дамерау-Левештейна — к операциям, определенных в метрике расстояния Левенштейна, добавляется ещё операция транспозиции (перестановка соседних символов).
  
  Обе метрики опираются на алгоритм динамического программирования Вагнера-Фишера.

• LCS (наибольшая общая подпоследовательность) — решается задача поиска всех наибольших подпоследовательностей. Используется, например, в утилите diff.
  Внимание: подпоследовательность != подстроке. Например, вла является только подпоследовательностью слова вилка, а вил — и подпоследовательностью, и подстрокой.

• Расстояние Хэмминга — использует только операции перестановки. Этот алгоритм работает подходит дли последовательностей одной длины.

Реализацию на Питоне можно найти, например, в пакете pyeditdistance или соответствующем модуле NLTK.

Поиск текстов, близких по смыслу

Для того, чтобы найти тексты, близкие друг другу не только на уровне похожести строк, но и по смыслу, можно использовать векторные представления текста.

Идея следующая:

• кодируем текст при помощи понравившейся модели (word2vec, fastText или Sentence Transformers, например, LABSE);

• вычисляем близость между получившимися векторами при помощи, например, косинусной меры сходства;

• ранжируем тексты по схожести и, в зависимости от задачи, определяем подходящий порог, после которого данные будут отфильтровываться;

• удаляем слишком близкие друг к другу тексты.

По моему опыту, для многих задач именно на этапе фильтра датасета такой подход уже становится overkill'ом. Во-первых, часто тексты с близким по смыслу значением, выраженным по-разному, как раз интересны для разработки модели (нужно много перефразированных вариантов одного и того же интента для чат-бота, например). Во-вторых, качество ранжирования упирается в качество самих векторных представлений. Но в любом случае полезно знать, что можно попробовать очистить данные ещё и так.

Работа с большими данными: LSH, MinHash

Если датасет достаточно большой, то может быть сложно построить попарную матрицу расстояний между текстами за разумное время.

Например, есть датасет из миллиона текстов реплик в чатах, из которых нужно удалить похожие.

Для того, чтобы попарно сравнить все текстов, необходимо сделатьсравнений. Соответственно, для нужно будет сравнить тексты раз.

Допустим, мы сравниванем тексты попарно со скоростью миллион в секунду. В одних сутках 86400 секунд. Это значит, что для обработки датасета из миллиона записей понадобится почти 6 дней.

Даже если 6 дней вычислений нас в целом устраивают, такой способ поиска дубликатов плохо масштабируется: как только алгоритм поиска близости усложнится или данных станет существенно больше, время на обработку может в разы увеличится.

Избежать долгих вычислений можно, если вместо попарного сравнения решать задачу приближенного поиска ближайших соседей (ANN).

Идея такая: чтобы сократить количество вычислений, нужно сократить число возможных сравнений. Это можно сделать, если сравнивать вектор текста не с векторами всех остальных текстов из датасета, а ограничить количество кандидатов только теми, которые мы предположительно считаем возможными дубликатами.

Найти таких наиболее вероятных кандидатов можно при помощи Locality-Sensitive Hashing (LSH), одного из наиболее популярных алгоритмом для задачи ANN. Это вероятностный метод снижения размерности, при котором подбираются такие хэш-функции (функция, которая преобразует объекты в битовые последовательности одинаковой длины), чтобы похожие тексты с высокой вероятностью попадали в одну "корзину" (buckets).

Поскольку длина битовой последовательности, в которую хэш-функция преобразует объекты, ограничена, могут возникать коллизии. Коллизия означает, что разные объекты преобразуются в одну и ту же хэш-сумму.

В обычной ситуации цель при использовании хэш-функций — минимизировать количество коллизий.

Например, мы хэшируем пароли пользователей и храним в базе данных только хэш-суммы. Хакер получил доступ к базе данных, но не находит там оригинальных паролей пользователей, поэтому на первый взгляд кажется, что все в порядке. Но если при хэшировании паролей использовалась функция, коллизии для которой можно найти гораздо быстрее, чем простым перебором, то существует высокая вероятность, что хакер сможет подобрать другой пароль с той же хэш-суммой, что и пароль от личного кабинета пользователя, и воспользоваться им.

Поэтому для хэширования ключей в словаре Python, паролей или электронных подписей большое количество коллизий — недостаток. Но не для поиска дубликатов.

Хэш-функции для LSH, наоборот, максимизируют количество коллизий. В отличие от ситуации с паролями, если похожие друг на друга тексты получится положить в одну и ту же ячейку, то мы только выиграем.

Эти функции чувствительны к местоположению (locality sensitive), из-за чего в одну и ту же ячейку помещаются не случайные объекты, а близкие друг к другу точки. Это позволяет сравнивать текст не со всеми остальными данными, а только с подмножеством наиболее близких текстов, попавших с ним в одну корзину.

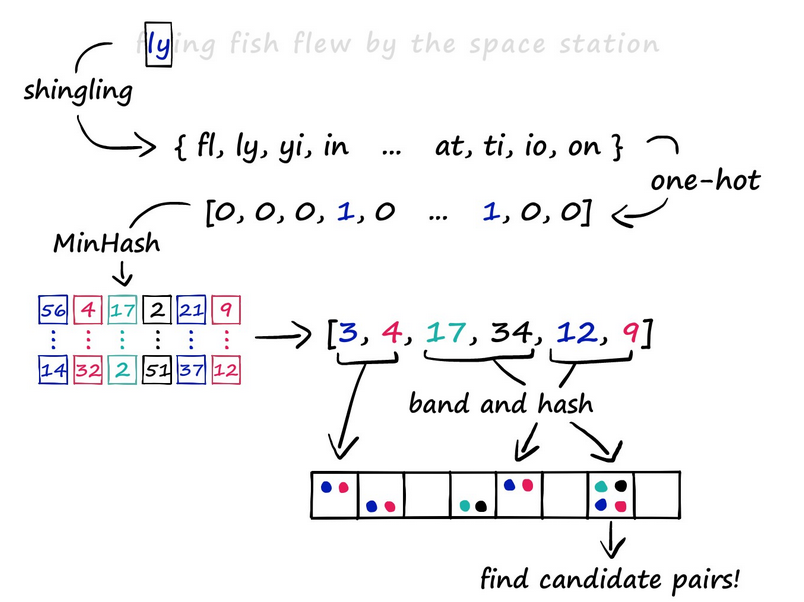
Методов LSH много, но основная идея для всех: при помощи хэш-функций сложить похожие объекты в одни и те же ячейки.

Вот из каких этапов состоит классический подход:

• Shingling: уже описанное выше разделение текста на n-граммы;

• One-hot-encoding: преобразуем полученные n-граммы, получаем векторы для текстов;

• MinHash —  алгоритм, который позволяет находить похожие множества эффективнее, чем мера близости Жаккара, с помощью хэш-функций.
  В данном случае мы используем его для того, чтобы преобразовать векторы в сигнатуры меньшей размерности, которые при этом с некоторой вероятностью всё ещё позволяют оценить их сходство.

• LSH: сигнатуры, полученные на предыдущем этапе, разбиваем на b частей, а потом раскидываем на k корзин (последний этап на схеме выше). Сигнатуры, части которых хотя бы раз попали в одну и ту же корзину, считаем кандидатами в дубликаты.

• Ищем дубликаты, сравнивая тексты друг с другом только внутри одной корзины.

Подробнее почитать про LSH в простом изложении и с кодом можно в посте James Briggs (иллюстрация выше как раз из него) и cтатье Matti Lyra.

Если хочется чего-то более фундаментального, то тема поиска дубликатов, на мой взгляд, лучше всего раскрывается в 3 главе классической книги Mining of Massive Datasets (книга, видео).

А реализации, помимо больших фреймворков для бигдаты, есть, например, здесь:

• имплементация SimHash от scrapinghub

• фреймворк NearPy

• пакет datasketch

На этом всё. Надеюсь, что эти советы по удалению дубликатов будут вам полезны. Делитесь своими лайфхаками в комментариях: какие подходы обычно используете и на каких данных, что хорошо работает, а что практически не меняет картину? И не забывайте лайкать пост ????