Разбираем особенности алгоритмов CatBoost и LightGBM: какой от них профит / forpes.ru

Главная
Разбираем особенности алгоритмов CatBoost и LightGBM: какой от них профит

Разбираем особенности алгоритмов CatBoost и LightGBM: какой от них профит +13

28.07.2023 13:22

artur_sosnovikov 0 1700 Источник

Всем привет. Меня зовут Артур. Я тимлид ДС команды в компании Точка. Сегодня расскажу вам про особенности алгоритмов CatBoost и LightGBM. Для чего они нужны, в чём их фишки и как они облегчают нам работу с данными.

Почему я решил написать эту небольшую статью. Готовясь к выступлению на внутреннем митапе по теме особенности алгоритмов у CatBoost и LightGBM, я понял, что не смог найти единого места, где были бы понятным языком рассказаны основные особенности того, что алгоритмически работает под капотом у CatBoost и LightGBM. Причём не формальные записи алгоритмов на псевдокоде, а понятные пошаговые инструкции.

Мы будем по возможности избегать излишней формализации, чтобы понятным языком изложить смысл.

Кому будет полезно

Начинающим, а также тем, кто продолжает свой путь в машинном обучении и уже имеет представление, как работает классический градиентный бустинг, понимает, как строятся бинарные деревья решений. Первая по-настоящему крутая и популярная в народе реализация бустинга — XGBoost (о ней как раз много написано везде, поэтому не разбираем его в этой статье), при этом, когда говорим об особенностях, нередко имеем в виду улучшение над XGBoost.

Не менее полезно спецам DS до уровня middle+ для расширения кругозора (когда часто используешь библиотеку, но не было времени вникнуть, как там что конкретно работает).

И разумеется тем, кто готовится к собесам и хочет произвести хорошее впечатление. Одного рассказа про EFB, думаю, будет достаточно. На внутренних грейдированиях я впечатлялся, если кто-то перечислял хотя бы некоторые особенности.

Классический вариант градиентного бустинга

Чтобы лучше понять разницу между библиотеками, давайте вспомним, как вообще ставится задача для классического градиентного бустинга.

Дисклеймер:

если вы всё это помните, переходите к следующему разделу про CatBoost, а если наоборот хотите разобраться в этом поглубже, рекомендую вот этот материал от Академии Яндекса

Пусть мы имеем:
— объект из обучающей выборки
— объектов в обучающей выборке
— наш алгоритм, представляющий собой линейную комбинацию базовых алгоритмов
(во всех “стандартных” реализациях — решающие деревья из семейства

— гладкая функция потерь

Ставится задача минимизировать «эмпирический риск»

$\sum_{i=1}^{N}{\mathcal{L}(y_i, a(x_i))}$

Представим наш алгоритм как $a_k(x) = a_{k-1}(x) + b_k(x)$ , где

$a_{k-1}(x) - текущее\ приближение;\\b_k(x) - следующие\ приближения$

Как-то инициализируем первое приближение (для этого придумано много разных эвристик)
Дальше на шагеалгоритм подбирается так, чтобы минимизировать эмпирический риск:

$b_k = \underset{b \in B}{\arg\min} \sum_{i=1}^{N}{\mathcal{L}(y_i, a_{k-1}(x_i) + b(x_i))}$

Разложим функцию потерь $\mathcal{L}$ до первого члена в окрестности точки $(y_i, a_{k-1}(x_i))$

$\mathcal{L}(y_i, a_{k-1}(x_i) + b(x_i)) \approx \mathcal{L}(y_i, a_{k-1}(x_i)) + b(x_i)\frac{\partial\mathcal{L}(y_i, z)}{\partial z}\bigg|_{z=a_{k-1}(x_i)} =$ $= \mathcal{L}(y_i, a_{k-1}(x_i)) + b(x_i)g_i^{k-1}$

Считаем при этом, чтодостаточно малы, чтобы такое разложение оставалось приближенно верным. Первый член на этом шаге постоянный, поэтому получается такая оптимизационная задача:

$b_k \approx \underset{b \in B}{\arg\min} \sum_{i=1}^{N}{b(x_i)g_i^{k-1}}$

Т.е. минимизируем скалярное произведение векторов: («вектор ответов алгоритма на объектах обучающей выборки», «вектор градиентов функции потерь, вычисленных на ответах алгоритма на предыдущем шаге»).

Минимум скалярного произведения достигается, если вектор противоположен вектору $g_i^{k-1}$ , т.е $b(x_i) = - g_i^{k-1}$ Поэтому на каждой итерации базовые алгоритмы обучаются предсказывать значения антиградиента функции потерь на предсказаниях алгоритма $a_{k-1}(x_i)$ на предыдущем шаге.

Обучение базового алгоритма

При построении очередного базового алгоритма $b_{k}$ мы решаем задачу регрессии с таргетом, равным антиградиенту функции потерь исходной задачи на предсказании $a_k = b_1+\ ...\ +b_{k-1})$

Теоретически можно воспользоваться любым методом построения регрессионного дерева. Важно выбрать оценочную функцию , которая будет показывать, насколько текущая структура дерева хорошо приближает антиградиент. Её нужно будет использовать для построения критерия ветвления

$| R | \cdot S(R) - |R_{right}| \cdot S(R_{right}) - |R_{left}| \cdot S(R_{left}) \rightarrow \max,$

где — значение функции в вершине , $S(R_{left})$ , $S(R_{right})$ - значения в левых и правых сыновьях после добавления предиката, $|\cdot|$ — количество элементов, пришедших в вершину.

Например, можно использовать следующие оценочные функции:

$L_2(g,p)=\sum_{i=1}^N{(p_i-g_i)}^2, Cosine(g,p) = -\frac{\sum_{i=1}^N{(p_i \cdot g_i)}}{\sqrt{\sum_{i=1}^N{p_i^2}}\cdot \sqrt{\sum_{i=1}^N{g_i^2}}}$

где - предсказание дерева на объекте , - антиградиент, на который учится дерево, $p = \{p_i\}_{i=1}^N$ , $g = \{g_i\}_{i=1}^N$ . Функция представляет собой среднеквадратичную ошибку, а функция определяет близость через косинусное расстояние между векторами предсказаний и антгирадиентов.

Замечу, что почти всегда выбирается оценочная функция чтобы задача сводилась к привычному всем методу наименьших квадратов. Однако в catBoost'е используется косинусное расстояние.

Перейдем к CatBoost

Мы все любим CatBoost, пользуемся и уважаем его. И есть за что. CatBoost, как правило, хорошо работает уже «из коробки» без утомительной настройки гиперпараметров. Указал адекватные значения темпа обучения, подал список категориалок и можно запускать.
Если копнуть чуть глубже, под капотом решаются ещё и «классические» проблемы всех бустингов. Это проблемы, связанные с утечкой информации из зависимой переменной. Чтобы решить эти задачи, было сделано несколько вещей:

Симметричные забывчивые деревья
Обработка категориальных признаков
Динамический бустинг

Симметричные забывчивые деревья

Забывчивые деревья, они же решающие таблицы. Чем они хороши.

Значительное ускорение производительности по сравнению со стандартным послойным построением деревьев. Как при обучении, так и при инференсе
Уменьшение переобучения
Устойчивость к изменению гиперпараметров

Ниже пример симметричного забывчивого дерева. В каждом узле на одном и том же уровне дерева используется одна и та же точка расщепления.

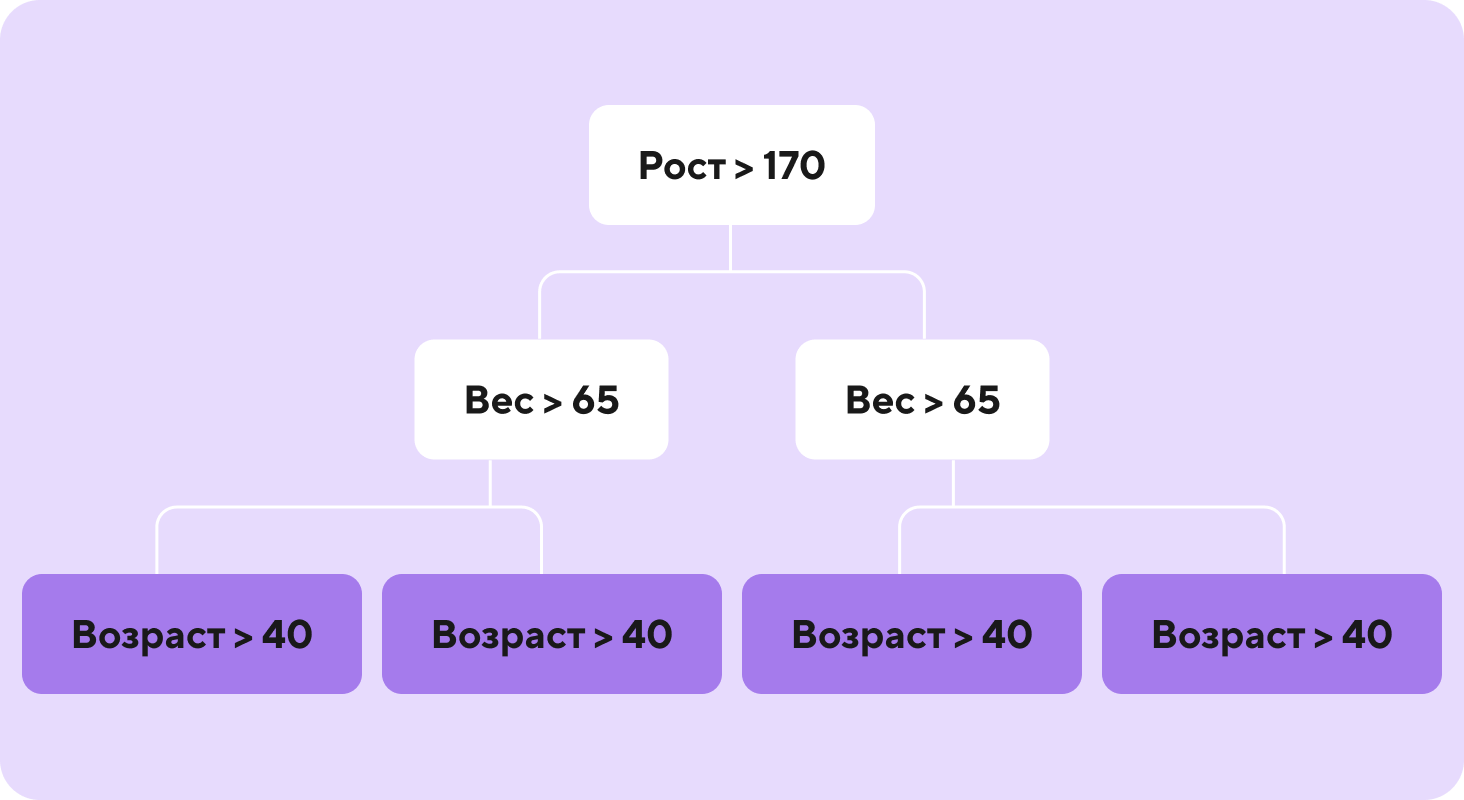
Добавлю, что в CatBoost кроме симметричных забывчивых деревьев (используется по умолчанию, growpolicy=’SymmetricTree’) можно строить деревья принципиально похожие на деревья LightGBM (строятся повершинно, пока не будет достигнуто заданное количество лисьтев, growpolicy= Lossguide’) и XGBoost (строятся слой за слоем, пока не будет достигнута заданная глубина, growpolicy= ‘Depthwise’).

Теперь поговорим про категориальные признаки

Что можно сделать с признаками? Разберём на примере задачи бинарной классификации.

Представим, что у нас есть табличка.

Есть простые способы:

Просто перенумеровать признаки.
1. Пример. Признак «Домашний Питомец» имеет значения: Котик, Пёсель, Хомяк и т.д.) от 0 до N (label encoding). Котик — 0, Пёсель — 1 и тд.
2. Проблема. Одна из проблем состоит в том, что устанавливается порядок (которого в нашем примере нет) между значениями признака. Пёсель (1) > Котик (0)
One-hot encoding.
1. Пример. Превращаем нашу табличку в такую, как показано ниже. Т.е. заменяем один категориальный признак на N бинарных признаков.
2. Проблема. Хорошо работает, только если значений у признака мало.

Есть более сложные способы (на статистиках по категориальным признакам).

Заменять категориальный признак на среднее значение метки класса (простой mean target encoding).

Пример. Котик в нашей выборке встречается 3 раза. Метка класса равна 1 два раза. Заменяем Котика на 2/3. В табличке ниже для наглядности оставим значения в виде обыкновенной дроби.

Проблемы. При этом способе кодировки возникают две проблемы с переобучением.

Явная проблема — Хомяк. Встретился всего один раз и его заменили просто на значение таргета. Очевидно, что на тестовой выборке такой связи, в общем случае, не будет.
Менее явная проблема. При такой кодировке в каждой строке мы фактически использовали «мини модель». При этом для каждой строки мы использовали все наблюдения, включая текущее. Что, в сущности, является утечкой.

Как сделано в CatBoost

В CatBoost реализован модифицированный подход к mean target encoding.

Кодировка состоит из двух этапов (происходит на каждой итерации построения очередного дерева):

Случайная перестановка.
Статистика «по прошлому». Для текущей строки после случайной перестановки считаем среднее значение таргета при этом уровне признака, вычисленное по предыдущим строкам.

В формуле для кодировки используются следующие значения.

#positive – количество единичек в «метке класса», встретившихся до текущей записи;
#All — количество наблюдений данного класса, встретившихся до текущей записи;
Prior — просто небольшое число.

Покажем вычисления (Prior = 0.01 - этот параметр можно подбирать на примере наблюдения с Id == 2. До этого наблюдения в классе «Котик» встретилось два наблюдения, поэтому #All = 2. У этих двух наблюдений «метка класса» == 1 в одном наблюдении (id == 1)

Комбинации. Также используются комбинации категориальных фичей. Это отличная фишка алгоритма. Так как на этапе предобработки, в общем случае, не получится построить все комбинации категориальных фичей — количество комбинаций будет расти экспоненциально.

В катбусте комбинации катфичей строятся не перед началом обучения, а жадным алгоритмом при построении каждого дерева. Приведу пример. Пусть у нас есть категориальные признаки x1, x2, x3, x4. Если был выбран для сплита на некотором уровне категориальный признак x1, то на следующем уровне дерева будут перебираться такие комбинации: признаки сами по себе (x1, …, x4) и комбинации только с выбранным ранее признаком (x1+x2, x1+x3, x1+x4). Предположим теперь, что для разбиения на этом уровне была выбрана комбинация x1+x4. На следующем за ним уровне будут опять перебираться признаки сами по себе(x1, …, x4), двойные комбинации с первым отобранным категориальным признаком (x1+x2, x1+x3, x1+x4) и тройные комбинации с отобранной ранее парой признаков ([x1+x4] + x2, [x1+x4] + x3). И так далее. Такой алгоритм помогает найти удачные комбинации признаков при этом не перебирая экспоненциально большое количество комбинаций.

One-hot encoding. Кстати, кроме описанного выше алгоритма, в CatBoost также реализован классический One-hot encoding. Условия применения регулируются гиперпараметром one_hot_max_size. По умолчанию, за некоторым исключением, такая кодировка используется для фичей с 2 различными значениями.

Динамический бустинг: ещё одно нововведение CatBoost

Как происходит обычно: Для данного наблюдения оценка градиента — средний градиент по всем объектам в листе (с точностью до регуляризяции и т.д.). Выходит, что для каждого конкретного наблюдения используется его таргет для вычисления градиента, т.е. невольно подглядываем в таргет и это приводит к переобучению. Особенно чувствительно это на маленьких обучающих выборках.

Нововведение CatBoost — при вычислении градиента используется идея, похожая на ту, что описана в части про обработку категориальных признаков. А именно:

Делаются случайные простановки.
Для данного объекта значения в листе считаются по наблюдениям, которые появились в листе раньше. В лоб такая схема имеет квадратичную сложность. В CatBoost реализовано уменьшение сложности алгоритма.

Отмечу, что такая схема показывает эффективность на «маленьких» обучающих выборках. На больших выборках такой подход не особо нужен. Поэтому в CatBoost под капотом по размеру датасета выбирается, будет ли при обучение использован описанный выше подход с упорядочиванием или будет использован классический подход.

Разбираем особенности LightGBM

LGBM появился (официально) немного раньше, чем CatBoost. В нём есть свои особенности, но главная — он ультрабыстрый и нетребовательный к ресурсам.

Как рассуждали авторы исследования алгоритма LGBM, слабое место со скоростью у классического градиентного бустинга состоит в том, что при построении каждого дерева приходится оценивать информационный выигрыш для всех возможных точек расщепления. То есть, проводить вычисления для каждого признака и для каждого наблюдения. Сложность получается O(m-наблюдений х k-признаков).

Соответственно, чтобы ускорить вычисления, нужно сделать следующее: строить деревья быстрее за счёт другой структуры, уменьшить количество наблюдений, уменьшить количество признаков. И при этом нужно постараться не сильно потерять в точности.

Таким образом становится понятно, зачем в LGBM применили эти приёмы:

Повершинное построение деревьев — ускорение за счёт структуры.
GOSS (Gradient-based One-Side Sampling). Используем меньше наблюдений.
EFB (Exclusive Feature Bunding). Используем меньше признаков.

Заметка. Уменьшение количества признаков за счёт гистограммирования оставим за скобками, т.к. оно используется во всех трёх классических библиотеках.

Пойдём по порядку.

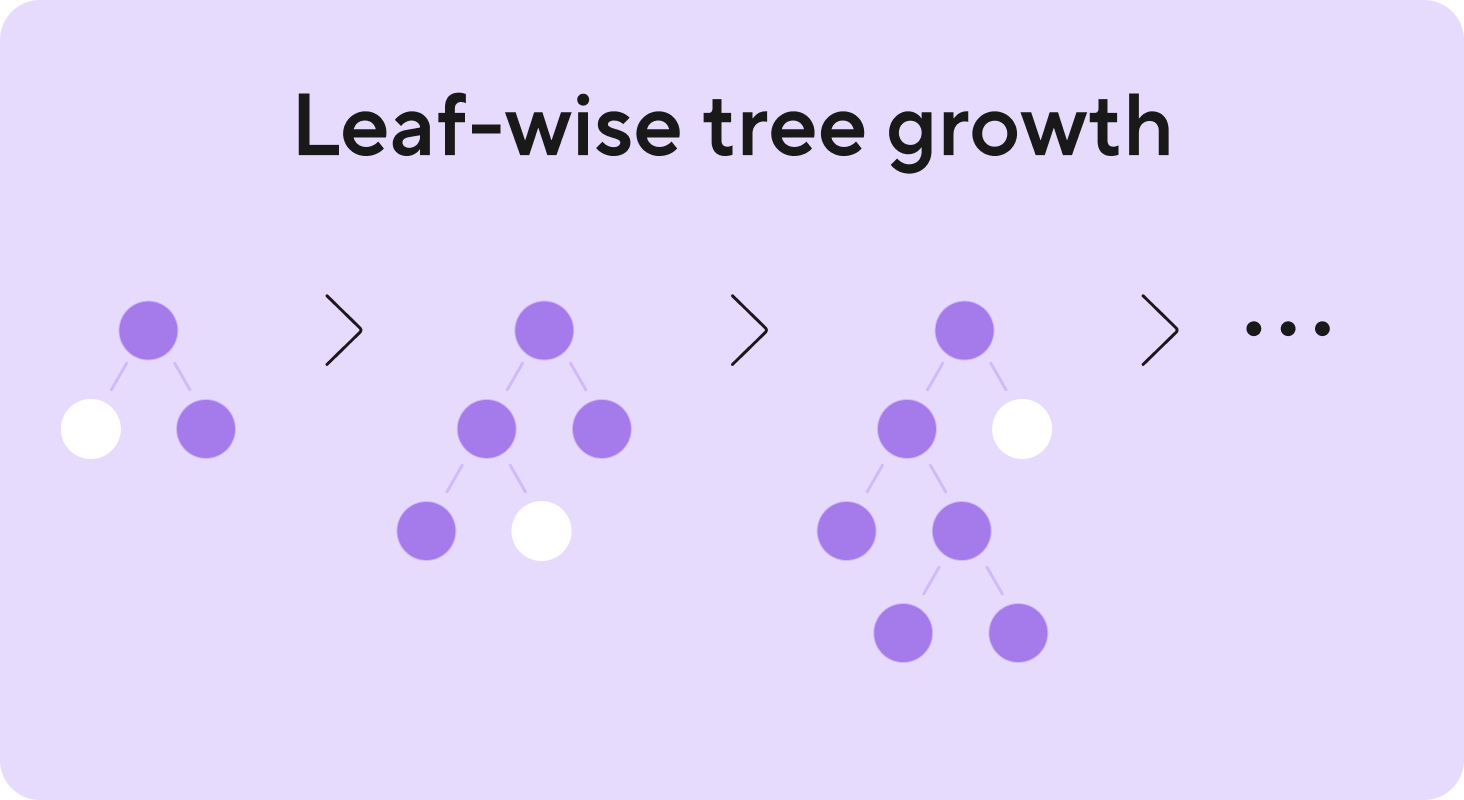
Повершинное построение деревьев (Leaf-wise tree growth)

В начале статьи уже упоминался этот алгоритм. Остановимся теперь на нём подробнее. Мы строим деревья не слой за слоем, а выбираем лист в котором уменьшается наш loss сильнее, чем в остальных. Этот лист дальше разбиваем, растим, и получается, что у нас деревья могут быть несимметричные и глубокие. Этот алгоритм (Friedman et al., 2000) значительно быстрее, чем классические алгоритмы (типа CART (Breiman et al., 1984) или C4.5 (Quinlan, 1993)) построения слой за слоем.

GOSS

Переводится как односторонний отбор на основе градиентов. В чём фишка: у вас есть некоторые наблюдения, в которых градиент большой. Обычно таргет на них хуже предсказывается (т.е. больший потенциал для улучшения качества модели), чем на наблюдениях, где градиент маленький. Хотелось бы, обучаясь, обратить большее внимание на эти наблюдения, чем на наблюдения с маленьким градиентом.

Т.к. для минимизации этого скалярного произведения $b_k \approx \underset{b \in B}{\arg\min} \sum_{i=1}^{N}{b(x_i)g_i^{k-1}}$

очевидно лучше подобрать базовый алгоритм так, чтобы на объектах, где градиент $g_i^{k-1}$ максимален. Ответы базового алгоритма были $b(x_i) = -g_i^{k-1}$ Таким образом самые «весомые» слагаемые будут сделаны минимальными, а небольшие слагаемые — погоду особо не делают.

Работает это всё следующим образом. Вы берёте наблюдение с большим градиентом, выбираете какую-то долю (для примера я назвал a таких наблюдений). Теперь у вас есть все оставшиеся наблюдения. Из неё вы делаете подвыборку, и берёте какую-то долю из оставшихся наблюдений. Далее веса для таких наблюдений вы усиливаете множителем . Это сделано для того, чтобы не перекособочить реальное распределение данных.

Односторонний отбор на основе градиентов

В итоге мы получаем значительный буст скорости. Мы обрабатываем не все наблюдения, а имеем дело с небольшой частью, и при этом уделяем особое внимание тем наблюдениям, где градиенты самые большие.

EFB

Связка взаимоисключающих признаков. Идея такая: вместо k-признаков, построить p-связок и использовать только их при нахождении оптимальной точки расщепления при построении деревьев. Причём построим эти связки только один раз — в самом начале. Сложность этого действия .

Решаем две задачи:

Какие признаки связывать.
Как конструировать связку, когда выбрали признаки, которые хотим связать.

Какие признаки связать

Введём некоторые несложные определения. Взаимоисключающие признаки — никогда не принимают одновременно ненулевое значение (например, для понимания, при кодировании категориалок методом One-hot encoding получаем взаимоисключающие признаки (см. картинку выше)

Разумеется, в общем случае, в реальных данных так почти никогда не бывает, чтобы признаки были строго взаимоисключающие. Поэтому вводится «количество конфликтов» между двумя признаками — количество наблюдений где два признака принимают одновременно ненулевые значения. Можно ввести долю конфликтов, при которой признаки допустимо объединять в связки.

Задача связки признаков можно переформулировать как классическую задачу раскраски графа с помощью жадного алгоритма. Покажу пример:

Пусть у нас есть данные.

Светлым выделены конфликты признаков х1 и х2,Темным - х2 и х3 — Светлым выделены конфликты признаков х1 и х2,
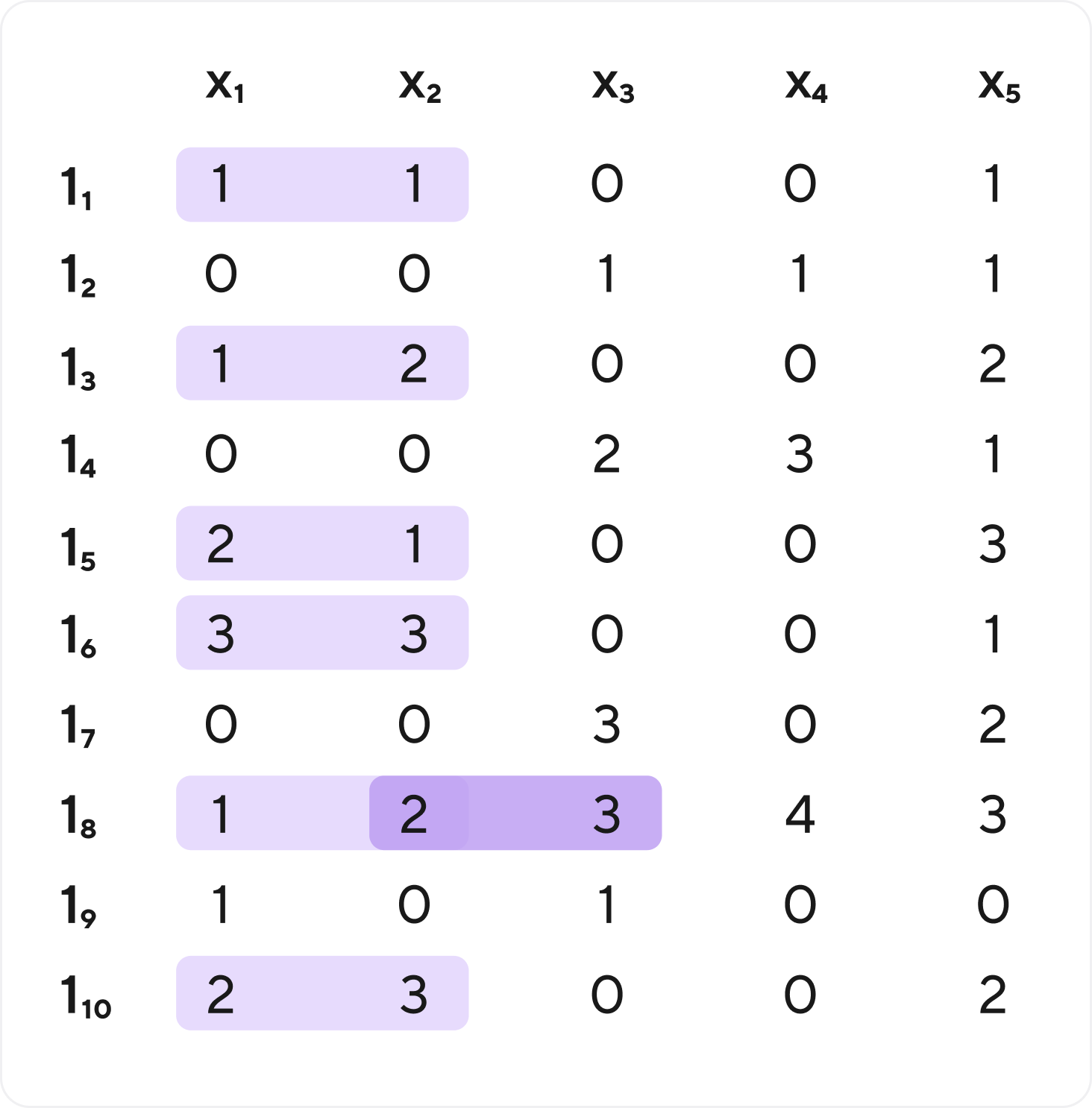
Темным - х2 и х3

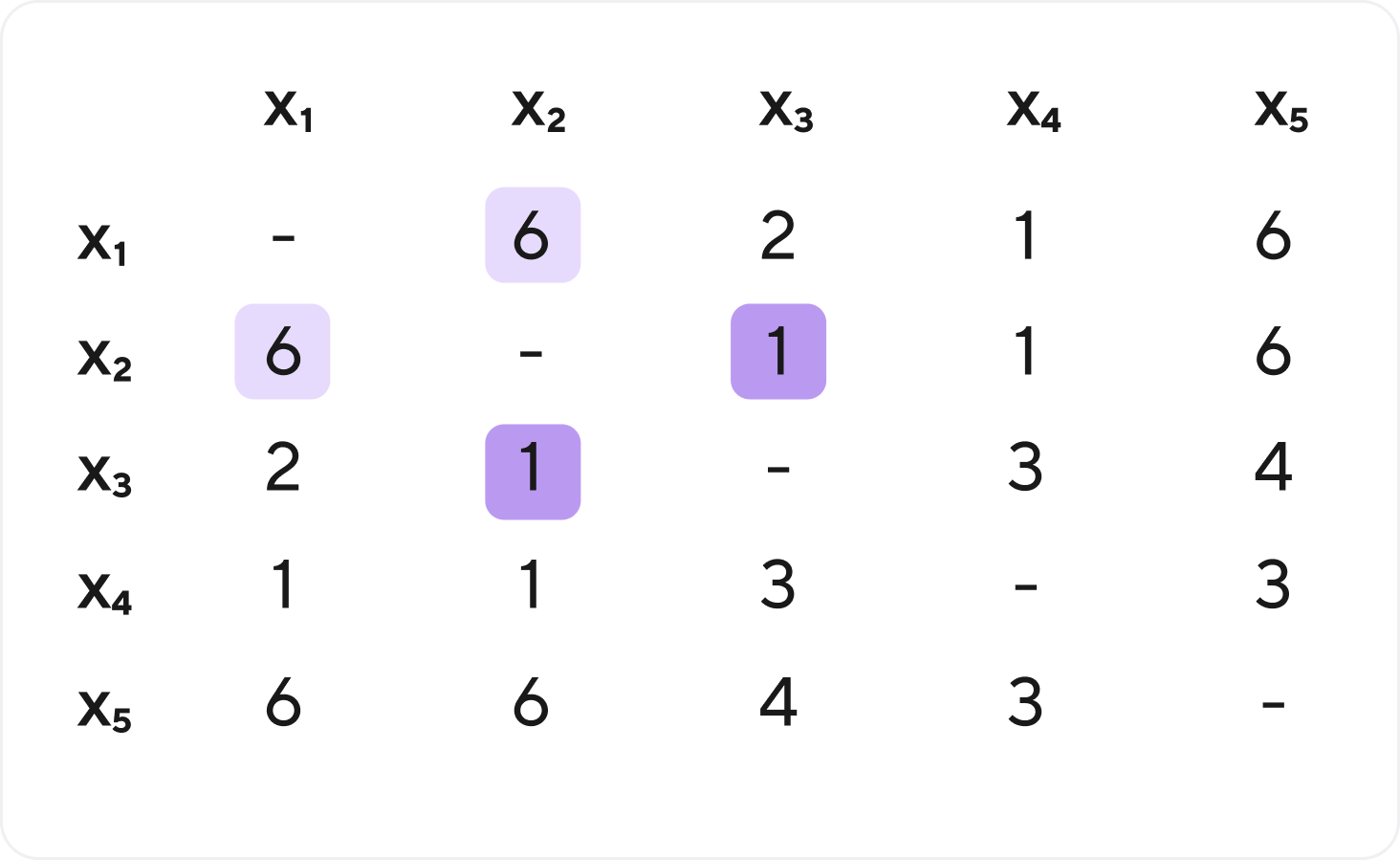
Составим матрицу конфликтов между признаками. Светлое к светлому, темное к темному.

Упорядочим признаки по степени — сумма значений признака по всем наблюдениям.

Построим граф. В вершинах признаки, все признаки связаны попарно, а веса рёбер — количество конфликтов. Выберем допустимую долю конфликта между признаками (например 0.2). Т.к. в нашем примере 10 наблюдений, то в абсолютных величинах — это 2 конфликта.

Начнём с признака с x5 (самая высокая степень) и отрежем рёбра где конфликтов больше 2.

Получается, отрезали все рёбра. Признак х5 изолировался.

Теперь берём следующий признак по степени — х1 и отрезаем рёбра с высоким конфликтом. Остаётся х4.

Теперь признак х4. Он не конфликтует с х2, но его нельзя взять в связку из-за конфликта (х1-х2). Получается связка х1-х4Т.

И остается связка х2-х3.

Таким образом вместо 5 признаков получили 3 связки.

Как конструировать связку, когда выбрали признаки, которые хотим связать

Смотрим на связку х2-х3 и конструируем признак х23. Максимальное значение этого признака — 3.

Там где он не ноль, а признак х3 ноль, там у х23 значение как у х2. (строчка 1) Когда наоборот, то к значению признака х3 добавляем число 3 (то самое максимальное значение признака х2). строчка 2

Конфликт выделен красным — там опять же значение как у х2 строчка 8

Подводя итоги

Мы узнали как под капотом устроены библиотеки CatBoost и LightGBM. Поняли почему в CatBoost не надо запариваться с настройкой гиперпараметров — из коробки всё хорошо. Не надо перекодировать фичи — CatBoost сделает это прекрасно сам. LightGBM — быстрый, требует мало ресурсов, но при этом нет особой потери в качестве.

По личному опыту могу сказать, что если нужно быстро построить бейзлайн решения и ресурсов достаточно, CatBoost отлично для этого подойдёт (зачастую при построении бейзлайна достаточно указать только количество деревьев и не надо даже темп обучения подбирать, т.к. подбирается автоматически, используя эвристики). Нередко, как, например, в развёрнутой нами в Точке модели оттока клиентов, CatBoost становится продовым решением, т.к. получается высокое качество модели и высокая скорость предсказаний.

LightGBM — отлично справляется с задачами. Особенно полезен, когда есть ограничения по ресурсам. Учится весьма быстро. Однако требуется определённая сноровка, чтобы правильно стартовать обучение с адекватными гиперпараметрами.

Есть множество сравнений этих библиотек. Как правило, они показывают примерно одинаковое качество на различных задачах.

Что ж, обсудили основные детали библиотек CatBoost и LightGBM. Теперь можем использовать их более осмысленно (и поражать воображение интервьюеров на собеседованиях).

Для тех, кто хочет дойти до самой сути — дополнительные ссылки:

Классическая статья про градиентный бустинг от самого автора и еще одна от него же

Ссылка на википедию про бустинг

Статья про XGBoost

Хорошее пошаговое описание как устроен градиентный бустинг от Бэна Гормана

Классическая статья по катбусту

Классическая статья по LightGBM

Про решающие таблицы в катбуст